Advances in Applied Mathematics
Vol.
12
No.
04
(
2023
), Article ID:
64874
,
15
pages
10.12677/AAM.2023.124206
(3 + 1)维幂律3 Zakharov-Kuznetsov方程的 行波解
——兼论幂律n
王双特1,于恒国2,刘环艺2,戴文周1
1乐清市柳市镇第三中学,浙江 温州
2温州大学数理学院,浙江 温州
收稿日期:2023年3月26日;录用日期:2023年4月21日;发布日期:2023年4月29日

摘要
借助于平面动力系统理论,定性分析了非线性(3 + 1)维幂律3 Zakharov-Kuznetsov方程的行波解,同时给出了行波解的分类及近似解计算方法。结合相关文献,整体上讨论了幂律为n时Zakharov-Kuznetsov方程的行波解,由此推广了本文及相应文献中的结果。
关键词
Zakharov-Kuznetsov方程,平衡点,行波解,幂律

Travelling Wave Solutions of a (3 + 1) Dimensional Zakharov-Kuznetsov Equation with Power Law 3
—On Power Law n
Shuangte Wang1, Hengguo Yu2, Huanyi Liu2, Wenzhou Dai1
1Yueqing Liushi No.3 Middle School, Wenzhou Zhejiang
2College of Mathematics and Physics, Wenzhou University, Wenzhou Zhejiang
Received: Mar. 26th, 2023; accepted: Apr. 21st, 2023; published: Apr. 29th, 2023

ABSTRACT
With the aid of the theory of planar dynamical system, it has qualitatively analysis travelling wave solutions of a nonlinear (3 + 1) dimensional Zakharov-Kuznetsov equation with power law 3. The classification and approximate calculation methods of travelling wave solutions are also derived. Combining corresponding literature, in general, travelling wave solutions the of Zakharov-Kuz- netsov equation with power law n are discussed. Therefore, it extends outcomes in this paper and corresponding literature.
Keywords:Zakharov-Kuznetsov Equation, Equilibrium, Travelling Wave Solution, Power Law

Copyright © 2023 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
众所周知,(2 + 1)维Zakharov-Kuznetsov方程(ZK方程)
(1)
是KdV方程在二维空间的推广形式,它是应用渐进多尺度技术在磁场中发现的一种磁等离子波,在物理学领域有着广泛的应用 [1] ,许多学者对其进行了广泛的研究 [2] - [16] 。一般的,具有幂律 非线性(3 + 1)维Zakharov-Kuznetsov方程 [6] [7] [16] 为
, (2)
其中 是非零常数, 是Laplace算子, 。受文 [6] [7] [10] [11] [12] [16] 的启发,本文重点考虑幂律3 ZK方程的行波解,整体安排如下。首先,给出相应常微分系统的平衡点情况,如个数和类型;其次,针对行波解的分类及形式进行了讨论,同时给出其近似解的计算方法,基于此,在形式上给出了ZK方程对称的一种表达式;最后,对幂律 为正整数时的ZK方程作初步定性分析。
2. 准备工作
对于幂律为3的ZK方程
, (3)
作行波变换 , , 为波速,积分一次后化为二阶常微分方程(ODE)
, (4)
其中 是积分常数,上标’(撇)指对 求导,下同。为简便,设 和 ,上述ODE化为常微分系统
。 (5)
显然首次积分为 ,所定义的轨线为 。注意,如果设首次积分形式为 , 为关于 的多项式,由交换代数理论的除法定理 [17] [18] 知,存在复数域上多项式 ,使得 ,再取 ,比较系数有 , , , 。计算得 为非零常数, ,而 ,又回到上述形式。
当 时,系统(5)的平衡点为 和 。当 时, 为鞍点,由对称原理 [19] 知 为中心;当 时, 为中心,而 为鞍点。而轨线经过点 和点 时临界值分别为 和 , 与 同号。图1给出了 时四种轨线图。
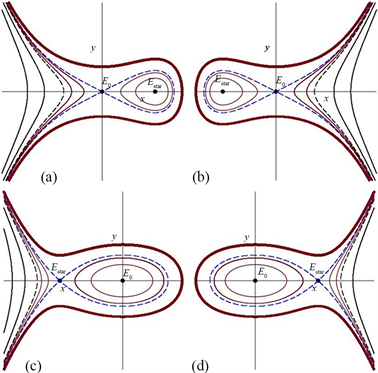
Figure 1. Trajectories with : (a) ; (b) ; (c) ; (d)
图1. 时轨线:(a) ;(b) ;(c) ;(d)
3. 时的行波解分支
3.1. 平衡点的个数
引入四次方程 的判别式 , , , ,分为三种情形进行考虑:情形1. 或 ,此时方程有一对二重实根和一对共轭复根,即仅有一个平衡点;情形2. 或 ,此时方程有两个不等实根和一对共轭复根,即有两个平衡点;情形3. 或 ,此时方程有两对不等的共轭复根,即没有平衡点。
如果改写方程 为 ,则实根情况转化为两个函数 和直线 的交点情况。显然,当 ( )时函数 有最大(小)值 。以 为例,当 , 和 时,分别对应0个,1个和2个交点,即又回到了上述三种情形。类似的,可以说明 时的三种情形。图2说明了以上分析。
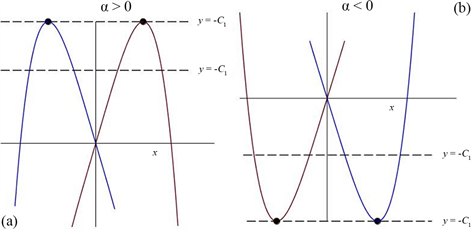
Figure 2. The figures of functions and : (a) ; (b)
图2. 函数 与直线 的图象:(a) ;(b)
3.2. 情形1: 或
此时唯一的平衡点 为高阶奇点,因Jacobi矩阵 的行列式和迹均为零。取变换 , 和 , , , ,化为系统
, 。 (6)
这等价于系统 , ,因此 是余维至少为4的尖点 [20] 。轨线经过该奇点的临界值为 , 与c同号。表1说明了参数间关系,+﹑−分别表示大于﹑小于零(下同)。
Table 1. Relationship of parameters with α = α 0 ( Δ x = 0 )
表1. ( )时参数间关系
图3则给出了 ( )时的四种轨线图。
3.3. 情形2:
由Sylvester结式知轨线经过平衡点时的临界值h满足方程
, (7)

Figure 3. Trajectories with ( ): (a) ; (b) ; (c) ; (d)
图3. ( )时轨线:(a) ;(b) ;(c) ;(d)
相应的判别式为 ,其中正数
。
当 时 ,方程 有三个实根,因判别式 , , ,其中正数
,
但一个二重实根 为增根,两个一重实根 和 分别对应平衡点 和 ,相应平衡点处Jacobi矩阵的行列式分别为 和 。表2说明了 时参数间关系。
Table 2. Relationship of parameters with α = α 1
表2. 时参数间关系
当 时 不存在,方程 仅有两个实根。引入变换 ,方程 化简为
, (8)
显然 有两个实根 和 ,即有 , 。由Jacobi矩阵的行列式 可知平衡点 的类型, ,另见表3。当然,利用 的符号也可说明。再考虑轨线过平衡点 时的临界值 ,简记 和 , ,作差有 ,其中对称函数
可得 和 的大小关系,见表3 (同表2)。图4给出了 时四种轨线图。
Table 3. Relationship of parameters with Δ x > 0 and α ≠ α 1
表3. 且 时参数关系
3.4. 情形3:
显然 。当 (或 )时轨线开口向左(或右),每支轨线的定义区间为 (或 ),且唯一的 随h增大而增大(或减小),而行波解是无界的。图5给出了 时两种轨线图。

Figure 4. Trajectories with : (a) ; (b) ; (c) ; (d)
图4. 时轨线图:(a) ;(b) ;(c) ;(d)
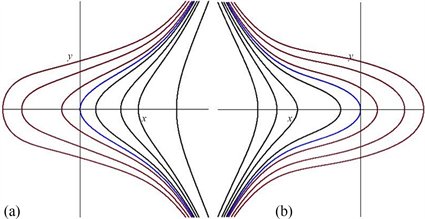
Figure 5. Trajectories with : (a) ; (b)
图5. 时轨线:(a) ;(b)
4. 行波解和对称
4.1. 行波解的分类及形式
为方便讨论行波解的形式,取变换 , ,由 可得标准形式
, , (9)
其中 是积分常数。根据五阶多项式完全判别系统法 [21] ,引入判别式
, , ,
,
, ,
可对行波解作分类并形式上给出解。
情形1: , , 。
这种情形存在,例如取 , 。此时 ,其中 , , 。当 时行波解的形式为
,(10)
其中 , 。
情形2: , 。
此即为 或 的情形,且 ,其中 , , 。当 时,行波解的形式为
(11)
其中 , , ,辅助函数 , 。
情形3: , 。
这种情形存在,例如取 , 。此时 ,a, , 及 是实数。当 时,如果 且 ,则行波解的形式为
; (12a)
如果 ,则行波解的形式为
; (12b)
如果 ,则行波解的形式为
。 (12c)
其中 , , 。
情形4: 。
这种情形存在,例如取 , 。此时 ,其中 , , , 及 是实数,行波解的形式为
。 (13)
情形5: , , 。
这种情形存在,例如取 , 。此时 ,a, , , 及 是实数,行波解的形式为
。 (14)
注意, 且 的情形不存在,因要求 ,否则 时退化为情形3。当 时,仅有情形3﹑情形4和情形5成立,因 。总之,行波解的形式由上述五类情形所规定。
4.2. 对称
引入变换 , 充分小,原方程的对称 应满足方程
, (15)
其中算子 定义为 。同上,考虑行波解 ,并引入mapping and deformation关系 [22] ,方程(15)可化为三阶ODE
, (16)
其中辅助函数 。上述常微分方程的通解形式为
, (17)
其中 ﹑ 和 是积分常数,而u是原方程(4)的行波解。因此有了以上行波解的分类工作,理论上是可以得到相应的对称 。
4.3. 近似解
Runge-Kutta法可以给出解的数值结果,但无法给出解的表达式;尽管同伦微扰法(HPM) [23] 和Adomian分解法(ADM) [24] [25] [26] [27] 可以给出近似解的幂级数表达式,对于结点情形尚可以采用,但收敛速度较慢,特别是在周期解情形,而一个物理系统中又常常考虑有界的行波解。给定初值 , ,对于系统(5),按文 [28] ,由HPM和ADM给出的前五阶近似解为
(18a)
(18b)
当然,也可用幂级数展开法得到上述结果。以 , , 为例,图6将这两种方法所得近似解与Runge-Kutta 45法进行比较,结果表明当 比较小时,近似可以接受。

Figure 6. Approximate solutions via HPM (black solid line), ADM (black dot line) and Runge-Kutta 45 method (red solid line): (a) ; (b)
图6. 同伦微扰法(黑色实线)﹑Adomian分解法(黑色点线)与Runge-Kutta 45法(红色实线)所得近似解:(a) ;(b)
鉴于行波解的表达式如此复杂,以及ADM和HPM的局限性,参照文 [29] [30] ,这里给出相应多模态近似解的计算方法。仍以上述 为例,取多模态近似解 ,其中w为频率, 。与文 [16] [29] [30] 不同,在一个周期 上对Hamilton函数 积分有 ,即可得耦合代数方程组
, (19a)
, (19b)
。 (19c)
结合初始条件 有解 , , 及 。图7(a)刻画了近似解(黑色实线)与实际解(红色点线)的近似程度,在前几个周期内两者非常吻合;图7(b)刻画了所得近似轨线(黑线)与实际周期轨(红线)之间的近似程度,近似程度很好。总之,这是一种有效的近似求解方法。类似的,理论上可以作出其它情形下的近似周期解。
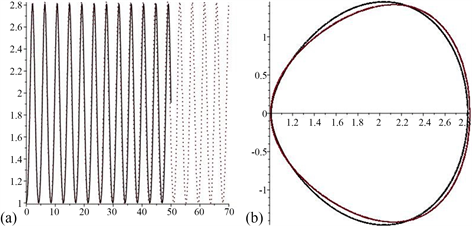
Figure 7. (a) Multimode approximate solution (black solid line); (b) periodic trajectory via multimode approximate solution (black line)
图7. (a) 多模态近似解(黑色实线);(b) 由多模态近似解所得周期轨(黑线)
5. 幂律n ZK方程的行波解
结合前几节的结果,类似于 时数形结合法对平衡点个数的讨论,本节研究幂律n ZK方程(2)及行波解对应的系统
, 。 (20)
首先考虑n为奇数情形。当 时,有2个平衡点 , , 。结合 的符号知:若 ,则 是鞍点, 是中心;若 ,则 是中心, 是鞍点。当 时,只有1个高阶奇点 ,因 ,同样是余维至少为4的尖点。当 时,没有平衡点。这样,平衡点可有0个﹑1个或2个。
再考虑n为偶数情形。同上,如果 ,则仅有一个平衡点,因 的单调性。如果 ,则:当 时,平衡点有3个;当 时,平衡点有2个;当 时,平衡点仅有1个。注意, 的情形包含在 的情形中。显然,可结合 的符号得到平衡点的类型(鞍点﹑中心或尖点),总结如下,与文 [16] 一致。
当 时,若 ,则唯一的平衡点 是中心;反之, 时 是鞍点。
当 时,设三个平衡点为 , , 。若 ( ﹑c同号),则 ﹑ 是中心,而 是鞍点;若 ,则 ﹑ 是鞍点,而 是中心。
当 时,设双曲平衡点为 ,退化平衡点为 , 或2, , ,同上 是余维至少为4的尖点;而 ( ﹑c同号)时 是中心,反之, 时 是鞍点。
总之,平衡点可有1个﹑2个或3个。图8描述了 时利用数形结合法对平衡点个数的分析。
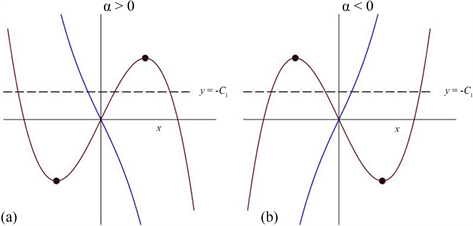
Figure 8. Analysis of number of equilibria with : (a) ; (b)
图8. 时平衡点个数分析:(a) ;(b)
此外,可以得到首次积分 ,当然,理论上也可使用除法定理获得,例如 时取 , 有 ,其中 和 均为待定常数。这样,轨线经过平衡点 时临界值h由方程组 , 决定,即临界值满足( )次代数方程
(21)
其中 , ,而行列式是 阶的。再结合高阶多项式完全判别系统法,理论上可说明h的实根情况及相应轨线的拓扑结构。同时,方程 的实根个数不少于方程 的实根个数,这也启发我们思考如下结论:
对于连续函数 和 ,若连续的轨线族 由微分方程 给出,h为实数,关于参数h的方程 由方程组 所确定,则方程 的实根个数(重根按单重根计算)不少于方程 的实根个数?除去 的增根,两者的“剩余”实根个数是否相等(存在“剩余”实根间的一一映射)?
例如,对于实数域上的多项式 和 , ,n为正整数,h为实数,则需要考虑“结式方程” 和方程 的实根情况。
因此,在给定参数条件下,可获得相图分支及光滑孤立波解、周期波解的存在性定理,详述如下。
定理1:当n为奇数, , (或 )时,对应系统(20)连接鞍点 (或 )的同宿轨道 (或 ),方程(2)有一个光滑孤立波解;对应系统(20)的周期轨道 ,h位于 和 之间,方程(2)有一族周期波解。
定理2:当n为偶数, , 时,对应系统(20)连接鞍点 和 的异宿轨道 ,方程(2)有一个扭(反扭)波解;对应系统(20)的周期轨道 ,h位于 (或 )和 之间,方程(2)有一族周期波解。
定理3:当n为偶数, , 时,对应系统(20)连接鞍点 的同宿轨道 ,方程(2)有两个光滑孤立波解;对应系统(20)环绕平衡点 ﹑ 和 的大范围周期轨道 , ,方程(2)有一族周期波解;对应系统(20)分别环绕中心 和 的两族周期轨道 ,h分别位于 和 及 和 之间,方程(2)有两族周期波解。
定理4:当n为偶数, , 时,对应系统(20)的周期轨道 , ,方程(2)有一族周期波解。
最后,原方程(2)的对称 应满足方程
, (22)
类似的,引入关系 后,其一般的表达式同(17),但 ,而u是原方程(2)的行波解。
6. 总结与讨论
文 [16] 的工作隐含了特征为0的实数域R上椭圆曲线 的若干思考。结合文 [6] [7] [16] ,本文整体上定性分析了幂律n ( 且为正整数)ZK方程行波解及其性质,对于其它非线性偏微分方程的研究具有一定参考意义,如(2 + 1)维广义Zakharov-Kuznetsovmodifiedequal-width (ZK-MEW)方程 [31]
。
致谢
感谢编辑和审稿人的工作,感谢温州大学赵敏老师和戴传军老师,感谢乐清市柳市镇第三中学郑孟老师和赵淑静老师,感谢乐清市城南中学陈谱锦老师。
文章引用
王双特,于恒国,刘环艺,戴文周. (3 + 1)维幂律3 Zakharov-Kuznetsov方程的行波解——兼论幂律n
Travelling Wave Solutions of a (3 + 1) Dimensional Zakharov-Kuznetsov Equation with Power Law 3—On Power Law n[J]. 应用数学进展, 2023, 12(04): 2020-2034. https://doi.org/10.12677/AAM.2023.124206
参考文献
- 1. 李康, 刘希强. (2+1)维扩展Zakharov-Kuznetsov方程的对称﹑约化和精确解[J]. 井冈山大学学报(自然科学版), 2015, 36(3): 29-33.
- 2. Mohammed, K.E. (2015) Deriving the New Traveling Wave Solutions for the Nonlinear Dis-persive Equation, KdV-ZK Equation and Complex Coupled KdV System Using Extended Simplest Equation Method. Communications in Theoretical Physics, 64, 379-390. https://doi.org/10.1088/0253-6102/64/4/379
- 3. 傅海明, 戴正德. Zakharov-Kuznetsov方程的新精确解[J]. 周口师范学院学报, 2013, 30(5): 4-7.
- 4. Dong, Z.Z., Chen, Y. and Lang, Y.H. (2010) Symmetry Reduction and Exact Solutions of the (3+1)-Dimensional Zakharov-Kuznetsov Equa-tion. Chinese Physics B, 19, Article ID: 090205. https://doi.org/10.1088/1674-1056/19/9/090205
- 5. 崔艳英, 吕大昭, 刘长河. (3+1)维Zakharov-Kuznetsov方程的Wronskian形式解[J]. 北京建筑工程学院学报, 2012, 28(2): 68-71.
- 6. 韦丽. 具有幂律非线性的(3+1)维Zakharov-Kuznetsov方程的行波解[J]. 应用数学进展, 2020, 9(9): 1426-1435.
- 7. Wei, L. and Ren, M.R. (2019) Bounded Traveling Wave Solutions of the (3+1)-Dimensional Zakharov-Kuznetsov Equation with Power Law Nonline-arity. Scholars Journal of Physics, Mathematics and Statistics, 7, 99-103. https://doi.org/10.36347/sjpms.2020.v07i07.004
- 8. Moslem, W.M., Ali, S., Shukla, P.K., et al. (2007) Solitary, Explosive, and Periodic Solutions of the Quantum Zakharov-Kuznetsov Equation and Its Transverse Instability. Physics of Plasmas, 14, Article ID: 082308. https://doi.org/10.1063/1.2757612
- 9. Lu, D.C., Seadawy, A.R., Arshad, M., et al. (2017) New Solitary Wave Solutions of (3+1)-Dimensional Nonlinear Extended Zakharov-Kuznetsov and Modified KdV-Zakharov-Kuznetsov Equations and Their Applications. Results in Physics, 7, 899-909. https://doi.org/10.1016/j.rinp.2017.02.002
- 10. 黄欣. 首次积分法下高维非线性偏微分方程新的行波解[J]. 四川师范大学学报(自然科学版), 2014, 37(3): 312-315.
- 11. Li, H., Sun, S.R. and Wang, K.M. (2011) Bifurcations of Traveling Wave Solutions for the Generalized Zakharov-Kuznetsov Equation. 2011 IEEE International Conference on Intelligent Computing and Intelligent Systems, Vol. 1, 102-107. https://doi.org/10.1109/ICMT.2011.6002021
- 12. Zhang, W.B. and Zhou, J.B. (2012) Traveling Wave Solutions of a Generalized Zakharov-Kuznetsov Equation. ISRN Mathematical Analysis, 2012, Article ID: 107846. https://doi.org/10.5402/2012/107846
- 13. 冯庆江, 李岩, 杨利盎. 用试探函数法求Zakharov-Kuznetsov方程的孤子解[J]. 长春大学学报, 2010, 20(6): 8-9.
- 14. Yan, Z.L. and Liu, X.Q. (2006) Symmetry Reductions and Explicit Solutions for a Generalized Zakharov-Kuznetsov Equation. Communications in Theoretical Physics, 45, 29-32. https://doi.org/10.1088/0253-6102/45/1/004
- 15. 洪宝剑. KdV方程和Zakharov-Kuznetsov方程新的椭圆函数解[J]. 南京工程学院学报(自然科学版), 2010, 8(1): 1-7.
- 16. 王双特, 于恒国. (3+1)维修正KdV-Zakharov-Kuznetsov方程的行波解[J]. 动力学与控制学报, 2022, 20(2): 36-44.
- 17. Feng, Z.S. (2002) The First Integral Method to Study the Burgers-Korteweg-de Vries Equation. Physics Letters A, 35, 343-349. https://doi.org/10.1088/0305-4470/35/2/312
- 18. Feng, Z.S. (2003) The First Integral Method to the Two-Dimensional Burgers-Korteweg-de Vries Equation. Physics Letters A, 308, 173-178. https://doi.org/10.1016/S0375-9601(03)00016-1
- 19. 马知恩, 周义仓. 常微分方程定性与稳定性方法[M]. 北京: 科学出版社, 2001: 115-116.
- 20. Huang, J.C., Gong, Y.J. and Chen, J. (2013) Multiple Bifurcations in a Preda-tor-Prey System of Holling and Leslie Type with Constant-Yield Prey Harvesting. International Journal of Bifurcation and Chaos, 23, Article ID: 1350164. https://doi.org/10.1142/S0218127413501642
- 21. Liu, C.S. (2008) Direct Integral Method, Complete Discrimina-tion System for Polynomial and Applications to Classifications of All Single Traveling Wave Solutions to Nonlinear Dif-ferential Equations: A Survey.
- 22. Xiao, N.G. and Lou, S.Y. (2012) Bosonization of Supersymmetric KdV Equation. Physics Letters B, 707, 209-215. https://doi.org/10.1016/j.physletb.2011.12.021
- 23. He, J.H. (1999) Homotopy Perturbation Technique. Computer Methods in Applied Mechanics and Engineering, 178, 257-262. https://doi.org/10.1016/S0045-7825(99)00018-3
- 24. Biazar, J. and Montazeri, R. (2005) A Computational Method for Solution of the Prey and Predator Problem. Applied Mathematics and Computation, 163, 841-847. https://doi.org/10.1016/j.amc.2004.05.001
- 25. Wazwaz, A.-M. (2005) Adomian Decomposition Method for a Re-liable Treatment of the Bratu-Type Equations. Applied Mathematics and Computation, 166, 652-663. https://doi.org/10.1016/j.amc.2004.06.059
- 26. Biazar, J., Babolian, E., Nouri, A. and Islam, R. (2003) An Alter-nate Algorithm for Computing Adomian Decomposition Method in Special Cases. Applied Mathematics and Computa-tion, 138, 523-529. https://doi.org/10.1016/S0096-3003(02)00174-1
- 27. Biazar, J., Tango, M., Babolian, E. and Islam, R. (2003) So-lution of the Kinetic Modeling of Lactic Acid Fermentation Using Adomian Decomposition Method. Applied Mathemat-ics and Computation, 139, 249-258. https://doi.org/10.1016/S0096-3003(02)00173-X
- 28. 王双特, 于恒国. 利用同伦微扰法和Adomian分解法求解捕食生态模型[J]. 高师理科学刊, 2021, 41(7): 14-19.
- 29. 楼智美, 王元斌, 俞立先. 一类强非线性二阶微分方程的多模态近似解析解研究[J]. 动力学与控制学报, 2019, 17(5): 463-466.
- 30. Durmaz, S., Altay, D.S. and Kaya, M.O. (2010) High Order Hamiltonian Approach to Nonlinear Oscillators. International Journal of Nonlinear Sci-ences and Numerical Simulation, 11, 565-570. https://doi.org/10.1515/IJNSNS.2010.11.8.565
- 31. 肖军均, 冯大河, 孟霞. 广义ZK-MEW方程的行波解分支[J]. 桂林电子科技大学学报, 2016, 36(1): 66-70.
