Pure Mathematics
Vol.4 No.04(2014), Article
ID:13856,5
pages
DOI:10.12677/PM.2014.44021
The Fourier Transform and Its Application
School of Mathematics and Computer Science, Shanxi Normal University, Linfen
Email: caoruihua0056@126.com
Copyright © 2014 by author and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received: Jun. 14th, 2014; revised: Jul. 12th, 2014; accepted: Jul. 19th, 2014
ABSTRACT
Fourier transformation is not only a very important integral transformation, but also is an important mathematics method. In many branches of Mathematics, Fourier transformation plays an important role, such as partial differential equations, probability, complex variable functions and mathematical analysis. Firstly, this paper simply introduces the concept of Fourier transform and its basic nature, whereafter the author introduces its application in partial differential equation.
Keywords:Fourier Transformation, Partial Differential Equation

傅里叶变换及其应用
曹瑞华
山西师范大学数学与计算机科学学院,临汾
Email: caoruihua0056@126.com
收稿日期:2014年6月14日;修回日期:2014年7月12日;录用日期:2014年7月19日

摘 要
傅立叶变换不仅是一个非常重要的积分变换,而且是一种重要的数学方法。在数学领域的许多分支,傅里叶变换都起着非常重要的应用,如偏微分方程、概率、复变函数与数学分析。本文首先简单介绍了傅里叶变换的概念及其基本性质,然后给出了它在偏微分方程中的一些应用。
关键词
傅里叶变换,偏微分方程

1. 引言
L. kelvin说:傅里叶理论不仅是现代分析中最美妙的结果之一,而且可以说,它为现代物理中每一个深奥问题的处理提供了一件必不可少的工具。随着近代物理的飞速发展,越来越多的实际问题需要用偏微分方程的理论来解决。如尖端的激光理论,生物数学和非线性科学中的许多问题等。为了求解这些复杂的方程,得到它们解的表达式,傅里叶变换成了主要的工具,它在庞大的偏微分理论系统中闪耀着光芒。傅里叶变换是一类重要的积分变换,而积分变换能够将分析运算转化为代数运算,正是由于积分变换这一特性,在微分方程、偏微分方程的求解中成为重要的方法之一。用傅里叶变换求解偏微分方程就如同用对数变换计算数量的乘积或商一样简便,在这种变换下,偏微分方程可以减少自变量的个数直至变成常微分方程。
2. 傅里叶变换的概念及基本性质[1]-[5]
傅里叶变换能将满足一定条件的某个函数表示成三角函数(正弦或余弦函数)或者它们的积分的线性组合。在不同的研究领域,傅里叶变换具有多种不同的变体形式,如连续傅里叶变换和离散傅里叶变换。
2.1. 连续傅里叶变换的概念
定义:假使函数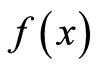 在
在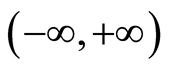 内绝对可积,我们称
内绝对可积,我们称 是
是 的傅里叶变换,并把它记为
的傅里叶变换,并把它记为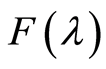 或
或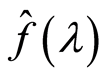 ,即:
,即: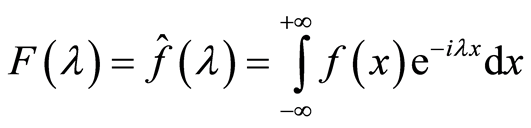 。并称
。并称 为
为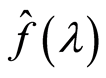 的傅里叶逆变换。
的傅里叶逆变换。
2.2. 离散傅里叶变换的概念
定义:设 为周期为
为周期为![]() 的周期序列,则称和式
的周期序列,则称和式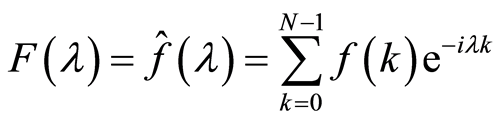 (
( 为整数)为
为整数)为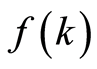 的离散傅里叶变换。并称
的离散傅里叶变换。并称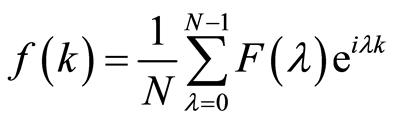 为
为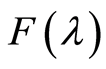 的离散的傅里叶逆变换。
的离散的傅里叶逆变换。
2.3. 连续傅里叶变换的性质
1) 线性性质
设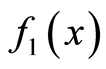 和
和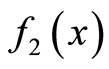 的傅里叶变换分别为
的傅里叶变换分别为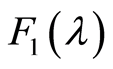 和
和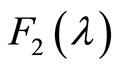 ,则:
,则:
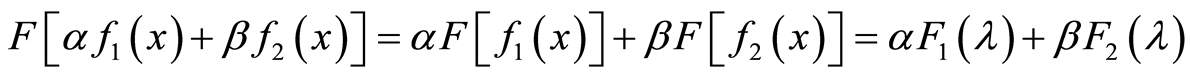
其中 为常数。
为常数。
2) 微分性质
如果 都是可以进行傅里叶变换的,设
都是可以进行傅里叶变换的,设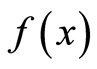 的傅里叶变换为
的傅里叶变换为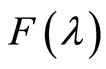 ,而且当
,而且当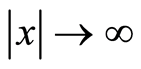 时,
时, ,则有
,则有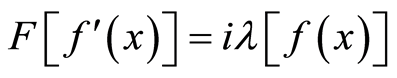 。
。
3) 卷积性质
设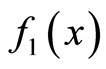 和
和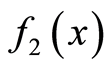 的傅里叶变换分别为
的傅里叶变换分别为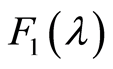 和
和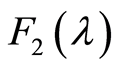 ,证明:
,证明: 和
和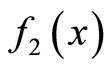 的卷积的傅里叶变换等于
的卷积的傅里叶变换等于 和
和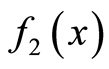 的傅里叶变换的乘积,即:
的傅里叶变换的乘积,即: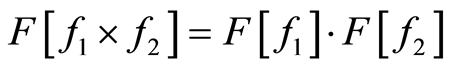 。
。
4)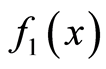 和
和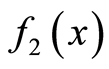 乘积的傅里叶变换等于
乘积的傅里叶变换等于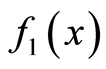 和
和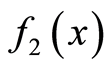 的傅里叶变换的卷积乘以
的傅里叶变换的卷积乘以 ,即:
,即:
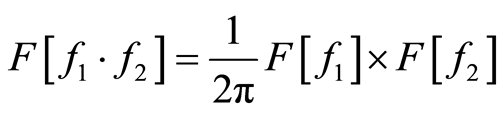 。
。
5) 若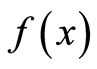 及
及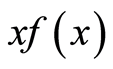 都可以进行傅里叶变换,那么:
都可以进行傅里叶变换,那么:
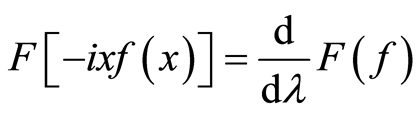 。
。
6) 平移性质
设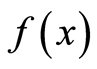 的傅里叶变换为
的傅里叶变换为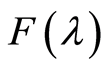 ,求证:
,求证: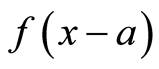 的傅里叶变换为
的傅里叶变换为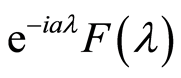 。
。
证明:

此性质表明平移后的傅里叶变换等于未作平移的傅里叶变换乘以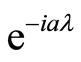 。
。
2.4. 离散傅里叶变换的性质
1) 线性性质
设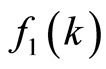 和
和 均为周期为
均为周期为![]() 的序列,对任意给定的常数
的序列,对任意给定的常数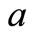 和
和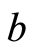 ,则下式成立:
,则下式成立:

2) 平移性质
对任意的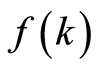 ,则:
,则:

3)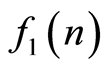 与
与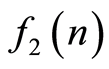 卷积的离散的傅里叶变换等于
卷积的离散的傅里叶变换等于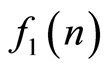 与
与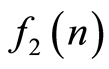 的傅里叶变换的乘积,即:
的傅里叶变换的乘积,即:
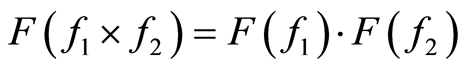
4)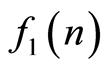 与
与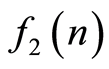 乘积的傅里叶变换等于
乘积的傅里叶变换等于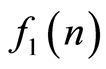 与
与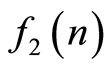 的傅里叶变换的卷积乘以
的傅里叶变换的卷积乘以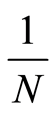 ,即:
,即:
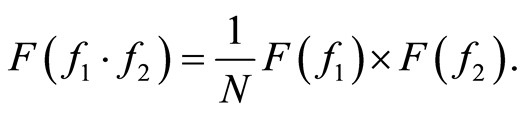
3. 傅里叶变换在求解偏微分方程中的应用
在求偏微分方程的解时,如果当自变量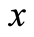 的取值范围是无穷区间
的取值范围是无穷区间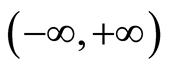 时可以考虑对方程中的
时可以考虑对方程中的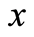 采用傅里叶变换,这时被变换的函数还应满足当
采用傅里叶变换,这时被变换的函数还应满足当 时趋于0,而且对二阶的方程还要求被变换的函数的一阶导数也趋于0。
时趋于0,而且对二阶的方程还要求被变换的函数的一阶导数也趋于0。
用傅里叶变换求解偏微分方程的步骤大致为:1) 对定解问题作傅里叶变换;2) 求解象函数;3) 对象函数作傅里叶逆变换得到原问题的解。
3.1. 求解波动方程
例1. 已知两端无界弦振动的初始位移为 ,初始速度为0,试求弦在任一时刻
,初始速度为0,试求弦在任一时刻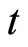 的纵向位移
的纵向位移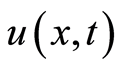 ,即解以下偏微分定解问题:
,即解以下偏微分定解问题:
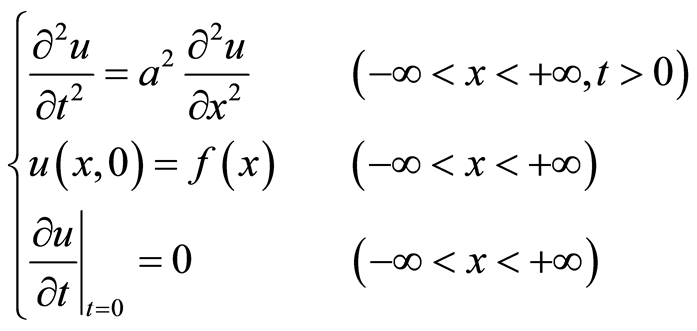
解:对 作傅里叶变换,令
作傅里叶变换,令 ,则
,则
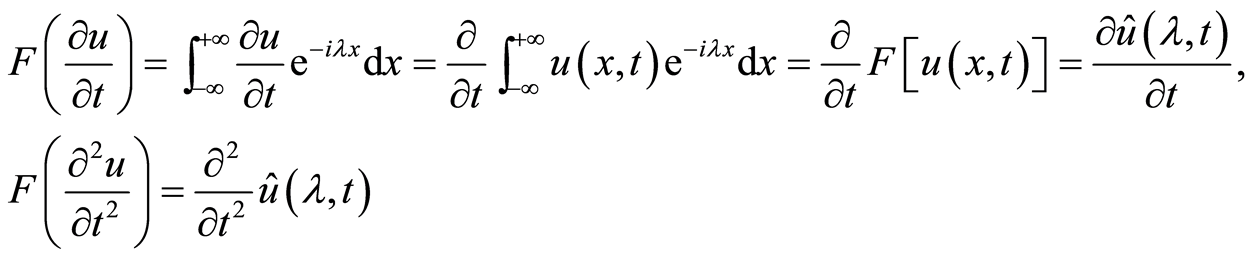 ,
,
由问题的物理意义知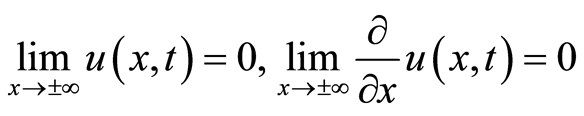 ,利用傅里叶变换的微分性质得
,利用傅里叶变换的微分性质得
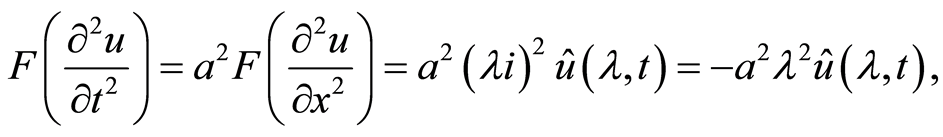
因此,原定解问题变为
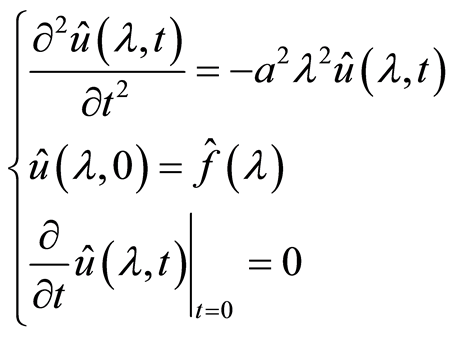
把 看成常数,即
看成常数,即
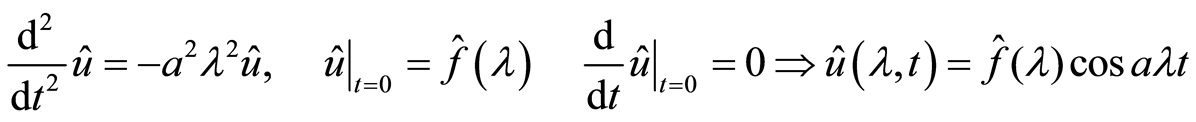
再由傅里叶逆变换公式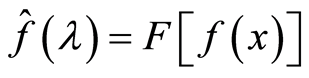 ,得到
,得到

3.2. 求解热传导方程
例2. 求解二维热传导方程的初值问题
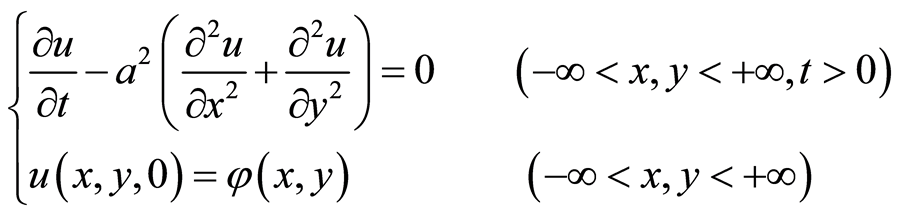
解:因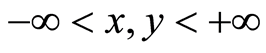 ,故对
,故对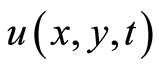 ,
,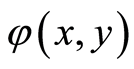 关于
关于![]() 作傅里叶变换,记:
作傅里叶变换,记:
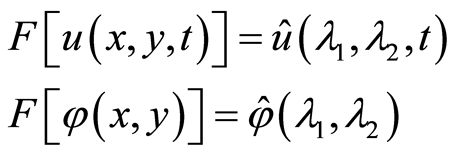
从而得到关于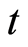 的一阶常微分方程的初值问题
的一阶常微分方程的初值问题

它的解为 将上式对
将上式对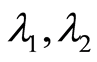 取傅里叶逆变换,得
取傅里叶逆变换,得
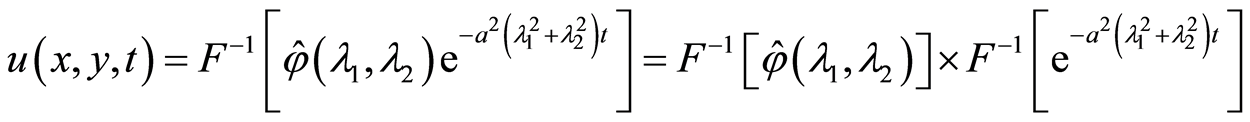
因为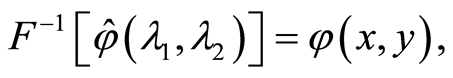
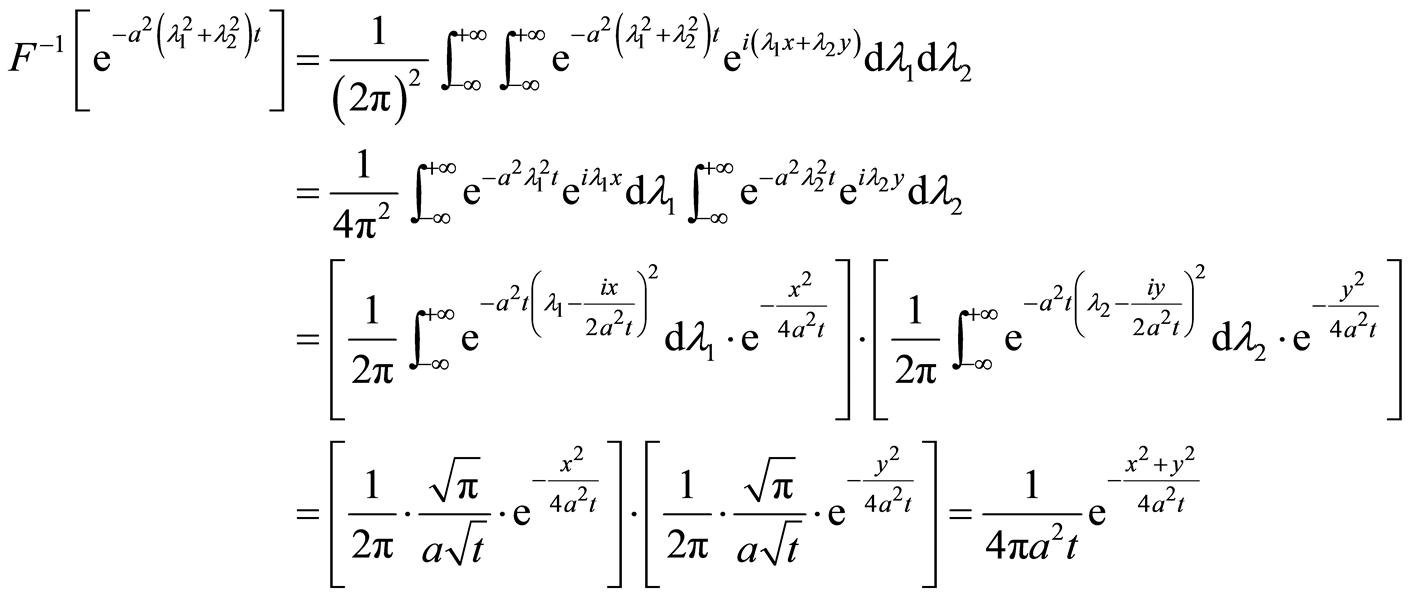

由此得出初值问题的解为

3.3. 求解半平面的Dirichlet问题[6] [7]
例3. 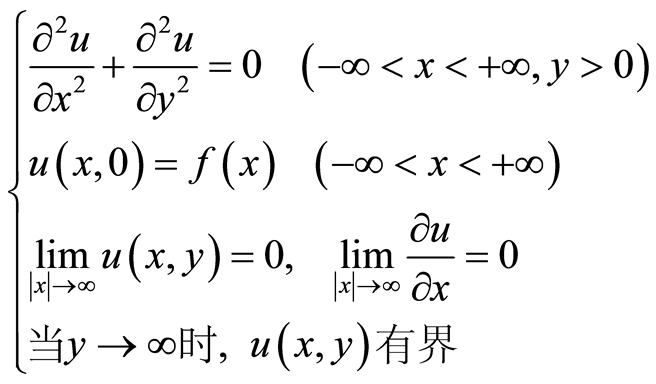
解:令 由傅里叶变换的性质,则有
由傅里叶变换的性质,则有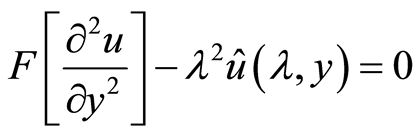
而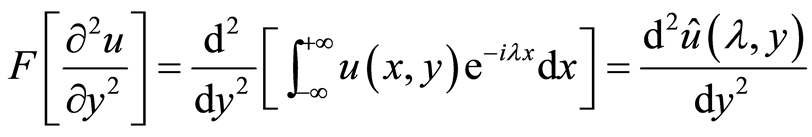 ,由此可得
,由此可得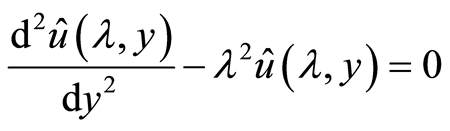
这是一个带有参数![]() 的二阶常微分方程,其通解为
的二阶常微分方程,其通解为 ,因为当
,因为当![]() 时
时 是有界的,所以当
是有界的,所以当![]() 时,
时,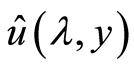 也必须有界,故当
也必须有界,故当![]() ,
,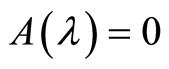 ,且
,且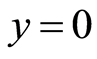 时,有
时,有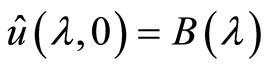 。
。
当![]() 时,有
时,有 ,且当
,且当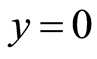 时,有
时,有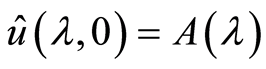
因此对于任何![]() 都有
都有
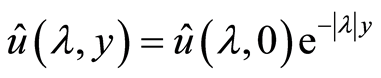
又因为
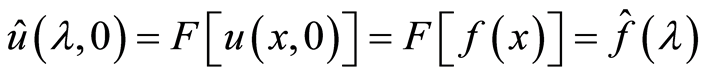
故有
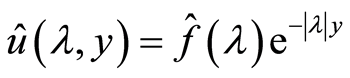
从而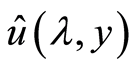 的傅里叶逆变换为
的傅里叶逆变换为

这里我们利用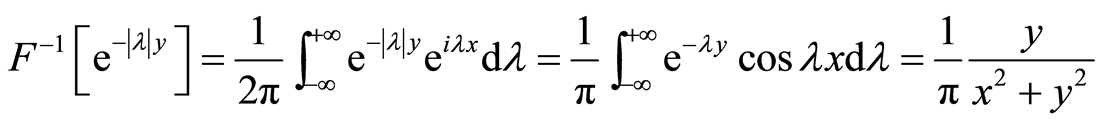
因此,在上半平面y > 0上狄里克莱问题的解是:

4. 结论
在这篇文章中,我们主要介绍了傅里叶变换的概念、基本性质和它在偏微分方程中的应用。傅里叶变换不仅在数学中有广泛的应用,而且在电气工程、电子工程、信息与通信工程、控制工程、生物医学工程、天文学等理工类学科中也有非常重要的的应用。
参考文献 (References)
- 冷建华 (2004) 傅里叶变换. 清华大学出版社, 北京, 73-84.
- [美]罗纳德·N·布雷斯韦尔著 (2005) 傅里叶变换及其应用. 殷勤业, 张建国译. 西安交通大学出版社, 西安, 84-103.
- 陈传璋, 金福临, 朱学炎等编 (1986) 数学分析(第二版). 高教出版社, 北京, 121-126.
- (美)哈伯曼著 (2007) 实用偏微分方程(第四版). 郇中丹, 李援南, 刘歆等译. 机械工业出版社, 北京, 308-334.
- 查中伟 (2005) 数学物理偏微分方程. 西南交通大学出版社, 成都, 93-103.
- 谷超豪, 李大潜, 陈恕行等 (2002) 数学物理方程(第二版). 高等教育出版社, 北京, 54-57.
- 谢惠民, 易发槐, 钱定边等 (2004) 数学分析与讲义. 高等教育出版社, 北京, 79-105.