Pure Mathematics
Vol.05 No.02(2015), Article ID:14935,6
pages
10.12677/PM.2015.52010
Characterizations of Superabundant Semigroups
Yonglin Hou1, Wenjuan Guo2, Xiaojiang Guo1
1College of Mathematics and Information Science, Jiangxi Normal University, Nanchang Jiangxi
2College of Education, Jiangxi Normal University, Nanchang Jiangxi
Email: 837851973@qq.com, 584753648@qq.com, xjguo@jxnu.edu.cn
Received: Feb. 28th, 2015; accepted: Mar. 8th, 2015; published: Mar. 12th, 2015
Copyright © 2015 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
Superabundant semigroups are generalizations of completely regular semigroups. Compared with completely regular semigroups, there are many topics on superabundant semigroups which are worth to probing. In this paper some characterizations of superabundant semigroups are obtained.
Keywords:Abundant Semigroup, Superabundant Semigroup, Completely  -Simple Semigroup
-Simple Semigroup

超富足半群的若干特征
侯永林1,郭文娟2,郭小江1
1江西师范大学,数学与信息科学学院,江西 南昌
2江西师范大学,教育学院,江西 南昌
Email: 837851973@qq.com, 584753648@qq.com, xjguo@jxnu.edu.cn
收稿日期:2015年2月28日;录用日期:2015年3月8日;发布日期:2015年3月12日

摘 要
超富足半群是完全正则半群的推广,对照完全正则半群,超富足半群有许多问题值得探索。本文给出超富足半群的若干特征。
关键词 :富足半群,超富足半群,完全 -单半群
-单半群

1. 引言
半群 称为富足半群(abundant semigroup) [1] [2] ,如果
称为富足半群(abundant semigroup) [1] [2] ,如果 的每一个
的每一个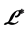 -类和每一个
-类和每一个 -类都含有幂等元。进一步,富足半群称为超富足半群(superabundant semigroup),如果它的每个
-类都含有幂等元。进一步,富足半群称为超富足半群(superabundant semigroup),如果它的每个 -类都含有幂等元。正则半群是富足半群,而超富足半群是完全正则半群(completely regular semigroup)的推广。如[2] ,我们称消去幺半群(cancellative monoid)上的Rees矩阵半群的半群为完全
-类都含有幂等元。正则半群是富足半群,而超富足半群是完全正则半群(completely regular semigroup)的推广。如[2] ,我们称消去幺半群(cancellative monoid)上的Rees矩阵半群的半群为完全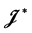 -单半群(completely
-单半群(completely  -simple semigroup) 关于这类半群,可参见[3] 。J.B. Fountain [2] 指出:富足半群为超富足半群的充分必要条件是它同构于一些完全
-simple semigroup) 关于这类半群,可参见[3] 。J.B. Fountain [2] 指出:富足半群为超富足半群的充分必要条件是它同构于一些完全 -单半群的半格。
-单半群的半格。
完全正则半群表示为一些子群的无交并。可以说,完全正则半群是一类离“群”较近的半群。又由于完全正则半群是群上Rees矩阵半群的半格,所以具有许多“矩阵”特性。这些特性足以让完全正则半群成为半群理论中的重要研究课题。事实上,许多著名半群论学者开展了完全正则半群的研究工作,也具有非常丰富的研究成果(详见[4] )。对照完全正则半群,我们对超富足半群的了解就太少了。本文希望能做一些“弥补”,将给出超富足半群的一些特征。
2. 若干准备
本文将用教科书[5] ,[6] 和文[2] 的术语和符号。首先回忆一些将不断引用的已知结论。
引理2.1 [2] :令 为半群,且
为半群,且 ,
, ,则
,则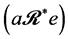
 当且仅当对于任意的
当且仅当对于任意的 ,
,
 且
且 .
.
众所周知, 为右同余,而
为右同余,而 为左同余。一般的,
为左同余。一般的,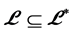 ,
, 。但当
。但当 ,
, 为正则元时,
为正则元时, 当且仅当
当且仅当 。如[2] ,定义
。如[2] ,定义 ,
, 。另外,当
。另外,当 记
记 ,
, ,
, 之一时,我们将记
之一时,我们将记 为含
为含 的
的 的
的 -类。并且,用
-类。并且,用 记
记 的所有幂等元集。
的所有幂等元集。
半群 的左理想
的左理想 称为左
称为左 -理想(left
-理想(left 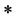 -ideal),如果
-ideal),如果 。对偶的,定义右
。对偶的,定义右 -理想(right
-理想(right  - ideal)。半群
- ideal)。半群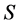 的理想如果既是左
的理想如果既是左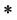 -理想,又是右
-理想,又是右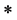 -理想,则称为
-理想,则称为 -理想(
-理想( -ideal)。对于
-ideal)。对于 ,我们将用
,我们将用 记含
记含 的最小
的最小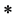 -理想。定义
-理想。定义
 当且仅当
当且仅当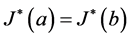 .
.
我们称仅有一个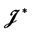 -类的半群为
-类的半群为 -单半群。事实上,半群为
-单半群。事实上,半群为 -单的充分必要条件是它仅有一个
-单的充分必要条件是它仅有一个 -理想。令
-理想。令 。易知,
。易知, 是
是 的
的 -理想。称Rees商半群
-理想。称Rees商半群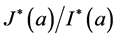 为由
为由 确定的
确定的 的
的 -主因子(principal
-主因子(principal 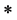 -factor)。
-factor)。
下面的引理可由([7] , Lemma 3.5)直接得到。
引理2.2:富足半群的所有主 -因子都是富足半群。
-因子都是富足半群。
令 为非空集合,
为非空集合,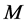 为消去幺半群,且
为消去幺半群,且 是元为
是元为 的单位(unit)的
的单位(unit)的 -矩阵。在集合
-矩阵。在集合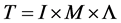 上,定义运算:
上,定义运算:
 .
.
关于运算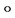 ,
, 构成富足半群,称之为消去幺半群
构成富足半群,称之为消去幺半群 上的关于夹心矩阵
上的关于夹心矩阵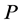 的Rees矩阵半群,记为
的Rees矩阵半群,记为 。如[2] ,我们称同构于消去幺半群上的Rees矩阵半群为完全
。如[2] ,我们称同构于消去幺半群上的Rees矩阵半群为完全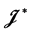 -单半群。等价地,半群是完全
-单半群。等价地,半群是完全 -单半群当且仅当它是
-单半群当且仅当它是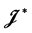 -单的超富足半群。
-单的超富足半群。
引理2.3:任一完全 -单半群的所有正则元构成完全单子半群。
-单半群的所有正则元构成完全单子半群。
证明:仅需证,消去幺半群 上的关于夹心矩阵
上的关于夹心矩阵 的Rees矩阵半群
的Rees矩阵半群 的正则元集构成完全单子半群。令
的正则元集构成完全单子半群。令 。若
。若 为正则元,则存在
为正则元,则存在 使得
使得

即 。比较分量,得
。比较分量,得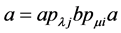 ,进而
,进而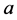 为
为 的正则元,于是
的正则元,于是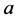 为
为 的单位。反之,容易验证,当
的单位。反之,容易验证,当 为单位,则
为单位,则 为正则元。故
为正则元。故 的正则元集为
的正则元集为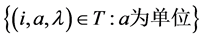 。不难看出,
。不难看出, 的正则元集构成子半群,且为
的正则元集构成子半群,且为 ,其中
,其中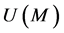 为
为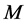 的所有单位组成的子群,从而
的所有单位组成的子群,从而 的正则元集构成完全单子半群。
的正则元集构成完全单子半群。
引理2.4 ([2] , proposition 6.9)设半群 为半群
为半群 的半格,则下面三款中任意两款可以推出第三款:
的半格,则下面三款中任意两款可以推出第三款:
(1) 为富足半群;
为富足半群;
(2) 对于任意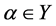 ,
, 为富足半群;
为富足半群;
(3) 对于任一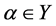 ,
, ,总有
,总有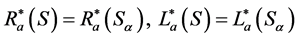 。
。
下面已知结论将会用到。
引理2.5:令 为超富足半群,则
为超富足半群,则
(1) ([2] ,Corollary 6.2, Proposition 6.5] ;
;
(2) ([2] , Corollary 6.1 and 6.4] 。
。
富足半群 称为幂等元连接的(idempotent-connected),如果对于任意的
称为幂等元连接的(idempotent-connected),如果对于任意的 和任意(存在)
和任意(存在) ,
, ,存在双射
,存在双射 使得
使得 ,对所有
,对所有 ,其中
,其中 为由集合
为由集合 生成的
生成的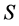 的子半群。事实上,
的子半群。事实上, 是半群同构。这一观察很重要,以后将会多次用到。以下总成
是半群同构。这一观察很重要,以后将会多次用到。以下总成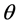 为关于
为关于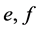 的
的 连接同构。若需要强调
连接同构。若需要强调 时,则记此连接同构为
时,则记此连接同构为 。文献[8] 给出了这类半群的许多特征。
。文献[8] 给出了这类半群的许多特征。
3. 主要结果
本文将给出超富足半群的一些特征。
命题3.1:超富足半群所有正则元构成完全正则子半群。
证明:设 为超富足半群,且
为超富足半群,且 为分
为分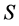 为完全
为完全 -单半群的半格分解。若为命题3.1,据引理2.3,仅需证:
-单半群的半格分解。若为命题3.1,据引理2.3,仅需证: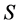 的幂等元乘积为正则元。为此,令
的幂等元乘积为正则元。为此,令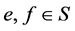 为幂等元,则存在
为幂等元,则存在 使得
使得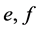 分别为
分别为 的幂等元。但
的幂等元。但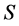 为富足半群,于是有幂等元
为富足半群,于是有幂等元 使得
使得 ,结合
,结合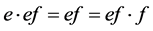 ,我们有
,我们有 ,进而
,进而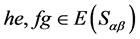 ,再据引理2.3,
,再据引理2.3,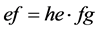 为
为 的正则元,从而
的正则元,从而 为
为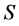 的正则元。
的正则元。
令 为所有非负整数组成的集合。记
为所有非负整数组成的集合。记
 .
.
在集合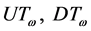 上,定义运算
上,定义运算
 .
.
通常验证, 都是半群。事实上,它们都是双循环半群(bicyclic semigroup)的全子半群,于是均为富足半群。由([9] , Example 2.6),知
都是半群。事实上,它们都是双循环半群(bicyclic semigroup)的全子半群,于是均为富足半群。由([9] , Example 2.6),知 都不是超富足半群。这说明,命题3.1的逆不成立。
都不是超富足半群。这说明,命题3.1的逆不成立。
定理3.2:令 为富足半群,则
为富足半群,则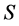 为超富足半群当且仅当关于
为超富足半群当且仅当关于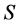 的乘法,
的乘法,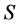 的每一个
的每一个 -类都构成完全
-类都构成完全 -单半群。
-单半群。
证明:据([2] , Theorem 6.8],仅需证充分性。为此,设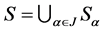 为半群
为半群 关于
关于 的分类,则每一
的分类,则每一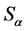 均为完全
均为完全 -单半群。类似于命题3.1的证明,
-单半群。类似于命题3.1的证明,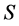 的所有正则元构成
的所有正则元构成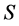 的子半群。
的子半群。
首先。证明:对于任意 ,
,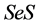 是
是 的
的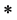 -理想。
-理想。
令 且
且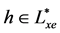 ,据
,据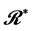 是左同余,则有
是左同余,则有 。而
。而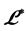 为右同余,于是
为右同余,于是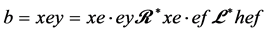 。若
。若 ,则
,则 ,显然,存在
,显然,存在 使得
使得 。前面已经证明:
。前面已经证明: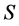 的所有正则元构成子半群,于是
的所有正则元构成子半群,于是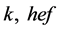 均为
均为 的正则元。注意到,
的正则元。注意到,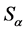 为完全
为完全 -单半群,再由引理3.1,知在
-单半群,再由引理3.1,知在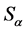 中,
中,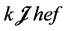 ,于是存在
,于是存在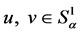 使得
使得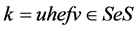 ,但
,但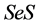 为理想,从而
为理想,从而 为
为 的右
的右 -理想。类似的,
-理想。类似的, 为
为 的左
的左 -理想。因此
-理想。因此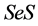 为
为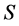 的
的 -理想。
-理想。
其次,证明: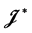 是
是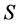 的半格同余。
的半格同余。
事实上, 当且仅当存在
当且仅当存在 使得
使得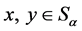 。据此,不难知道:
。据此,不难知道: ,
, ,即
,即 ,
, 。下面证明,
。下面证明,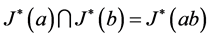 。由
。由 为富足半群,知有
为富足半群,知有 使得
使得 ,显然,
,显然, 。据上面的证明,知
。据上面的证明,知 ,进而
,进而 。另一方面,
。另一方面, -理想的交还是
-理想的交还是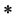 -理想,以及
-理想,以及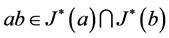 ,有
,有 。反之,若
。反之,若 ,则存在
,则存在 使得
使得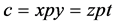 ,于是
,于是

进而 ,于是
,于是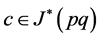 。考虑到,
。考虑到, 分别为右同余和左同余,我们有
分别为右同余和左同余,我们有 ,进而
,进而 。因此
。因此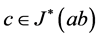 ,以致于
,以致于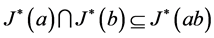 。从而
。从而 。现在对于
。现在对于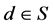 ,若
,若 ,总有
,总有

于是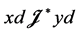 ,从而
,从而 是右同余。类似地,
是右同余。类似地,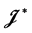 是左同余。故
是左同余。故 为
为 上的半格同余。
上的半格同余。
至此,我们证明了: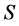 是半群
是半群 的半格。因为
的半格。因为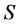 和所有的
和所有的 都是富足半群,再根据引理2.4,
都是富足半群,再根据引理2.4, 。但
。但 为完全
为完全 -单半群,从而
-单半群,从而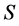 为超富足半群。
为超富足半群。
对于半群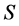 ,
, ,由于
,由于 ,易知
,易知 。不难知道,
。不难知道, 为完全
为完全 -单半群附加零元当且仅当
-单半群附加零元当且仅当 为完全
为完全 -单子半群。基于定理3.2,下面的定理是显然的。
-单子半群。基于定理3.2,下面的定理是显然的。
定理3.3:令 为富足半群,则
为富足半群,则 为超富足半群当且仅当
为超富足半群当且仅当 的每个主
的每个主 -因子都是完全
-因子都是完全 -单子半群附加零元。
-单子半群附加零元。
设 为半群
为半群 的幂等元。定义
的幂等元。定义
 当且仅当
当且仅当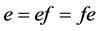 .
.
众所周知,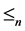 是集合
是集合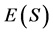 上的偏序。非零幂等元
上的偏序。非零幂等元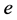 称为本原的(primitive),如果对于任意幂等元
称为本原的(primitive),如果对于任意幂等元 ,若
,若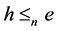 ,则
,则 或
或 (当
(当 有零元0)。半群称为本原的 [6] ,如果它的所有非零幂等元都是本原的。
有零元0)。半群称为本原的 [6] ,如果它的所有非零幂等元都是本原的。
富足半群 的子半群
的子半群 称为
称为 -子半群(
-子半群( -subsemigroup),如果对于任意
-subsemigroup),如果对于任意 ,存在
,存在 使得
使得 。显然,任意
。显然,任意 -子半群都是富足半群。
-子半群都是富足半群。
引理3.4:令 为幂等元连接富足半群,
为幂等元连接富足半群, 且
且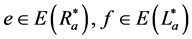 。若
。若 且
且 为
为 的关于
的关于 的连接同构,则集合
的连接同构,则集合 构成
构成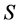 的
的 -子半群,且同构于
-子半群,且同构于 。
。
证明:注意到,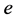 和
和 分别为子半群
分别为子半群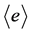 和
和 的恒等元。但
的恒等元。但 为
为 到
到 上的同构,于是
上的同构,于是 。显然,
。显然, ,这样
,这样 。继续这一过程,我们有:对于任意正整数
。继续这一过程,我们有:对于任意正整数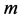 ,
, 且
且 。因为
。因为 ,所以
,所以 ,换言之,
,换言之, 。另外,可归纳地证明:
。另外,可归纳地证明:
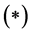 对于正整数
对于正整数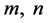 ,若
,若 ,则
,则 。
。
令 ,且
,且 。若
。若 ,则
,则
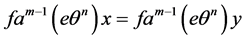
即 。因为
。因为 为
为 的关于
的关于 的连接同构,所以
的连接同构,所以 ,进而
,进而 ,故
,故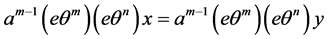 ,再据
,再据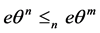 ,从而
,从而 。重复这一过程,
。重复这一过程, 。另一方面,
。另一方面, .故
.故 。
。
若有 ,则
,则 ,进而
,进而

即 。重复这一过程,
。重复这一过程, ,这样
,这样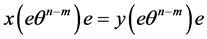 ,即
,即 。而
。而
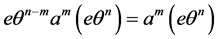
从而 。
。
考虑到, 为连接同构。对于
为连接同构。对于 ,
,

后面两个等式都是由事实 得到。这意味着,
得到。这意味着,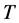 为
为 的子半群。而我们已证:
的子半群。而我们已证:
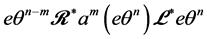
故 为
为 -子半群。
-子半群。
定义

显然, 有定义。对于任意
有定义。对于任意 ,进而
,进而 为满射。
为满射。
令 ,若
,若 ,即
,即 ,则
,则
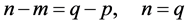
进而 ,从而
,从而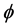 为单射。
为单射。
据前面的证明,当 ,即
,即 ,则由
,则由

可得

同理,当 ,即
,即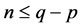 ,则
,则

因此 为半群同态。故
为半群同态。故 为半群同构。
为半群同构。
对偶的,我们有
引理3.5:令 为幂等元连接富足半群,
为幂等元连接富足半群, 且
且 。若
。若 且
且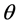 为
为 的关于
的关于 的连接同构,则集合
的连接同构,则集合 构成
构成 的
的 -子半群,且同构于
-子半群,且同构于 。
。
定理3.6:令 为幂等元连接富足半群。若
为幂等元连接富足半群。若 的所有正则元构成子半群,则
的所有正则元构成子半群,则 为超富足半群当且仅当
为超富足半群当且仅当
(1) 的每个
的每个 -类构成子半群;
-类构成子半群;
(2) ;
;
(3) 不含同构于
不含同构于 或
或 的
的 -子半群。
-子半群。
证明:为证必要性,仅需证:当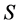 为超富足半群时,条件(3)满足。现设
为超富足半群时,条件(3)满足。现设 为半群
为半群 分解成完全
分解成完全 -单半群
-单半群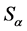 的半格分解。反设,
的半格分解。反设, 含有同构于
含有同构于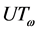 的子半群
的子半群 。令
。令 ,则
,则 可以比较,但每个
可以比较,但每个 都是完全
都是完全 -单半群,于是
-单半群,于是 属于不同的
属于不同的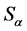 。无妨设
。无妨设 且
且 ,那么
,那么 。由于
。由于 ,必有
,必有 使得
使得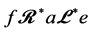 ,从而
,从而 应该属于同一个
应该属于同一个 -类。但每一个
-类。但每一个 事实上为一个
事实上为一个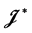 -类,所以
-类,所以 ,矛盾。故条件(3)成立。
,矛盾。故条件(3)成立。
反过来,设条件(1),(2),(3)成立,那么 的每一个
的每一个 -类构成
-类构成 的
的 -子半群,且满足
-子半群,且满足
·  -单的;
-单的;
· 所有正则元构成子半群;
· 为幂等元连接的。
据引理3.4,3.5和条件(3),知 的每个
的每个 -类中的幂等元不可比较,从而
-类中的幂等元不可比较,从而 的每个
的每个 -类中的幂等元都是本原的,再据([2] , Corollary 5.2),
-类中的幂等元都是本原的,再据([2] , Corollary 5.2), 的每个
的每个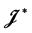 -类是完全
-类是完全 -单半群。利用定理2.3,可得
-单半群。利用定理2.3,可得 为超富足半群。
为超富足半群。
对偶地,可得
定理3.7:令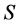 为幂等元连接富足半群。若
为幂等元连接富足半群。若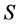 的所有正则元构成子半群,则
的所有正则元构成子半群,则 为超富足半群当且仅当
为超富足半群当且仅当
(1) 的每个
的每个 -类构成子半群;
-类构成子半群;
(2) ;
;
(3) 不含同构于
不含同构于 或
或 的
的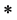 -子半群。
-子半群。
基金项目
国家自然科学基金(11361027),江西省自然科学基金和江西省教育厅科研基金资助项目。
文章引用
侯永林,郭文娟,郭小江, (2015) 超富足半群的若干特征
Characterizations of Superabundant Semigroups. 理论数学,02,66-72. doi: 10.12677/PM.2015.52010
参考文献 (References)
- 1. Fountain, J.B. (1979) Adequate semigroups. Proceedings of the Edinburgh Mathematical Society, 22, 113-125.
- 2. Fountain, J.B. (1982) Abundant semigroups. Proceedings London Mathematical Society, 44, 103-129.
- 3. 何晓婷, 郭小江 (2014), 完全 -单半群的若干特征. 理论数学, 4, 1-4.
- 4. Petrich, M. and Reilly, N.R. (1999) Completely regular semigroups. John Wiley & Sons, INC., New York, Chichester, Weinheim, Brisbane, Singapore, Toronto.
- 5. Clifford, A.H. and Preston, G.B. (1961) The algebraic theory of semigroups, Vol. I, Mathematical Survey. American Mathematical Society, Provindence, 7.
- 6. Howie, J.M. (1976) An intro-duction to semigroup theory. Academic Press, London.
- 7. Fountain, J.B. and Gould, V. (2004) Endomorphisms of relatively free algebras with weak exchange properties. Algebra Universalis, 51, 257-285.
- 8. Guo, X.J. and Luo, Y.F. (2005) The natural orders on abundant semigroups. Advances in Mathematics (China), 34, 297-308.
- 9. Guo, X.J., Guo, Y.Q. and Shum, K.P. (2010) Super rpp semigroups. Indian Journal of Pure and Applied Mathematics, 41, 505-533.