Pure Mathematics
Vol.07 No.01(2017), Article ID:19583,7
pages
10.12677/PM.2017.71007
Two Weak Endpoint Estimates on Bilinear Hardy Operators
Chunmei Zhang
School of Mathematics & Computer Science, Anhui Normal University, Wuhu Anhui

Received: Jan. 3rd, 2017; accepted: Jan. 19th, 2017; published: Jan. 22nd, 2017
Copyright © 2017 by author and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
By strict calculation, we mainly give the weak estimate for the boundary of the bilinear Hardy operator on the Morrey space and the weighted Lebesgue space, which is a useful supplement to the existing theory.
Keywords:Hardy Operator, Multiple Hardy Operator, Lp Space, Morrey Space

关于双线性Hardy算子的 两个端点弱型估计
张春梅
安徽师范大学数学与计算机科学学院,安徽 芜湖

收稿日期:2017年1月3日;录用日期:2017年1月19日;发布日期:2017年1月22日

摘 要
通过严格的计算,对双线性Hardy算子在中心Morrey空间和加权Lebesgue空间上的边界进行了端点情形下的弱型估计,这是对现有理论的有益补充。
关键词 :Hardy算子,双线性Hardy算子,Lp空间,Morrey空间

1. 引言和主要结果
对于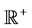 上的局部可积函数f,经典的Hardy算子定义为
上的局部可积函数f,经典的Hardy算子定义为
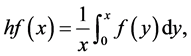
它满足如下积分不等式:
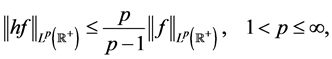
这里的常数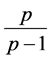 是最优的。关于Hardy算子的其他经典结果及最新的一些进展可见文献 [1] - [18] ,本文拟将已知的一些关于高维Hardy算子的结果推广到多线性情形。
是最优的。关于Hardy算子的其他经典结果及最新的一些进展可见文献 [1] - [18] ,本文拟将已知的一些关于高维Hardy算子的结果推广到多线性情形。
为叙述方便,我们引入一些定义和记号。对于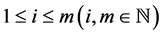 ,
,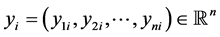 ,记每个yi的欧氏范数为
,记每个yi的欧氏范数为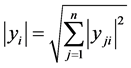 ,m元数组
,m元数组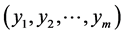 的欧氏范数为
的欧氏范数为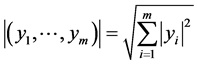 ;同时,我们用
;同时,我们用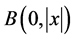 表示
表示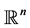 上的以原点为中心,|x|为半径的球体,用
上的以原点为中心,|x|为半径的球体,用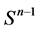 表示n维单位球面,用
表示n维单位球面,用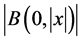 和
和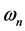 分别表示
分别表示 和
和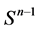 的外测度,特别地,用
的外测度,特别地,用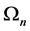 表示
表示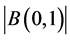 ;对于
;对于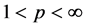 ,我们用p'表示p的共轭指数,即
,我们用p'表示p的共轭指数,即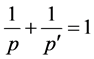 。
。
设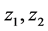 是实部为正的复数,记Gamma函数为
是实部为正的复数,记Gamma函数为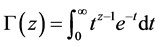 。则
。则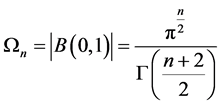 。
。
定义1.1:设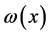 是
是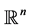 上的一个非负局部可积函数,如果
上的一个非负局部可积函数,如果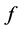 满足
满足
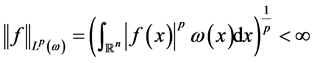
则称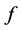 为加权
为加权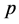 次可积函数,记作
次可积函数,记作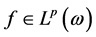 。
。
如果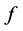 满足
满足
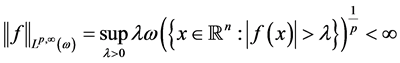
则称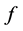 为广义加权
为广义加权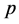 次可积函数,记作
次可积函数,记作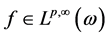 。
。
其中,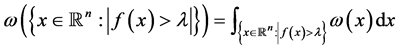 。而
。而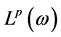 ,
,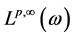 分别为加权
分别为加权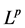 空间和加权弱型
空间和加权弱型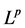 空间。
空间。
定义1.2:设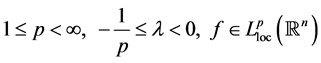 ,称
,称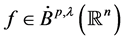 ,如果
,如果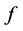 满足
满足
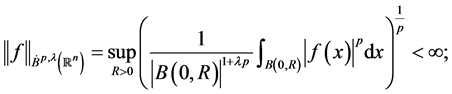
称函数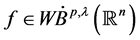 ,如果
,如果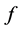 满足
满足
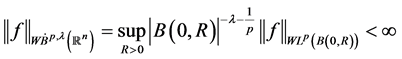
其中,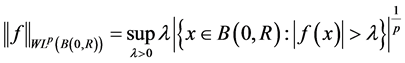 。
。
这里,我们称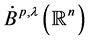 ,
,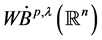 分别为
分别为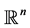 上的中心Morrey空间和中心弱型Morrey空间。
上的中心Morrey空间和中心弱型Morrey空间。
历史上,在1995年,Christ和Grafakos [19] 引入了n维Hardy算子
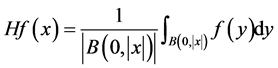
并得到了如下形式的Hardy不等式
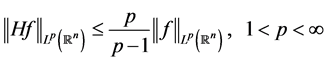 。
。
Fu Z [20] 等研究了双线性函数的Hardy算子
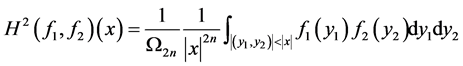 。
。
他们得到了如下结论:
(1) [20] 设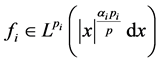 ,
,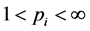 ,
,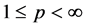
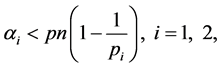 ,
,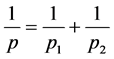 ,且
,且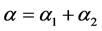 。那么,
。那么,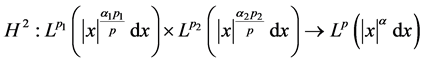 是有界的,且其算子范数为
是有界的,且其算子范数为
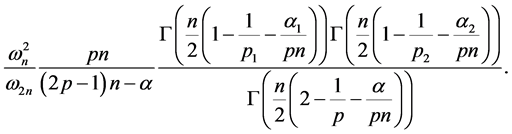
(2) [20] 设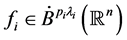 ,
,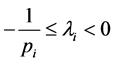 ,i = 1, 2,
,i = 1, 2,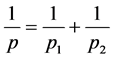 ,
,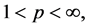 且
且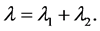 则
则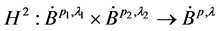 是有界的,且其算子范数为
是有界的,且其算子范数为
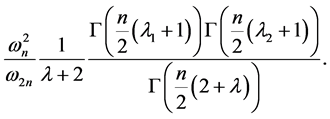
最近,Long R L [13] ,Xiao J [14] ,Gao G,Zhao F [21] 等研究了n维Hardy算子的弱型估计,并得到了如下的结果:
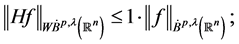
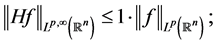
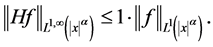
其中,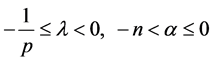
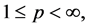 。
。
受以上文章的启发,本文试图考虑多线性Hardy算子在加权Lebesgue空间和Morrey空间上的弱型估计。需要指出的是,本文的方法不同于Gao G [13] 等的研究方法。我们的结果如下:
定理1.1:设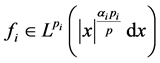 ,
,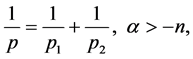
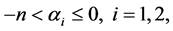
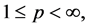
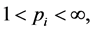 且
且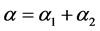 。那么,
。那么,
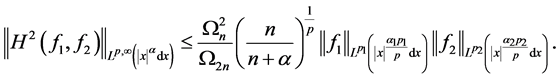
注记:令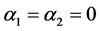 ,则有
,则有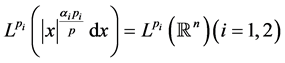 ,
,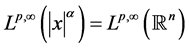 ,因此定理1.1蕴含了下面的不等式也是成立的,
,因此定理1.1蕴含了下面的不等式也是成立的,
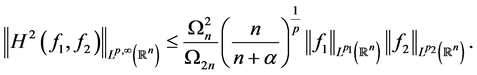
定理1.2:设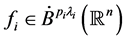 ,
,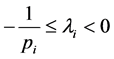 ,i = 1, 2,
,i = 1, 2,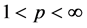 ,
,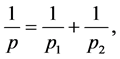 且
且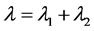 。那么
。那么
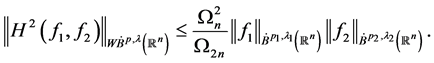
2. 主要结果的证明
首先,对于加幂权Lebesgue空间,我们证明了其乘积空间到弱型空间的Hardy算子范数是有界的。
定理1.1的证明:
易见,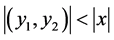 蕴含了
蕴含了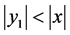 ,
,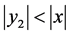 ,从而,利用
,从而,利用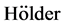 不等式,我们有如下的点态估计,
不等式,我们有如下的点态估计,
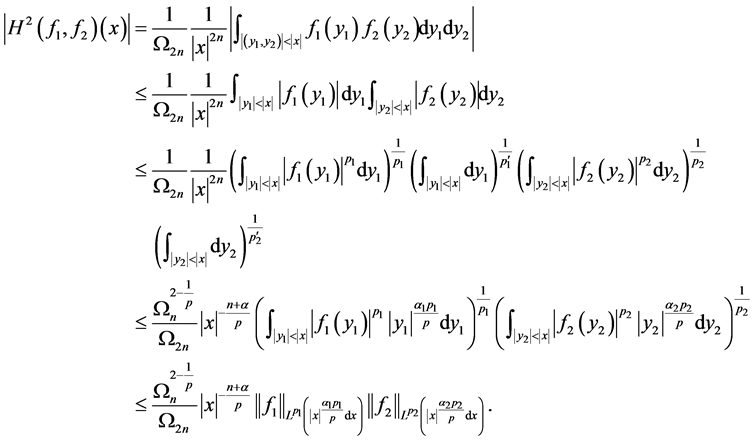
令
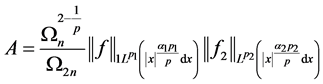 ,
,
由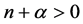 可得
可得
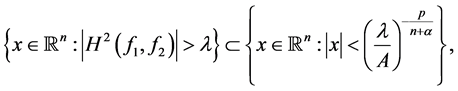
因此,
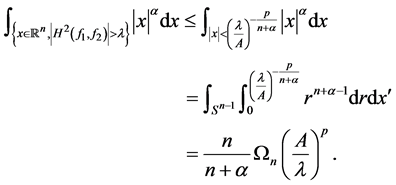
从而,
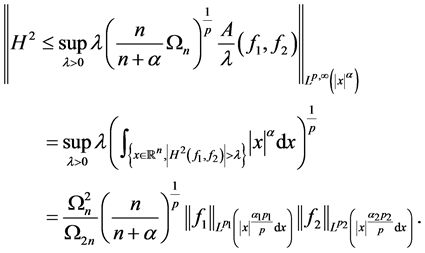
其次,对于Morrey空间,我们也证明了其乘积空间到弱型空间的Hardy算子范数是有界的。
定理1.2的证明:
类似于定理1.2的证明,由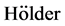 不等式,我们有如下点态估计,
不等式,我们有如下点态估计,
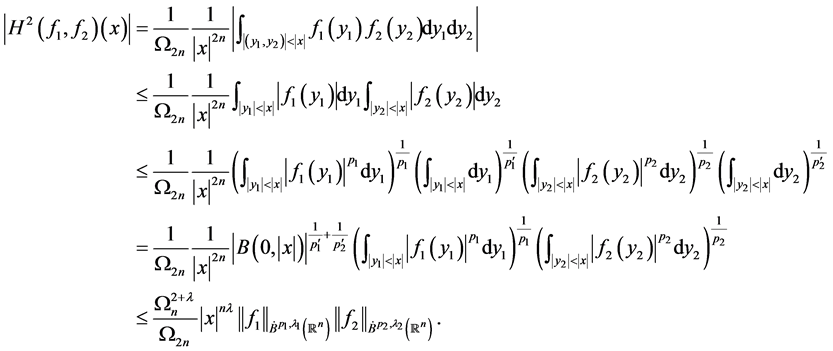
令
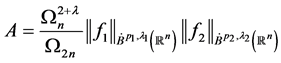 ,
,
由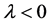 可以得到
可以得到
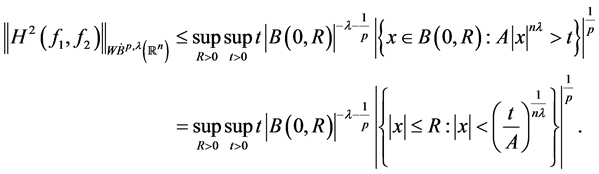
若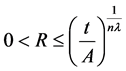 ,那么,因为
,那么,因为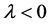 ,从而
,从而
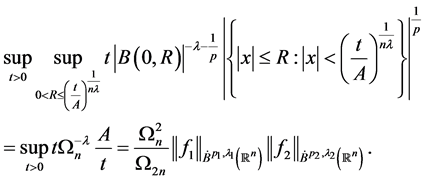
若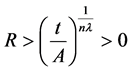 ,由
,由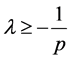 可得
可得
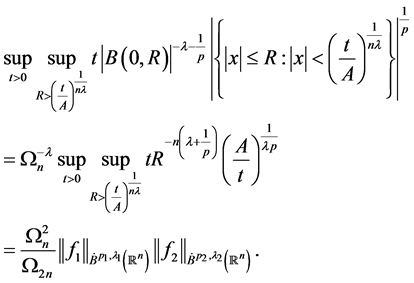
从而有
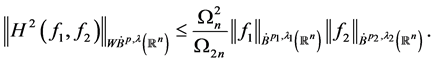
致谢
本文的写作感谢瞿萌老师指导!
基金项目
安徽师范大学本科生优秀毕业论文(设计、创作)培育计划项目资助。
文章引用
张春梅. 关于双线性Hardy算子的两个端点弱型估计
Two Weak Endpoint Estimates on Bilinear Hardy Operators[J]. 理论数学, 2017, 07(01): 43-49. http://dx.doi.org/10.12677/PM.2017.71007
参考文献 (References)
- 1. Anderson, K. and Muckenhoupt, B. (1982) Weighted Weak Type Hardy Inequalities with Application to Hilbert Transforms and Maximal Functions. Studia Mathematica, 72, 9-26.
- 2. Chen, J.C., Fan, D.S. and Wang, S.L. (2013) Hausdorff Operators on Euclidean Spaces. Applied Mathematics—A Journal of Chinese Universities, 28, 548-564. https://doi.org/10.1007/s11766-013-3228-1
- 3. Bennet, C., Devore, R.A. and Sharpley, R.C. (1981) Weak and BMO. Annals of Mathematics, 113, 601-611. https://doi.org/10.2307/2006999
- 4. Bliss, G.A. (1930) An Integral Inequality. Journal London Mathematical Society, 317, 40-46. https://doi.org/10.1112/jlms/s1-5.1.40
- 5. Broadbent, T.A.A. (1928) A Proof of Hardy’s Convergence Theorem. Journal London Mathematical Society, 3, 242- 243. https://doi.org/10.1112/jlms/s1-3.4.242
- 6. Levinson, N. (1964) Generalizations of an Inequality of Hardy. Duke Mathematical Journal, 31, 389-394. https://doi.org/10.1215/S0012-7094-64-03137-0
- 7. Muckenhoupt, B. (1972) Hardy’s Inequality with Weights. Studia Mathematica, 44, 31-38.
- 8. Golubov, B.I. (1997) Boundedness of the Hardy and the Hardy-Littlewood Operators in the Spaces ReH1 and BMO. Sbornik: Mathematics, 188, 1041-1054. https://doi.org/10.1070/SM1997v188n07ABEH000246
- 9. Rakotondratsimba, Y. (1998) On the Boundedness of Classical Operators on Weighted Lorentz Spaces. Georgian Mathematical Journal, 5, 177-200. https://doi.org/10.1007/BF02767995
- 10. Calderon, A.P. (1966) Space between and and the Theorem of Marcikiewiez. Studia Mathematica, 26, 273- 299.
- 11. Hardy, G.H. (1928) Note on Some Points in the Integral Calculus. Messenger of Mathematics, 57, 12-16.
- 12. Martin-Reyes, F. and Ortega, P. (1998) On Weighted Weak Type Inequalities for Modified Hardy Operators. Proceedings of the American Mathematical Society, 126, 1739-1746. https://doi.org/10.1090/S0002-9939-98-04247-6
- 13. Long, R.L. (1985) Hp Martingale Theory. Peking University Press, Beijing.
- 14. Xiao, J. (2001) and BMO Bounds of Weighted Hardy-Littlewood Averages. Journal of Mathematical Analysis and Applications, 262, 660-666. https://doi.org/10.1006/jmaa.2001.7594
- 15. Hardy, G.H., Littlewood, J.E. and Polya, G. (1934) Inequalities. Cambridge University Press, London and New York.
- 16. Edmunds, D., Gurka, P. and Pick, L. (1994) Compactness of Hardy Type Operators in Weighted Banach Function Spaces. Studia Mathematica, 109, 73-90.
- 17. Christ, M. and Grafakos, L. (1995) Best Constants for Two Non-Convolution Inequalities. Proceedings of the American Mathematical Society, 123, 1687-1687. https://doi.org/10.1090/S0002-9939-1995-1239796-6
- 18. Gao, G., Hu, X. and Zhang, C. (2016) Sharp Weak Estimates for Hardy-Type Operators. Annals of Functional Analysis, 7, 421-433. https://doi.org/10.1215/20088752-3605447
- 19. Zhao, F.Y., Fu, Z.W. and Lu, S.Z. (2012) Endpoint Estimates for n-Dimensional Hardy Operators and Their Commutators. Science China Mathematics, 55, 1977-1990. https://doi.org/10.1007/s11425-012-4465-0
- 20. Fu, Z., Grafakos, L., Lu, S.Z., et al. (2012) Sharp Bounds for m-Linear Hardy and Hilbert Operators. Houston Journal of Mathematics, 38, 225-244.
- 21. Gao, G. and Zhao, F. (2015) Sharp Weak Bounds for Hausdorff Operators. Analysis Mathematica, 41, 163-173. https://doi.org/10.1007/s10476-015-0204-4