Optoelectronics
Vol.
09
No.
01
(
2019
), Article ID:
29432
,
6
pages
10.12677/OE.2019.91007
Dipole Mode of Plasmon in Finite-Size Simple Cubic Lattice System of Tight-Binding Model
Renglai Wu*, Jun Quan, Shifa Xiao
College of Physics Science and Technology, Lingnan Normal University, Zhanjiang Guangdong

Received: Mar. 5th, 2019; accepted: Mar. 19th, 2019; published: Mar. 26th, 2019

ABSTRACT
Based on the tight-binding model, we developed the linear response theory to construct the dipole response function of finite-size simple cubic lattice systems. Through the change of dipole response function with the frequency of external electric potential field, we pointed out that when the dipole mode of the plasmon in a simple cubic lattice is excited by an external field, the real part of the dipole response function will be reversed and the imaginary part of the dipole response function will be maximized. These results imply that the energy absorbed by the system from the external potential field is extremely high at dipole plasmon, and the energy absorption is accomplished by the violently dipole moment oscillations. Furthermore, we show that the charge of the system will show dipole moment characteristics in different directions at dipole plasmon.
Keywords:Simple Cubic Lattice, Plasmon, The Linear Response Theory, The Tight-Binding Mode
紧束缚模型下有限尺寸的简立方晶格体系等离激元的偶极模式
吴仍来*,全军,肖世发
岭南师范学院物理科学与技术学院,广东 湛江

收稿日期:2019年3月5日;录用日期:2019年3月19日;发布日期:2019年3月26日

摘 要
基于紧束缚模型,发展了线性响应理论构造了有限尺寸的简立方晶格体系的偶极响应函数。通过偶极响应函数随外加电势场频率的变化关系,指出简立方晶格体系等离激元的偶极模式被外场激发时,偶极响应函数的实部会出现反转,偶极响应函数的虚部会出现极大值。这些结果意味着等离激元的偶极模式被激发时,体系对外加电势场的能量吸收有极大值,能量吸收的同时伴随偶极矩的剧烈振荡。进一步,我们给出在偶极等离激元处体系的电荷会在各个不同方向显示出偶极矩特征。
关键词 :简立方晶格,等离激元,线性响应理论,紧束缚模型

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
扫描隧道显微镜(STM)的进展显示通过STM的探针可操纵单个原子,实现对原子团簇和分子的形状、结构和尺寸的精确控制 [1] [2] [3] 。这极大地激发了人们对少数原子体系物理、化学和光电性质的研究热情,期望能发现新的物理、化学和光电特性。在少数原子体系光电性质的研究中,等离激元占据比较大的比重。过去数十年中,一系列理论计算和实验结果都报道了少数原子体系等离激元的存在 [4] - [9] 。等离激元是电子或等离子体的集体激发模式,由外加电磁场和电子或等离子体耦合形成,一般发生在金属和半导体结构。局域的等离激元所具有的局域光波导、电荷累积、电场增强和电场强束缚等特性,推动了等离激元在生物、化学、材料、能源等方面的开发和利用 [10] [11],加速了现代科技产业的转型。以等离激元为基础的科技产品如今已被广泛应用于共振传感器 [12],光开关器件 [13],光逻辑运算 [14],激光器件 [15] 等方面。这些应用成果意味着等离激元的研究在新产品新技术的前沿领域具有重大的影响力,潜移默化地引导着新兴科技的发展。最近几年,伴随着科学界对超材料、变换光学等相关领域的深入探索,等离激元的研究也得到了进一步的拓展,尤其是等离激元的偶极模式获得了极大的关注 [16] 。人们在寻求能够对等离激元的偶极模式进行有效研究的普适理论和方法 [16] 。
最近,通过标准的线性响应理论,我们在一维和二维体系中研究了偶极模式的等离激元(简称偶极等离激元) [6] [7] [8] [9],利用偶极响应函数得到的研究结果和其它文献的结果吻合得很好 [4] [5] 。本文中,我们把偶极响应函数方法推广到有限尺寸的简立方晶格体系。基于紧束缚模型,本文给出了偶极响应函数来寻找简立方晶格体系等离激元的偶极模式,研究了偶极等离激元激发时简立方晶格体系电荷的分布特征。
2. 模型和研究方法
简立方晶格的模型图如图1所示,模型中只考虑最近邻格点对电子的库伦作用,U表示本格点对电子的库伦作用能的大小,V表示临近格点对电子的库伦作用能的大小。接下来,用Nx,Ny和Nz来描述有限尺寸的简立方晶格在x,y和z方向上的原子数,任意格点的坐标用 来表示, ,lx、ly、lz分别为格点的x、y、z轴坐标,ex、ey、ez分别为x、y、z轴方向上的单位矢量。

Figure 1. The model of simple cubic lattice
图1. 简立方晶格的模型
在频谱空间,紧束缚模型下简立方晶格体系的哈密顿量为 [9]
(1)
式中,h.c.表示
复共轭,
为跃迁矩阵元,
和
分别为产生和湮灭算符,
为外扰电势在万尼尔表象下的表示,
。
为电荷数响应,满足
,
为无外扰时电荷数的平均值,由于
与体系的动力学性质无关,可被忽略。
,
和 分别是方晶格体系电子的本征函数和本征能量,无外加扰动时,基于哈密顿量的本征方程求解易得
分别是方晶格体系电子的本征函数和本征能量,无外加扰动时,基于哈密顿量的本征方程求解易得
(2)
(3)
(2)和(3)式中, , , , , , 。基于标准的线性响应理论,电荷数对外加电势的响应为
(4)
式中 为林哈德函数
(5)
其中,h为散射系数,f(En)为费米函数。(4)式简化为
(6)
式中
(7)
将响应电荷量和响应电荷数的关系 代入(6)式得
(8)
(8)式为体系电荷量对外加电势的响应方程。整理(8)式可得
(9)
当外场 的频率等于偶极等离激元的频率时,体系中的电荷发生偶极矩共振,利用(9)式求偶极响应函数
(10)
由于散射系数的存在,(10)式中偶极响应函数是个复数,接下来我们根据偶极响应函数 的实部和虚部随外加电势场频率的变化来寻找等离激元的偶极模式。
3. 计算结果
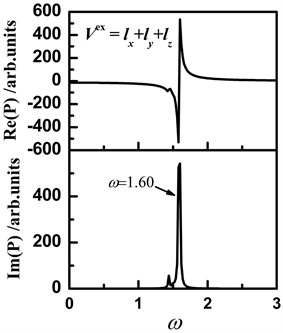
Figure 2. The dipole response function varies with the frequency of the external electrical potential
图2. 偶极响应函数随外加电势频率的变化
图2中简立方晶格的尺寸为 , ,计算参数取U = 3.0 eV,V = 1.0 eV,h = 0.01 eV,等离激元的频率以2pg/h为基本单位,h为普朗克常量。图2(a)给出偶极响应函数的实部随外加电势频率的变化;图2(b)给出偶极响应函数的虚部随外加电势频率的变化。其中,偶极响应函数的实部代表实际的偶极矩的大小,虚部代表能量吸收。该图结果显示:偶极响应函数的虚部在频率w = 1.60处出现极大值,偶极响应函数的实部在频率w = 1.60附近出现反转。表明在频率w = 1.60处简立方晶格体系对外加电势场的能量吸收最大,吸收能量的同时,偶极矩发生剧烈振荡,导致偶极响应函数的实部出现反转,体系中的电荷发生了偶极共振,由此可判断频率w = 1.60处有一个偶极模式的等离激元。
图3给出频率w = 1.60处偶极等离激元激发时,电荷在z = 0的x-y平面,y = 0的x-z平面和z = 0的y-z平面的分布特征。结果显示:在z = 0的x-y平面,正负电荷主要分别集中在体系右上角和左下角,电

Figure 3. The charge distribution at plasmon frequency w = 1.60, the system is the same as in Figure 2
图3. 等离激元频率w = 1.60处的电荷分布,体系与图2相同
荷沿着x和y方向都有明显的偶极矩特征;在y = 0的x-z平面,正负电荷主要分别集中在体系的右和左两端,电荷沿着x方向有明显的偶极特征;在z = 0的y-z平面,正电荷主要集中在体系左上角靠近中心的位置,负电荷环绕在正电荷附近,沿着x和y方向有较弱的偶极特征。不同平面上电荷分布的结果共同表明了等离激元的偶极模式被激发时,体系中的电荷将具备各个方向上的偶极矩特征,因此偶极模式被激发时,体系内部的电荷将发生剧烈的偶极振荡。本文将以往一维和二维体系等离激元的研究拓展到了实际的方晶格体系,所得偶极等离激元的激发特性与一维和二维体系偶极等离激元的激发特性类似 [4] - [9],有效的阐明了该模式的电荷极化特征。
4. 结论
基于线性响应理论和紧束缚模型,给出了偶极响应函数求解了有限尺寸简立方晶格体系等离激元的偶极模式。基于偶极响应函数的实部和虚部随外加电势场频率的变化结果,给出偶极等离激元被外场激发时,极响应函数的虚部会出现极大值,偶极响应函数的实部会出现反转。进一步给出了偶极等离激元被激发时,方晶格体系的电荷在各个不同的方向都呈现偶极矩分布特征。
基金项目
国家自然科学基金(11647156)和岭南师范学院校级项目(ZL1618)的资助课题。
文章引用
吴仍来,全 军,肖世发. 紧束缚模型下有限尺寸的简立方晶格体系等离激元的偶极模式
Dipole Mode of Plasmon in Finite-Size Simple Cubic Lattice System of Tight-Binding Model[J]. 光电子, 2019, 09(01): 42-47. https://doi.org/10.12677/OE.2019.91007
参考文献
- 1. Nilius, N., Wallis, T.M. and Ho, W. (2002) Development of One-Dimensional Band Structure in Artificial Gold Chains. Science, 297, 1853-1856. https://doi.org/10.1126/science.1075242
- 2. Nazin, G.V., Qiu, X.H. and Ho, W. (2003) Atomic Engineering of Photon Emission with a Scanning Tunneling Microscope. Physical Review Letters, 90, Article ID: 216110. https://doi.org/10.1103/PhysRevLett.90.216110
- 3. Nayyar, N., Turkowski, V. and Rahman, T.S. (2012) Optical Generation of Collective Plasmon Modes in Small Gold Chains Induced by Doping Transition-Metal Impurities. Physical Review Letters, 109, Article ID: 157404. https://doi.org/10.1103/PhysRevLett.109.157404
- 4. Yuan, Z. and Gao, S. (2008) Plasmon Resonances in Linear Atomic Chains: Free-Electron Behavior and Anisotropic Screening of D’Electrons. Physical Review B, 78, Article ID: 235413. https://doi.org/10.1103/PhysRevB.78.235413
- 5. Yan, J., Yuan, Z. and Gao, S. (2007) End and Central Plasmon Resonances in Linear Atomic Chains. Physical Review Letters, 98, Article ID: 216602. https://doi.org/10.1103/PhysRevLett.98.216602
- 6. Wu, R., Xue, H., Yu, Y., Hu, H. and Liu, Q. (2014) Quadrupole Plasmon Excitations in Confined One-Dimensional Systems. Europhysics Letters, 108, 27001-27005. https://doi.org/10.1209/0295-5075/108/27001
- 7. Wu, R., Xue, H., Yu, Y. and Hu, H. (2014) Dipole and Quadrupole Plasmon in Confined Quasi-One-Dimensional Electron Gas Systems. Physics Letters A, 378, 2995-3000. https://doi.org/10.1016/j.physleta.2014.08.013
- 8. Xue, H.J., Wu, R.L. and Hu, C.X. (2018) The Study of the Plasmon Modes of Square Atomic Clusters Based on the Eigen-Oscillation Equation of Charge under the Free-Electron Gas Model. International Journal of Modern Physics B, 32, Article ID: 1850139. https://doi.org/10.1142/S0217979218501394
- 9. 吴仍来, 肖世发, 薛红杰, 等. 二维方形量子点体系等离激元的量子化[J]. 物理学报, 2017(66): 266-272.
- 10. 王振林. 表面等离激元研究新进展[J]. 物理学进展, 2009, 29(3): 287-324.
- 11. 童廉明, 徐红星. 表面等离激元——机理、应用与展望[J]. 物理, 2012, 41(9): 582-588. http://www.wuli.ac.cn/CN/Y2012/V41/I9/582
- 12. Larsson, E.M., Langhammer, C., ZoricIetal, I. and Bengt, K. (2009) Nanoplasmonic Probes of Catalytic Reactions. Science, 326, 1091-1094. https://doi.org/10.1126/science.1176593
- 13. Pacifici, D., Lezec, H.J. and Atwater, H.A. (2007) All-Optical Modulation by Plasmonic Excitation of CdSe Quantum Dots. Nature Photonics, 1, 402-406. https://doi.org/10.1038/nphoton.2007.95
- 14. Wei, H., Li, Z.P., Tian, X.R., et al. (2011) Quantum Dot-Based Local Field Imaging Reveals Plasmon-Based Interferometric Logic in Silver Nanowire Networks. NanoLetters, 11, 471. https://doi.org/10.1021/nl103228b
- 15. Wan, Y.T., Norman, J., Li, Q., et al. (2017) 1.3 μm Submilliamp Threshold Quantum Dot Micro-Lasers on Si. Optica, 4, 940-944. https://doi.org/10.1364/OPTICA.4.000940
- 16. Maier, M., Margetis, D. and Luskin, M. (2017) Dipole Excitation of Surface Plasmon on a Conducting Sheet: Finite Element Approximation and Validation. Journal of Computational Physics, 339, 126-145. https://doi.org/10.1016/j.jcp.2017.03.014
NOTES
*通讯作者。