Modeling and Simulation
Vol.05 No.04(2016), Article ID:19100,9
pages
10.12677/MOS.2016.54021
Research on Protfolio Investment Optimization Based on Genetic-Ant Colony Algorithm
Huiying Wang1, Menghan Yi2, Hao Liu3
1School of Statistics and Mathematics, Central University of Finance and Economics, Beijing
2College of Science, Northeast Agricultural University, Harbin Heilongjiang
3School of Management Science and Engineering, Central University of Finance and Economics, Beijing

Received: Nov. 7th, 2016; accepted: Nov. 26th, 2016; published: Nov. 29th, 2016
Copyright © 2016 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
Based on the Markowitz portfolio theory, the multi-objective programming model of portfolio investment is established when considering the risk and return of portfolio investment. The genetic algorithm and ant colony algorithm are combined and applied to solve the above model. In detail, the initial solution of problems which is generated by the genetic algorithm with fast global searching ability is transformed into the initial information distribution of the ant colony algorithm. And then we carry on the genetic operation to the ant colony. Finally, we use the ant colony algorithm parallelism, positive feedback mechanism and the solution efficiency high characteristic to seek the optimal solution. Experiments show that: the fusion of the two algorithms has better behaviors on the quality and efficiency than separate genetic algorithm or ant colony algorithm.
Keywords:Portfolio Investment, Multi-Objective Programming, Genetic Algorithm, Ant Colony Algorithm, Algorithm Fusion

基于遗传–蚁群算法的证券组合投资优化研究
王慧颖1,衣梦涵2,刘昊3
1中央财经大学统计与数学学院,北京
2东北农业大学理学院,黑龙江 哈尔滨
3中央财经大学管理科学与工程学院,北京

收稿日期:2016年11月7日;录用日期:2016年11月26日;发布日期:2016年11月29日

摘 要
基于Markowitz资产组合理论,综合考虑证券投资的风险和收益,建立证券组合投资的多目标规划模型,融合遗传算法和蚁群算法应用于上述模型的求解。具体地,将具有快速全局搜索能力的遗传算法产生的问题初始解转化为蚁群算法的初始信息分布,再对蚁群进行遗传操作,最后利用蚁群算法的并行性、正反馈机制、求解效率高的特征寻求最优解。实验结果表明:上述两种算法的融合在求解质量和效率上均优于单独的遗传算法或蚁群算法。
关键词 :证券组合投资,多目标规划,遗传算法,蚁群算法,算法融合

1. 引言
随着我国市场经济体制的建立和完善,证券市场充满了生机和活力,也充满了困惑与风险。恰当的证券组合投资不仅可以回避风险保住资金成本,还能获得理想的收益。长期以来,投资者的决策多依赖于实验中的经验,尚未上升到理论高度。1952年,Markowitz提出了确定证券收益和风险水平的主要原理和方法,这标志着现代组合投资理论的开端 [1] 。随后,众多学者对其进行了扩展,提供了许多求解证券组合问题的有效方法 [2] 。但如何使证券组合模型成为最优化的决策模型仍亟待解决。近年来,随着人工智能技术的发展,将其应用于组合投资问题已成为更广阔的研究领域。但组合投资问题的规模和复杂度越来越大,单一算法的优化结果往往不够理想。基于这一现状,本文利用算法融合的思想提高算法优化性能。具体地,将遗传算法和蚁群算法融合求解证券组合模型最优解问题,并通过数值实验说明融合算法应用于模型求解的准确性与有效性。
1975年,美国密执安大学的Holland教授基于达尔文的进化论和孟德尔的遗传学说首次提出了遗传算法 [3] [4] 。随后De Jong将遗传算法转化为机器语言,并由Goldberg总结验证形成了官方的遗传算法 [5] 。该算法一经提出,便被广泛应用于机器学习、模式识别、神经网络、图像处理等各个领域。蚁群算法(ACO)顾名思义是受到蚂蚁群体觅食行为的启发产生的一种算法,自1991年Dorigo首次提出ACO算法后,便引起了国内外学者的广泛关注 [6] [7] 。其变异模型也被广泛应用到TSP问题、二次分配问题、Bayesian网学习问题等各类领域。
将遗传算法和蚁群算法融合,汲取两种算法的优点,克服各自的缺点,使得结合后的算法在时间和求解效率上得到改善,被称之为遗传–蚁群算法。肖宏峰等人针对连续域优化问题提出了两种融合方法,一种是利用遗传算法的全局搜索性为蚁群算法提供初始信息分布,再利用基本蚁群算法进行寻优;另一种是在基本蚁群算法寻优的过程中,为避免算法过早地陷入局部最优情况,引入遗传算法中的交叉操作来产生蚁群算法寻优的新路径,从而提高蚁群算法的全局搜索能力以获得更优解集 [8] 。
然而,遗传算法虽具有快速全局搜索能力,但未利用系统中的反馈信息,从而增加了迭代次数,导致计算效率低。蚁群算法通过信息素累计和更新收敛于最优路径,具有并行、分布、全局收敛能力,但搜索初期信息素匮乏使得搜索初期信息素累计时间过长,导致求解速度慢 [9] 。为克服遗传算法和蚁群算法的缺陷,形成优势互补,本文利用遗传算法的随机搜索、快速、全局收敛性产生问题的初始解,将其转化为蚁群算法的初始信息分布,再利用蚁群算法的并行性、正反馈机制、求解效率高的特征寻求最优解。在蚁群算法求解过程中,每个蚂蚁都具有普通生物体共有的生物特征,因此本文将遗传机理赋予智能蚂蚁,每个蚂蚁又受制于遗传算法的调节,使得蚁群算法无论从个体上还是整体上得到改进,从而得到一种新的遗传–蚁群算法。最后,将该融合算法应用于证券组合投资实例中,实验结果表明:无论是在求解时间效率方面还是在求得解的稳定性方面,融合算法均优于单一的遗传或蚁群算法。
2. 证券组合投资优化问题及其数学模型
在证券市场中,投资者会争相购买收益率较高风险较低的证券,当证券收益降到一定程度或者风险升高到一定程度时,投资者会转而去购买别的证券。这种行为类似于自然界的适者生存原则和蚂蚁的觅食行为,受此启发本文将遗传算法和蚁群算法应用到证券市场投资者行为的模拟中,寻找最优的证券投资组合。
假设市场中有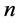 种证券待投资,记第
种证券待投资,记第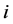 种证券的期望收益率为
种证券的期望收益率为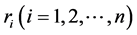 。由于
。由于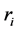 受证券市场中的各种因素影响,故将其看成随机变量。记
受证券市场中的各种因素影响,故将其看成随机变量。记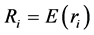 为
为 的均值,
的均值, 为
为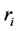 的方差,
的方差,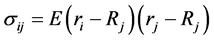 为第
为第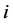 个证券与第
个证券与第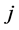 个证券的协方差,
个证券的协方差,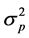 为证券组合投资的风险,
为证券组合投资的风险,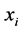 为第
为第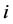 个证券被投资的比例,满足关系式
个证券被投资的比例,满足关系式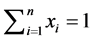 ,则证券组合投资的期望收益率为
,则证券组合投资的期望收益率为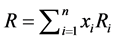 ,其方差为
,其方差为
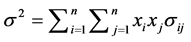 ,故证券组合的多目标规划模型为
,故证券组合的多目标规划模型为
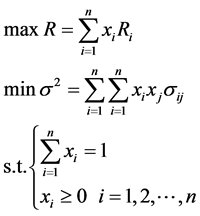 (1)
(1)
在(1)式的限制条件中,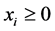 意为我国不允许卖空证券。
意为我国不允许卖空证券。
记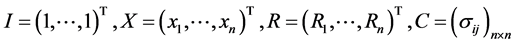 为对称正定矩阵即协方差矩阵。若考虑最小交易单位的限制,记
为对称正定矩阵即协方差矩阵。若考虑最小交易单位的限制,记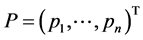 为第
为第 个证券每手交易的市场价格,
个证券每手交易的市场价格,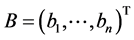 为可投资金额上限,则(1)式等价为:
为可投资金额上限,则(1)式等价为:
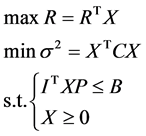 (2)
(2)
即
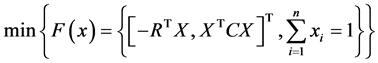 (3)
(3)
(3)式即为既能提高收益又能降低风险的多目标决策模型。
多目标优化的解法层出不穷,但其基本思想均是把多目标问题转化为单目标问题,再利用较为成熟的单目标优化方法求得最优解。各种解法可分为两类:一类是针对多目标函数的一个分量进行优化,而把其它的分量作为约束条件,或者构造一个序列单目标优化;另一类是把多目标函数的各分量按照一定规则构成一个评价函数,并把该评价函数作为单目标进行优化求解。本文采用多目标规划的模糊优选法,将收益—风险转化为单目标规划模型:
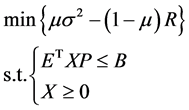 (4)
(4)
这里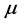 为厌恶系数,其取值范围为
为厌恶系数,其取值范围为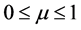 ,
,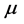 越大说明投资者越不能接受投资风险,当
越大说明投资者越不能接受投资风险,当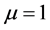 时表明投资者完全规避风险。
时表明投资者完全规避风险。
3. 遗传–蚁群算法求解证券组合投资优化问题
3.1. 遗传–蚁群算法设计
3.1.1. 编码方式及种群初始化
本节将融合算法应用于证券组合投资优化问题的求解。具体地,利用遗传算法提供蚁群初始信息,再引入遗传算法的交叉运算产生蚁群算法寻优途径。注意到遗传算法的运行动态确定了两种算法的融合时机,而选择合适的节点使用融合算法可以避免遗传算法过早或过晚结束对算法整体性能的不良影响,因此融合算法是提高时间和求解效率的启发式算法。图1为遗传–蚁群算法的总体流程图。
记整数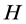 为染色体个数,随机产生
为染色体个数,随机产生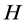 个初始染色体,这里采用整数编码 [10] ,每个染色体含
个初始染色体,这里采用整数编码 [10] ,每个染色体含 个基因位(
个基因位(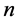 只证券),基因的数值代表证券在组合投资中的投资股数,再随机产生0~1之间的随机数。若此基因位于染色体第
只证券),基因的数值代表证券在组合投资中的投资股数,再随机产生0~1之间的随机数。若此基因位于染色体第 个位置(第
个位置(第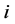 个证券),则此基因的值如下:
个证券),则此基因的值如下:
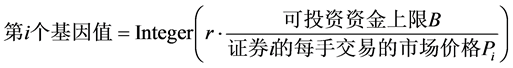 (5)
(5)
其中 表示不超过
表示不超过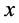 的最大整数。
的最大整数。
初始化后再将每条染色体可行化,使各个基因值都满足(4)式中的限制条件,为使染色体上的基因满足限制式 ,将染色体上的各基因
,将染色体上的各基因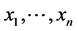 分别除以
分别除以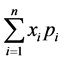 ,小数部分取小于等于基因值的最小整数。经过有限次抽样,得到
,小数部分取小于等于基因值的最小整数。经过有限次抽样,得到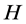 个初始可行染色体
个初始可行染色体 。
。
3.1.2. 适应度函数
由于选择机制为轮盘赌选择法,所以适应函数应大于等于0。为此我们选择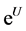 作为适应函数,其中
作为适应函数,其中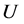 为投资组合中的目标函数式。
为投资组合中的目标函数式。
3.1.3. 选择操作(轮盘赌选择法)
1) 由于适应性强的染色体被选择产生后代的机率大,给每个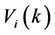 定义一个繁殖概率:
定义一个繁殖概率:
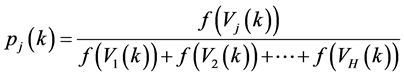 (6)
(6)
这里当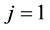 时,染色体最好,当
时,染色体最好,当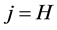 时,染色体最差。
时,染色体最差。
2) 对每个染色体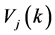 ,计算累计概率
,计算累计概率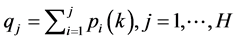 。
。
3) 产生区间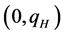 内的一个随机数
内的一个随机数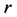 ,若
,若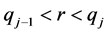 ,则选择第
,则选择第 个染色体。
个染色体。
4) 重复2),3)步共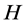 次,得到
次,得到 个复制的染色体,记为
个复制的染色体,记为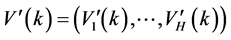 。
。
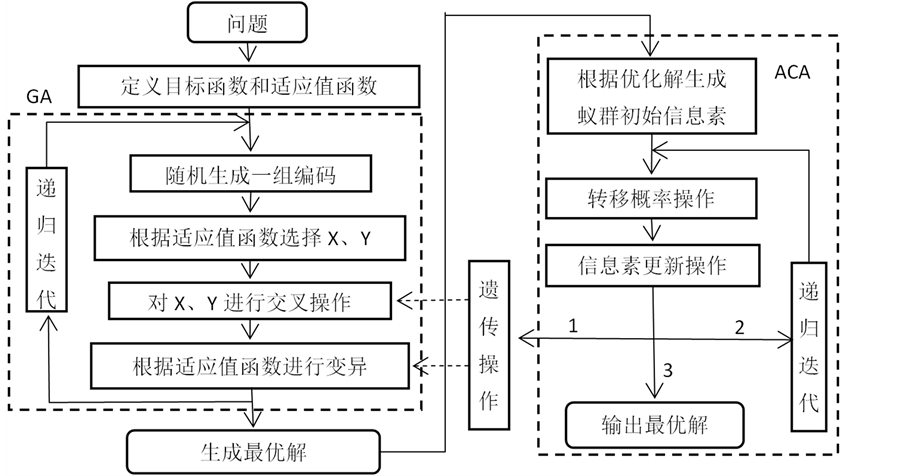
Figure 1. Flow chart of Genetic-Ant colony algorithm
图1. 遗传–蚁群算法流程图
3.1.4. 交叉和变异操作
自适应遗传算法较好地解决了动态调节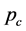 和
和 的问题,但该算法求得的解仅具有局部最优性。因此本文采用了一种改进的自适应遗传算法,称为
的问题,但该算法求得的解仅具有局部最优性。因此本文采用了一种改进的自适应遗传算法,称为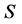 -自适应遗传算法。定义交叉概率、变异概率分别为:
-自适应遗传算法。定义交叉概率、变异概率分别为:
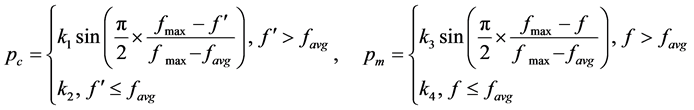 (7)
(7)
1) 交叉操作
设参数 为交叉概率,从
为交叉概率,从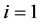 到
到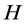 重复:产生区间
重复:产生区间 内的随机数
内的随机数 ,若
,若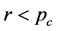 ,则染色体
,则染色体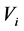 被选作父代。假设
被选作父代。假设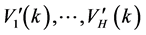 为选择的父代,对它们进行随机分对,采用单点交叉操作方法。从
为选择的父代,对它们进行随机分对,采用单点交叉操作方法。从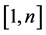 中随机产生整数
中随机产生整数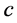 ,对每对染色体第
,对每对染色体第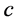 位进行交换,得到新染色体。如果该染色体不是可行解,则对他们进行可行化(同初始化)。
位进行交换,得到新染色体。如果该染色体不是可行解,则对他们进行可行化(同初始化)。
2) 变异操作
设参数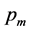 为变异概率,从
为变异概率,从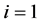 到
到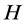 重复:产生区间
重复:产生区间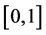 内的随机数
内的随机数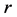 ,若
,若 ,则染色体
,则染色体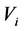 被选作父代,再对(5)式变异运算。如果该染色体不是可行解,则对他们进行可行化(同初始化),通过选择、交叉、变异,生成新一代染色体,记录最优染色体。给定进化代数
被选作父代,再对(5)式变异运算。如果该染色体不是可行解,则对他们进行可行化(同初始化),通过选择、交叉、变异,生成新一代染色体,记录最优染色体。给定进化代数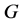 ,进行
,进行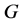 次选择、交叉和变异操作,获得最优投资比例和最优解 [11] 。
次选择、交叉和变异操作,获得最优投资比例和最优解 [11] 。
3.1.5. 信息素的初始设置
对于蚁群信息素初始化,传统方法是随机生成 [12] ,本文利用上述遗传算法得到的初始解转化为蚁群初始信息,并将信息素初始值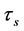 赋值为:
赋值为:
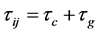 ,
,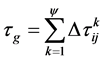 ,
,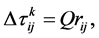 (8)
(8)
这里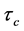 为常数,
为常数,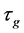 是由遗传算法得到的解转换成的信息素值,
是由遗传算法得到的解转换成的信息素值,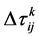 表示第
表示第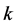 条路径中弧
条路径中弧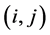 的信息素
的信息素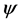 为遗传算法求得最优解的个数,
为遗传算法求得最优解的个数,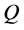 为调整系数。
为调整系数。
3.1.6. 转移概率操作
根据证券组合投资模型,定义启发函数 ,其中
,其中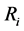 为第
为第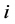 种证券的收益,
种证券的收益, 为证券组合投资的风险,
为证券组合投资的风险,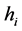 为购买
为购买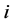 种股票的数量,则
种股票的数量,则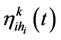 是一个反应收益和风险同时增加的指标函数,蚂蚁会倾向于选择收益和风险比值大的购买数量。
是一个反应收益和风险同时增加的指标函数,蚂蚁会倾向于选择收益和风险比值大的购买数量。
为了实现蚁群算法的群体搜索过程,设有 组人工蚂蚁,每组中有
组人工蚂蚁,每组中有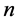 只人工蚂蚁,开始随机置于解空间
只人工蚂蚁,开始随机置于解空间 的
的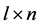 个等分区域的某些位置,给定
个等分区域的某些位置,给定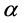 、
、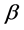 启发因子,各区域蚂蚁的状态转移概率为:
启发因子,各区域蚂蚁的状态转移概率为:
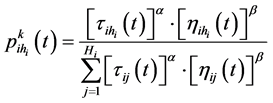 (9)
(9)
3.1.7. 信息素更新规则
为避免残留信息素过多而引起残留信息淹没启发信息,在每只蚂蚁走完一步或遍历后,对残留信息进行更新处理。具体地, 时刻在路径上的信息量按如下规则进行调整:
时刻在路径上的信息量按如下规则进行调整:
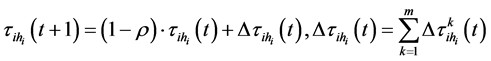 (10)
(10)
其中参数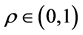 表示信息素发挥系数,
表示信息素发挥系数,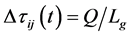 ,
, 表示信息强度,
表示信息强度,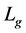 表示蚂蚁团队在本次循环中所找路径的总长度。蚂蚁团队的
表示蚂蚁团队在本次循环中所找路径的总长度。蚂蚁团队的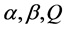 的初始值由组建团队中的个体参数构建,其构建策略按照加权平均法,权值大小根据蚂蚁所找路径的长短,具体取值如下:
的初始值由组建团队中的个体参数构建,其构建策略按照加权平均法,权值大小根据蚂蚁所找路径的长短,具体取值如下:
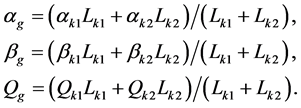 (11)
(11)
3.1.8. 遗传操作
对蚂蚁进行遗传操作,交叉算子采用一点交叉和二点交叉法。一部分蚂蚁进行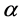 交叉,一部分蚂蚁进行
交叉,一部分蚂蚁进行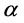 、
、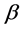 二点交叉,一部分进行
二点交叉,一部分进行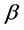 、
、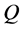 二点交叉。变异算子采用自身随机变异和种子诱导性变异,随机地对一部分蚂蚁更换
二点交叉。变异算子采用自身随机变异和种子诱导性变异,随机地对一部分蚂蚁更换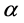 、
、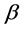 的值,找出一个种子蚂蚁,其它蚂蚁会受该蚂蚁影响而产生变异,让即将受变异的蚂蚁按照种子蚂蚁的参数比例进行变异。
的值,找出一个种子蚂蚁,其它蚂蚁会受该蚂蚁影响而产生变异,让即将受变异的蚂蚁按照种子蚂蚁的参数比例进行变异。
3.2. 遗传–蚁群算法的衔接与融合
遗传算法和蚁群算法在整体趋势上呈现图2所示的速度—时间曲线。从图2中可以看出,遗传算法在搜索的初期收敛于最优解的速度较快,但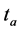 之后求最优解的效率逐渐降低。而蚁群算法在搜索初期由于缺乏信息素,搜索速度缓慢,当信息素累积到一定强度后收敛速度提高。因此本文在最佳点(
之后求最优解的效率逐渐降低。而蚁群算法在搜索初期由于缺乏信息素,搜索速度缓慢,当信息素累积到一定强度后收敛速度提高。因此本文在最佳点(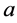 点)前采用遗传算法生成初始信息素分布,最佳点之后采取蚁群算法求取最优解 [13] 。同时为提高算法整体性能,在蚁群算法中融入遗传操作。
点)前采用遗传算法生成初始信息素分布,最佳点之后采取蚁群算法求取最优解 [13] 。同时为提高算法整体性能,在蚁群算法中融入遗传操作。
首先,在遗传算法中设置最小迭代次数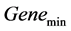 (如
(如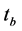 时刻)和最大迭代次数
时刻)和最大迭代次数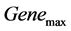 (如
(如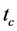 时刻)。其次,在遗传算法迭代过程中统计自带群体进化率,并设置子代群体最小进化率
时刻)。其次,在遗传算法迭代过程中统计自带群体进化率,并设置子代群体最小进化率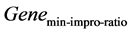 ,在设定的迭代次数内,如果连续
,在设定的迭代次数内,如果连续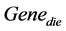 代,子代群体进化率均小于
代,子代群体进化率均小于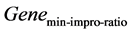 ,说明此时遗传算法优化速度已经很低,可以终止,进入蚁群算法。
,说明此时遗传算法优化速度已经很低,可以终止,进入蚁群算法。
4. 数值实验
本文以六种证券的组合为例,验证遗传–蚁群模型在优化证券组合投资中优于单一的遗传算法和蚁群算法。六种证券的收益率和风险指标(协方差)如表1所示。
预期组合证券投资收益率 ,在遗传算法中选取种群规模
,在遗传算法中选取种群规模 ,交叉概率
,交叉概率 和变异概率
和变异概率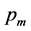 由(7)式计算,最大进化代数
由(7)式计算,最大进化代数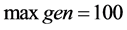 ,蚁群算法中设置信息素常数
,蚁群算法中设置信息素常数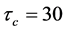 ,遗传算法转换的信息素强度值
,遗传算法转换的信息素强度值 ,蚂蚁数
,蚂蚁数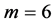 ,蚂蚁在各区域吸引强度持久性系数
,蚂蚁在各区域吸引强度持久性系数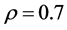 ,蚂蚁在各区域搜索中释放信息素密度
,蚂蚁在各区域搜索中释放信息素密度 ,吸引强度启发式因子
,吸引强度启发式因子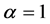 ,期望值启发因子
,期望值启发因子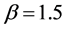 ,
,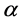 、
、 、
、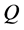 在循环 [14] 中由(11)式计算,在MATLAB环境下运行得到的最优解为:
在循环 [14] 中由(11)式计算,在MATLAB环境下运行得到的最优解为:

由此可得证券组合最小风险为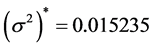 ,最大收益为
,最大收益为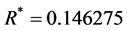 ,以及当风险偏好
,以及当风险偏好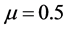 时,
时,
目标函数值 。
。
对该证券分别用简单的遗传算法(设置交叉概率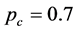 ,变异概率
,变异概率 )、蚁群算法、遗传–蚁群算法进行1000次求解,解的变化情况见下列图示。由图3可见,简单遗传算法求得目标函数最小值为
)、蚁群算法、遗传–蚁群算法进行1000次求解,解的变化情况见下列图示。由图3可见,简单遗传算法求得目标函数最小值为 ,耗时
,耗时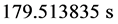 ;由图4可知,蚁群算法解得目标函数的最小值为
;由图4可知,蚁群算法解得目标函数的最小值为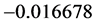 ,耗时
,耗时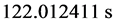 。而使用遗传–蚁群算法解得目标函数的最小值为
。而使用遗传–蚁群算法解得目标函数的最小值为 ,耗时
,耗时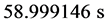 。对比三种算法的求解结果可以看出:简单遗传算法求解波动性大,蚁群算法求解波动性稳定,但是目标函数值大
。对比三种算法的求解结果可以看出:简单遗传算法求解波动性大,蚁群算法求解波动性稳定,但是目标函数值大
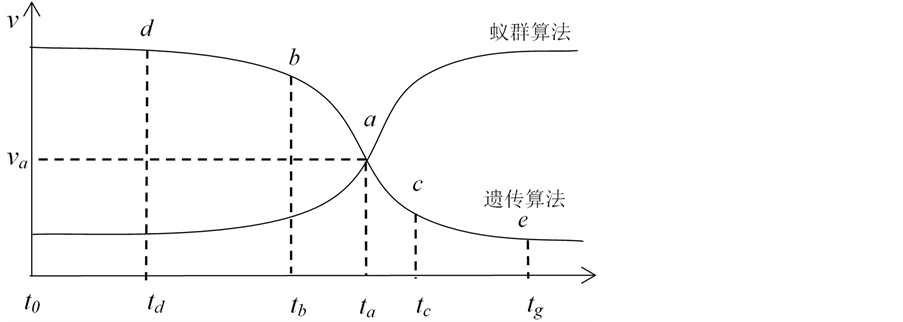
Figure 2. Velocity-time curve of genetic algorithm and ant colony algorithm
图2. 遗传算法和蚁群算法的速度–时间曲线
Table 1. The return and covariance of securities
表1. 证券的收益率和协方差
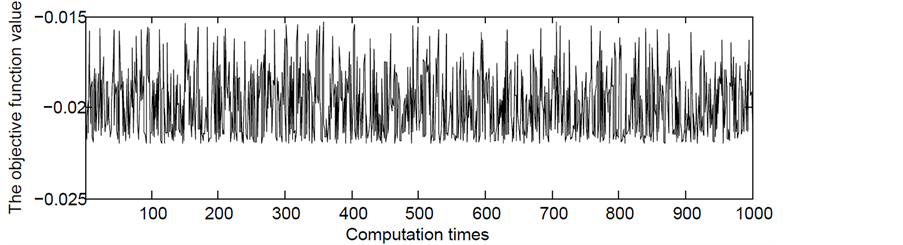
Figure 3. Simple genetic algorithm to solve the situation
图3. 简单遗传算法求解情况
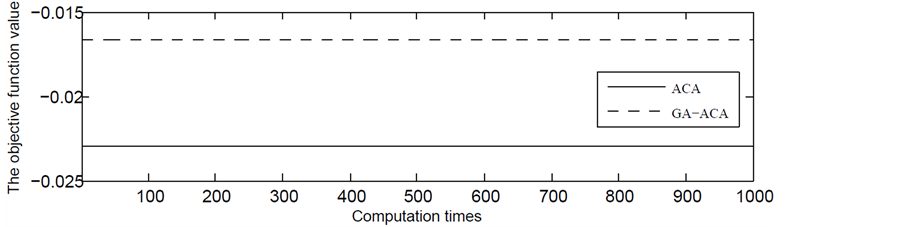
Figure 4. Comparison of ant colony algorithm and Genetic-ant colony algorithm to solve the situation
图4. 蚁群算法、遗传–蚁群算法求解情况对比图
Table 2. Statistical table for data
表2. 数据统计表
于简单遗传算法。用遗传–蚁群算法求解得到最小函数值比其他两种算法求得的目标函数值小,并且解的波动性小,时间上比简单遗传算法提高了67%,比蚁群算法提高了52%,表明利用遗传–蚁群算法获得的分配方案使得证券投资优化高于单独的遗传算法和蚁群算法。
由表2数据统计情况可得,本实验中遗传–蚁群算法获得最优解的概率为99.8%,而蚁群算法和简单遗传算法均未求得最优解,可见遗传–蚁群算法比遗传算法和蚁群算法在求解质量方面具有很大优势。
5. 结论
本文根据我国证券投资市场的现状(不允许卖空证券),提出了非负投资比例约束条件下的证券组合投资优化目标模型,给出了一新的求解该模型的遗传–蚁群算法,通过仿真分析,将该融合算法与蚁群算法、遗传算法的求解结果比较,数值实验结果表明:遗传–蚁群算法在求解质量和时间上都优于单独的蚁群算法和遗传算法。
基金项目
感谢国家自然科学基金项目(11301558),2014年度中央财经大学重大科研课题培育项目(基础理论类)的资助。
文章引用
王慧颖,衣梦涵,刘昊. 基于遗传–蚁群算法的证券组合投资优化研究
Research on Protfolio Investment Optimization Based on Genetic-Ant Colony Algorithm[J]. 建模与仿真, 2016, 05(04): 161-169. http://dx.doi.org/10.12677/MOS.2016.54021
参考文献 (References)
- 1. Markowitz, H. (1952) Portfolio Selection. The Journal of Finance, 7, 77-91. https://doi.org/10.1111/j.1540-6261.1952.tb01525.x
- 2. 刘侠, 刘红霞, 王科俊. 基于粒子群算法的证券组合投资模型的研究[J]. 投资模型的研究, 2006(16): 49-51.
- 3. 陈国良, 王熙法, 庄镇泉, 王东生. 遗传算法及其应用[M]. 北京: 北京人民邮电出版社, 1996: 56-61.
- 4. 云庆元. 遗传算法与遗传规则[M]. 北京: 冶金工业出版社, 1997: 3-7.
- 5. Dorigo, M. and Stutzle, T. (2004) Ant Colony Optimization. The MIT Press, London, England, 69-75.
- 6. 恩格尔伯里特. 计算群体智能基础[M]. 谭营, 译. 北京: 清华大学出版社, 2009: 46-51.
- 7. Dorigo, M. and Gambardella, L.M. (1997) Ant Colonies for the Travelling Salesman Problem. Biosystems, 43, 73-81. https://doi.org/10.1016/S0303-2647(97)01708-5
- 8. 肖宏峰, 谭冠政. 遗传算法在蚁群算法中的融合研究[J]. 小型微型计算机系统, 2009, 30(3): 512-517.
- 9. 李士勇. 蚁群算法及其应用[M]. 哈尔滨: 哈尔滨工业大学出版社, 2004: 78-82.
- 10. 米凯利维茨. 演化程序: 遗传算法和数据编码的结合[M]. 周家驹, 何险峰, 译. 北京: 科学出版社, 2000, 89-92.
- 11. 金海丰. 基于遗传算法的企业生产调度研究[D]: [硕士学位论文]. 武汉: 华中科技大学, 2011.
- 12. 王喆. 蚁群算法及其在火力分配问题中的应用[J]. 火力与指挥控制, 2009, 34(11): 92-94.
- 13. Ding, J.L., Chen, Z.Q. and Yuan, Z.Z. (2003) On the Combination of Genetic Algorithm and Ant Algorithm. Journal of Computer Research and Development, 40, 1351-1356.
- 14. 段海滨. 蚁群算法原理及其应用[M]. 北京: 科学出版社, 2010: 112-116.
- 15. Markowitz, H. (1952) Portfolio Selection. The Journal of Finance, 7, 77-91. https://doi.org/10.1111/j.1540-6261.1952.tb01525.x
- 16. 刘侠, 刘红霞, 王科俊. 基于粒子群算法的证券组合投资模型的研究[J]. 投资模型的研究, 2006(16): 49-51.
- 17. 陈国良, 王熙法, 庄镇泉, 王东生. 遗传算法及其应用[M]. 北京: 北京人民邮电出版社, 1996: 56-61.
- 18. 云庆元. 遗传算法与遗传规则[M]. 北京: 冶金工业出版社, 1997: 3-7.
- 19. Dorigo, M. and Stutzle, T. (2004) Ant Colony Optimization. The MIT Press, London, England, 69-75.
- 20. 恩格尔伯里特. 计算群体智能基础[M]. 谭营, 译. 北京: 清华大学出版社, 2009: 46-51.
- 21. Dorigo, M. and Gambardella, L.M. (1997) Ant Colonies for the Travelling Salesman Problem. Biosystems, 43, 73-81. https://doi.org/10.1016/S0303-2647(97)01708-5
- 22. 肖宏峰, 谭冠政. 遗传算法在蚁群算法中的融合研究[J]. 小型微型计算机系统, 2009, 30(3): 512-517.
- 23. 李士勇. 蚁群算法及其应用[M]. 哈尔滨: 哈尔滨工业大学出版社, 2004: 78-82.
- 24. 米凯利维茨. 演化程序: 遗传算法和数据编码的结合[M]. 周家驹, 何险峰, 译. 北京: 科学出版社, 2000, 89-92.
- 25. 金海丰. 基于遗传算法的企业生产调度研究[D]: [硕士学位论文]. 武汉: 华中科技大学, 2011.
- 26. 王喆. 蚁群算法及其在火力分配问题中的应用[J]. 火力与指挥控制, 2009, 34(11): 92-94.
- 27. Ding, J.L., Chen, Z.Q. and Yuan, Z.Z. (2003) On the Combination of Genetic Algorithm and Ant Algorithm. Journal of Computer Research and Development, 40, 1351-1356.
- 28. 段海滨. 蚁群算法原理及其应用[M]. 北京: 科学出版社, 2010: 112-116.
