Statistical and Application
Vol.04 No.03(2015), Article ID:16004,7
pages
10.12677/SA.2015.43019
A Sort of Multiple Life Model under Dependent Causes of Decrement
Cui Jiang1, Dabuxilatu Wang2,3*
1School of Mathematics and Information Sciences, Guangzhou University, Guangzhou Guangdong
2School of Economics and Statistics, Guangzhou University, Guangzhou Guangdong
3Lingnan Research Center for Statistical Science, Guangzhou University, Guangzhou Guangdong
*通讯作者。
Email: *wangdabu@gzhu.edu.cn
Received: Aug. 17th, 2015; accepted: Sep. 5th, 2015; published: Sep. 8th, 2015
Copyright © 2015 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
In this paper, both dependencies in decrement causes and in lives in life insurance are depicted with the copula functions, and the joint survival functions of the multiple life are compared upon the cases of independence as well as dependence. A general symmetric status of multiple life under dependent causes of decrement is considered, and some influence caused by the dependence between the individuals on the survival functions of the general symmetric status is explained.
Keywords:Decrement Causes, Multiple Life, Survival Function, Copula Function

一类相依衰减因多生命模型
蒋 翠1,王达布希拉图2,3*
1广州大学数学与信息科学学院,广东 广州
2广州大学经济与统计学院,广东 广州
3广州大学岭南统计研究中心,广东 广州
Email: *wangdabu@gzhu.edu.cn
收稿日期:2015年8月17日;录用日期:2015年9月5日;发布日期:2015年9月8日

摘 要
本文利用Copula函数刻画寿险中衰减因间以及个体之间的相依性,比较个体间独立情形与相依情形的联合生存分布。考虑相依多生命的一般对称状态在相依衰减因下的生存分布,并解释个体间相依性对一般对称状态的生存分布的影响。
关键词 :衰减因,多生命,生存分布,Copula函数

1. 引言
在一个由多个个体组成的多生命生存模型中,每个个体的生存时间往往会受到相同的经济环境或者自然环境的影响(例如地震、疾病等),而这样就使得个体间的生存时间不再是相互独立的,例如夫妻双方的寿命是正相依的[1] 。另一方面,在多元衰减模型中,各衰减因可能是完全相依的,从而导致各衰减时间完全相依,譬如:伤残与死亡之间的相依关系。因此,在生存分析中,研究各个衰减因之间的关系以及每个个体之间的关系时,经常会碰到类似上述的双重相依关系。对此,学者们多用相依竞争风险理论或多元衰减模型分别研究。
1994年,Carriere基于相依竞争风险分析提出了相依衰减理论 [2] ,在该文中,用Copula函数刻画了单生命个体受相依的多元衰减因影响的生存模型,利用粗生存分布函数与净生存分布函数的非线性微分方程组,通过粗生存分布得到了净生存分布的一个非参数估计。2007年,Kaishev等用Copula函数模拟了竞争风险生存时间的联合分布函数,分别用不同的Copula函数刻画了各风险之间的相依关系,并且在计算技术上作了很大的改进 [3] 。除了用Copula方法模拟竞争风险之间的相依性,还有许多文献试图解释个体在竞争风险下的生存时间的潜在机制 [4] [5] 。
在经典的多元衰减模型中,为了计算方便,往往假定各衰减因的衰减时间是独立的 [6] 。然而,在实际情况中,个体与个体之间以及各衰减因之间往往存在相依的情形。基于此,本文将运用Copula方法探讨相依个体与相依衰减的多生命多减因衰减模型。
2. 基本概念
对于单生命的相依多元衰减模型,Carriere [2] 和Kaishev等 [3] 在文中都有深刻的讨论。假设个体的寿命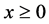 的终止受制于
的终止受制于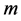 种原因中的任一个,即个体的潜在寿命是
种原因中的任一个,即个体的潜在寿命是 ,
, ,
,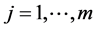 。显然,实际衰减时间是所有潜在时间
。显然,实际衰减时间是所有潜在时间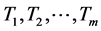 当中的最小者,即
当中的最小者,即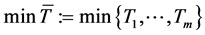 ,其可观测,但每一
,其可观测,但每一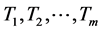 却不可观测。正如前所述,实际情形中,作用于个体的衰减因往往相依,从而考虑随机变量
却不可观测。正如前所述,实际情形中,作用于个体的衰减因往往相依,从而考虑随机变量 相依。而又如Carriere [2] 文中所提,虽然生物统计学家和精算学家常会考虑随机变量
相依。而又如Carriere [2] 文中所提,虽然生物统计学家和精算学家常会考虑随机变量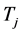 删失,但这个假设会导致一些棘手的理论问题,基于这样的事实,假设
删失,但这个假设会导致一些棘手的理论问题,基于这样的事实,假设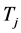 非删失,即
非删失,即 。再设
。再设 的联合分布
的联合分布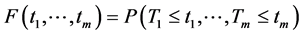 绝对连续,则对应的生存联合分布
绝对连续,则对应的生存联合分布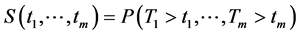 也是绝对连续。一个年龄为
也是绝对连续。一个年龄为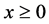 的个体的总体生存分布函数定义为
的个体的总体生存分布函数定义为

粗生存分布函数定义为
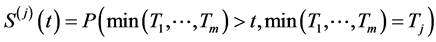
净生存分布函数定义为
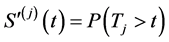
其为单独考虑衰减因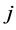 作用于
作用于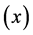 个体在
个体在 时刻之前仍未衰减的概率,用精算符号表示为
时刻之前仍未衰减的概率,用精算符号表示为 ,为了说明方便,暂用精算符号表示净生存概率,对
,为了说明方便,暂用精算符号表示净生存概率,对 有关系式
有关系式
 (1)
(1)
注意,净生存分布不可直接观测,而所能观测的是 ,因此,粗生存分布是可观测的。
,因此,粗生存分布是可观测的。
由以上定义可知,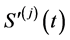 为总体生存分布函数
为总体生存分布函数 的边缘分布函数,亦称为边缘生存分布函数。
的边缘分布函数,亦称为边缘生存分布函数。
2.1. Copula函数
众所周知,联合分布函数包含了随机变量间的相依信息。而Copula函数将这种复杂的相依关系用边际变量的信息完整表现出来。
定义2.1.1 Copula是一个的函数,且满足
1)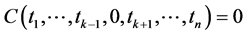 ,
,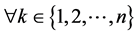 ;
;
2)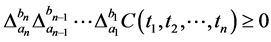 ,
,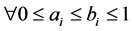 ,其中
,其中 表示的是一阶差分,即
表示的是一阶差分,即
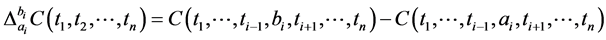
3) ,
,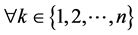 .
.
引理2.1.1 (Sklar定理(Nelsen) [6] )设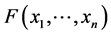 是n维向量的联合分布函数,其边缘分布函数分别为
是n维向量的联合分布函数,其边缘分布函数分别为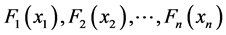 ,
,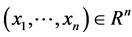 ,则必存在一个Copula函数C,使得对所有的
,则必存在一个Copula函数C,使得对所有的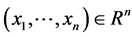 都有
都有

若边缘分布函数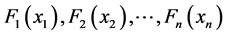 都是连续的,那么C是唯一确定的,否则C在
都是连续的,那么C是唯一确定的,否则C在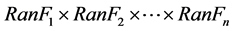 上是不唯一确定的。反之,若C是一个Copula函数,
上是不唯一确定的。反之,若C是一个Copula函数,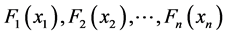 是分布函数,则由上式所定义的
是分布函数,则由上式所定义的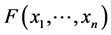 是一个联合分布函数,其边缘分布分别是
是一个联合分布函数,其边缘分布分别是 。
。
由此可知,Copula函数包含了随机变量的所有相依信息,使得处理随机变量信息更加容易,至少在确定Copula函数后可知各随机变量之间的相依结构。另一方面,对于不同类型的边缘分布函数,可以有相同的Copula函数,使得处理随机变量相依结构更加灵活。
Copula函数包括很多分布族,其中椭球分布族(例如多元的正态Copula, t-Copula等)和Archimedean分布族(例如Clayton Copula, Frank Copula等) [6] 是常见的两个分布族,本文将针对Archimedean分布族中的两类Copula函数进行讨论。
2.2. 生存Copula
对于生存Copula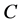 ,它是连接联合生存分布函数和边缘生存分布函数的Copula函数。与之对应的,有类似于Sklar定理的表述。因为对
,它是连接联合生存分布函数和边缘生存分布函数的Copula函数。与之对应的,有类似于Sklar定理的表述。因为对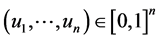 有
有
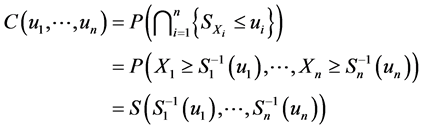
其中, ,
,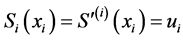 ,
, 。因此,有如下的结论:
。因此,有如下的结论:
引理2.2.1 (Carriere [2] ,Kaishev等 [3] )设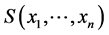 为联合生存分布函数,
为联合生存分布函数, 为其边缘分布函数且连续,则存在唯一的生存Copula
为其边缘分布函数且连续,则存在唯一的生存Copula 使得
使得
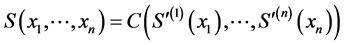 (2)
(2)
引理2.2.2 (Carriere [2] )粗生存分布函数与联合生存分布函数之间有关系式:
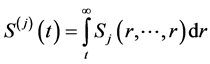 (3)
(3)
其中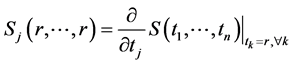 。
。
由引理2.2.1与引理2.2.2可得下列由非线性微分方程组表达的粗生存分布函数与净生存分布函数之间的关系式 [3] :
 (4)
(4)
其中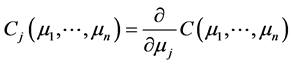 。
。
3. 一类相依衰减因下的多生命一般对称状态
本节考察相依多生命的一般对称状态在相依衰减因下的生存分布,并用生存Copula函数模拟个体间及衰减因间的相依性。
对于由 个独立个体组成的群体,可通过剩余未衰减时间
个独立个体组成的群体,可通过剩余未衰减时间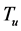 来定义状态
来定义状态 ,记
,记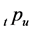 为在0时刻状态
为在0时刻状态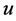 已存在,且在时刻
已存在,且在时刻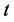 状态
状态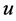 仍存在的条件概率。设
仍存在的条件概率。设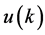 表示一般对称状态 [7] ,即至少还有
表示一般对称状态 [7] ,即至少还有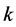 个个体没有退出,也就是第
个个体没有退出,也就是第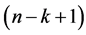 个个体退出时状态
个个体退出时状态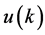 方不存在。因此,如果衰减因是死亡,那么
方不存在。因此,如果衰减因是死亡,那么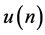 代表联合生存状态,
代表联合生存状态,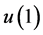 代表最后生存者状态。一般对称状态的未衰减概率
代表最后生存者状态。一般对称状态的未衰减概率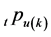 可以利用由一般概率加法公式推得的Schuette-Nesbitt公式 [7]
可以利用由一般概率加法公式推得的Schuette-Nesbitt公式 [7]
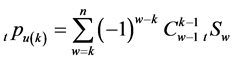 (5)
(5)
计算,其中 表示
表示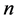 个个体中任意
个个体中任意 个个体活过
个个体活过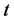 的联合概率。文献 [7] 仅考虑个体之间独立的情况,而现实中个体间可能是相依的,同时衰减因间也可能是相依的,故本文考虑
的联合概率。文献 [7] 仅考虑个体之间独立的情况,而现实中个体间可能是相依的,同时衰减因间也可能是相依的,故本文考虑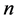 个相依个体暴露在
个相依个体暴露在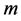 个相依衰减因的情形。为此,需计算
个相依衰减因的情形。为此,需计算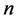 个衰减时间变量
个衰减时间变量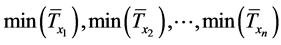 的一般对称状态的未衰减概率
的一般对称状态的未衰减概率 ,这里
,这里 。记事件
。记事件 为
为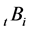 ,
,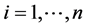 ,设
,设
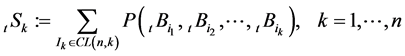
其中,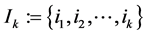 ,
, 表示由
表示由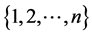 的子集
的子集 所构成的类,
所构成的类,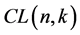 中含有
中含有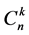 个元素,
个元素,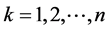 。
。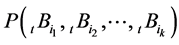 表示
表示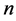 个个体中任意
个个体中任意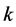 个相依个体活过t的联合概率,由Sklar定理知,存在某一生存Copula函数
个相依个体活过t的联合概率,由Sklar定理知,存在某一生存Copula函数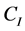 ,使得
,使得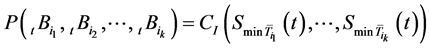 ,于是
,于是
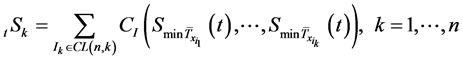
综上可得
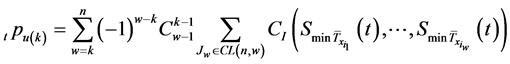 (6)
(6)
其中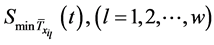 为
为 岁个体在m个相依衰减因下未衰减概率分布,
岁个体在m个相依衰减因下未衰减概率分布, 是
是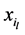 岁个体实际观测的衰减时间,从而
岁个体实际观测的衰减时间,从而 在
在 时刻的未衰减概率亦是
时刻的未衰减概率亦是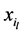 岁个体的粗生存分布在
岁个体的粗生存分布在 时刻的值。由于假定
时刻的值。由于假定 个个体的终止皆受制于
个个体的终止皆受制于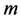 种相依衰减因,此
种相依衰减因,此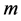 种衰减因的相依性用生存Copula函数
种衰减因的相依性用生存Copula函数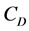 刻画,则对于
刻画,则对于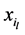 岁个体有
岁个体有
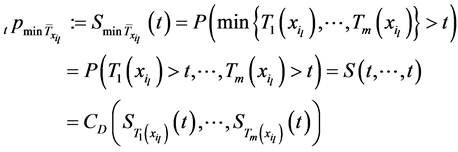
其中 为
为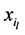 岁个体在第
岁个体在第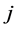 个衰减因下的净生存分布,其可通过式(4)可得。
个衰减因下的净生存分布,其可通过式(4)可得。
4. 实证分析
考虑5个相依个体在三个相依衰减因下的一般对称状态的生存分布。Frank copula (Fc), Clayton copula (GCc)以及Independence copula (Ic)函数如下:
1) Fc: ;
;
2) GCc: ;
;
3) Ic: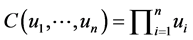 ,
,
其中,参数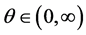 。
。
以文献 [7] 中的多元衰减表为基础,建立暴露在工作期间死亡 ,工作期间退职
,工作期间退职 ,工作期间伤残
,工作期间伤残 的30岁群体在整数年龄的粗生存分布函数值,该模型中的个体在60岁时退休,则工作期间退职以及工作期间伤残在60岁以后(包括60岁)将退出该模型,因此60岁及之后的情形就不作讨论。假设各衰减因之间的相依结构用Clayton Copula
的30岁群体在整数年龄的粗生存分布函数值,该模型中的个体在60岁时退休,则工作期间退职以及工作期间伤残在60岁以后(包括60岁)将退出该模型,因此60岁及之后的情形就不作讨论。假设各衰减因之间的相依结构用Clayton Copula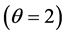 刻画,分别用过
刻画,分别用过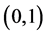 的直线拟合工作期间死亡和伤残的粗生存分布,样条函数拟合工作期间退职的粗生存分布,由式(4),利用MATLAB,得图1所示的净生存分
的直线拟合工作期间死亡和伤残的粗生存分布,样条函数拟合工作期间退职的粗生存分布,由式(4),利用MATLAB,得图1所示的净生存分
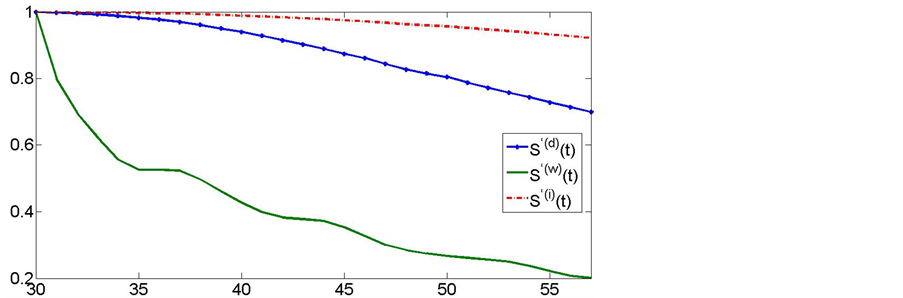
Figure 1. The net survival functions for decrement causes d, w, i under Clayton Copula
图1. Clayton Copula下的各衰减因d, w, i的净生存分布
Table 1. The values of the net survival function under the decrement causes d, w, i and for five individuals
表1. 五个个体的衰减因d, w, i净生存分布值及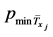
Table 2. Comparisons of probabilities under three copulas
表2. 三种Copula函数下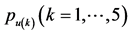 的比较
的比较
布函数。考虑该群体中分别活过32岁,35岁,40岁,45岁以及56岁的五生命群体,他们各衰减因在
未来一年未衰减的概率值由式(1)可得,其值及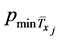 的值见表1。
的值见表1。
基于表1的结果,分别用Frank copula, Clayton copula以及Independence Copula模拟个体间的相依性,参数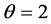 。由式(5)得表2的结果。
。由式(5)得表2的结果。
由表2可见,除了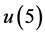 的生存分布值,其它在Fc, GCc相依假设下的生存分布值皆比独立假设的小,说明通常的个体间独立假设容易低估组合风险。同时表明若五个个体同时暴露在相同的生存环境且正相依,则只要其中一个个体衰减,其它个体暴露在风险的可能性就会增加,从而其相应状态下的生存概率就会减少。进一步,GCc相依比Fc相依的生存分布值小。对
的生存分布值,其它在Fc, GCc相依假设下的生存分布值皆比独立假设的小,说明通常的个体间独立假设容易低估组合风险。同时表明若五个个体同时暴露在相同的生存环境且正相依,则只要其中一个个体衰减,其它个体暴露在风险的可能性就会增加,从而其相应状态下的生存概率就会减少。进一步,GCc相依比Fc相依的生存分布值小。对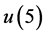 ,可见其情况与
,可见其情况与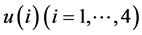 相反,因为
相反,因为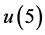 相当于五个个体的联合生存状态,只要有一个个体衰减,则五个个体都暴露在衰减风险中。在此联合生存状态下Fc, GCc相依的生存概率大于独立情形的生存概率,说明上述相依结构相对于独立结构更加稳固,加强了联合状态对衰减的抵御能力。
相当于五个个体的联合生存状态,只要有一个个体衰减,则五个个体都暴露在衰减风险中。在此联合生存状态下Fc, GCc相依的生存概率大于独立情形的生存概率,说明上述相依结构相对于独立结构更加稳固,加强了联合状态对衰减的抵御能力。
5. 结论
由以上的讨论可知,对于上述一类的多个衰减因共同作用下的多生命衰减模型,联合状态下的独立性假设高估了风险,而对于除了联合状态的一般的对称状态,其独立性假设又会低估风险,而且不同的相依结构其生命状态的分布也不同。因此,设计上述一类团体保险保单时应充分考虑个体之间的相依关系。建议在不同险种的定价中,以独立性假设为基础,然后做相应的调整。
致谢
作者衷心感谢国家自然科学基金项目(No. 11271096)的资助。
文章引用
蒋翠,王达布希拉图. 一类相依衰减因多生命模型
A Sort of Multiple Life Model under Dependent Causes of Decrement[J]. 统计学与应用, 2015, 04(03): 169-175. http://dx.doi.org/10.12677/SA.2015.43019
参考文献 (References)
- 1. Ribas, C., Marı́n-Solano, J. and Alegre, A. (2003) On the computation of the aggregate claims distribution in the indi-vidual life model with bivariate dependencies. Insurance: Mathematics and Economics, 32, 201-215. http://dx.doi.org/10.1016/S0167-6687(02)00210-X
- 2. Carriere, J.F. (1994) Dependent decrement theory. Trans. Soc. Act., 46, 45-65.
- 3. Kaishev, V.K., Dimitrova, D.S. and Haberman, S. (2007) Modelling the joint distribution of competing risks survival times using copula functions. Insurance: Mathematics and Economics, 41, 339-361. http://dx.doi.org/10.1016/j.insmatheco.2006.11.006
- 4. Gasbarra, D., Kulathinal, S.B., Dewan, I. and Nissinen, A. (2006) Testing dependence between the failure time and failure modes: An application of enlarged filtration. Journal of Statistical Planning and Inference, 136, 1669-1686. http://dx.doi.org/10.1016/j.jspi.2005.07.002
- 5. Tiwari, R., Kulasekera, K.B. and Park, C. (2006) Nonparametric tests for cause specific hazard rates with censored data for competing risks among several groups. Journal of Statistical Planning and Inference, 136, 1718-1745. http://dx.doi.org/10.1016/j.jspi.2004.12.016
- 6. Nelsen, R.B. (2006) An introduction to copulas. 2nd Edition, Springer-Verlag, New York.
- 7. Gerber, H.U. (1997) Life insurance mathematics. Spring-Verlag.
