Statistics and Application
Vol.06 No.01(2017), Article ID:19904,8
pages
10.12677/SA.2017.61007
Analysis of Energy Consumption Influencing Factors in China Based on the Lasso Method
Xiaotong Li, Danyan Qin, Minghui Lv
Science College, China University of Petroleum, Beijing

Received: Feb. 25th, 2017; accepted: Mar. 14th, 2017; published: Mar. 17th, 2017

ABSTRACT
With the acceleration of economic development and the increasing demand for resources, energy consumption shows a rising trend in recent years. To ensure the stable, sustainable and healthy development of China’s economy, it is necessary to study on consumption factors and to forecast energy consumption demand reasonably. As so far, scholars have used simple linear regression, principal component regression and ridge regression method for analyzing China’s energy consumption factors, but models achieved from these studies may be too lean to find more comprehensive energy consumption factors. While according to the related data of domestic energy consumption during 2000-2012, this paper chooses a new method—Lasso method to make regression model for domestic energy consumption, and then we get the main energy consumption effecting factors: economic development, demographic factor, industrial structure, technological progress, energy consumption efficiency and energy price factor, so we can control energy consumption through these main factors. Additionally, we use stepwise regression and ridge regression to make regression models, the results got from the Lasso, stepwise regression and ridge regression are compared, the study shows the Lasso method is better than the other methods in terms of variable selection, because it could find more comprehensive energy consumption factors; for predictions of 2013 and 2014, Lasso method is more accurate than the other two methods.
Keywords:Energy Consumption, Lasso, Stepwise Regression, Ridge Regression
基于Lasso方法的我国能源消费影响因素分析
李晓童,覃丹艳,吕明慧
中国石油大学(北京)理学院,北京
收稿日期:2017年2月25日;录用日期:2017年3月14日;发布日期:2017年3月17日

摘 要
随着经济发展的加快和资源需求量的加大,能源消费呈现出连年攀升的态势,能源消费影响因素的研究及能源消费需求的合理预测,对保证我国经济平稳持续健康发展是十分必要的。目前学者们分别用过简单线性回归法、主成分回归法及岭回归法对我国能源消费影响因素进行分析,但这些研究得到的模型可能太过精简而未能较为全面地找出能源消费的主要影响因素。而本文依据2000年~2012年我国能源消费总量的相关数据,针对变量偏多,观测数据少的特点选用了Lasso方法对我国能源消费影响因素建立了回归模型,得到了影响我国能源消费的主要因素有经济增长因素、人口增长因素、产业结构因素、技术进步因素、能源利用效率因素以及能源价格因素,因此,我们可主要从这些因素入手,对能源消费加以管理和控制。同时我们还用逐步回归法和岭回归法分别建立了回归模型,并将Lasso方法得到的结果与其进行比较,结果表明Lasso方法在能源消费影响因素的选择方面,比其他两种方法更为全面地找出能源消费的主要影响因素,在对2013年及2014年能源消费总量预测方面,Lasso方法比其他两种方法更为精确。
关键词 :能源消费,Lasso方法,逐步回归法,岭回归法

Copyright © 2017 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
能源是一国经济发展的驱动力和重要的物质保障。高速发展的经济使我国能源消费现状体现出消费量增长迅速、消费结构以煤为主、能源进口依存度日趋严峻等特征。按照中国经济发展目标,要实现2020年GDP总量在2000年的基础上翻两番达到全面建成小康社会的目标,能源供应至关重要。我国的能源有限,因此通过对我国能源消费影响因素的研究以及对能源消费需求的合理预测,为合理制定能源战略及保证我国经济平稳持续健康发展是十分有必要的。对能源消费影响因素的研究成果已有很多。佟阿思根等(2008) [1] 从能源消费、能源消费结构、能源进口依存度三方面阐述了我国能源消费现状,并用简单线性回归的方法对能源需求进行了预测;赵建辉(2014) [2] 用主成分回归的方法对我国能源消费影响因素进行了研究,结果表明经济发展、能源价格和产业结构是影响能源消费的主要因素,并对比了回归方程的预测值与真实值的差距;张丹平(2012) [3] 用岭回归的方法对我国能源消费影响因素进行了研究,用岭迹图的方法剔除变量及确定岭参数 ,最后得到了影响我国能源消费因素有产业结构因素、人口因素以及固定资产投资因素;Geem和Roper (2009) [4] 、Ekonomou (2010) [5] 、Oludolapo等(2012) [6] 选了经济增长因素、人口因素、能源进口量及能源出口量作为自变量用人工神经网络技术来分别估算韩国、希腊和南非的能量消费量。这些研究成果中有的在最初进行分析时所选的影响因素本来就很少,有的是经过变量压缩或剔除之后留下的影响因素太少,模型太过于精简而不利于对能源消费影响因素这一问题的进行分析。而且,影响能源消费的因素有很多,我们不能简单地从两三个因素去分析,我们最终希望得到的模型既简洁但又不丢失太多对能源消费有影响的因素,即希望能够较为全面准确地找到能源消费的主要影响因素,并给出较高精度的预测值。
,最后得到了影响我国能源消费因素有产业结构因素、人口因素以及固定资产投资因素;Geem和Roper (2009) [4] 、Ekonomou (2010) [5] 、Oludolapo等(2012) [6] 选了经济增长因素、人口因素、能源进口量及能源出口量作为自变量用人工神经网络技术来分别估算韩国、希腊和南非的能量消费量。这些研究成果中有的在最初进行分析时所选的影响因素本来就很少,有的是经过变量压缩或剔除之后留下的影响因素太少,模型太过于精简而不利于对能源消费影响因素这一问题的进行分析。而且,影响能源消费的因素有很多,我们不能简单地从两三个因素去分析,我们最终希望得到的模型既简洁但又不丢失太多对能源消费有影响的因素,即希望能够较为全面准确地找到能源消费的主要影响因素,并给出较高精度的预测值。
Lasso回归提出至今,已被广泛应用在生物医学、金融分析、图像处理、机器学习等众多领域,它在变量选择与参数压缩估计方面表现比较好。Lasso回归根据与被解释变量相关性的大小来选择回归方程中的解释变量,能使最终模型既简洁又不丢失与被解释变量密切相关的解释变量,且有较高的预测精度。本文用Lasso方法对我国能源消费的影响因素进行分析,首先我们根据问题的实际背景以及获取数据的局限性初步给出了七个影响我国能源消费的因素,分别为:经济增长因素、人口增长因素、产业结构因素、技术进步因素、投资因素、能源利用效率因素以及能源价格因素。基于2000年~2012年我国能源消费总量的相关数据,我们选用了Lasso方法对我国能源消费影响因素建立了回归模型,得到了影响我国能源消费的主要因素以及给出了2013、2014年能源消费总量的预测值。同时我们还利用逐步回归和岭回归对能源消费影响因素这一问题分别建立回归模型,并将Lasso方法得到的结果与其在变量选择、预测精度方面进行了比较,在变量选择即能源消费影响因素的选择方面,Lasso方法比其他两种方法更为全面地找出能源消费的主要影响因素,在能源消费总量的预测方面,Lasso方法比其他两种方法更为精确。
2. Lasso方法的介绍
Robert Tibshirani于1996提出了一种新的变量选择技术Lasso [7] ,即Least Absolute Shrinkage and Selection Operator。此方法用模型系数的绝对值函数作为惩罚来压缩模型系数,使一些回归系数缩小,甚至使一些绝对值较小的系数直接变为0。
设有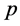 个自变量
个自变量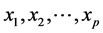 和因变量
和因变量 ,它们之间可建立如下的线性回归模型:
,它们之间可建立如下的线性回归模型:
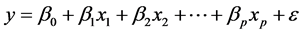 (1)
(1)
其中 为常数项,
为常数项,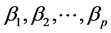 为回归系数,
为回归系数,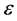 是随机扰动项。
是随机扰动项。
设有数据 ,其中
,其中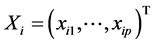 为自变量,
为自变量,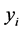 为因变量。同时假设
为因变量。同时假设 为标准化数据,即
为标准化数据,即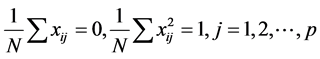 ,令
,令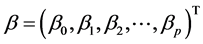 ,则模型(1)中未知参数
,则模型(1)中未知参数 的普通最小二乘估计为:
的普通最小二乘估计为:
 (2)
(2)
其中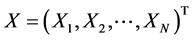 为回归方程的系数矩阵。
为回归方程的系数矩阵。
模型(1)中未知参数 的Lasso估计可定义为:
的Lasso估计可定义为:
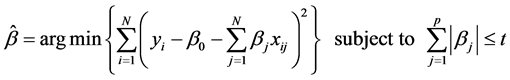 (3)
(3)
其中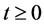 为调和参数。
为调和参数。
调和参数 在估计时用来控制回归系数
在估计时用来控制回归系数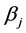 的压缩量,记
的压缩量,记 ,则当
,则当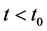 时可使一些回归系数
时可使一些回归系数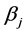
缩小并趋向于0,甚至使一些回归系数 的估计值就等于0。每一个
的估计值就等于0。每一个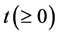 值都会通过(3)式对应于一个Lasso估计值
值都会通过(3)式对应于一个Lasso估计值 ,经过若干步后可得不同
,经过若干步后可得不同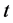 值下的所有Lasso估计值。这时,我们可用交叉验证法、广义交叉验证法、
值下的所有Lasso估计值。这时,我们可用交叉验证法、广义交叉验证法、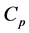 准则、赤池信息量准则(AIC)、贝叶斯信息准则(BIC)确定一个最优调和参数
准则、赤池信息量准则(AIC)、贝叶斯信息准则(BIC)确定一个最优调和参数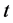 ,从而选出最佳模型。
,从而选出最佳模型。
Lasso问题的求解实质是解一个带不等式约束的二次规划问题,Bradley Efron (2004) [8] 等提出的最小角回归(Least Angle Regression)算法,和著名的向前选择法(Forward Selection)一样,一开始令所有的系数为零,先找出和因变量相关性最强的自变量,记为 ,然后我们沿着
,然后我们沿着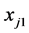 的方向上找出另一个自变量,记为
的方向上找出另一个自变量,记为 ,使得它与当前的残差有同样的相关性。接下来不同于向前选择法继续沿着
,使得它与当前的残差有同样的相关性。接下来不同于向前选择法继续沿着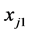 的方向,最小角回归算法沿着平分前两个变量夹角的方向,找到变量
的方向,最小角回归算法沿着平分前两个变量夹角的方向,找到变量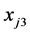 ,使得它满足相关性最强,然后在沿着平分前三个变量夹角的方向找第四个变量,以此类推,直到找到所有变量,算法终止。对最小角回归算法的一个修正即要求进行每一步计算时要求当前得到的
,使得它满足相关性最强,然后在沿着平分前三个变量夹角的方向找第四个变量,以此类推,直到找到所有变量,算法终止。对最小角回归算法的一个修正即要求进行每一步计算时要求当前得到的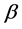 估计值必须与相关系数符号一致,这就能得到了Lasso算法,从而也就解决Lasso方法的计算问题。
估计值必须与相关系数符号一致,这就能得到了Lasso算法,从而也就解决Lasso方法的计算问题。
3. 我国能源消费影响因素的实证分析
3.1. 我国能源消费影响因素指标的选取以及数据来源
我们根据问题的实际背景以及获取数据的局限性初步给出了七个影响我国能源消费的因素,分别为:经济增长因素、人口增长因素、产业结构因素、技术进步因素、投资因素、能源利用效率因素以及能源价格因素。为方便对能源消费影响因素进行实证分析,需要对以上各个影响因素进行量化,即选择一些能反映上述影响因素的指标,如表1所示。
根据《中国统计年鉴》及《中国能源统计年鉴》,得到我国2000~2012年能源消费总量和对影响因素量化后的部分数据如表2所示。
3.2. 基于Lasso方法的模型的建立
本文中设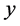 为能源消费总量,影响
为能源消费总量,影响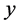 的七个自变量分别是:
的七个自变量分别是: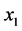 (经济增长因素)、
(经济增长因素)、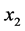 (人口增长因素)、
(人口增长因素)、 (产业结构因素)、
(产业结构因素)、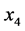 (投资因素)、
(投资因素)、 (技术进步因素)、
(技术进步因素)、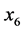 (能源利用效率因素)、
(能源利用效率因素)、 (能源价格因素)。我们考虑建立线性回归模型
(能源价格因素)。我们考虑建立线性回归模型
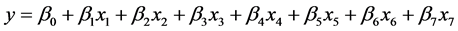
其中,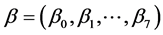 是未知参数。
是未知参数。
由于自变量相对较多且它们之间可能存在着多重共线性时,通常用普通最小二乘法建立回归模型效果较差,因此,首先我们采用方差扩大因子法进行多重共线性的检验。方差扩大因子定义为
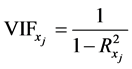
其中,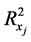 为
为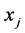 对其余自变量的复决定系数。当
对其余自变量的复决定系数。当 时,说明
时,说明 与其余自变量之间有严重多重共线性。利用SAS软件 [9] 的proc reg过程建立最小二乘回归模型的同时,我们得到了每个自变量的方差扩大因子
与其余自变量之间有严重多重共线性。利用SAS软件 [9] 的proc reg过程建立最小二乘回归模型的同时,我们得到了每个自变量的方差扩大因子 ,输出结果如图1所示。从图1看到,
,输出结果如图1所示。从图1看到, ,
,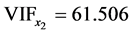 ,
,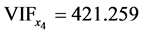 ,
,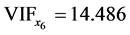 ,即变量
,即变量 的方差扩大因子都超过了10,说明这四个影响因素与其他因素之间存在着严重的共线性。
的方差扩大因子都超过了10,说明这四个影响因素与其他因素之间存在着严重的共线性。
在处理变量相对较多且出现多重共线性时,Lasso方法是一种有效的处理方法。因此,我们运用Lasso方法对选取的七个影响能源消费的因素进行回归分析,利用SAS软件的proc glmselect 过程,选择Lasso方法,只需要9步,就找到了Lasso方法全部的解。Lasso解的回归路径如图2所示,Lasso回归的变量选择路径以及各种准则统计量的值如表3所示。
从表3我们可以看到,不同的准则可能得到的模型会不一样,我们既希望得到的模型各项衡量准则较优,又要考虑实际问题的需要,在综合考虑后选择第8步得到的Lasso解为最优解,即得到最佳模型,因为在第8步时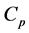 统计量和赤池信息量AIC都达到最小,自由度调整复决定系数达最大,且得到的能源消费影响因素较为全面,能够给出合理的经济解释,则标准化回归方程为:
统计量和赤池信息量AIC都达到最小,自由度调整复决定系数达最大,且得到的能源消费影响因素较为全面,能够给出合理的经济解释,则标准化回归方程为:
Table 1. Index selection
表1. 指标选取
Table 2. 2000~2012 Annual data
表2. 2000~2012年年度数据
Table 3. The value of the Lasso variable selection path and the value of various criteria statistics
表3. Lasso回归的变量选择路径与各种准则统计量的值

Figure 1. Multicollinearity diagnosis
图1. 多重共线性诊断
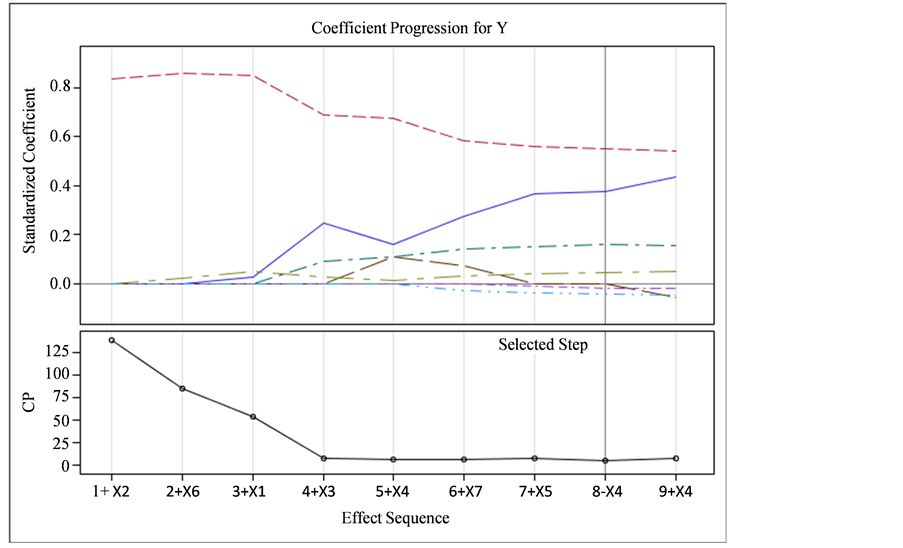
Figure 2. Lasso Regression path graph
图2. Lasso解的回归路径图

还原后的回归方程为:

运用Lasso方法得到的影响能源消费的主要因素有经济增长因素( )、人口增长因素(
)、人口增长因素( )、产业结构因素(
)、产业结构因素(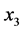 )、技术进步因素(
)、技术进步因素(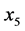 ) 、能源利用效率因素(
) 、能源利用效率因素(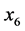 )以及能源价格因素(
)以及能源价格因素( )。由回归方程看出,1) 我国能源消费受经济增长、人口增长、产业结构这三个因素的影响比较大,参数估计分别为0.377,0.548,0.159。人口增长因素是影响能源消费最大的因素,人口总数越多,能源消耗越多。能源消费与经济增长呈正相关,国内生产总值每增加一个单位,会使能源消费增加0.377个单位。三大产业对能源消费的需求大不相同,第二产业包括我国工业、制造业和建筑业等高耗能产业,因此第二产业在GDP中占得比重越大,消耗的能源也就越多。2) 能源消费受技术进步、能源利用效率、能源价格的影响比较小,参数估计分别为−0.018,0.044,−0.042。技术进步可以大幅度提高能源的利用效率,同时会推进新能源的开发与利用,从而会减少传统能源的利用。一般而言,能源利用效率的增高有助于能源消费量的减少,但它与能源消费呈现的正负相关性取决于各自增长的速度。当能源利用效率的增长速度不足以弥补能源消费的增速时,两者就呈现正相关。能源消费与能源价格成反比,能源价格每增加1个单位,能源消费量减少0.042个单位。运用Lasso方法得到的模型与实际情况相吻合。
)。由回归方程看出,1) 我国能源消费受经济增长、人口增长、产业结构这三个因素的影响比较大,参数估计分别为0.377,0.548,0.159。人口增长因素是影响能源消费最大的因素,人口总数越多,能源消耗越多。能源消费与经济增长呈正相关,国内生产总值每增加一个单位,会使能源消费增加0.377个单位。三大产业对能源消费的需求大不相同,第二产业包括我国工业、制造业和建筑业等高耗能产业,因此第二产业在GDP中占得比重越大,消耗的能源也就越多。2) 能源消费受技术进步、能源利用效率、能源价格的影响比较小,参数估计分别为−0.018,0.044,−0.042。技术进步可以大幅度提高能源的利用效率,同时会推进新能源的开发与利用,从而会减少传统能源的利用。一般而言,能源利用效率的增高有助于能源消费量的减少,但它与能源消费呈现的正负相关性取决于各自增长的速度。当能源利用效率的增长速度不足以弥补能源消费的增速时,两者就呈现正相关。能源消费与能源价格成反比,能源价格每增加1个单位,能源消费量减少0.042个单位。运用Lasso方法得到的模型与实际情况相吻合。
3.3. 三种回归分析结果的比较
我们利用逐步回归和岭回归针对能源消费这一问题也分别建立了回归模型,并将Lasso方法得到的结果与其进行了比较,结果如表4所示。
Table 4. Standardized parameter estimation
表4. 标准化参数估计
从表4结果可以看出,三种方法得到的回归模型中都包含人口增长因素和产业结构因素,其参数估计的符号相同,数值较为接近,而且三个回归模型中人口增长因素的回归系数最大,说明我国能源消费受人口增长因素的影响最大。但是,逐步回归每一步迈得过长,对变量的删减度过大,最终只保留三个变量,导致经济增长这一主要影响能源消费的因素也被剔除,模型太过精简,在该案例中不建议使用;岭回归通过观察岭迹图根据经验人为剔除变量最终保留四个变量,选择变量的主观性太强导致模型解释性不好,而Lasso方法不会像逐步回归那样出现变量删减过度的问题,它在回归方程中尽可能地留下与能源消费密切相关的变量,给出的参数估计符合实际意义,比较全面地分析了影响我国能源消费的因素,而且,Lasso方法用模型系数的绝对值函数作为惩罚来压缩模型系数,使一些绝对值较小的系数直接变为0,在选择变量即能源消费影响因素方面就避免了岭回归的主观性,使得到的模型更加直观。
最后,由于2013年和2014年的数据中,能源利用效率因素这一变量的数据是缺失的,我们先利用缺失数据的填补方法对其进行填补,再根据上述三种方法得到的回归模型,分别给出2013年及2014年的能源消费总量的预测值,并与观测到的真实值进行了比较,结果如表5所示。
从表5的对比结果可以看到,用Lasso方法得到的能源消费总量预测值的相对误差为0.11、0.48,比岭回归、逐步回归方法得到的预测值更精确。
4. 结论
本文依据2000年~2012年我国能源消费相关数据,运用了Lasso方法对能源消费影响因素问题进行分析,最终得出了影响我国能源消费的主要因素有经济增长因素、人口增长因素、产业结构因素、能源利用效率因素以及能源价格因素。标准化回归方程表明:我国能源消费受经济增长、人口增长、产业结构这三个因素的影响比较大,参数估计分别为0.377,0.548,0.159;受技术进步、能源利用效率、能源价格的影响比较小,参数估计分别为−0.018,0.044,−0.042。因此在对能源消费进行管理和控制时,一方面我们可以主要从影响大的因素着手,在不影响经济增长以及我国人口庞大这一事实短期内无法改变的条件下要提高人口素质及居民的环保节约意识、优化产业结构;另一方面不忽视影响小的因素,促使新技术的发展从而大幅度提高能源利用效率,兼顾能源定价机制,加速能源价格市场化。
其次,我们用逐步回归和岭回归对我国能源消费影响因素这一问题分别建立回归模型,并将Lasso方法进行得到的结果与其在能源消费影响因素的选择和预测精度方面进行了比较。在能源消费影响因素的选择方面,三种方法得到的回归模型中都包含人口增长因素和产业结构因素,其参数估计的符号相同,而且都得到我国能源消费受人口增长因素的影响最大。但是,逐步回归由于对变量的删减度过大而导致经济增长这一主要影响能源消费的因素被剔除,它仅留下三个变量模型过于精简,岭回归选择变量的主
Table 5. Comparison of the results of Lasso regression, ridge regression and stepwise regression
表5. Lasso回归、岭回归、逐步回归预测结果的比较
观性太强导致模型解释性不好,而Lasso方法既不会像逐步回归那样出现变量删减过度的问题,也可以避免了像岭回归那样选择变量太过主观,它尽可能地留下与能源消费密切有关的变量,给出的参数估计符合实际意义,比较全面地分析了影响我国能源消费的因素。在预测精度方面,我们用这三种方法得到的回归模型对2013年及2014年的能源消费总量做了预测,并与真实值进行比较,结果表明Lasso方法的预测精度比其他两种方法都要高。所以在今后处理自变量相对较多观测数据较少的问题时,不妨考虑采用Lasso方法,可能得到的效果要优于比其他方法。
基金项目
中国石油大学(北京)本科教学质量与教学改革工程重点项目,项目编号21G15043。
文章引用
李晓童,覃丹艳,吕明慧. 基于Lasso方法的我国能源消费影响因素分析
Analysis of Energy Consumption Influencing Factors in China Based on the Lasso Method[J]. 统计学与应用, 2017, 06(01): 73-80. http://dx.doi.org/10.12677/SA.2017.61007
参考文献 (References)
- 1. 佟阿思根, 侯俊芝. 中国能源消费现状及能源需求预测[J]. 内蒙古民族大学学报, 2008(3): 83-85.
- 2. 赵建辉. 基于主成分回归模型的我国能源消费影响因素分析[J]. 中国矿业, 2014(1): 44-49.
- 3. 张丹平. 基于岭回归方法的我国能源消费影响因素研究[J]. 统计与决策, 2012(21): 146-148.
- 4. Geem, Z.W. and Roper, W.E. (2009) Energy Demand Estimation of South Korea Using Artificial Neural Network. Energy Policy, 37, 4049-4054. https://doi.org/10.1016/j.enpol.2009.04.049
- 5. Ekonomou, L. (2010) Greek Long-Term Energy Consumption Prediction Using Artificial Neural Networks. Energy, 35, 512-517. https://doi.org/10.1016/j.energy.2009.10.018
- 6. Oludolapo, O.A., Jimoh, A.A. and Kholopane, P.A. (2012) Comparing Performance of MLP and RBF Neural Network Models for Predicting South Africa’s Energy Consumption. Journal of Energy in Southern Africa, 23, 40-46.
- 7. Tibshirani, R. (1996) Regression Shrinkage and Selection via the Lasso. Journal of the Royal Statistical Society. Series B (Methodological), 58, 267-288.
- 8. Efron, B., Hastie, T., Johnstone, I., et al. (2004) Least Angle Regression. The Annals of Statistics, 32, 407-499. https://doi.org/10.1214/009053604000000067
- 9. 高惠璇, 耿直, 李贵斌, 等. SAS系统SAS/STAT软件使用手册[M]. 北京: 中国统计出版社, 1997.
