Advances in Applied Mathematics
Vol.3 No.02(2014), Article
ID:13569,6
pages
DOI:10.12677/AAM.2014.32014
A Numerical Method for Solving the Nonlinear Algebraic Equations
Yangtze College, East China Institute of Technology, Fuzhou
Email: 2318284432@qq.com
Copyright © 2014 by author and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received: Mar. 22nd, 2014; revised: Apr. 18th, 2014; accepted: Apr. 26th, 2014
ABSTRACT
In this paper, we will use a new method of elimination and the dichotomy of the nonlinear equation to common research the numerical solution of equations.
Keywords:A New Method of Elimination, Dichotomy

非线性代数方程组的一种数值解法
周亚南
东华理工大学长江学院,抚州
Email: 2318284432@qq.com
收稿日期:2014年3月22日;修回日期:2014年4月18日;录用日期:2014年4月26日

摘 要
本文将用一种新的消元法和非线性方程的二分法来共同研究方程组的数值解。
关键词
新消元法,二分法

1. 引言
非线性代数方程组的求解问题是一个古老的问题,在社会飞速发展的今天,它被应用到许多地方,比如说计算机辅助设计图形,以及来自工程、机械等的几何约束问题,最终都将产生一个大型的非线性代数方程组,其中常见的求解非线性代数方程组的方法有非线性的Jacobi迭代法、Gauss-Seidel迭代法、SOR迭代法、牛顿迭代法及改进的牛顿迭代法等[1] 。2014年初周亚南首先提出了一种引入多参变量的一种消元法[2] ,在了解了这种消元法后,将其应用到非线性代数方程组的数值解法中,通常非线性代数方程组表示为:
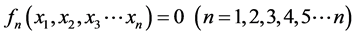 (1)
(1)
为了能很好的介绍清楚这种消元法,对于(1)式引进一些吴标记法[3] :多项式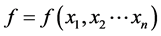 变元
变元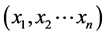 中下标最大下标称为多项式
中下标最大下标称为多项式 的主变元,记为
的主变元,记为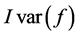 ;多项式
;多项式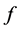 的主变元
的主变元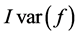 的下标定义为多项式的类,记为
的下标定义为多项式的类,记为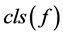 ;多项式关于变元
;多项式关于变元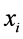 的次数记为
的次数记为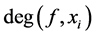 ,主变元的次数记为
,主变元的次数记为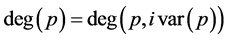 ;多项式的长度定义为多项式的项数,记为
;多项式的长度定义为多项式的项数,记为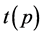 。下面引入新的标记:多项式
。下面引入新的标记:多项式 中的各项记为
中的各项记为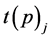 ;单项式
;单项式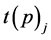 中元素的个数记为
中元素的个数记为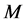 ,每个元素的幂记为
,每个元素的幂记为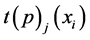 ;单项式
;单项式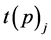 中所有元素的幂之和记为
中所有元素的幂之和记为 。
。
2. 消元法
上面已经提到引入多参变量的一种消元法,为此引入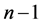 个参变量,记为
个参变量,记为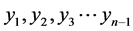 ,并且使其满足下面的式子关系
,并且使其满足下面的式子关系
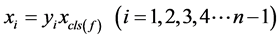 (2)
(2)
后将(2)式代入到(1)中,将得到一个新的代数方程组,记为
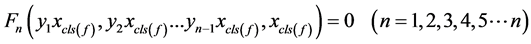 (3)
(3)
将式(3)重新分配成为下面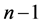 个方程组
个方程组
 (4)
(4)
对这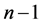 个方程组进行消元,可以得到
个方程组进行消元,可以得到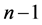 个方程式,记为
个方程式,记为
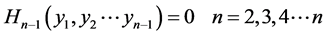 (5)
(5)
同时联立这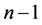 个方程式,将得到一个新的方程组,用同样的方式标记为(5),例:方程组
个方程式,将得到一个新的方程组,用同样的方式标记为(5),例:方程组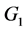 的消元,这里主要是消去未知量
的消元,这里主要是消去未知量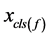 (
( 同样也是消去未知量
同样也是消去未知量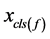 ),为此讨论下面方程组的消元法(即
),为此讨论下面方程组的消元法(即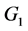 变形后的方程组)
变形后的方程组)
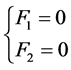 (6)
(6)
为了讨论好这种消元法,还需进行这样的标记,将多项式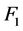 分为两类,一类是含有未知量
分为两类,一类是含有未知量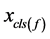 ,记为
,记为 ,一类是不含未知量
,一类是不含未知量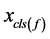 ,记为
,记为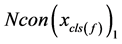 ,由式子(6)中的
,由式子(6)中的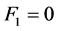 可以得到下面的方程式
可以得到下面的方程式
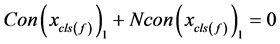 (7)
(7)
同理由式子(6)中的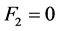 可以得到下面的方程式
可以得到下面的方程式
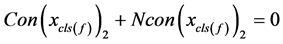 (8)
(8)
由(7) (8)可以得到下面的方程组
 (9)
(9)
由方程组(9)可以得到下面的多项式
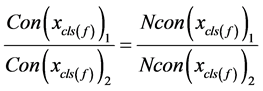 (10)
(10)
现在来分析(10),其中 、
、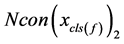 式必然不会为零,且(10)式中必然会至少消去一个
式必然不会为零,且(10)式中必然会至少消去一个 ,将(10)变形得到下面的式子
,将(10)变形得到下面的式子
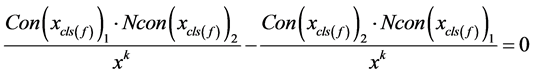 (k为可约次数) (11)
(k为可约次数) (11)
这样就起到了消元的目的,之后将方程式(11)和(7)或(8)中的一个联立方程组{这里只能和(7)(8)中的一个联立方程组,且在以后的子联立中以第一次联立的方程式为主},这样在每次联立后起到一次消元的目的,这一次一次的联立我们称之为子联立,在一次次的消元过程后,我们必定会得到下面一个方程式
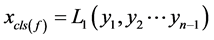 (12)
(12)
将(12)式代入第一次未联立的那个方程式中,就消掉了未知量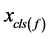 ,得到了所需要的方程式
,得到了所需要的方程式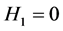 ,同理可以得到
,同理可以得到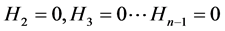 ,联立(这里的联立不是子联立)就得到了所需要的方程组(5),再对(5)进行上述循环,可以得到一个含有
,联立(这里的联立不是子联立)就得到了所需要的方程组(5),再对(5)进行上述循环,可以得到一个含有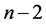 个未知量的方程组,依次循环最后可以得到到一个方程式,这样就完成了消元。
个未知量的方程组,依次循环最后可以得到到一个方程式,这样就完成了消元。
3. 数值解法的实现
3.1. 消元法在非线性代数方程组的数值解法上的应用
定义3.11:定义原方程组为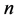 级方程组,第一次消元后得到的方程组为
级方程组,第一次消元后得到的方程组为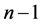 级方程组,即方程组的级数等于原方程组的级数减去消元的次数,最后的方程式定义为一级方程式。从上面的消元过程的介绍,不难会想到去求解这个一级方程式的数值解,然后代入到二级方程组去求解二级方程组的解(这里会有增解,要舍去),然后再代入三级方程组(同样有增解),依次这样做下去,直到得到原方程组的解(即
级方程组,即方程组的级数等于原方程组的级数减去消元的次数,最后的方程式定义为一级方程式。从上面的消元过程的介绍,不难会想到去求解这个一级方程式的数值解,然后代入到二级方程组去求解二级方程组的解(这里会有增解,要舍去),然后再代入三级方程组(同样有增解),依次这样做下去,直到得到原方程组的解(即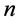 级方程组的解),而进行这个过程,不难发现,它都可以转换为求解方程式的数值解,所以可以用二分法、不动点迭代法、Newton迭代法或者割线法等方法去依次求解方程式的数值解,最后求得原方程组的数值解(在下文主要以二分法来求解方程组数值解),例如上面的方程组(5),假定已经求得其方程组的解
级方程组的解),而进行这个过程,不难发现,它都可以转换为求解方程式的数值解,所以可以用二分法、不动点迭代法、Newton迭代法或者割线法等方法去依次求解方程式的数值解,最后求得原方程组的数值解(在下文主要以二分法来求解方程组数值解),例如上面的方程组(5),假定已经求得其方程组的解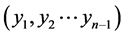 ,那么仅需将
,那么仅需将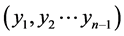 代入方程组(3)中的一个式子中求得未知量
代入方程组(3)中的一个式子中求得未知量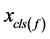 的数值解,然后用(3)中的其余方程式检验其解的正确性即可,最后得到了
的数值解,然后用(3)中的其余方程式检验其解的正确性即可,最后得到了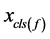 的数值解,仅需代入式子(2),就可以得到一组关于原方程组的解。总结:同样对于
的数值解,仅需代入式子(2),就可以得到一组关于原方程组的解。总结:同样对于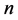 级方程组的每一级方程组,可以同样采用二分法去求每一级方程组的数直解,但这种方法必须从一级方程式开始,再依次求二级…直到得到原方程组的数值解。
级方程组的每一级方程组,可以同样采用二分法去求每一级方程组的数直解,但这种方法必须从一级方程式开始,再依次求二级…直到得到原方程组的数值解。
3.2. 解法的收敛速度
在上面主要用二分法求解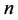 级方程组的数值解,且需要求出每一级方程组的数值解,所以每一级方程组的收敛阶为一,即如二分法的收敛阶,且每一级方程组的误差估计如二分法的误差估计,我们不能求出方程组的收敛阶,我们仅能用第
级方程组的数值解,且需要求出每一级方程组的数值解,所以每一级方程组的收敛阶为一,即如二分法的收敛阶,且每一级方程组的误差估计如二分法的误差估计,我们不能求出方程组的收敛阶,我们仅能用第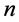 级方程组在二分法下的收敛阶近似代替原方程组的收敛阶,即为线性收敛。
级方程组在二分法下的收敛阶近似代替原方程组的收敛阶,即为线性收敛。
3.3. 解法的精度
定义3.31:一级方程式所求的数值解的精度定义为一级精度,二级方程组所求的精度定义为二级精度,即 级方程组的精度为定义
级方程组的精度为定义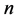 级精度,这里
级精度,这里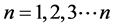 ,又有下面的标记,一级精度记为
,又有下面的标记,一级精度记为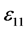 ,二级精度记为
,二级精度记为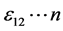 级精度记为
级精度记为 ,从以上的求数值解的过程不难发现,要想使原方程组的精度达到要求,那么必须从一级精度做起,即要求一级精度达到一定的要求,之后二级精度在一级精度的要求下达到要求,这样依次类推,达到原方程组所需要的精度,通常有下面的关系
,从以上的求数值解的过程不难发现,要想使原方程组的精度达到要求,那么必须从一级精度做起,即要求一级精度达到一定的要求,之后二级精度在一级精度的要求下达到要求,这样依次类推,达到原方程组所需要的精度,通常有下面的关系
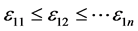 (13)
(13)
由式子(13)我们知道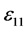 精度要足够高。
精度要足够高。
4. 实例
为了能很好的了解这种消元法,从线性方程组开始介绍
4.1. 线性方程组的实例
例1
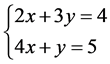 (14)
(14)
引入未知量 ,并且使
,并且使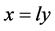 ,代入上面的方程组,可以得到下面的方程组
,代入上面的方程组,可以得到下面的方程组
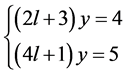 (15)
(15)
两式相除得:
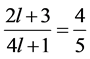 (16)
(16)
可以得到
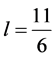 (17)
(17)
那么知道(即可以得到下面的式子)
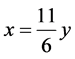 (18)
(18)
代入原方程组可以得到
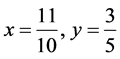 (19)
(19)
例2
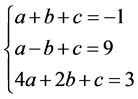 (20)
(20)
引入未知量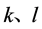 ,并且使
,并且使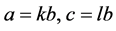 代入上面的方程组可以得到下面的方程组
代入上面的方程组可以得到下面的方程组
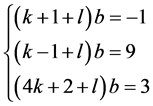 (21)
(21)
那么可以得到下面的方程组
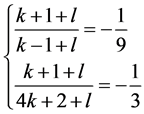 (22)
(22)
整理得:
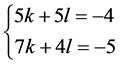 (23)
(23)
再次引入未知量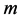 ,并且使
,并且使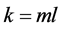 ,代入上面的式子,可以得到
,代入上面的式子,可以得到 的值。如下
的值。如下
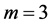
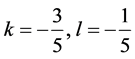
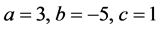
4.2. 非线性代数方程组的实例
例3
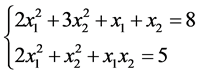 (24)
(24)
下面引入最大值符号,记为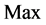 。则
。则
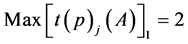 (25)
(25)
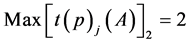 (26)
(26)
使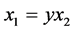 那么可以得到下面的方程组
那么可以得到下面的方程组
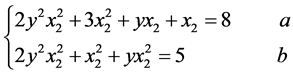 (27)
(27)
对比(25)(26)(27)会发现有如下规律
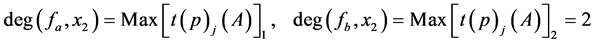
由(27)式可以得到下面的式子
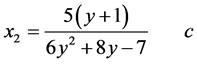 (28)
(28)
将方程式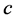 与方程式
与方程式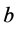 作用可以得到下面的式子
作用可以得到下面的式子
 (29)
(29)
联立(28)(29)可以得到下面的方程式
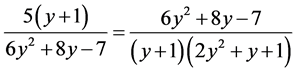 (30)
(30)
整理得
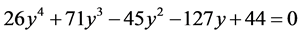 (31)
(31)
由方程式(31)可知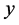 在(0,1)中必有一解,故选初值(0,1)迭代13次得
在(0,1)中必有一解,故选初值(0,1)迭代13次得 ,可知其精度
,可知其精度 代入方程组(27)中,可以的到下列方程组
代入方程组(27)中,可以的到下列方程组
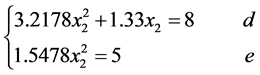
分别求出方程式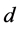 、
、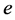 的数值解,如下:
的数值解,如下:
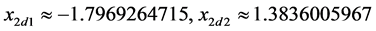
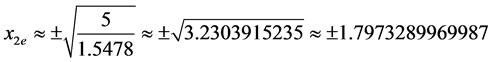
故取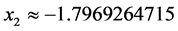 ,可知
,可知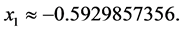
4.3. 利用牛顿法得到的数值解
看图1选初值(−1, −2),则迭代4次

5. 总结与讨论
优点:大范围收敛,即不需要选定合适的初值,而牛顿迭代法及其变形,都是小范围收敛,需要选定合适的初值,对于多元高次方程组必须凭感觉选定其合适的初值,才能有效的得到其精确的数值解,且此算法可以求出其全部的数值解,而牛顿迭代法及其变形仅能求出一个解或部分解。

Figure 1. Using the images to evaluate generally small range of 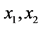
图1. 用图像来评估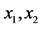 的大致小范围
的大致小范围
表1. 本文消元法与牛顿迭代法精度对比
缺点:其算法较牛顿迭代法复杂,其精度在增加迭代次数时可以达到其牛顿迭代法的精度(表1)。
致 谢
在此我要特别感谢我的数学老师朱琳对我的悉心指导,以及《应用数学进展》的老师为此文提出的宝贵的意见。
参考文献 (References)
- [1] 张平文, 李铁军 (2007) 数值分析. 北京大学出版社, 北京, 110-131.
- [2] Zhou, Y.N. (2014) A kind of proof about triangles’s congruent and a new kind of elimination method. Open Science Repository Mathematics, e23050492.
- [3] 吴文俊 (2000) 数学机械化. 科学出版社, 北京.
