设为首页 加入收藏 期刊导航 网站地图

Advances in Applied Mathematics
Vol.06 No.01(2017), Article ID:19597,8 pages
10.12677/AAM.2017.61007

High Accuracy Rendering of 3D Ship Route Using Ellipsoidal Projection

Yuanming Song1, Lian Zhou1,2, Jun Chen3

1Department of Mathematics, Shanghai Maritime University, Shanghai

2School of Mathematical Science, University of Science and Technology of China, Hefei Anhui

3Faculty of Science, Ningbo University of Technology, Ningbo Zhejiang

Received: Jan. 2nd, 2017; accepted: Jan. 17th, 2017; published: Jan. 22nd, 2017

Copyright © 2017 by authors and Hans Publishers Inc.

This work is licensed under the Creative Commons Attribution International License (CC BY).

http://creativecommons.org/licenses/by/4.0/

ABSTRACT

In order to solve the problem of 3D high accuracy rendering of ship route in electronic navigational chart, a method based on the ellipsoidal projection is presented. Firstly, the ellipsoidal projection is established, and the point on the ellipsoid is one-to-one corresponding to the point on the plane. Secondly, the port and ship position information is projected onto the plane, and a plane interpolation curve is constructed by using Hermite interpolation technique. Then using the inverse ellipsoidal projection, a curve on the earth surface is obtained. Based on the information of the ship heading, the algorithm of 3D route length optimization and multi-route intersection is presented. The automatic generation of 3D route and related calculation are realized. Finally, numerical experiments show that the method is more realistic and more accurate than the existing methods.

Keywords:Ellipsoidal Projection, Route Rendering, Electronic Navigational Chart, 3D Route

基于椭球极投影的三维船舶航线高精度绘制

宋元铭1，周联1,2，陈军3

1上海海事大学数学系，上海

2中国科学技术大学数学学院，安徽 合肥

3宁波工程学院理学院，浙江 宁波

收稿日期：2017年1月2日；录用日期：2017年1月17日；发布日期：2017年1月22日

摘 要

为解决电子海图中三维船舶航线高精度绘制问题，给出了一种基于椭球极投影的绘制方法。首先，通过建立椭球极投影，将椭球面上的点与平面上的点作一一对应。其次，将港口和船舶位置信息投影到平面上，利用Hermite插值技术，构造一条平面插值曲线。然后将该平面曲线通过椭球极逆投影，得到一条地球面曲线。最后，基于船舶航向等信息，提出了三维航线长度优化及多组航线交点求解的算法，实现了三维航线自动生成及相关计算。数值实验表明本文方法较已有方法更具真实感，精度更高。

关键词 :椭球极投影，航线绘制，电子海图，三维航线

1. 引言

电子海图是航海的重要工具之一。航线的制定、航迹的运算及数据分析都离不开海图。然而目前二维电子海图系统和其他二维地图一样，其本质都是基于抽象符号的系统，不能直观还原自然界的真实面貌且易形成抽象多义化，给使用者的辨识和符号意义还原带来困难，三维电子海图系统的研发已成为电子海图系统一个重要的研究方向 [1] 。而三维船舶航线的真实感绘制是三维电子海图系统的重要组成部分。

现有海图投影多使用墨卡托投影，在大洋航行及其他大比例尺港湾图中还采用日晷投影或高斯-克吕格投影等 [2] 。但这些海图投影方法都是将三维航线信息绘制在平面海图上，得到的是二维航线 [3] [4] 。现有的三维航线绘制方法，只是简单地将船舶的经纬度位置用直线或低次曲线进行空间样条插值 [5] 。这种绘制方法会造成航线与地球表面不贴近的情况，如图1(a)所示。

(a) (b)

Figure 1. Drawing of 3D route. (a) the existing method; (b) our method

图1. 三维航线绘制。(a) 已有方法；(b) 本文方法

为解决这种逆投影失真的现象，本文引入了椭球极投影。先将地球面上船舶航行的三维位置点全部映射到二维平面上，再用样条曲线将这些平面点插值，得到一条平面曲线。最后利用椭球极逆投影将该平面曲线投影到地球面上，得到一条与地球面完全贴合且插值原来三维船舶位置点的空间曲线。并在三维椭球面上建立有关航线长度计算及交点求解的算法，最终实现给定若干港口数据，自动生成三维航线及其长度、交点等信息。

图1为分别采用现有海图投影方式及本文提出的椭球极投影在选取相同视角时截取任意两段的效果图对比。显然采用本文中椭球极投影后的点及线段与地球面更贴近。

2. 椭球极投影

2.1. 纸型

地球形状接近于旋转椭球体，本文采用1980年国际大地测量和地球物理联合会决定采用的椭球体参数 [5] 。记地球的赤道半径a = 6378137米，极半径c = 6356752米，则地球面方程为

。 (1)

以地球南极为原点，x轴指向格林尼治子午面与地球赤道的交点，z轴指向地球北极，y轴垂直于平面xOz建立三维直角坐标系。如图2所示，北极点N坐标为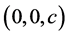。任取椭球面上除N点之外的一点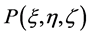，则直线NP与平面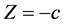：相交于点。

直线的标准方程为

，

则平面上点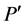的坐标可用椭球面上点的坐标来表示，

。 (2)

直线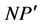的参数方程为

， (3)

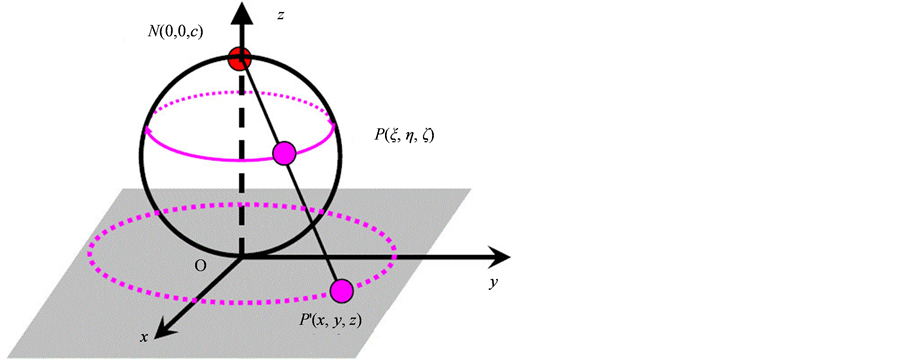
Figure 2. Ellipsoidal projection

图2. 椭球极投影

将(3)代入到(1)，则点可用点的坐标表示，

。(4)

记(2)为椭球极投影公式，(4)为椭球极逆投影公式。

3. 航线绘制

3.1. 三维投影至二维

先将船舶位置的经纬度数据进行坐标转换，得到一组三维坐标。再利用椭球极投影公式(2)，将该组地球面上的三维坐标投影到平面上，得到一组二维坐标。最后利用初始航向的导矢信息，进行三次样条插值，得到一条平面曲线。

3.2. 二维投影至三维

将所得到的平面曲线代入到椭球极逆投影公式(4)，得到椭球面曲线

4. 航线长度的计算

在已知港口经纬度信息及到达各港口的初始航向及末尾航向时下，在椭球极投影的基础上通过构造三次Bézier曲线得到三维坐标系下的各段航线的参数方程，结合曲线积分公式建立求解航线最短的规划模型。

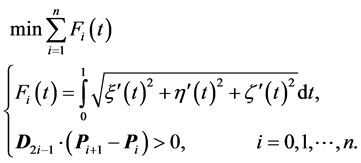
其中，目标函数为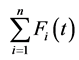，即各段航线长度之和。为决策变量，是两港口间的航向信息。为港口

坐标。通过对参量(航向信息)进行优化，求解出航线长度的最小值。

本文中的航线计算是在已选定推荐航线的前提下进行的，即已考虑航线的可行性与可操作性。实际舰船航行中，在舰船航行密度大、海区条件复杂的区域采用推荐航行更能保障安全，也更便于交通管理。当舰船走出航行复杂区后为考虑经济性，采用自动生成的优化航线。本文就使用这种推荐航线与自动生成航线相结合的使用方法，一般来说推荐航线在首尾端。但在实际情况中，航线的转向次数、转向角度都存在一定的惩罚性。故在模型的进一步优化中，可考虑增加约束条件，并采用层次分析法对限制条件进行权重分析。通过进一步处理增加自动生成航线的可操作性，使其更具现实意义。

5. 多组航线交点的求解

由于投影不影响曲线的相交关系，为简化问题，从平面上两线段的相交判断出发。先找出投影平面上的相交点再逆投影回椭球面，经过经纬度信息转换即可得到相交航线的位置信息。

为解决已知多组航线数据寻找交叉地点的问题，建立多组航线交点求解算法，这里的相交不一定是同一时空下的相交，仅代表计划航线图的可能相交点。要判断是否存在交点，首先对计划航线的轴坐标范围进行判断，首先排除若干组数据没有交集的部分。接着需要将可能区域的计划航线与周围每条线路进行相交判断。若存在交点则标出具体位置；若不存在则进行下一判断。具体如图3与图4所示。

假设计划航线1的待判断线段为的两端点坐标为、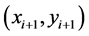，航线2的待判断线段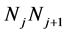的端点坐标分别为、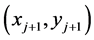，即两条直线的方程可表述为：

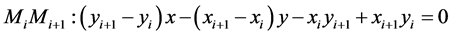
线段与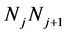相交的充分必要条件是：、两点分别位于线段两侧(或与线段重合)。将、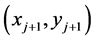分别带入的直线方程，可得到

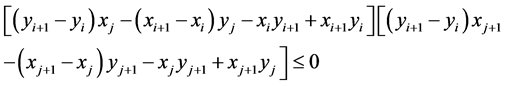
则可证明、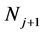两点分别位于线段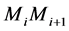的两侧，即两线段是相交关系。

时，即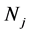、两点分别位于线段的同侧，即两线段不相交。对所有的可能线段进行这样的判断。直到所有可能点均判断完毕。

考虑到在具体航行过程中，船体自身长度也会对交点求解有所影响，所以可将误差精度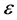设置在一定范围内，即当：

时我们就认为两航线段是相交的。

6. 数值实验

以两组各15个港口的经纬度信息为例，根据本文投影方式计算出其在三维坐标系及二维坐标系下的坐标。第一组和第二组数据所绘制航线分别如图5和图6所示。两条航线的交点如图7所示。数据1航线长度为，数据2航线长度为。还可以通过输出的分段航线长度矩阵得到任意两港口之间航线长度。交点的三维坐标是。转换后的经纬度信息为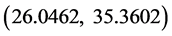，即北纬26度3分，东经35度22分。图8给出第一组数据的真实感高精度绘制。

7. 总结和展望

本文建立了椭球极投影，将地球面上的点与平面上的点一一对应。将地球面上的航海位置信息投影到平面上，得到一条相应的插值曲线。然后利用逆投影，将该平面曲线投影到地球面上。这条空间曲线

Figure 3. Relation a between two line

图3. 两线段关系a

Figure 4. Relation b between two line

图4. 两线段关系b

Figure 5. Route drawn by data 1

图5. 数据1所绘制航线

Figure 6. Route drawn by data 2

图6. 数据2所绘制航线

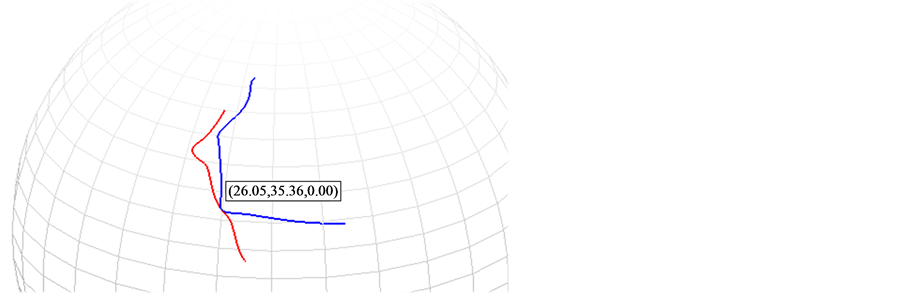
Figure 7. Route intersection using data 1 and 2

图7. 数据1与数据2的三维航线交点求解

Figure 8. Realistic rendering using data 1

图8. 数据1的真实感绘制

插值原来的航海位置信息。建立优化算法，控制港口间的航向参数，得到最佳航向及最短航线段的最优解。此外，提出一种多组航线求交算法，达到三维空间上航线的自动求交。最后算例表明本文方法的高效性。

本文利用椭球极投影从空间到平面，再回到空间的构造方法来绘制航线。未来工作可以直接从球面曲线插值的角度 [6] [7] [8] [9] ，开发椭球面曲线的形状分析和插值算法。

基金项目

国家自然科学基金项目(11401373, 11226327, 11301334)；浙江省自然科学基金(LY16F020020)。

文章引用

宋元铭,周联,陈军. 基于椭球极投影的三维船舶航线高精度绘制
High Accuracy Rendering of 3D Ship Route Using Ellipsoidal Projection[J]. 应用数学进展, 2017, 06(01): 54-61. http://dx.doi.org/10.12677/AAM.2017.61007

参考文献 (References)

  1. 1. 张立华. 基于电子海图的航线自动生成理论与方法[M]. 北京: 科学出版社, 2011.

  2. 2. 夏一行, 胡力, 周泓, 等. 电子海图应用系统中坐标变换算法的研究[J]. 工程设计学报, 2003, 10(5): 299-302.

  3. 3. 聂皓冰, 王胜正, 胡志武, 等. 航线动态优化算法在海上搜救中的应用[J]. 上海海事大学学报, 2011, 32(4): 1-6.

  4. 4. 吕超, 胡勤友, 向哲, 等. 中国沿海主要港口推荐航线算法及其实现[J]. 上海海事大学学报, 2015, 36(3): 20-23.

  5. 5. 张英俊. 电子海图的数学和算法基础[M]. 大连: 大连海事大学出版社, 2001.

  6. 6. 方雄兵. 计算机图形学中非线性投影问题的研究[D]: [博士学位论文]. 武汉: 华中科技大学, 2012.

  7. 7. Piegl, L.A. and Tiller, W. (2001) Parameterization for Surface Fitting in Reverse Engineering. Computer-Aided Design, 33, 593-603. https://doi.org/10.1016/S0010-4485(00)00103-2

  8. 8. Jüttler, B. and Wang, W.P. (2003) The Shape of Spherical Quartics. Computer Aided Geometric Design, 20, 621-636. https://doi.org/10.1016/j.cagd.2003.07.003

  9. 9. Alexandra, M., Konstantin, I. and Dmitry, C. (2014) Least-Squares Fitting of a Three-Dimensional Ellipsoid to Noisy Data. Applied Mathematical Sciences, 8, 7409-7421.

期刊菜单