Advances in Applied Mathematics
Vol.06 No.02(2017), Article ID:20005,12
pages
10.12677/AAM.2017.62018
Integration of Heterogeneous Complex Function
Yun Chen1, Xuejiao Zhao2, Jicheng Tao1
1Department of Mathematics, China Jiliang University, Hangzhou Zhejiang
2College of Liangxin, China Jiliang University, Hangzhou Zhejiang
Received: Mar. 6th, 2017; accepted: Mar. 25th, 2017; published: Mar. 28th, 2017

ABSTRACT
In this paper, we introduce the definitions of integration of heterogeneous complex function, and then discuss the property of integration heterogeneous complex function. We establish heterogeneous Cauchy integral theorem and Cauchy integral formula, and then obtain the relationship between heterogeneous complex analytic function and heterogeneous Laplace equation.
Keywords:Integration of Heterogeneous Complex Function, Heterogeneous Cauchy Integral Theorem, Heterogeneous Cauchy Integral Formula, Heterogeneous Laplace Equation
非均匀复变函数的积分
陈雲1,赵雪娇2,陶继成1
1中国计量大学应用数学系,浙江 杭州
2中国计量大学量新学院,浙江 杭州
收稿日期:2017年3月6日;录用日期:2017年3月25日;发布日期:2017年3月28日

摘 要
本文给出了非均匀复变函数积分的定义和性质,建立了非均匀Cauchy积分定理和Cauchy积分公式,并且获得了非均匀解析函数与非均匀拉普拉斯方程的关系。
关键词 :非均匀复变函数积分,非均匀Cauchy积分定理,非均匀Cauchy积分公式,非均匀拉普拉斯方程

Copyright © 2017 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 介绍
本文在文献 [1] 的基础上进一步讨论非均匀复变函数的积分理论,将会为文献 [2] [3] [4] 解决生物学的一些反应扩散模型建立更合理的数学方法。我们知道,原来的复数空间瑞士数学家欧拉在1777年系统地建立了复数理论,发现了复指数函数和三角函数间的关系,创立了复变函数论的一些基本定理,用符号“ ”
”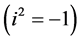 作为虚数的单位,建立了复数,随后发现复数与调和函数有密切的联系 [5] [6] [7] ,在文献 [8] [9] 建立了广义解析函数理论,这些问题自然与扩散问题也有紧密联系,从而可以用复变函数理论解扩散问题的解,但当空间非常不均匀,扩散也不均匀时,解决问题会非常繁琐,鉴于上述问题,作者们在文献 [1] 中引入非均匀复数和非均匀复变函数,并且建立了非均匀解析函数与非均匀C.-R.方程组的关系,本文在 [1] 的基础上进一步讨论非均匀复变函数的积分理论,利用这些理论讨论非均匀拉普拉斯方程的解析解。
作为虚数的单位,建立了复数,随后发现复数与调和函数有密切的联系 [5] [6] [7] ,在文献 [8] [9] 建立了广义解析函数理论,这些问题自然与扩散问题也有紧密联系,从而可以用复变函数理论解扩散问题的解,但当空间非常不均匀,扩散也不均匀时,解决问题会非常繁琐,鉴于上述问题,作者们在文献 [1] 中引入非均匀复数和非均匀复变函数,并且建立了非均匀解析函数与非均匀C.-R.方程组的关系,本文在 [1] 的基础上进一步讨论非均匀复变函数的积分理论,利用这些理论讨论非均匀拉普拉斯方程的解析解。
2. 预备知识
下面给出非均匀复数、非均匀复变函数的一些基本定义及性质,具体参考文献 [1] 。
2.1. 非均匀复数的定义
考虑到复数在各个领域的广泛应用,我们对复数单位做进一步推广,定义非均匀复数。
定义集合 ,其中
,其中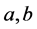 为实数
为实数 ,
, 。
。
在 中引入数乘
中引入数乘

在 中引入加法
中引入加法
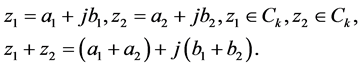
定理 2.1在上式数乘和加法运算下,Ck为R上的一个线性空间。
定理2.2 为
为 上的一个域。
上的一个域。
2.2. 非均匀复变函数的定义及性质
非均匀复变函数的定义,类似于复变函数的定义,形式上和数学分析中函数定义相同,此时自变量和函数的取值均为新定义的非均匀复数。在定义函数之前,根据复平面点集的几个基本概念,我们可以推广到非均匀复平面上。
定义2.1由 由不等式所确定的平面点集(简称点集),就是以
由不等式所确定的平面点集(简称点集),就是以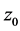 为圆心,以
为圆心,以 为半径的圆,称为点
为半径的圆,称为点 的
的 邻域。
邻域。
注2.1:考虑点集E,同样也有聚点或极限点、孤立点、外点、闭集、内点、开集、边界点、边界的概念,与复变平面定义相同,在此不再一一赘述。
定义2.2设f:从Ck到Ck的映射,则称为f为Ck上的非均匀复函数。
非均匀函数的导数,解析的定义及与偏微分方程组的关系在文献 [1] 中给出,本文在下面给出结论:
定义2.3 设函数 于点集
于点集 上有定义,
上有定义, 为
为 的聚点,若存在非均匀复数
的聚点,若存在非均匀复数 ,对任给的
,对任给的 ,有
,有 ,只要
,只要 ,就有
,就有

则称函数 沿
沿 于
于 有极限
有极限 ,并记为
,并记为

定义2.4 设函数 于点集
于点集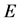 上有定义,
上有定义, 为
为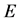 的聚点,且
的聚点,且 ,若
,若

即对任给的 ,有
,有 ,只要
,只要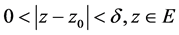 ,就有
,就有

则称函数 沿
沿 于
于 连续。
连续。
2.3. 非均匀复变函数的导数
定义2.5 设函数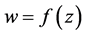 在点
在点 的邻域内或者包含
的邻域内或者包含 的区域
的区域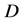 内有定义,考虑比值
内有定义,考虑比值

如果当 按照任意方式趋于
按照任意方式趋于 时,即当
时,即当 按照任意方式趋于0时,比值
按照任意方式趋于0时,比值 的极限都存在,且其值有限,则称此极限为函数
的极限都存在,且其值有限,则称此极限为函数 在
在 的导数,并记为
的导数,并记为 ,即
,即

这时称函数 于点
于点 可导。
可导。
设函数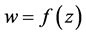 在点
在点 可导,于是
可导,于是

即是

其中 为比
为比 高阶无穷小。
高阶无穷小。
我们称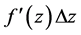 为
为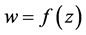 在点
在点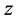 的微分,记为
的微分,记为 或者
或者 ,此时也称
,此时也称 在点
在点 可微,即
可微,即
 .
.
特别,当 时,
时, ,于是上式为
,于是上式为 ,即
,即

由此可见, 在
在 处可导与
处可导与 在
在 处可微是等价的。
处可微是等价的。
2.4. 非均匀复变函数的解析性
定义2.6 如果函数 在区域
在区域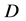 内可微,则称
内可微,则称 为区域
为区域 内的解析函数,或称函数
内的解析函数,或称函数 在区域
在区域 内解析。函数在某点解析,是指在该点的某一个邻域内是解析的:函数在某个闭域解析,是指在包含该闭域的某区域内解析。
内解析。函数在某点解析,是指在该点的某一个邻域内是解析的:函数在某个闭域解析,是指在包含该闭域的某区域内解析。
定理2.3 设函数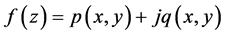 在区域
在区域 内有定义,且在
内有定义,且在 内一点
内一点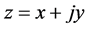 可微,则必有
可微,则必有
1) 偏微分 在点
在点 连续;
连续;
2) 在点
在点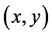 满足非均匀C.-R.方程。
满足非均匀C.-R.方程。
而且这是可微的必要条件,并非充分的。
定理2.4 设函数 在区域
在区域 内解析,则
内解析,则
1) 二元函数 在区域
在区域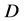 内解析;
内解析;
2)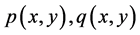 在区域
在区域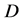 内满足非均匀C.-R.方程。
内满足非均匀C.-R.方程。
定理2.5 设函数 在区域
在区域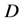 内解析,则
内解析,则
1) 偏微分 在区域
在区域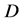 内连续;
内连续;
2) 在区域
在区域 内满足非均匀C.-R.方程。
内满足非均匀C.-R.方程。
这也是可微的充要条件。
其中非均匀C.-R.方程为:

3. 非均匀复积分的概念及基本性质
3.1. 非均匀复变函数积分的定义
定义3.1设非均匀复数域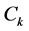 上的有向曲线
上的有向曲线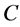 :
:

以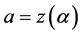 为起点,
为起点,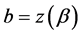 为终点,
为终点, 沿
沿 有定义,顺着
有定义,顺着 从
从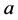 到
到 的方向在
的方向在 上取分点:
上取分点: ,这样可以将曲线
,这样可以将曲线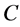 划分为
划分为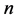 个弧段,在从
个弧段,在从 到
到 的每一个弧段上任取一点
的每一个弧段上任取一点 ,那么
,那么

当分点增多时,弧段逐渐加细,如果和数 极限存在且为S,则称
极限存在且为S,则称 沿
沿 (从
(从 到
到 )可积,
)可积, 为其上的积分,记号为
为其上的积分,记号为 ,其中
,其中 为积分路径。
为积分路径。
定理3.1若函数 沿曲线
沿曲线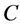 连续,则该函数沿曲线
连续,则该函数沿曲线 可积,且
可积,且
 .(3.1)
.(3.1)
证明:设
 ,
, 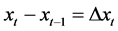 ,
,  ,
,
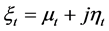 ,
,  ,
,  ,
,
则

右端的两个和数是对应的两个曲线积分的积分和数。在定理连续条件下,函数的实部和虚部必沿曲线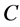 连续,于是这两个曲线积分都是存在的。因此,积分
连续,于是这两个曲线积分都是存在的。因此,积分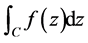 存在。
存在。
例3.1 令 是非均匀复数域
是非均匀复数域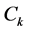 上的表示连接点
上的表示连接点 及
及 的任一曲线,证明:
的任一曲线,证明:
1) ;2)
;2) 。
。
证明:
1) 注意到: ,由定义可知
,由定义可知 ,为定值,只与起点和终点有关,从而
,为定值,只与起点和终点有关,从而 。
。
2) 因 ,首先选
,首先选 ,则得
,则得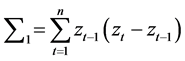 ,
,
又选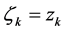 ,则得
,则得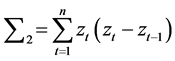 ,
,
由定理3.1可知积分 存在,因而
存在,因而 的极限存在,且应与
的极限存在,且应与 及
及 的极限相等,
的极限相等,
从而应与 的极限相等。
的极限相等。
令 ,所以
,所以 。
。
3.2. 非均匀复变函数积分的计算问题
设有非均匀复数域 上的光滑曲线
上的光滑曲线 :
:
 ,
,
这就表示 在
在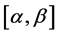 上连续且有不为零的导数
上连续且有不为零的导数 ,又设
,又设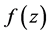 沿
沿 连续,令
连续,令
 ,
,
根据式(3.1)
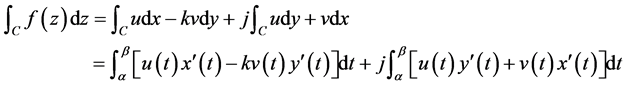
即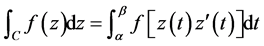
例3.2 证明 ,
,
其中,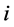 为复数单位,
为复数单位,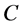 表示以
表示以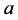 为心,
为心, 为半径的圆周。
为半径的圆周。
证明:设圆周 参数方程为:
参数方程为: ,
, 。
。

下面我们利用留数定理可以证明它的值是 。令
。令 ,则,
,则,

因此有,
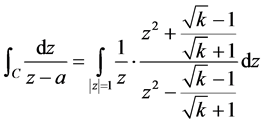
在 分别讨论,利用留数定理得
分别讨论,利用留数定理得
注3.1:当 时,我们获得的结论与复变函数中的结论是一致的,那么当
时,我们获得的结论与复变函数中的结论是一致的,那么当 为其它自然数结论是否与复变函数中的结论一致呢?有兴趣的读者可以利用留数理论讨论。
为其它自然数结论是否与复变函数中的结论一致呢?有兴趣的读者可以利用留数理论讨论。
3.3. 非均匀复积分的基本性质
设函数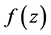 ,
,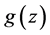 沿曲线
沿曲线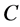 连续,我们可以得到以下基本性质:
连续,我们可以得到以下基本性质:
1)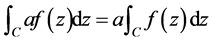 ,
,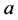 是复常数;
是复常数;
2) ;
;
3) ,其中
,其中 由曲线
由曲线 衔接而成;
衔接而成;
4) ;
;
5) 。
。
4. 非均匀复变函数的柯西积分定理
4.1. 非均匀柯西积分定理
我们在上一节例题3.1中,可以发现被积函数在非均匀复数域 上的单连通区域
上的单连通区域 内处处解析,则积分与路径无关,或者说沿区域
内处处解析,则积分与路径无关,或者说沿区域 内任何闭曲线的积分为零;而例题3.2中,被积函数有奇点
内任何闭曲线的积分为零;而例题3.2中,被积函数有奇点 ,也就是说,被积函数
,也就是说,被积函数 平面上除去点
平面上除去点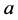 后的非单连通区域内处处解析,积分结果为
后的非单连通区域内处处解析,积分结果为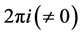 ,
, 是圆周,从而说明在此区域内积分与路径有关。
是圆周,从而说明在此区域内积分与路径有关。
由此可见,非均匀复积分值与路径无关的条件,或沿区域内任何闭曲线积分值为0的条件,可能与被积函数的解析性及解析区域的单连通性有关。
1825年法国著名数学家柯西给出研究复变函数的钥匙——柯西积分定理,经过验证,该定理同样适用非均匀复变函数 情形。为了做一些区分,我们称为非均匀柯西积分定理。
情形。为了做一些区分,我们称为非均匀柯西积分定理。
定理4.1 设函数 在非均匀复数域
在非均匀复数域 上的单连通区域
上的单连通区域 内解析,
内解析, 为
为 内任一条周线,则
内任一条周线,则
 .
.
直接证明该定理是有困难的,从德国数学家黎曼对原柯西积分定理的证明角度出发,我们在附加假设“ 在区域
在区域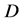 内连续”的条件下,得到简单证明。
内连续”的条件下,得到简单证明。
借助黎曼证明:令 ,
, ,由公式(3.1),
,由公式(3.1),
 ,
,
在附加条件下,偏导数 ,
,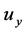 ,
,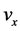 ,
, 在区域
在区域 内连续,由非均匀复变函数C.-R.方程(参见文献 [1] ):
内连续,由非均匀复变函数C.-R.方程(参见文献 [1] ):
 ,
,  ,
,
再由格林定理,
 ,
,  ,
,
故得
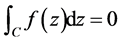 .
.
由定理4.1,可以得到
定理4.2设函数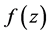 在非均匀复数域
在非均匀复数域 上的单连通区域
上的单连通区域 内解析,
内解析, 为
为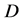 内任一条闭曲线(不必是简单的),则
内任一条闭曲线(不必是简单的),则
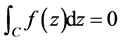 .
.
证明:因为任意闭曲线 总是可以看成区域
总是可以看成区域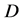 内很多条周线衔接而成,由非均匀复积分基本性质及非均匀柯西积分定理4.1,即可证明。
内很多条周线衔接而成,由非均匀复积分基本性质及非均匀柯西积分定理4.1,即可证明。
推论4.3 设函数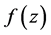 在
在 平面上的单连通区域
平面上的单连通区域 内解析,则
内解析,则 在
在 内积分与路径无关,即对
内积分与路径无关,即对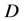 内任意两点
内任意两点 与
与 ,积分
,积分 之值,不依赖于
之值,不依赖于 内连接起点
内连接起点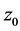 与终点
与终点 的曲线。
的曲线。
证明:不妨假设在区域 内有任意两条连接起点
内有任意两条连接起点 与终点
与终点 的曲线
的曲线 与
与 ,定义曲线
,定义曲线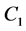 的方向为正方向,则正方向曲线
的方向为正方向,则正方向曲线 与负方向曲线
与负方向曲线 就衔接成
就衔接成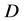 内的一条闭曲线
内的一条闭曲线 。由定理4.2与非均匀复积分的基本性质,有
。由定理4.2与非均匀复积分的基本性质,有
 ,
,
因而
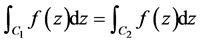 .
.
4.2. 不定积分
在4.1节中,非均匀柯西积分定理说明了积分与路径无关。也就是说,若函数 在
在 平面上的单连通区域
平面上的单连通区域 内解析,则沿
内解析,则沿 内任意曲线
内任意曲线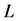 的积分
的积分 只与其起点和终点有关,当起点
只与其起点和终点有关,当起点 固定时,积分在
固定时,积分在 内定义了一个变上限
内定义了一个变上限 的单值函数,我们把它记成变上限积分
的单值函数,我们把它记成变上限积分
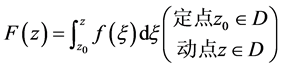 . (4.1)
. (4.1)
定理4.4 设函数 在
在 平面上的单连通区域
平面上的单连通区域 内解析,则由式(4.1)定义的函数
内解析,则由式(4.1)定义的函数 在
在 内解析,且
内解析,且 。
。
定理4.5 设
1) 函数 在单连通区域
在单连通区域 内连续;
内连续;
2)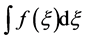 沿区域
沿区域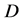 内任一周线的积分值为零,则函数
内任一周线的积分值为零,则函数
 (为内一定点)
(为内一定点)
在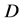 内解析,且
内解析,且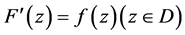 。
。
定义4.1在区域 内,如果函数
内,如果函数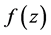 连续,则称符合条件
连续,则称符合条件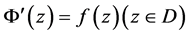 的函数
的函数 为
为 的一个不定积分或原函数,且
的一个不定积分或原函数,且 在区域
在区域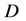 内解析。
内解析。
如果在定理4.4或者定理4.5的条件下,式(4.1)应该就是函数 的一个原函数。这一系列原函数可以表示为:
的一个原函数。这一系列原函数可以表示为:
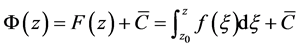 ,其中
,其中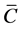 为常数 (4.2)
为常数 (4.2)
定理4.6在定理4.4或者定理4.5的条件下,若 为函数
为函数 在单连通区域
在单连通区域 内的一个任一原函数,则
内的一个任一原函数,则
 (4.3)
(4.3)
定理4.6与积分基本定理,即牛顿–莱布尼兹公式,类似。
例4.1 在单连通区域 内:
内: 内,函数
内,函数 是
是 的一个原函数,而
的一个原函数,而 在单连通区域
在单连通区域 内解析,故根据定理4.6有
内解析,故根据定理4.6有
 .
.
4.3. 非均匀柯西积分公式
根据非均匀柯西积分定理,我们可以导出对应的非均匀柯西积分公式。
定理4.7 设区域 的边界是周线(复周线)
的边界是周线(复周线) ,函数
,函数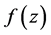 在
在 内解析,在
内解析,在 上连续,则有
上连续,则有
 (4.4)
(4.4)
证明:任意固定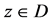 ,
, 作为
作为 的函数在区域
的函数在区域 内除点
内除点 外均解析。今以点
外均解析。今以点 为心,充分小的
为心,充分小的 为半径作圆周
为半径作圆周 ,使得
,使得 及其内部均含于
及其内部均含于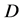 。对于复周线
。对于复周线 及函数
及函数 ,有
,有
 .
.
因此我们只需要证明
 . (4.5)
. (4.5)
在第三节例题3.2中,当 时,
时, ,那么
,那么
 (4.6)
(4.6)
根据 的连续性,写成
的连续性,写成 语言形式,即对任给的
语言形式,即对任给的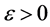 ,存在
,存在 ,只要
,只要 ,就有
,就有

从而式(4.6)不超过 ,式(4.5)得证。
,式(4.5)得证。
定义4.2 在定理4.7条件下, 称为非均匀柯西积分。
称为非均匀柯西积分。
此外,式(4.4)又可写为
 (4.7)
(4.7)
在定理4.7下,我们将式(4.4)对 求导,得到
求导,得到
 ,(4.8)
,(4.8)
继续求导,可以得到
 , (4.9)
, (4.9)
如此下去,可得下面定理。
定理4.8 在定理4.7的条件下,函数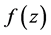 在区域
在区域 内有各阶导数,且
内有各阶导数,且
 . (4.10)
. (4.10)
式(4.10)也可以表示为
 .(4.11)
.(4.11)
例4.2 计算积分
 ,其中
,其中 。
。
解:因 在
在 上是解析的,满足柯西积分公式定理条件,再利用式(4.11),得
上是解析的,满足柯西积分公式定理条件,再利用式(4.11),得
 .
.
5. 非均匀解析函数与非均匀调和函数的关系
在4.3节中,我们知道了在区域 内解析的函数有各阶导数,从而其虚部和实部都应有二阶连续偏导数。这里,我们可以将判断函数解析的一个充分条件弱化为充要条件。
内解析的函数有各阶导数,从而其虚部和实部都应有二阶连续偏导数。这里,我们可以将判断函数解析的一个充分条件弱化为充要条件。
定理5.1 函数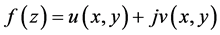 在区域
在区域 内解析的充要条件是:
内解析的充要条件是:
1) ,
,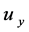 ,
, ,
, 在
在 内连续;
内连续;
2) ,
, 在
在 内满足非均匀C.-R.方程。
内满足非均匀C.-R.方程。
证明:
充分性 显然;
必要性 条件(2)的必要性显然;条件(1)因解析函数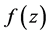 的无穷可微性,
的无穷可微性, 必在
必在 内连续,从而
内连续,从而 ,
, ,
, ,
, 在
在 内连续。
内连续。
不妨设 在区域
在区域 内解析,则由非均匀C.-R.方程 [1] 可知
内解析,则由非均匀C.-R.方程 [1] 可知
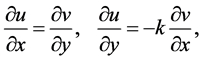
则

因 与
与 在区域
在区域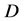 内连续,必定相等,故在区域
内连续,必定相等,故在区域 内有
内有
 (5.1)
(5.1)
同理可得
 (5.2)
(5.2)
这里与拉普拉斯方程有所区别,即非均匀复变函数下,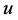 与
与 不再满足拉普拉斯方程,我们定义一种新的算子:
不再满足拉普拉斯方程,我们定义一种新的算子: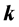 算子,运算符号为
算子,运算符号为 ;
; 与
与 满足式(5.1)和(5.2),称
满足式(5.1)和(5.2),称 与
与 满足系数为
满足系数为 的非均匀拉普拉斯方程。
的非均匀拉普拉斯方程。
定义5.1如果二元实函数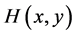 在区域
在区域 内有二阶连续偏导数,且满足非均匀拉普拉斯方程,则称
内有二阶连续偏导数,且满足非均匀拉普拉斯方程,则称 为区域
为区域 内的系数为
内的系数为 的非均匀调和函数。
的非均匀调和函数。
定义5.2 在区域 内满足非均匀C.-R.方程的两个非均匀调和函数
内满足非均匀C.-R.方程的两个非均匀调和函数 、
、 中,
中, 称为
称为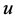 在区域
在区域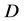 内的系数为
内的系数为 的非均匀共轭调和函数。
的非均匀共轭调和函数。
根据上面的讨论,我们得出下面定理:
定理5.2若 在区域
在区域 内非均匀解析,则在区域
内非均匀解析,则在区域 内
内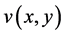 必为
必为 的系数为
的系数为 非均匀共轭调和函数。
非均匀共轭调和函数。
自然我们会想定理反过来是否成立,显然结论是不一定的。
若要 在区域
在区域 内非均匀解析,
内非均匀解析, 与
与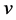 还必须满足非均匀C.-R.方程。由此,在已知某解析函数实部或虚部下就可以求出其虚部或实部。
还必须满足非均匀C.-R.方程。由此,在已知某解析函数实部或虚部下就可以求出其虚部或实部。
假设 是一个单连通区域,
是一个单连通区域, 是区域内的系数为
是区域内的系数为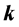 的非均匀调和函数,则其在区域内有二阶连续偏导数,由式(5.1)可知
的非均匀调和函数,则其在区域内有二阶连续偏导数,由式(5.1)可知
 (5.3)
(5.3)
在数学分析中,表达式 是全微分,那么
是全微分,那么
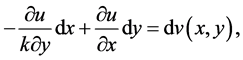 (5.4)
(5.4)
则
 (5.5)
(5.5)
类似地,
 (5.6)
(5.6)
 (5.7)
(5.7)
其中 是区域内的定点,在选取时,可以选择原点(0,0)这是因为单连通区域含原点;
是区域内的定点,在选取时,可以选择原点(0,0)这是因为单连通区域含原点; 是区域内的动点,
是区域内的动点, 和
和 是常数,积分与路径无关。
是常数,积分与路径无关。
由于任一个二元调和函数都可作为一个解析函数的实部或虚部,而虚部或实部自然可以由非均匀C.-R.方程确定,且得到的函数非均匀解析。可以得到下述定理。
定理5.3设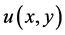 是在单连通区域
是在单连通区域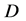 内的非均匀调和函数,根据式(5.5)可以确定出一个
内的非均匀调和函数,根据式(5.5)可以确定出一个 ,从而由
,从而由 与
与 确定出的
确定出的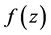 是区域
是区域 内的非均匀解析函数。
内的非均匀解析函数。
例5.1 验证 (
( 为非零实数)是
为非零实数)是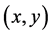 平面上的系数为
平面上的系数为 的调和函数,并求以
的调和函数,并求以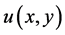 为实部的非均匀解析函数
为实部的非均匀解析函数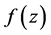 ,使满足
,使满足 。
。
解:在 平面上任意一点,
平面上任意一点,
 ,
, 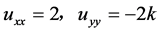
满足: ,故
,故 为
为 平面上的系数为
平面上的系数为 的非均匀调和函数。
的非均匀调和函数。
根据非均匀C.-R.方程,可知 ,
,
根据式(5.4)和(5.5),得出 ,从而
,从而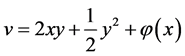 ,
,
对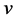 求
求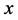 偏导,
偏导,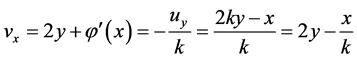 ,得出
,得出 ,从而
,从而 。
。
因此 。
。
那么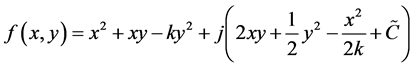 ,这是通解,代入已知条件,可以得到一个满足条件的特解:
,这是通解,代入已知条件,可以得到一个满足条件的特解: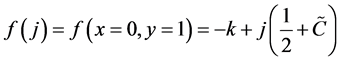 ,那么
,那么 ,故
,故
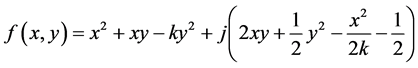 .
.
6. 结论
本文在文献 [1] 的基础上继续研究非均匀复变函数的积分,获得了解析函数的非均匀Cauchy积分公式和非均匀积分定理,建立了解析函数与非均匀调和的关系。还有很多进一步讨论的内容,如何建立非均匀复函数的泰勒展开和洛朗展开,奇点的分类,类似的留数定理;以及在物理,力学的应用。
基金项目
中国计量大学第十九届学生科研计划项目资助。浙江省自然科学基金资助,项目编号:LY16A010009。
文章引用
陈雲,赵雪娇,陶继成. 非均匀复变函数的积分
Integration of Heterogeneous Complex Function[J]. 应用数学进展, 2017, 06(02): 153-164. http://dx.doi.org/10.12677/AAM.2017.62018
参考文献 (References)
- 1. 赵雪娇, 陈雲, 陶继成. 非均匀复数和非均匀复变函数[J]. 应用数学进展, 2017, 6(1): 69-77.
- 2. 楼元. 空间生态学中的一些反应扩散方程模型[J]. 中国科学: 数学, 2015, 45(10): 1619-1634.
- 3. Allen, L., Bolker, B., Lou, Y., et al. (2007) Asymptotic Profile of the Steady States for an SIS Epidemic Patch Model. SIAM Journal on Applied Mathematics, 67, 1283-1309. https://doi.org/10.1137/060672522
- 4. Wang, W. and Zhao, X.Q. (2011) A Nonlocal and Time-Delayed Reaction-Diffusion Model of Dengue Transmission. SIAM Journal on Applied Mathematics, 71, 147-169. https://doi.org/10.1137/090775890
- 5. 李忠. 复分析导引[M]. 北京: 北京大学出版社, 2004.
- 6. 钟玉泉. 复变函数论[M]. 北京: 高等教育出版社, 2012.
- 7. 钟玉泉. 解析函数的单叶半径[J]. 四川大学学报(自然科学版), 1991, 28(4): 545-547.
- 8. 胡庆平. 广义复变函数论(I) [J]. 西北大学学报(自然科学版), 1984(2): 117-119.
- 9. 濮德潜. 广义复数上的函数[J]. 纯粹数学与应用数学, 1991(2): 69-79.