BiCR算法求解Sylvester矩阵方程组的Perhermitian解 The BiCR Algorithm for Solving the Perhermitian Solutions of Sylvester Matrix Equations

doi:10.12677/AAM.2023.1212489

Advances in Applied Mathematics
Vol. 12 No. 12 ( 2023 ), Article ID: 76957 , 20 pages
10.12677/AAM.2023.1212489

BiCR算法求解Sylvester矩阵方程组的Perhermitian解

唐孝伟^*，李胜坤

●How to Cite this Article

成都信息工程大学应用数学学院，四川成都

收稿日期：2023年11月7日；录用日期：2023年12月1日；发布日期：2023年12月12日

摘要

对于给定的矩阵 $X \in ℂ^{n \times n}$ ，如果 $S X S = S^{H}$ ，其中S是给定的反射矩阵，即 $S^{H} = S$ ， $S^{2} = I$ ，则称矩阵X为perhermitian矩阵。本文提出一种用于求解Sylvester矩阵方程组的perhermitian解的双共轭残差(BiCR)算法，并且证明了该算法的收敛性。通过选择任意初始perhermitian矩阵，可以在有限步求解出Sylvester矩阵方程组的唯一最小范数perhermitian解。最后，我们给出了一些数值算例来验证该算法的有效性和可行性。

关键词

Sylvester矩阵方程组，BiCR算法，Perhermitian解，最小范数Perhermitian解

The BiCR Algorithm for Solving the Perhermitian Solutions of Sylvester Matrix Equations

Xiaowei Tang^*, Shengkun Li

College of Applied Mathematics, Chengdu University of Information Technology, Chengdu Sichuan

Received: Nov. 7^th, 2023; accepted: Dec. 1^st, 2023; published: Dec. 12^th, 2023

ABSTRACT

For a given matrix $X \in ℂ^{n \times n}$ , matrix X is said to be perhermitian if $S X S = S^{H}$ , where S is a given reflection matrix, i.e., $S^{H} = S$ , $S^{2} = I$ . In this paper, we propose the Bi-Conjugate Residual (BiCR) algorithm for solving the perhermitian solutions of Sylvester matrix equations and prove the convergence of the algorithm. By choosing any initial perhermitian matrices, the unique minimum-norm perhermitian solutions of the Sylvester matrix equations can be solved in finite steps. Finally, we give some numerical examples to verify the validity and feasibility of the algorithm.

Keywords:Sylvester Matrix Equations, BiCR Algorithm, Perhermitian Solution, Minimum-Norm Perhermitian Solution

This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).

http://creativecommons.org/licenses/by/4.0/

1. 引言

矩阵方程在控制理论 [1] 、系统理论 [2] 和应用数学 [3] 等许多领域都有重要的作用，比如Sylvester矩阵方程可以用来恢复缺失或者损坏的信号或图像 [4] ，也可以用来研究线性时不变系统的稳定性 [5] 。另外，五点差分格式求解椭圆方程时会遇到Sylvester矩阵方程 [6] ，在常微分方程定性理论研究及数值求解的隐式Runge-Kwutta方法与块方法也会涉及到Sylvester矩阵方程 [6] 。对于它的一般解，基于Arnoldi过程，Hu等人 [7] 给出了求解 $A X - X B = C$ 的Galerkin算法和最小残差法(MINRES)；基于块Arnoldi过程，El Guennouni A等人 [8] 给出了求解 $A X - X B = C$ 的块GMRES方法(BGMRES)；为了提高收敛速度和缩短运算时间，基于全局Arnoldi过程，Fatemeh Panjeh Ali Beika等人 [9] 提出了求解Sylvester矩阵方程组的全局完全正交化方法(Gl-FOM)和全局极小残量法(Gl-GMRES)。由于Krylov子空间方法的收敛速度依赖于方程系数矩阵谱的性质，选取合适的预条件矩阵，往往可以提高收敛速度，为了进一步提高算法的收敛速度，Bouhamidi A等人 [10] 给出了预条件块Arnoldi方法求解Sylvester矩阵方程，Kaabi [11] 等人提出了预条件Galerkin算法(PGal)和预条件最小残差法(PMR)求解Sylvester矩阵方程。基于预条件全局Arnoldi过程，徐冬梅等人 [12] 给出了求解Sylvester矩阵方程组的预条件全局正交化方法(PG-FOM)和预条件全局极小残量法(PG-GMRES)。对于约束解，Dehghan和Hajarian [13] [14] 提出了求解广义Sylvester矩阵方程组的自反解和广义双对称解的CGNE方法。Dehghan和Hajarian [15] [16] 也通过推广CGNE方法得到了一般矩阵方程组的解和广义双对称解。但是，一般情况下，CGNE方法收敛速度较慢。最近，吕长青等人 [17] 和Masoud Hajarian [18] 提出了利用BiCR算法求解广义Sylvester矩阵方程组的中心对称解和反中心对称解，证明了这种BiCR算法可以在有限步内找到广义Sylvester矩阵方程组的中心对称解，并且选取特定的初始矩阵，可以得到最小范数解；闫同新等人 [19] 提出了利用BiCR算法求解广义Sylvester矩阵方程组的自反解和反自反解以及最小Frobenius范数对称解；Masoud Hajarian [18] 提出了利用BiCR算法求解广义Sylvester矩阵方程组的对称解，收敛性分析表明，BiCR算法在不存在舍入误差的情况下，可以在有限次迭代内计算出广义Sylvester矩阵方程组的最小Frobenius范数对称解对。然而，Sylvester矩阵方程组的perhermitian解目前还没有被研究过。因此，本文将给出求解Sylvester矩阵方程组的perhermitian解的BiCR算法。

在本文中，考虑如下Sylvester矩阵方程组

$\sum_{j = 1}^{q} A_{i j} X_{j} B_{i j} = C_{i}, i = 1, 2, \dots, p,$ (1.1)

其中，已知系数矩阵 $A_{i j} \in ℂ^{m \times n}, B_{i j} \in ℂ^{n \times l}$ 和常数矩阵 $C_{i} \in ℂ^{m \times l}$ ， $X_{j} \in ℂ^{n \times n}$ 是未知矩阵。

2. 预备知识

定义2.1 [20] [21] 对给定的反射矩阵 $S \in ℂ^{n \times n}$ ，即 $S^{H} = S$ ， $S^{2} = I_{n}$ 。如果矩阵 $X \in ℂ^{n \times n}$ 满足条件 $S X S = S^{H}$ ( $S X S = - S^{H}$ )，那么称其为反射矩阵S的perhermitian矩阵(skew-perhermitian矩阵)，记为 $X \in ℙ ℂ^{n \times n}$ ( $X \in S ℙ ℂ^{n \times n}$ )。

定义2.2 [22] [23] 设任意 $X, Y \in ℂ^{m \times n}$ ，规定

$〈 X, Y 〉 = Re [t r (X^{H} Y)],$

则称 $〈 X, Y 〉$ 为矩阵 $X, Y$ 的实内积，记作 $(ℂ^{m \times n}, ℝ, 〈 \cdot, \cdot 〉)$ 。

定义2.3 [22] [23] 设矩阵 $X \in ℂ^{n \times n}$ ，规定

$‖ X ‖ = \sqrt{〈 X, X 〉} = \sqrt{Re [t r (X^{H} X)]},$

则称 $‖ X ‖$ 为矩阵X的Frobenius范数，简称F范数。

定义2.4 [22] [23] 设矩阵 $X, Y \in ℂ^{n \times n}$ ，如果 $〈 X, Y 〉 = 0$ ，那么矩阵 $X, Y$ 是正交的。

引理2.1 设矩阵 $X, Y \in M_{n} (ℂ)$ ，有

$Re [t r (X Y)] = Re [t r (\bar{X Y})] = Re [t r (Y X)] = Re [t r (X^{T} Y^{T})] = Re [t r (X^{H} Y^{H})] .$

引理2.2 设矩阵 $X \in ℙ ℂ^{n \times n}, Y \in S ℙ ℂ^{n \times n}$ ，则矩阵 $X, Y$ 是正交的。

证明：因为

$\begin{matrix} 〈 X, Y 〉 = Re [t r (X^{H} Y)] = - Re [t r (S X S \cdot S Y^{H} S)] = - Re [t r (X Y^{H})] \\ = - Re [t r {(X Y^{H})}^{H}] = - Re [t r (Y X^{H})] = - Re [t r (X^{H} Y)] \\ = - 〈 X, Y 〉, \end{matrix}$

所以 $〈 X, Y 〉 = 0$ ，因此矩阵 $X, Y$ 正交。 □

引理2.3 设矩阵 $X \in ℂ^{n \times n}$ ，那么 $X + S X^{H} S \in ℙ ℂ^{n \times n}$ 。

证明：因为

$S (X + S X^{H} S) S = S X S + X^{H} = {(X + S X^{H} S)}^{H},$

所以结论成立。 □

根据引理2.3，我们可以很容易地构造一个perhermitian矩阵。

引理2.4 设矩阵 $X \in ℙ ℂ^{n \times n}$ ， $Y \in ℂ^{n \times n}$ ， $S \in ℂ^{n \times n}$ 为反射矩阵，有

$\frac{1}{2} Re (t r (X^{H} (Y + S Y^{H} S))) = Re (t r (X^{H} Y)) .$

证明：

$\begin{matrix} \frac{1}{2} Re (t r (X^{H} (Y + S Y^{H} S))) = \frac{1}{2} (Re (t r (X^{H} Y)) + Re (t r (X^{H} S Y^{H} S))) \\ = \frac{1}{2} (Re (t r (X^{H} Y)) + Re (t r (S X^{H} S Y^{H}))) \\ = \frac{1}{2} (Re (t r (X^{H} Y)) + Re (t r (X Y^{H}))) \\ = \frac{1}{2} (Re (t r (X^{H} Y)) + Re (t r {(Y X^{H})}^{H})) \end{matrix}$

$\begin{matrix} = \frac{1}{2} (Re (t r (X^{H} Y)) + Re (t r (Y X^{H}))) \\ = \frac{1}{2} (Re (t r (X^{H} Y)) + Re (t r (X^{H} Y))) \\ = Re (t r (X^{H} Y)) . \end{matrix}$

证毕。 □

引理2.5 如果矩阵 $X, Y \in ℙ ℂ^{n \times n}$ ， $α, β \in ℝ$ ，那么 $α X + β Y \in ℙ ℂ^{n \times n}$ ，换句话说， $ℙ ℂ^{n \times n}$ 是 $ℂ^{n \times n}$ 的一个子空间。

证明：因为

$S (α X + β Y) S = α S X S + β S Y S = α X^{H} + β Y^{H} = {(α X + β Y)}^{H} .$

证毕。 □

3. 迭代方法

在这个部分，我们提出一种用于求解Sylvester矩阵方程组的perhermitian解的BiCR算法。

3.1. BiCR算法求解Sylvester矩阵方程组的Perhermitian解(表1)

首先，给出该算法的迭代过程。

Table 1. TheBiCR algorithm for solving the perhermitian solutions of the matrix equations (1.1)

表1. BiCR算法求解矩阵方程组(1.1)的perhermitian解

通过算法3.1，我们可以知道 $X_{j} (k), W_{j} (k), U_{j} (k)$ 和 ${\tilde{U}}_{j} (k)$ 都是反射矩阵S的perhermitian矩阵， $X_{j} (k) \in ℙ ℂ^{n \times n}$ ， $W_{j} (k) \in ℙ ℂ^{n \times n}$ ， $U_{j} (k) \in ℙ ℂ^{n \times n}$ ， ${\tilde{U}}_{j} (k) \in ℙ ℂ^{n \times n}$ ，其中 $j = 1, 2, \dots, q$ 。

3.2. 收敛性分析

接下来，对该算法进行收敛性分析。我们可以通过以下定理来证明所提算法的收敛性。

定理3.1 如果对于正整数m， $R_{i} (k) \neq 0$ 、 $T_{i} (k) \neq 0$ ， $k = 1, 2, \dots, m$ ，那么

$\sum_{i = 1}^{p} Re (t r (R_{i}^{H} (t) T_{i} (s))) = 0, s, t = 1, 2, \dots, m, s < t$ (3.1)

$\sum_{j = 1}^{q} Re (t r (W_{j}^{H} (t) W_{j} (s))) = 0, s, t = 1, 2, \dots, m, s \neq t$ (3.2)

$\sum_{i = 1}^{p} Re (t r (T_{i}^{H} (t) T_{i} (s))) = 0, s, t = 1, 2, \dots, m, s \neq t$ (3.3)

证明：我们采用数学归纳法来证明这个定理，可以得到上述(3.1)~(3.3)。

首先，当 $s < n < m$ ，我们假设有

$\sum_{i = 1}^{p} Re (t r (R_{i}^{H} (n) T_{i} (s))) = 0, s, t = 1, 2, \dots, m, s < t$

$\sum_{j = 1}^{q} Re (t r (W_{j}^{H} (n) W_{j} (s))) = 0, s, t = 1, 2, \dots, m, s \neq t$

$\sum_{i = 1}^{p} Re (t r (T_{i}^{H} (n) T_{i} (s))) = 0, s, t = 1, 2, \dots, m, s \neq t$

根据上述归纳假设，接下来我们来证明 $n + 1$ 时(3.1)~(3.3)的情况，可得

$\begin{array}{l} \sum_{i = 1}^{p} Re (t r (R_{i}^{H} (n + 1) T_{i} (s))) \\ = \sum_{i = 1}^{p} Re (t r ({(R_{i} (n) - α (n) T_{i} (n))}^{H} T_{i} (s))) \\ = \sum_{i = 1}^{p} Re (t r (R_{i}^{H} (n) T_{i} (s))) - α (n) \sum_{i = 1}^{p} Re (t r (T_{i}^{H} (n) T_{i} (s))) \\ = 0 \end{array}$

$\begin{array}{l} \sum_{j = 1}^{q} Re (t r (W_{j}^{H} (n + 1) W_{j} (s))) \\ = \sum_{j = 1}^{q} Re (t r (\frac{1}{2} \sum_{i = 1}^{p} {(A_{i j}^{H} {\tilde{V}}_{i} (n + 1) B_{i j}^{H} + S {(A_{i j}^{H} {\tilde{V}}_{i} (n + 1) B_{i j}^{H})}^{H} S)}^{H} W_{j} (s))) \\ = \frac{1}{\sum_{i = 1}^{p} ‖ V_{i} (n + 1) ‖} \sum_{j = 1}^{q} Re (t r (\frac{1}{2} \sum_{i = 1}^{p} {(A_{i j}^{H} V_{i} (n + 1) B_{i j}^{H} + S {(A_{i j}^{H} V_{i} (n + 1) B_{i j}^{H})}^{H} S)}^{H} W_{j} (s))) \end{array}$

$\begin{array}{l} = \frac{1}{\sum_{i = 1}^{p} ‖ V_{i} (n + 1) ‖} \sum_{j = 1}^{q} Re (t r (\frac{1}{2} (\sum_{i = 1}^{p} B_{i j} (T_{i} (n) - \frac{\sum_{i = 1}^{p} Re (t r (T_{i}^{H} (n) M_{i} (n)))}{τ (n)} {\tilde{V}}_{i} (n) \\ - {\frac{\sum_{j = 1}^{q} Re (t r (W_{j}^{H} (n - 1) N_{j} (n)))}{τ (n - 1)} {\tilde{V}}_{i} (n - 1))}^{H} A_{i j} \\ + S (A_{i j}^{H} (T_{i} (n) - \frac{\sum_{i = 1}^{p} Re (t r (T_{i}^{H} (n) M_{i} (n)))}{τ (n)} {\tilde{V}}_{i} (n) \\ - \frac{\sum_{j = 1}^{q} Re (t r (W_{j}^{H} (n - 1) N_{j} (n)))}{τ (n - 1)} {\tilde{V}}_{i} (n - 1)) B_{i j}^{H}) S) W_{j} (s))) \end{array}$

$\begin{array}{l} = \frac{1}{\sum_{i = 1}^{p} ‖ V_{i} (n + 1) ‖} \sum_{j = 1}^{q} Re (t r (\frac{1}{2} \sum_{i = 1}^{p} (B_{i j} T_{i}^{H} (n) A_{i j} + S A_{i j}^{H} T_{i} (n) B_{i j}^{H} S) W_{j} (s) \begin{matrix} \overset{}{} \end{matrix} \\ - \frac{\sum_{i = 1}^{p} t r (T_{i}^{H} (n) M_{i} (n))}{τ (n)} W_{j}^{H} (n) W_{j} (s) - \frac{\sum_{j = 1}^{q} t r (W_{j}^{H} (n - 1) N_{j} (n))}{τ (n - 1)} W_{j}^{H} (n - 1) W_{j} (s))) \\ = \frac{1}{\sum_{i = 1}^{p} ‖ V_{i} (n + 1) ‖} \sum_{j = 1}^{q} Re (t r (\frac{1}{2} \sum_{i = 1}^{p} (T_{i}^{H} (n) A_{i j} W_{j} (s) B_{i j} + T_{i} (n) {(A_{i j} W_{j} (s) B_{i j})}^{H}) \begin{matrix} \overset{}{} \end{matrix} \\ - \frac{\sum_{i = 1}^{p} Re (t r (T_{i}^{H} (n) M_{i} (n)))}{τ (n)} W_{j}^{H} (n) W_{j} (s) - \frac{\sum_{j = 1}^{q} Re (t r (W_{j}^{H} (n - 1) N_{j} (n)))}{τ (n - 1)} W_{j}^{H} (n - 1) W_{j} (s))) \\ = \frac{1}{\sum_{i = 1}^{p} ‖ V_{i} (n + 1) ‖} \sum_{j = 1}^{q} Re (t r (\sum_{i = 1}^{p} T_{i}^{H} (n) A_{i j} W_{j} (s) B_{i j} - \frac{\sum_{i = 1}^{p} Re (t r (T_{i}^{H} (n) M_{i} (n)))}{τ (n)} W_{j}^{H} (n) W_{j} (s) \\ - \frac{\sum_{j = 1}^{q} Re (t r (W_{j}^{H} (n - 1) N_{j} (n)))}{τ (n - 1)} W_{j}^{H} (n - 1) W_{j} (s))) \end{array}$

$\begin{array}{l} = \frac{1}{\sum_{i = 1}^{p} ‖ V_{i} (n + 1) ‖} (\sum_{j = 1}^{q} Re (t r (\sum_{i = 1}^{p} T_{i}^{H} (n) A_{i j} (U_{j} (s + 1) + \frac{\sum_{i = 1}^{p} Re (t r (T_{i}^{H} (n) M_{i} (s)))}{σ (s)} {\tilde{U}}_{j} (s) \\ + \frac{\sum_{i = 1}^{p} Re (t r (T_{i}^{H} (s - 1) M_{i} (s)))}{σ (s - 1)} {\tilde{U}}_{j} (s - 1)) B_{i j})) \\ - \frac{\sum_{j = 1}^{q} Re (t r (W_{j}^{H} (n - 1) N_{j} (n)))}{τ (n - 1)} Re (t r (\sum_{j = 1}^{q} W_{j}^{H} (n - 1) W_{j} (s)))) \end{array}$

$\begin{array}{l} = \frac{1}{\sum_{i = 1}^{p} ‖ V_{i} (n + 1) ‖} (\sum_{j = 1}^{q} ‖ U_{j} (s + 1) ‖ \sum_{i = 1}^{p} Re (t r (T_{i}^{H} (n) T_{i} (s + 1))) \begin{matrix} \overset{}{} \end{matrix} \\ + \frac{\sum_{i = 1}^{p} Re (t r (T_{i}^{H} (s) M_{i} (s)))}{σ (s)} \sum_{i = 1}^{p} Re (t r (T_{i}^{H} (n) T_{i} (s))) \\ + \frac{\sum_{i = 1}^{p} Re (t r (T_{i}^{H} (s - 1) M_{i} (s)))}{σ (s - 1)} \sum_{i = 1}^{p} Re (t r (T_{i}^{H} (n) T_{i} (s - 1))) \\ - \frac{\sum_{j = 1}^{q} t r (W_{j}^{H} (n - 1) N_{j} (n))}{τ (n - 1)} t r (\sum_{j = 1}^{q} W_{j}^{H} (n - 1) W_{j} (s))) \end{array}$

$\begin{array}{l} = \frac{\sum_{j = 1}^{q} ‖ U_{j} (s + 1) ‖}{\sum_{i = 1}^{p} ‖ V_{i} (n + 1) ‖} \sum_{i = 1}^{p} Re (t r (T_{i}^{H} (n) T_{i} (s + 1))) \\ - \frac{\sum_{j = 1}^{q} Re (t r (W_{j}^{H} (n - 1) W_{j} (s)))}{\sum_{i = 1}^{p} ‖ V_{i} (n + 1) ‖} \frac{\sum_{j = 1}^{q} Re (t r (W_{j}^{H} (n - 1) N_{j} (n)))}{τ (n - 1)} \end{array}$ (3.4)

$\begin{array}{l} \sum_{i = 1}^{p} Re (t r (T_{i}^{H} (n + 1) T_{i} (s))) \\ = \sum_{i = 1}^{p} Re (t r ({(\sum_{j = 1}^{q} A_{i j} {\tilde{U}}_{j} (n + 1) B_{i j})}^{H} T_{i} (s))) \\ = \frac{1}{\sum_{j = 1}^{q} ‖ U_{j} (n + 1) ‖} \sum_{i = 1}^{p} Re (t r ({(\sum_{j = 1}^{q} A_{i j} U_{j} (n + 1) B_{i j})}^{H} T_{i} (s))) \end{array}$

$\begin{array}{l} = \frac{1}{\sum_{j = 1}^{q} ‖ U_{j} (n + 1) ‖} \sum_{j = 1}^{q} Re (t r ((A_{i j} (W_{j} (n) - \frac{\sum_{i = 1}^{p} Re (t r (T_{i}^{H} (n) M_{i} (n)))}{σ (n)} {\tilde{U}}_{j} (n) \\ - {\frac{\sum_{i = 1}^{p} Re (t r (T_{i}^{H} (n - 1) M_{i} (n)))}{σ (n - 1)} {\tilde{U}}_{j} (n - 1)) B_{i j})}^{H} T_{i} (s))) \\ = \frac{1}{\sum_{j = 1}^{q} ‖ U_{j} (n + 1) ‖} \sum_{j = 1}^{q} Re (t r ((A_{i j} W_{j} (n) B_{i j} - \frac{\sum_{i = 1}^{p} Re (t r (T_{i}^{H} (n) M_{i} (n)))}{σ (n)} T_{i} (n) \\ - {\frac{\sum_{i = 1}^{p} Re (t r (T_{i}^{H} (n - 1) M_{i} (n)))}{σ (n - 1)} T_{i} (n - 1))}^{H} T_{i} (s))) \\ = \frac{1}{\sum_{j = 1}^{q} ‖ U_{j} (n + 1) ‖} (\sum_{i = 1}^{p} Re (t r (\sum_{j = 1}^{q} B_{i j}^{H} W_{j}^{H} (n) A_{i j}^{H} T_{i} (s))) \begin{matrix} \end{matrix} \\ - \frac{\sum_{i = 1}^{p} Re (t r (T_{i}^{H} (n) M_{i} (n)))}{σ (n)} \sum_{i = 1}^{p} Re (t r (T_{i}^{H} (n) T_{i} (s))) \\ - \frac{\sum_{i = 1}^{p} Re (t r (T_{i}^{H} (n - 1) M_{i} (n)))}{σ (n - 1)} \sum_{i = 1}^{p} Re (t r (T_{i}^{H} (n - 1) T_{i} (s)))) \end{array}$

$\begin{array}{l} = \frac{1}{\sum_{j = 1}^{q} ‖ U_{j} (n + 1) ‖} (\sum_{i = 1}^{p} \sum_{j = 1}^{q} Re (t r (W_{j}^{H} (n) (A_{i j}^{H} T_{i} (s) B_{i j}^{H}))) \begin{matrix} \overset{}{} \end{matrix} \\ - \frac{\sum_{i = 1}^{p} Re (t r (T_{i}^{H} (n - 1) M_{i} (n)))}{σ (n - 1)} \sum_{i = 1}^{p} Re (t r (T_{i}^{H} (n - 1) T_{i} (s)))) \\ = \frac{1}{\sum_{j = 1}^{q} ‖ U_{j} (n + 1) ‖} (\frac{1}{2} \sum_{i = 1}^{p} \sum_{j = 1}^{q} Re (t r (W_{j}^{H} (n) (A_{i j}^{H} T_{i} (s) B_{i j}^{H} + S {(A_{i j}^{H} T_{i} (s) B_{i j}^{H})}^{H} S))) \begin{matrix} \overset{}{} \end{matrix} \\ - \frac{\sum_{i = 1}^{p} Re (t r (T_{i}^{H} (n - 1) M_{i} (n)))}{σ (n - 1)} \sum_{i = 1}^{p} Re (t r (T_{i}^{H} (n - 1) T_{i} (s)))) \end{array}$

$\begin{array}{l} = \frac{1}{\sum_{j = 1}^{q} ‖ U_{j} (n + 1) ‖} (\frac{1}{2} \sum_{i = 1}^{p} \sum_{j = 1}^{q} Re (t r (W_{j}^{H} (n) (A_{i j}^{H} (V_{i} (s + 1) + \frac{\sum_{i = 1}^{p} Re (t r (T_{i}^{H} (s) M_{i} (s)))}{τ (s)} {\tilde{V}}_{i} (s) \\ + \frac{\sum_{j = 1}^{q} Re (t r (W_{j}^{H} (s - 1) N_{j} (s)))}{τ (s - 1)} {\tilde{V}}_{i} (s - 1)) B_{i j}^{H} + S (A_{i j}^{H} (V_{i} (s + 1) + \frac{\sum_{i = 1}^{p} Re (t r (T_{i}^{H} (s) M_{i} (s)))}{τ (s)} {\tilde{V}}_{i} (s) \\ + {\frac{\sum_{j = 1}^{q} Re (t r (W_{j}^{H} (s - 1) N_{j} (s)))}{τ (s - 1)} {\tilde{V}}_{i} (s - 1)) B_{i j}^{H})}^{H} S))) \\ - \frac{\sum_{i = 1}^{p} Re (t r (T_{i}^{H} (n - 1) M_{i} (n)))}{σ (n - 1)} \sum_{i = 1}^{p} Re (t r (T_{i}^{H} (n - 1) T_{i} (s)))) \end{array}$

$\begin{array}{l} = \frac{1}{\sum_{j = 1}^{q} ‖ U_{j} (n + 1) ‖} (\sum_{j = 1}^{q} Re (t r (W_{j}^{H} (n) (W_{j} (s + 1) \sum_{i = 1}^{p} ‖ V_{i} (s + 1) ‖ \begin{matrix} \overset{}{} \end{matrix} \\ + \frac{\sum_{i = 1}^{p} Re (t r (T_{i}^{H} (s) M_{i} (s)))}{τ (s)} W_{j} (s) + \frac{\sum_{j = 1}^{q} Re (t r (W_{j}^{H} (s - 1) N_{j} (s)))}{τ (s - 1)} W_{j} (s - 1)))) \\ - \frac{\sum_{i = 1}^{p} Re (t r (T_{i}^{H} (n - 1) M_{i} (n)))}{σ (n - 1)} \sum_{i = 1}^{p} Re (t r (T_{i}^{H} (n - 1) T_{i} (s)))) \\ = \frac{\sum_{i = 1}^{p} ‖ V_{i} (s + 1) ‖}{\sum_{j = 1}^{q} ‖ U_{j} (n + 1) ‖} \sum_{j = 1}^{q} Re (t r (W_{j}^{H} (n) W_{j} (s + 1))) \\ - \frac{\sum_{i = 1}^{p} Re (t r (T_{i}^{H} (n - 1) M_{i} (n)))}{\sum_{j = 1}^{q} ‖ U_{j} (n + 1) ‖} \frac{\sum_{i = 1}^{p} Re (t r (T_{i}^{H} (n - 1) T_{i} (s)))}{σ (n - 1)} \end{array}$ (3.5)

当 $s = n - 1$ ，由于 $s < n$ ，根据上述(3.1)~(3.3)，可得

$\sum_{i = 1}^{p} Re (t r (R_{i}^{H} (n + 1) T_{i} (n - 1))) = 0.$

$\begin{array}{l} \sum_{j = 1}^{q} Re (t r (W_{j}^{H} (n + 1) W_{j} (n - 1))) \\ = \frac{\sum_{j = 1}^{q} ‖ U_{j} (n) ‖}{\sum_{i = 1}^{p} ‖ V_{i} (n + 1) ‖} \sum_{i = 1}^{p} Re (t r (T_{i}^{H} (n) T_{i} (n))) \\ - \frac{\sum_{j = 1}^{q} Re (t r (W_{j}^{H} (n - 1) W_{j} (n - 1)))}{\sum_{i = 1}^{p} ‖ V_{i} (n + 1) ‖} \frac{\sum_{j = 1}^{q} Re (t r (W_{j}^{H} (n - 1) N_{j} (n)))}{τ (n - 1)} \end{array}$

$\begin{array}{l} = \frac{\sum_{j = 1}^{q} ‖ U_{j} (n) ‖}{\sum_{i = 1}^{p} ‖ V_{i} (n + 1) ‖} \sum_{i = 1}^{p} Re (t r (T_{i}^{H} (n) T_{i} (n))) - \frac{\sum_{j = 1}^{q} Re (t r (W_{j}^{H} (n - 1) N_{j} (n)))}{\sum_{i = 1}^{p} ‖ V_{i} (n + 1) ‖} \\ = \frac{\sum_{j = 1}^{q} ‖ U_{j} (n) ‖}{\sum_{i = 1}^{p} ‖ V_{i} (n + 1) ‖} \sum_{i = 1}^{p} Re (t r (T_{i}^{H} (n) T_{i} (n))) - \frac{\sum_{j = 1}^{q} Re (t r (W_{j}^{H} (n - 1) \sum_{i = 1}^{p} A_{i j}^{H} T_{i} (n) B_{i j}^{H}))}{\sum_{i = 1}^{p} ‖ V_{i} (n + 1) ‖} \\ = \frac{\sum_{j = 1}^{q} ‖ U_{j} (n) ‖}{\sum_{i = 1}^{p} ‖ V_{i} (n + 1) ‖} \sum_{i = 1}^{p} Re (t r (T_{i}^{H} (n) T_{i} (n))) - \frac{\sum_{j = 1}^{q} \sum_{i = 1}^{p} Re (t r ({(A_{i j} W_{j} (n - 1) B_{i j})}^{H} T_{i} (n)))}{\sum_{i = 1}^{p} ‖ V_{i} (n + 1) ‖} \end{array}$

$\begin{array}{l} = \frac{\sum_{j = 1}^{q} ‖ U_{j} (n) ‖}{\sum_{i = 1}^{p} ‖ V_{i} (n + 1) ‖} \sum_{i = 1}^{p} Re (t r (T_{i}^{H} (n) T_{i} (n))) - \frac{1}{\sum_{i = 1}^{p} ‖ V_{i} (n + 1) ‖} \sum_{i = 1}^{p} Re (t r ((\sum_{j = 1}^{q} ‖ U_{j} (n) ‖ T_{i} (n) \begin{matrix} \overset{}{} \end{matrix} \\ + \frac{\sum_{i = 1}^{p} Re (t r (T_{i}^{H} (n - 1) M_{i} (n - 1)))}{σ (n - 1)} T_{i} (n - 1) \\ + {\frac{\sum_{i = 1}^{p} Re (t r (T_{i}^{H} (n - 2) M_{i} (n - 1)))}{σ (n - 2)} T_{i} (n - 2))}^{H} T_{i} (n))) \\ = \frac{\sum_{j = 1}^{q} ‖ U_{j} (n) ‖}{\sum_{i = 1}^{p} ‖ V_{i} (n + 1) ‖} \sum_{i = 1}^{p} Re (t r (T_{i}^{H} (n) T_{i} (n))) - \frac{\sum_{j = 1}^{q} ‖ U_{j} (n) ‖}{\sum_{i = 1}^{p} ‖ V_{i} (n + 1) ‖} \sum_{i = 1}^{p} Re (t r (T_{i}^{H} (n) T_{i} (n))) \\ = 0. \end{array}$

$\begin{array}{l} \sum_{i = 1}^{p} Re (t r (T_{i}^{H} (n + 1) T_{i} (n - 1))) \\ = \frac{\sum_{i = 1}^{p} ‖ V_{i} (n) ‖}{\sum_{j = 1}^{q} ‖ U_{j} (n + 1) ‖} \sum_{j = 1}^{q} Re (t r (W_{j}^{H} (n) W_{j} (n))) \\ - \frac{\sum_{i = 1}^{p} Re (t r (T_{i}^{H} (n - 1) M_{i} (n)))}{\sum_{j = 1}^{q} ‖ U_{j} (n + 1) ‖} \frac{\sum_{i = 1}^{p} Re (t r (T_{i}^{H} (n - 1) T_{i} (n - 1)))}{σ (n - 1)} \\ = \frac{\sum_{i = 1}^{p} ‖ V_{i} (n) ‖}{\sum_{j = 1}^{q} ‖ U_{j} (n + 1) ‖} \sum_{j = 1}^{q} Re (t r (W_{j}^{H} (n) W_{j} (n))) - \frac{\sum_{i = 1}^{p} Re (t r (T_{i}^{H} (n - 1) M_{i} (n)))}{\sum_{j = 1}^{q} ‖ U_{j} (n + 1) ‖} \\ = \frac{\sum_{i = 1}^{p} ‖ V_{i} (n) ‖}{\sum_{j = 1}^{q} ‖ U_{j} (n + 1) ‖} \sum_{j = 1}^{q} Re (t r (W_{j}^{H} (n) W_{j} (n))) - \frac{\sum_{i = 1}^{p} Re (t r (T_{i}^{H} (n - 1) (\sum_{j = 1}^{q} A_{i j} W_{j} (n) B_{i j})))}{\sum_{j = 1}^{q} ‖ U_{j} (n + 1) ‖} \end{array}$

$\begin{array}{l} = \frac{\sum_{i = 1}^{p} ‖ V_{i} (n) ‖}{\sum_{j = 1}^{q} ‖ U_{j} (n + 1) ‖} \sum_{j = 1}^{q} Re (t r (W_{j}^{H} (n) W_{j} (n))) \\ - \frac{1}{\sum_{j = 1}^{q} ‖ U_{j} (n + 1) ‖} \sum_{i = 1}^{p} \sum_{j = 1}^{q} Re (t r ((A_{i j}^{H} T_{i} (n - 1) B_{i j}^{H}) W_{j} (n))) \\ = \frac{\sum_{i = 1}^{p} ‖ V_{i} (n) ‖}{\sum_{j = 1}^{q} ‖ U_{j} (n + 1) ‖} \sum_{j = 1}^{q} Re (t r (W_{j}^{H} (n) W_{j} (n))) \\ - \frac{1}{\sum_{j = 1}^{q} ‖ U_{j} (n + 1) ‖} \sum_{j = 1}^{q} Re (t r (\frac{1}{2} \sum_{i = 1}^{p} {(A_{i j}^{H} T_{i} (n - 1) B_{i j}^{H} + S {(A_{i j}^{H} T_{i} (n - 1) B_{i j}^{H})}^{H} S)}^{H} W_{j} (n))) \\ = \frac{\sum_{i = 1}^{p} ‖ V_{i} (n) ‖}{\sum_{j = 1}^{q} ‖ U_{j} (n + 1) ‖} \sum_{j = 1}^{q} Re (t r (W_{j}^{H} (n) W_{j} (n))) \\ - \frac{1}{\sum_{j = 1}^{q} ‖ U_{j} (n + 1) ‖} \sum_{j = 1}^{q} Re (t r ((\sum_{i = 1}^{p} ‖ V_{i} (n) ‖ W_{j} (n) + \frac{Re \sum_{i = 1}^{p} t r (T_{i}^{H} (n - 1) M_{i} (n - 1))}{τ (n - 1)} W_{j} (n - 1) \\ + {\frac{Re \sum_{j = 1}^{q} t r (W_{j}^{H} (n - 2) N_{j} (n - 1))}{τ (n - 2)} W_{j} (n - 2))}^{H} W_{j} (n))) \end{array}$

$\begin{array}{l} = \frac{\sum_{i = 1}^{p} ‖ V_{i} (n) ‖}{\sum_{j = 1}^{q} ‖ U_{j} (n + 1) ‖} \sum_{j = 1}^{q} Re (t r (W_{j}^{H} (n) W_{j} (n))) - \frac{\sum_{i = 1}^{p} ‖ V_{i} (n) ‖}{\sum_{j = 1}^{q} ‖ U_{j} (n + 1) ‖} \sum_{j = 1}^{q} Re (t r (W_{j}^{H} (n) W_{j} (n))) \\ = 0. \end{array}$

当 $s = n$ 时，通过归纳假设可得

$\begin{array}{l} \sum_{i = 1}^{p} Re (t r (R_{i}^{H} (n + 1) T_{i} (n))) \\ = \sum_{i = 1}^{p} Re (t r ({(R_{i} (n) - α (n) T_{i} (n))}^{H} T_{i} (n))) \\ = \sum_{i = 1}^{p} Re (t r (R_{i}^{H} (n) T_{i} (n))) - \frac{\sum_{i = 1}^{p} Re (t r (T_{i}^{H} (n) R_{i} (n)))}{\sum_{i = 1}^{p} {‖ T_{i} (n) ‖}^{2}} \sum_{i = 1}^{p} Re (t r (T_{i}^{H} (n) T_{i} (n))) \\ = \sum_{i = 1}^{p} Re (t r (R_{i}^{H} (n) T_{i} (n))) - \sum_{i = 1}^{p} Re (t r (T_{i}^{H} (n) R_{i} (n))) \\ = 0. \end{array}$

$\begin{array}{l} \sum_{j = 1}^{q} Re (t r (W_{j}^{H} (n + 1) W_{j} (n))) \\ = \frac{1}{\sum_{i = 1}^{p} ‖ V_{i} (n + 1) ‖} \sum_{j = 1}^{q} Re (t r ((\frac{1}{2} \sum_{i = 1}^{p} (A_{i j}^{H} T_{i} (n) B_{i j}^{H} + S {(A_{i j}^{H} T_{i} (n) B_{i j}^{H})}^{H} S) \begin{matrix} \overset{}{} \end{matrix} \\ - \frac{\sum_{i = 1}^{p} Re (t r (T_{i}^{H} (n) M_{i} (n)))}{τ (n)} W_{j} (n) - \frac{\sum_{j = 1}^{q} Re (t r (W_{j}^{H} (n - 1) N_{j} (n)))}{τ (n - 1)} W_{j} (n - 1)) W_{j} (n))) \\ = \frac{1}{\sum_{i = 1}^{p} ‖ V_{i} (n + 1) ‖} (\sum_{i = 1}^{p} Re (t r (T_{i}^{H} (n) \sum_{j = 1}^{q} A_{i j} W_{j} (n) B_{i j})) - \frac{\sum_{i = 1}^{p} Re (t r (T_{i}^{H} (n) M_{i} (n)))}{τ (n)} \sum_{j = 1}^{q} Re (t r (W_{j}^{H} (n) W_{j} (n)))) \end{array}$

$\begin{array}{l} = \frac{1}{\sum_{i = 1}^{p} ‖ V_{i} (n + 1) ‖} (\sum_{i = 1}^{p} Re (t r (T_{i}^{H} (n) M_{i} (n))) - \frac{\sum_{i = 1}^{p} Re (t r (T_{i}^{H} (n) M_{i} (n)))}{\sum_{j = 1}^{q} {‖ W_{j} (n) ‖}^{2}} \sum_{j = 1}^{q} Re (t r (W_{j}^{H} (n) W_{j} (n)))) \\ = \frac{1}{\sum_{i = 1}^{p} ‖ V_{i} (n + 1) ‖} (\sum_{i = 1}^{p} Re (t r (T_{i}^{H} (n) M_{i} (n))) - \sum_{i = 1}^{p} Re (t r (T_{i}^{H} (n) M_{i} (n)))) \\ = 0. \end{array}$

$\begin{array}{l} \sum_{i = 1}^{p} Re (t r (T_{i}^{H} (n + 1) T_{i} (n))) \\ = \frac{1}{\sum_{j = 1}^{q} ‖ U_{j} (n + 1) ‖} \sum_{i = 1}^{p} Re (t r ((\sum_{j}^{q} A_{i j} W_{j} (n) B_{i j} - \frac{\sum_{i = 1}^{p} Re (t r (T_{i}^{H} (n) M_{i} (n)))}{σ (n)} T_{i} (n) \\ - {\frac{\sum_{i = 1}^{p} Re (t r (T_{i}^{H} (n - 1) M_{i} (k)))}{σ (n - 1)} T_{i} (n - 1))}^{H} T_{i} (n))) \end{array}$

$\begin{array}{l} = \frac{1}{\sum_{j = 1}^{q} ‖ U_{j} (n + 1) ‖} (\sum_{i = 1}^{p} Re (t r (M_{i}^{H} (n) T_{i} (n))) - \frac{\sum_{i = 1}^{p} Re (t r (T_{i}^{H} (n) M_{i} (n)))}{\sum_{i = 1}^{p} {‖ T_{i} (n) ‖}^{2}} \sum_{i = 1}^{p} Re (t r (T_{i}^{H} (n) T_{i} (n)))) \\ = \frac{1}{\sum_{j = 1}^{q} ‖ U_{j} (n + 1) ‖} (\sum_{i = 1}^{p} Re (t r (M_{i}^{H} (n) T_{i} (n))) - \sum_{i = 1}^{p} Re (t r (M_{i}^{H} (n) T_{i} (n)))) \\ = 0. \end{array}$

因此，对于次数 $n + 1$ 成立，数学归纳法证明完成。 □

定理3.2假设矩阵方程组(1.1)是相容的，在没有舍入误差的情况下，对任意初始矩阵 $X_{j} (1) \in ℙ ℂ^{n \times n}$ ，根据算法3.1，可以在有限步迭代得到矩阵方程组(1.1)的perhermitian解。

证明首先，定义空间 $ℂ^{m \times l} \times ℂ^{m \times l} \times \dots \times ℂ^{m \times l}$ 的实内积为 $〈 T_{i}, T_{j} 〉 = Re (t r (T_{j}^{H} T_{i}))$ ，其中 $T_{i}, T_{j} \in ℂ^{m \times l}, i, j = 1, 2, \dots, p$ 。如果 $T_{i} (k) \neq 0, k = 1, 2, \dots, p m l$ ，那么 ${T_{1} (k), T_{2} (k), \dots, T_{p} (k)}$ 是该空间的一组正交基。根据(3.1)式可以得到 $R_{i} (p m l + 1) = 0$ ，即 $X_{j} (p m l + 1), j = 1, 2, \dots, q$ 是矩阵方程(1.1)的perhermitian解。

定理3.3 算法3.1中残量范数具有以下性质

$\sum_{i = 1}^{p} {‖ R_{i} (k + 1) ‖}^{2} \leq \sum_{i = 1}^{p} {‖ R_{i} (k) ‖}^{2} .$

证明：

$\begin{matrix} \sum_{i = 1}^{p} {‖ R_{i} (k + 1) ‖}^{2} = \sum_{i = 1}^{p} Re (t r (R_{i}^{H} (k + 1) R_{i} (k + 1))) \\ = \sum_{i = 1}^{p} Re (t r ({(R_{i} (k) - α (k) T_{i} (k))}^{H} (R_{i} (k) - α (k) T_{i} (k)))) \\ = \sum_{i = 1}^{p} Re (t r ((R_{i}^{H} (k) - α (k) T_{i}^{H} (k)) (R_{i} (k) - α (k) T_{i} (k)))) \\ = \sum_{i = 1}^{p} Re (t r (R_{i}^{H} (k) R_{i} (k))) + α^{2} (k) \sum_{i = 1}^{p} Re (t r (T_{i}^{H} (k) T_{i} (k))) \\ - 2 α (k) \sum_{i = 1}^{p} Re (t r (R_{i}^{H} (k) T_{i} (k))) \end{matrix}$

$\begin{matrix} = \sum_{i = 1}^{p} {‖ R_{i} (k) ‖}^{2} + α^{2} (k) σ (k) - 2 α^{2} (k) σ (k) \\ = \sum_{i = 1}^{p} {‖ R_{i} (k) ‖}^{2} - α^{2} (k) σ (k) \leq \sum_{i = 1}^{p} {‖ R_{i} (k) ‖}^{2} . \end{matrix}$

□

定理3.3表明，如果 $\sum_{i = 1}^{p} {‖ R_{i} (k) ‖}^{2} \neq 0$ 且 $\sum_{i = 1}^{p} Re (t r (R_{i}^{H} (k) T_{i} (k))) \neq 0$ ，那么 $\sum_{i = 1}^{p} {‖ R_{i} (k) ‖}^{2}$ 是严格单调递减的，所以算法3.1是收敛的。

3.3. 最小范数Perhermitian解

接下来考虑Sylvester矩阵方程组(1.1)的最佳逼近perhermitian解，即最小范数perhermitian解。

引理3.1 [19] [24] [25] [26] 设线性矩阵方程 $A x = b$ 有解 $x^{*} \in R (A^{T})$ ，其中 $R (A^{T})$ 表示 $A^{T}$ 的列空间，则 $x^{*}$ 是 $A x = b$ 的唯一最小范数解。

定理3.4 设矩阵方程组(1.1)是相容的，初始值取 $X_{j} (1) = \sum_{i = 1}^{p} (A_{i j}^{H} E_{i} B_{i j}^{H} + S {(A_{i j}^{H} E_{i} B_{i j}^{H})}^{H} S)$ ，

$Z_{j} (1) = \sum_{i = 1}^{p} (A_{i j}^{H} F_{i} B_{i j}^{H} + S {(A_{i j}^{H} F_{i} B_{i j}^{H})}^{H} S)$ ， $j = 1, 2, \dots, q$ ，其中 $E_{i}$ 和 $F_{i}$ 为任意的 $ℂ^{m \times l}$ 矩阵，特别地，取

$X_{j} (1) = 0$ ， $Z_{j} (1) = 0$ ，S是适当维数的反射矩阵。如果矩阵方程组(1.1)有perhermitian解，那么算法3.1经过有限步迭代求出的解是矩阵方程(1.1)的唯一的最小范数perhermitian解 $X_{j}^{*}$ ， $j = 1, 2, \dots, q$ 。

证明：根据Kronecker积，将 $X_{j} (1) = \sum_{i = 1}^{p} (A_{i j}^{H} E_{i} B_{i j}^{H} + S {(A_{i j}^{H} E_{i} B_{i j}^{H})}^{H} S)$ 改写为

$\underset{X^{*} (1)}{\underset{︸}{(\begin{matrix} {(v e c (X_{1} (1)))}^{H} \\ ⋮ \\ {(v e c (X_{q} (1)))}^{H} \end{matrix})}} = \underset{A^{H}}{\underset{︸}{(\begin{matrix} B_{11} \otimes A_{11}^{H} & S A_{11}^{H} \otimes S B_{11} & \dots & B_{p 1} \otimes A_{p 1}^{H} & S A_{p 1}^{H} \otimes S B_{p 1} \\ ⋮ & ⋮ & ⋱ & ⋮ & ⋮ \\ B_{1 q} \otimes A_{1 q}^{H} & S A_{1 q}^{H} \otimes S B_{1 q} & \dots & B_{p q} \otimes A_{p q}^{H} & S A_{p q}^{H} \otimes S B_{p q} \end{matrix})}} \underset{M}{\underset{︸}{(\begin{matrix} {(v e c (E_{1}))}^{H} \\ {(v e c (E_{1}^{H}))}^{H} \\ ⋮ \\ {(v e c (E_{p}))}^{H} \\ {(v e c (E_{p}^{H}))}^{H} \end{matrix})}}$

因此，如果通过上述选择 $X_{j} (1)$ ，那么通过算法3.1得到的 $X_{j} (k)$ 满足

$X^{*} (k) = {({(v e c (X_{1} (k)))}^{H}, \dots, {(v e c (X_{q} (k)))}^{H})}^{H} \in R (A^{H})$ ，其中 $R (A^{H})$ 表示 $A^{H}$ 的列空间。由引理3.1可知，如果 $X_{j} (1) = \sum_{i = 1}^{p} (A_{i j}^{H} E_{i} B_{i j}^{H} + S {(A_{i j}^{H} E_{i} B_{i j}^{H})}^{H} S)$ ， $Z_{j} (1) = \sum_{i = 1}^{p} (A_{i j}^{H} F_{i} B_{i j}^{H} + S {(A_{i j}^{H} F_{i} B_{i j}^{H})}^{H} S)$ ，作为初始解，

特别是 $X_{j} (1) = 0$ ， $Z_{j} (1) = 0$ ，那么可以通过算法3.1来求解矩阵方程组(1.1)的唯一最小范数perhermitian解。

□

4. 数值算例

在这个部分，我们给出两个算例来说明所提出的算法的有效性。当 $r (k) = \sqrt{\sum_{i = 1}^{p} {‖ R_{i} (k) ‖}^{2}} \leq 10^{- 10}$ 时，停止迭代，并且 $X_{j} (k)$ 被视为矩阵方程组(1.1)的唯一最小范数perhermitian解。

例4.1 给定Sylvester矩阵方程为

$A_{11} X_{1} B_{11} + A_{12} X_{2} B_{12} = C_{1},$

其中

$A_{11} = (\begin{matrix} 6 + 5 i & 5 + 6 i & 1 + 6 i \\ 3 + 7 i & 10 + 4 i & 2 + i \\ 2 + i & 9 + 10 i & 3 + 2 i \\ 3 + 9 i & 4 + 6 i & 6 + 3 i \end{matrix}), B_{11} = (\begin{matrix} 8 + 5 i & 9 + 2 i & 9 + 9 i & 1 + 3 i \\ 6 + 3 i & 7 + i & 2 + 4 i & 6 + 4 i \\ 2 + 7 i & 4 + 3 i & 1 + 10 i & 4 + 7 i \end{matrix}),$

$A_{12} = (\begin{matrix} 4 + 3 i & 10 + 2 i & 4 + i \\ 2 + 5 i & 1 + 5 i & 8 + 7 i \\ 3 + 7 i & 4 + i & 2 + 10 i \\ 10 + 2 i & 6 + 8 i & 10 + 4 i \end{matrix}), B_{12} = (\begin{matrix} 6 + 2 i & 9 + 4 i & 8 + 3 i & 6 + 4 i \\ 10 + 8 i & 9 + 9 i & 5 + 3 i & 8 + 9 i \\ 10 + 2 i & 2 + 3 i & 6 + 9 i & 1 + i \end{matrix}),$

$C_{1} = 10^{2} \times (\begin{matrix} 1.3500 + 2.8400 i & 1.6000 + 2.9600 i & 0.1800 + 2.6500 i & 0.3600 + 2.5500 i \\ 0.7200 + 3.1900 i & 0.4100 + 2.2600 i & - 0.6400 + 3.4700 i & - 0.1700 + 2.0000 i \\ 0.6300 + 3.2400 i & 0.7500 + 2.5500 i & - 0.8800 + 2.7500 i & 0.1600 + 2.4200 i \\ 1.2000 + 4.0300 i & 1.1800 + 3.8500 i & 0.1000 + 4.1700 i & 0.1300 + 3.0800 i \end{matrix}),$

求其唯一最小范数perhermitian解。

选取初始矩阵

$X_{1} (1) = 10^{3} \times (\begin{matrix} 0.5979 + 0.0000 i & 0.9305 + 0.2703 i & 0.2987 - 0.2502 i \\ 0.9305 - 0.2703 i & 1.0413 + 0.0000 i & 0.4424 - 0.5889 i \\ 0.2987 + 0.2502 i & 0.4424 + 0.5889 i & 0.1692 + 0.0000 i \end{matrix}),$

$X_{1} (2) = 10^{3} \times (\begin{matrix} 0.8504 + 0.0000 i & 0.9667 - 0.3004 i & 0.7801 + 0.0635 i \\ 0.9667 + 0.3004 i & 1.1728 + 0.0000 i & 0.9089 + 0.4224 i \\ 0.7801 - 0.0635 i & 0.9089 - 0.4224 i & 0.5345 + 0.0000 i \end{matrix}),$

根据算法3.1，经过24步迭代终止，得到该矩阵方程的唯一最小范数perhermitian解：

$X_{1} (24) = 10^{3} \times (\begin{matrix} 1.1948 + 0.0000 i & 1.8609 + 0.5406 i & 0.5974 - 0.5004 i \\ 1.8609 - 0.5406 i & 2.0817 + 0.0000 i & 0.8847 - 1.1779 i \\ 0.5974 + 0.5004 i & 0.8847 + 1.1779 i & 0.3373 + 0.0000 i \end{matrix}),$

$X_{2} (24) = 10^{3} \times (\begin{matrix} 1.6998 + 0.0000 i & 1.9334 - 0.6008 i & 1.5601 + 0.1270 i \\ 1.9334 + 0.6008 i & 2.3446 + 0.0000 i & 1.8178 + 0.8648 i \\ 1.5601 - 0.1270 i & 1.8178 - 0.8648 i & 1.0680 + 0.0000 i \end{matrix}),$

并且，相应残差的范数 $r = 2.4009 \times 10^{- 13} < 10^{- 10}$ 。

例4.2 给定Sylvester矩阵方程组为

${\begin{cases} A_{11} X_{1} B_{11} + A_{12} X_{2} B_{12} = C_{1} \\ A_{21} X_{1} B_{21} + A_{22} X_{2} B_{22} = C_{2} \end{cases}$ ，

其中

$A_{11} = (\begin{matrix} 10 + 2 i & 9 + 6 i & 1 + 8 i \\ 8 + 4 i & 5 + 4 i & 4 + i \\ 10 + 6 i & 9 + i & 9 + 7 i \\ 6 + 10 i & 6 + 8 i & 5 + 3 i \end{matrix}), B_{11} = (\begin{matrix} 4 + i & 9 + 8 i & 4 + 6 i & 4 + 3 i \\ 6 + 9 i & 6 + 5 i & 7 + 5 i & 6 + 3 i \\ 5 + 2 i & 6 + 10 i & 6 + 5 i & 3 + 4 i \end{matrix}),$

$A_{12} = (\begin{matrix} 9 + 9 i & 4 + 3 i & 8 + 9 i \\ 3 + 10 i & 4 + 4 i & 8 + 4 i \\ 10 + 3 i & 8 + 6 i & 3 + 7 i \\ 4 + 5 i & 7 + 4 i & 9 + 7 i \end{matrix}), B_{12} = (\begin{matrix} 5 + 6 i & 5 + 6 i & 5 + 6 i & 10 + 3 i \\ 8 + 4 i & 10 + 3 i & 1 + 10 i & 1 + 9 i \\ 1 + 2 i & 10 + 2 i & 2 + 6 i & 1 + 3 i \end{matrix}),$

$A_{21} = (\begin{matrix} 2 + 5 i & 9 + 5 i & 2 + i \\ 10 + 8 i & 2 + i & 7 + 10 i \\ 3 + 4 i & 10 + 8 i & 4 + 7 i \\ 2 + 9 i & 6 + 5 i & 4 + 9 i \end{matrix}), B_{21} = (\begin{matrix} 3 + 3 i & 5 + 3 i & 10 + 6 i & 5 + 7 i \\ 6 + 4 i & 8 + 4 i & 10 + 5 i & 3 + 10 i \\ 8 + 9 i & 7 + 2 i & 6 + 10 i & 4 + 4 i \end{matrix}),$

$A_{22} = (\begin{matrix} 5 + 7 i & 4 + 9 i & 4 + 3 i \\ 7 + 5 i & 3 + 4 i & 10 + i \\ 2 + 6 i & 4 + 3 i & 2 + 9 i \\ 8 + 9 i & 7 + 3 i & 5 + 10 i \end{matrix}), B_{22} = (\begin{matrix} 5 + 5 i & 4 + 4 i & 3 + 7 i & 10 + 2 i \\ 4 + 2 i & 5 + i & 1 + 2 i & 1 + 10 i \\ 5 + 9 i & 4 + 10 i & 1 + 9 i & 2 + i \end{matrix}),$

$C_{1} = 10^{2} \times (\begin{matrix} 0.2800 + 3.4100 i & 1.0800 + 4.8400 i & - 0.4600 + 4.1600 i & 0.6200 + 3.1800 i \\ 0.1100 + 2.4200 i & 1.1900 + 3.7100 i & - 0.4700 + 3.1100 i & 0.1000 + 2.7500 i \\ 1.7100 + 3.4200 i & 1.8500 + 5.5200 i & 0.2500 + 4.1600 i & 0.9900 + 2.9800 i \\ 0.2200 + 3.0700 i & 0.9400 + 4.8200 i & - 0.8600 + 3.9600 i & - 0.0700 + 3.1600 i \end{matrix}),$

$C_{2} = 10^{2} \times (\begin{matrix} 0.1300 + 2.6800 i & 0.4800 + 2.6700 i & - 0.1400 + 2.9500 i & - 0.8900 + 2.9500 i \\ 0.3500 + 3.8800 i & 1.1600 + 3.4500 i & - 0.0900 + 4.5500 i & 0.2000 + 3.1100 i \\ - 0.8700 + 3.2400 i & - 0.1600 + 2.9700 i & - 0.9700 + 3.4000 i & - 0.9800 + 3.3600 i \\ - 1.0200 + 4.0100 i & - 0.3100 + 3.6600 i & - 1.8800 + 4.3100 i & - 0.6600 + 3.9000 i \end{matrix}),$

求其唯一最小范数perhermitian解。

选取初始矩阵

$X_{1} (1) = 10^{3} \times (\begin{matrix} 2.2322 + 0.0000 i & 2.4950 - 0.4177 i & 1.8794 - 0.1577 i \\ 2.4950 + 0.4177 i & 2.8320 + 0.0000 i & 2.2000 + 0.1784 i \\ 1.8794 + 0.1577 i & 2.2000 - 0.1784 i & 1.5266 + 0.0000 i \end{matrix}),$

$X_{2} (1) = 10^{3} \times (\begin{matrix} 2.3482 + 0.0000 i & 1.6111 - 0.3890 i & 1.7942 - 0.0223 i \\ 1.6111 + 0.3890 i & 1.2291 + 0.0000 i & 1.2886 + 0.3338 i \\ 1.7942 + 0.0223 i & 1.2886 - 0.3338 i & 1.4593 + 0.0000 i \end{matrix}),$

根据算法3.1，经过19步迭代终止，得到该矩阵方程的唯一最小范数perhermitian解：

$X_{1} (19) = 10^{3} \times (\begin{matrix} 4.4633 + 0.0000 i & 4.9899 - 0.8353 i & 3.7589 - 0.3154 i \\ 4.9899 + 0.8353 i & 5.6630 + 0.0000 i & 4.4000 + 0.3567 i \\ 3.7589 + 0.3154 i & 4.4000 - 0.3567 i & 3.0522 + 0.0000 i \end{matrix}),$

$X_{2} (19) = 10^{3} \times (\begin{matrix} 4.6953 + 0.0000 i & 3.2223 - 0.7781 i & 3.5884 - 0.0445 i \\ 3.2223 + 0.7781 i & 2.4572 + 0.0000 i & 2.5773 + 0.6675 i \\ 3.5884 + 0.0445 i & 2.5773 - 0.6675 i & 2.9175 + 0.0000 i \end{matrix}),$

并且，相应残差的范数 $r = 4.4335 \times 10^{- 12} < 10^{- 10}$ 。

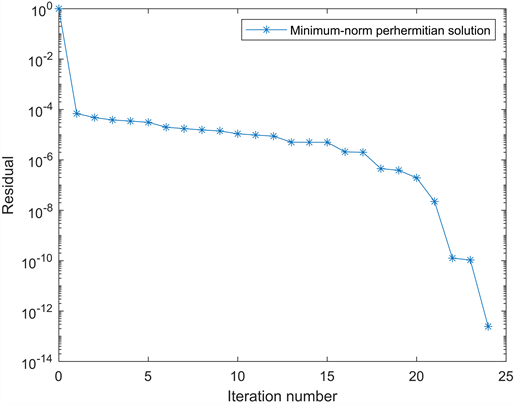
Figure 1. Convergence curves for Example 4.1

图1. 例4.1的收敛曲线

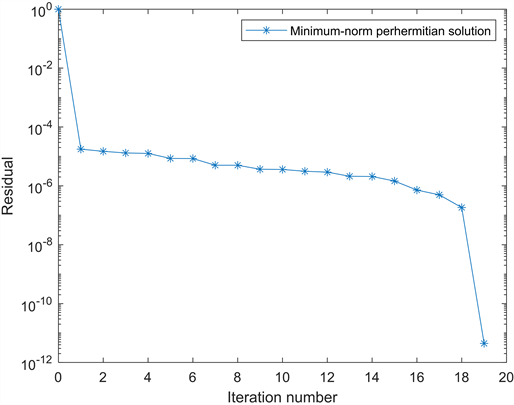
Figure 2. Convergence curves for Example 4.2

图2. 例4.2的收敛曲线

上述两个例子表明，我们的方法能够有效的获得Sylvester矩阵方程组的唯一最小范数perhermitian解。此外，从图1和图2可以看出，算法在数值上是非常可靠的。

5. 总结

在本文中，我们利用BCR算法来求解Sylvester矩阵方程组(1.1)的perhermitian解。我们证明了算法是收敛的，在不存在舍入误差的情况下，可以在有限步内得到唯一的最小范数perhermitian解。最后，通过两个算例说明了算法的可行性和有效性。

文章引用

唐孝伟,李胜坤. BiCR算法求解Sylvester矩阵方程组的Perhermitian解
The BiCR Algorithm for Solving the Perhermitian Solutions of Sylvester Matrix Equations[J]. 应用数学进展, 2023, 12(12): 4967-4986. https://doi.org/10.12677/AAM.2023.1212489

参考文献

1. Petkov, P.H., Christov, N.D. and Konstantinov, M.M. (1991) Computational Methods for Linear Control Systems. Pren-tice-Hall, Hoboken, USA.

2. Helmke, U. and Moore, J. (1996) Optimization and Dynamical Systems. Proceedings of the IEEE, 84, 907. https://doi.org/10.1109/JPROC.1996.503147

3. 程云鹏, 张凯院, 徐仲. 矩阵论[M]. 第3版. 西安: 西北工业出版社, 2006.

4. 张晓宁. 约束矩阵方程求解的交替投影算法及其在图像恢复中的应用[D]: [硕士学位论文]. 桂林: 桂林电子科技大学, 2015.

5. 杨清宇, 马训鸣, 朱洪艳. 现代控制理论[M]. 西安: 西安交通大学出版社, 2013.

6. 孙志忠, 袁慰平, 闻珍初. 数值分析[M]. 第3版. 南京: 东南大学出版社, 2010.

7. Hu, D.Y. and Reichel, L. (1992) Krylov-Subspace Methods for the Sylvester Equation. Linear Algebra and Its Applications, 172, 283-313. https://doi.org/10.1016/0024-3795(92)90031-5

8. El Guennouni, A., Jbilou, K. and Riquet, A.J. (2002) Block Krylov Subspace Methods for Solving Large Sylvester Equations. Numerical Algorithms, 29, 75-96. https://doi.org/10.1023/A:1014807923223

9. Beik, F.P.A. and Salkuyeh, D.K. (2011) On the Global Krylov Subspace Methods for Solving General Coupled Matrix Equations. Computers & Mathematics with Applications, 62, 4605-4613. https://doi.org/10.1016/j.camwa.2011.10.043

10. Bouhamidi, A., Hached, M., Heyouni, M. and Jbi-lou, K. (2013) A Preconditioned Block Arnoldi Method for Large Sylvester Matrix Equations. Numerical Linear Algebra with Applications, 20, 208-219. https://doi.org/10.1002/nla.831

11. Kaabi, A., Toutounian, F. and Kerayechian, A. (2006) Preconditioned Galerkin and Minimal Residual Methods for Solving Sylvester Equations. Applied Mathematics and Computation, 181, 1208-1214. https://doi.org/10.1016/j.amc.2006.02.021

12. 徐冬梅, 鲍亮, 蔡兆克. 预条件Krylov子空间法求解耦合Sylvester矩阵方程[J]. 华东理工大学学报(自然科学版), 2015, 41(6): 871-876.

13. Dehghan, M. and Hajarian, M. (2008) An Iterative Algorithm for the Reflexive Solutions of the Generalized Coupled Sylvester Matrix Equations and Its Optimal Approximation. Applied Mathematics and Computation, 202, 571-588. https://doi.org/10.1016/j.amc.2008.02.035

14. Dehghan, M. and Hajarian, M. (2010) An Iterative Method for Solving the Generalized Coupled Sylvester Matrix Equations over Generalized Bisymmetric Matrices. Applied Mathe-matical Modelling, 34, 639-654. https://doi.org/10.1016/j.apm.2009.06.018

15. Dehghan, M. and Hajarian, M. (2010) The General Coupled Matrix Equations over Generalized Bisymmetric Matrices. Linear Algebra and Its Applications, 432, 1531-1552. https://doi.org/10.1016/j.laa.2009.11.014

16. Dehghan, M. and Hajarian, M. (2010) An Efficient Algorithm for Solving General Coupled Matrix Equations and Its Application. Mathematical and Computer Modelling, 51, 1118-1134. https://doi.org/10.1016/j.mcm.2009.12.022

17. Lv, C.Q. and Ma, C.F. (2018) BCR Method for Solving General-ized Coupled Sylvester Equations over Centrosymmetric or Anti-Centrosymmetric Matrix. Computers & Mathematics with Applications, 75, 70-88. https://doi.org/10.1016/j.camwa.2017.08.041

18. Hajarian, M. (2016) Symmetric Solutions of the Coupled Gener-alized Sylvester Matrix Equations via BCR Algorithm. Journal of the Franklin Institute, 353, 3233-3248. https://doi.org/10.1016/j.jfranklin.2016.06.008

19. Yan, T.X. and Ma, C.F. (2020) The BCR Algorithms for Solving the Reflexive or Anti-Reflexive Solutions of Generalized Coupled Sylvester Matrix Equations. Journal of the Franklin Institute, 357, 12787-12807. https://doi.org/10.1016/j.jfranklin.2020.09.030

20. Hill, R.D., Bates, R.G. and Waters, S.R. (1990) On Perhermit-ian Matrices. SIAM Journal on Matrix Analysis and Applications, 11, 173-179. https://doi.org/10.1137/0611011

21. Pressman, I.S. (1998) Matrices with Multiple Symmetry Properties: Applica-tions of Centrohermitian and Perhermitian Matrices. Linear Algebra and Its Applications, 284, 239-258. https://doi.org/10.1016/S0024-3795(98)10144-1

22. Wu, A.G. and Zhang, Y. (2017) Complex Conjugate Matrix Equations for Systems and Control. Springer, Singapore. https://doi.org/10.1007/978-981-10-0637-1

23. Wu, A.G., Feng, G., Duan, G.R. and Wu, W.J. (2010) Iterative Solutions to Coupled Sylvester-Conjugate Matrix Equations. Computers & Mathematics with Applications, 60, 54-66. https://doi.org/10.1016/j.camwa.2010.04.029

24. Liang, K. and Liu, J. (2011) Iterative Algorithms for the Mini-mum-Norm Solution and the Least-Squares Solution of the Linear Matrix Equations , . Applied Mathematics and Computation, 218, 3166-3175. https://doi.org/10.1016/j.amc.2011.08.052

25. Peng, Y.X., Hu, X.Y. and Zhang, L. (2005) An Iteration Method for the Symmetric Solutions and the Optimal Approximation Solution of the Matrix Equation . Applied Math-ematics and Computation, 160, 763-777. https://doi.org/10.1016/j.amc.2003.11.030

26. Peng, Z.Y., Wang, L. and Peng, J.J. (2012) The Solutions of Ma-trix Equation over a Matrix Inequality Constraint. SIAM Journal on Matrix Analysis and Applications, 33, 554-568. https://doi.org/10.1137/100808678

NOTES

^*通讯作者。

期刊菜单