Open Journal of Nature Science
Vol.05 No.01(2017), Article ID:19720,13
pages
10.12677/OJNS.2017.51007
On the Origin of the Shangyuan Jinian Period-Since-Grand-Epoch
Yixun Wang
College of Mathematics Science, Suzhou University, Suzhou Jiangsu

Received: Jan. 24th, 2017; accepted: Feb. 10th, 2017; published: Feb. 16th, 2017

ABSTRACT
On the base of the inner logicality of the Number Theory, this article examines the source and calculation of the Santong Calendar (7 B.C.) by Liu Xin, and points out that the origin of the Shangyuan Jinian Period-Since-Grand-Epoch, used during 1500 years in ancient China, is just that “there are 300 days plus 6 periods of ten days and plus 6 days in one year” in the time of Yao and Shun about 4400 years ago.
Keywords:Origin, Ancient Chinese Calenders, Period-Since-Grand-Epoch, Number Theory
上元积年本原探索
王翼勋
苏州大学数学科学学院,江苏 苏州
收稿日期:2017年1月24日;录用日期:2017年2月10日;发布日期:2017年2月16日

摘 要
依据数论发展的内在逻辑,本文分析公元前7年刘歆三统历的起因和计算,指出古代中国流行1500多年的上元积年,本原就是约4400多年前尧舜的“岁三百有六旬有六日”。
关键词 :本原,中国古代历法,上元积年,数论

Copyright © 2017 by author and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
1.1. 历数
远古的人们,采集渔猎,探索植物生长成熟、动物活动,认识到气候变化与月亮圆缺;以农牧为主,掌握农时,必须对天象作尽可能精细的观察。为观察天体运行,古人以太阳一日行一度,积累数据,形成历数。班固《汉书∙律历志》三统历 [1] 以历数开宗明义。司马迁《史记∙历书》也有类似论述。
夫历《春秋》者,天时也,列人事而因以天时。……是以事举其中,礼取其和,历数以闰正天地之中,以作事厚生,皆所以定命也。……
历数之起上矣。传述颛顼命南正重司天,火正黎司地,其后三苗乱德,二官咸废,而闰余乖次,孟陬殄灭,摄提失方。尧复育重、黎之后,使纂其业,故《书》曰:“乃命羲、和,钦若昊天,历象日月星辰,敬授民时。”“岁三百有六旬有六日,以闰月定四时成岁,允厘百官,众功皆美。”其后以授舜曰:“咨尔舜,天之历数在尔躬。”舜亦以命禹。至周武王访箕子,箕子言大法九章,而五纪明历法。故自殷、周,皆创业改制,咸正历纪,服色从之,顺其时气,以应天道。三代既没,五伯之末,史官丧纪,畴人子弟分散,或在夷狄,故其所记,有黄帝、颛顼、夏、殷、周及鲁历。
尧、舜、禹视历数为立国之本,代代相传。周武王灭商建周,访殷代遗贤,箕子呈上“五纪明历法”的“大法九章”。三国曹魏时孟康说,“五纪”指岁月日星辰。唐颜师古说,“大法九章”是《洪范》九畴,九畴中“三曰农用八政,四曰协用五纪。”历数一词,为唐孔颖达《左传》恒公十七年《疏》所明确:“晦朔弦望交会有期,日月五星行道有度。历而数之,故曰历数也。”日行一度,以东汉《续汉书·律历志下》描述最详 [2] :“天之动也,一昼一夜而运过周,星从天而西,日违天而东,日之所行与运周,在天成度,在历成日。”这个认识,朴素直观,背后闪烁着整数对辗转相除序列现象的迷人光芒。据四分历(85年)“周天度”之说,我们称太阳一岁这一圈为天度圈。天度圈概念在中国历法史上的实践意义和理论意义,无论怎样估计都不会过高。
1.2. 上元积年
古代历法家为推算二十四气、朔望、日月食的便利,往往需要设置一个整部历法的总起算点,称作上元。学术界公认,公元前7年刘歆明确引入上元积年概念,并实际计算了三统历上元积年数据。从《乾象历》(223年)起,八十余家历法都列出上元以来积年数据,作为历法第一条数据,直到元郭守敬《授时历》(1280年)才予废止。历法是皇权的象征,在中国封建社会中享有至高无上的地位。一千多年中,上元积年算法曾盛极一时,又戛然消亡,凝聚着一代代先哲的智慧和艰辛。
1.3. 三统历
古六历至今只存一些零星材料。黄帝、颛顼、夏、殷、周、鲁之名,始见于公元一世纪《汉书∙律历志》。四世纪初司马彪《续汉书∙律历志》给出六历上元甲子。《大唐开元占经》,才出现六历完整的上元干支和积年。
刘歆根据太初历改编的三统历,是我国第一部有完整术文传世的历法。今人得知三统历详情,全凭公元一世纪班固所撰《汉书》。班固这样介绍刘歆:“至元始中,王莽秉政,欲耀名誉,征天下通知钟律者百余人,使羲和刘歆等典领条奏,言之最详。故删其伪辞,取正义著于篇。”东汉顺帝汉安二年(143年)尚书侍郎边韶上言改历,提到三统历:“刘歆研机极深,验之《春秋》,参以易道,以《河图帝览嬉》、《雏书乾耀度》推广九道,百七十一岁进退六十三分,百四十四岁一超次,与天相应,少有阙谬。”清代钱大昕、李锐、董祐诚、陈澧、成蓉镜等学者,或重在正伪舛、脱误、去衍,或重在详细解释基本数据,或重在以本法推算、算术缀之,多方位研究三统历。近代,多少学者更从历史学、现代天文学、考古学、数学、考据学等多个学术角度,反复耕耘这些史料,然而困难重重,难以取得一致认识。
2. 天象观察呼唤数学
2.1. 日月五星的观测
古人对日月五星运行的认识,以杨伟景初历 [3] (237年)推五星术,最为完整。原文为:
五星者,木曰岁星,火曰荧惑星,土曰填星,金曰太白星,水曰辰星。凡五星之行,有迟有疾,有留有逆。曩自开辟,清浊始分,则日月五星聚于星纪。发自星纪,并而行天,迟疾留逆,互相逮及。星与日会,同宿共度,则谓之合。从合至合之日,则谓之终。各以一终之日与一岁之日通分相约,终而率之,岁数岁则谓之合终岁数,岁终则谓之合终合数。
地上的人们观察天体运行,以目测两个天体视相交,最为可靠。这在数学上,属于两球同心圆周运动问题。可以把从圆心出发看到的两球视线重叠,说成看到双交点。同样,把两球视线重叠于某背景点,说成看到两球、背景点的三交点,等价的说法,就是两球、圆心三点共线。一天体从某背景点出发,回到原处,称为恒星周期,周天一个圈。两天体从某相交点出发,到再次相交,前后两个双交点界定会合周期。前后两个三交点,界定大周,同时界定两天体各自周天圈数,形成多会合周期的集合。每个会合周期长度,等于大周总时间除以两周天圈数之差。
利用今天熟悉的指针钟面,可以形象地解释恒星周期和会合周期。分针、时针交于钟面正上方数字12处,体现三交点。时针转1圈12个小时,分针转1圈1个小时,体现不同的恒星周期。两针相交为双交点,前后双交点界定会合周期。前后两个三交点,界定大周12小时,同时界定背景上两针各自的1
圈和12圈。圈数之差11,11个双交点分隔12小时成11个会合周期。每个会合周期长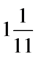 小时。
小时。
古传岁星12年11见。12年中,太阳12圈,岁星1圈。由圈数之差,12年11个交点,分成11个会合周期。用12个岁实除以11个会合周期,就是会合周期长度。
2.2. 人造行星数例
1962年华罗庚以人造行星、地球绕太阳运行为例 [4] ,深入浅出介绍,怎样估算人造行星发射后,再次接近地球的时间。我们在括号中加注基准圈(与天度圈有别),简述如下。
假定,地球绕太阳一圈(基准圈1年。太阳视运动为1年)360天(基准圈的划分),人造行星绕太阳一
圈450天。因450和360最小公倍数是1800,或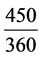 =
= 。5年后,人造行星走4圈,再次接近地球。地球绕太阳一圈,重新划分成
。5年后,人造行星走4圈,再次接近地球。地球绕太阳一圈,重新划分成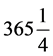 天(基准圈的划分)。人造行星仍然是绕一圈450天。顺便说说,因基准圈的划分不同,两个450天时长不等。以
天(基准圈的划分)。人造行星仍然是绕一圈450天。顺便说说,因基准圈的划分不同,两个450天时长不等。以 天做单位,绕太阳一圈各为1800和1461单位。辗转相除得商1、4、3、4、2、1、2。可以排出连分数
天做单位,绕太阳一圈各为1800和1461单位。辗转相除得商1、4、3、4、2、1、2。可以排出连分数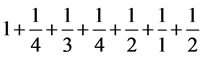 ,逐次删除尾部得1,
,逐次删除尾部得1,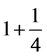 =
= ,
, 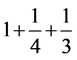 =
=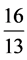 ,
, 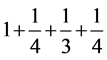 =
=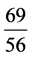 ,
,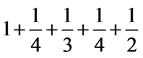 =
= ,……。
,……。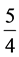 表示5年后人造行星4圈,接近地球。
表示5年后人造行星4圈,接近地球。 说明16年后人造行星13圈,精密些。
说明16年后人造行星13圈,精密些。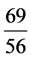 说明69年后人造行星56圈,更为精密。
说明69年后人造行星56圈,更为精密。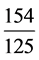 的精密程度自然更好。观察原分数
的精密程度自然更好。观察原分数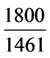 的渐近分数序列
的渐近分数序列 、
、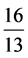 、
、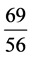 、
、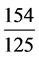 ,…,我们意识到,古人可能
,…,我们意识到,古人可能
把分子、分母位数庞大的分数,简化成位数较少的渐近分数,以满足历法编排的需要。吕子方所说日法81、木星大周1728,就源于此。
2.3. 连分数与密近简化
1951年吕子方 [5] “以科学实测为基础,以探讨三统历法,故第一章统母、第二章纪母,纯以实测及古传数字为出发点,以求所用基本数字之来源。如日法八十一,木星大周年数为一千七百二十八等是也。”何鲁为之作序,盛赞吕子方:“析以新法,洞中窾要,尤能明古人之用心,使二千年前之成绩焕然一新,厥功甚伟。”此说引起学术界热议,但以连分数,逐次删除尾部,形成渐近分数系列,直接描述二千年前的数值计算,充其量涉及存在性,未涉及构造性,不免难以迅速获得公认。
秦九韶“早岁侍亲中都,因得访习于太史,又尝从隐君子受数学”,在1247年《数书九章》中为我们留下了治历演纪题 [6] 。这是上元积年行用期间,讲述数值解法的唯一史料。完全可以肯定,作为上元积年算法的晚期形态,1208年的开禧历,深深地刻着发展进程的烙印。秦九韶刻划过上元积年与元之间的数理关系:“奇余取策,群数皆捐。衍而究之,探隐知原”。以元度量从上元至近期编历岁岁首的总时段,得到元个数与余数,数学上属于带余除法。根据元周期长度和余数,反求元的个数,数学上属于求解线性同余式。
1208年的求乘率筹算原图,涉及到三阶段的整数对辗转相除序列现象:两整数辗转相除得一系列商,为第一阶段。第二阶段计算的只是单组Q序列值。第三阶段依据某条件,关联某Q序列值为所需的乘率。此时的入算两整数,或为线性不定方程两系数,或为线性同余式系数与模,或来自传统数学满去式,参见第5.5节。数论教科书上有个定理 [7] ,描述P、Q序列两组共存,沟通整数对及其最大公约数。两个正整数a、b不必互素,不妨约定a不小于b,辗转相除,每一步都能找到P序列值、Q序列值的线性组合,等于正负号交替的相关余数,总有一步,等于最大公约数。
序列值线性组合定理 若a、b是任意两个正整数,
Qka−Pkb = (−1)k−1rk, k = 1, 2, …, n,
其中, P0 = 1, P1 = q1, Pk = qkPk−1 + Pk−2, k = 2, …, n,
Q0 = 0, Q1 = 1, Qk = qkQk−1 + Qk−2, k = 2, …, n。
考察连分数逐次删除尾部,所形成的渐近分数系列,每个渐近分数的分子、分母,是同一商qk相关的Pk、Qk序列值。其实,只要算出序列值,就可以取出同一个商的两个序列值,组成与两原整数之比近似的分数了。根据三统历大周的历法大背景,我们不妨称为密近简化值,密近指与原比值之差的微小程度,简化特指分子分母位数的减少。史料上的1208年筹算图,只计算单组Q序列值,但完全能算P序列值,因为1801年高斯在《算术研究》27节中,就以同一组序列值公式,表达Q序列和P序列。不能不指出,开禧历处于三统历之后1215年。依据开禧历史料所作分析,恐怕只是我们的臆想。如果没有在三统历中找到以岁星岁数为代表的大周概念,我们真不知道怎样跨越一千二百多年的漫长时光,去证明公元之初的刘歆,已经知晓密近简化计算。天象观测呼唤数学,推动数学,反过来,数学进步又深化了人们对天象的认识。
我们相信,以开禧历、三统历相关史料为基础,依据整数对辗转相除序列现象内在逻辑,一步步向远古探索,有可能追溯上元积年的本原。
3. 岁星超辰
刘歆应用12岁11见的古传岁星纪年,算出一见之值。以日为率,进行相约,密近简化,导出1728岁1583见的岁星大周。再导出岁星日行率与岁星超辰 [8] 。
3.1. 岁星大周的推导
3.1.1. 一见的推算
日出时岁星现于东方地平线,为岁星与太阳视相交,称重合。再次重合,刘歆称一见。
三统历岁实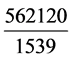 ,一见
,一见 日 ≈
日 ≈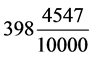 日(今值398.88日)。刘歆采用
日(今值398.88日)。刘歆采用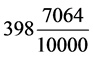 日(人为调高了
日(人为调高了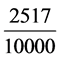 日)。在三统历第三章五步中,记列的是
日)。在三统历第三章五步中,记列的是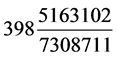 日(约
日(约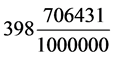 日)。
日)。
3.1.2. 相约算法
可以认定,三统历虽无相约二字,却使用了相约算法。景初历(237年)说的“以一终之日与一岁之日通分相约”,在东汉四分历(85年)就出现了:“五星之数生也,各记于日,与周天度相约而为率。”
以日为率。一日中,岁星与太阳重合1/398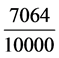 次。写年换日,扩大
次。写年换日,扩大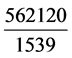 倍。一年中,重合
倍。一年中,重合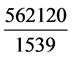 /
/ =
=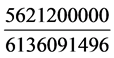 次。可以说成,每6,136,091,496年,岁星与太阳重合5,621,200,000次。
次。可以说成,每6,136,091,496年,岁星与太阳重合5,621,200,000次。
3.1.3. 计算细节
我们采用序列值计算表,计算6,136,091,496和5,621,200,000如表1。
刘歆发现1728是12的144倍,与《周易∙系辞》的“坤之策百四十有四”相符。在纪母中明确坤(巛)策144:“木金相乘为十二,是为岁星小周。小周乘巛(坤字古体)策,为千七百二十八,是为岁星岁数。”把1728年认作岁星岁数,1583次认作见数,密近于6,136,091,496年5,621,200,000见,两者数值相差0.00000007。分子分母简化成四位,有利于历法编排。12年11见,相约所得6,136,091,496年5,621,200,000见,及密近简化调出的1728年1583见,三组值都是岁星大周,从日出时岁星现于东方地平线上某背景点,到此天象再次出现。一般地说,同一序列中较大的值,除非刻意凑合,不可能是较小值的倍数。不
刻意取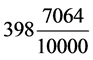 日,无法算出1728是12的144倍。
日,无法算出1728是12的144倍。
Table 1. Sequence calculation of 6,136,091,496 and 5,621,200,000
表1. 6,136,091,496与5,621,200,000序列值计算表
3.2. 日行率和超辰
岁星1728年1583见,走145周天。每年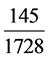 周天。每日
周天。每日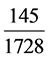 度,就是岁星日行率。
度,就是岁星日行率。
1728年有12个144年,1周天分12星次。岁星1728年走145周天145 × 12星次,平摊到144年,岁星行145次,比144年古传位置144次,超一次。
中国历法史上绝无仅有的岁星超辰,就是这样诞生的。
3.3. 太极上元
刘歆以太初历“上元泰初四千六百一十七岁”为基础,逐级构建体现乾坤之策的“太极上元”,作为三统历的最高境界。
首先构建“五星会终”138,240年,以特殊推一般:“天以一生水,地以二生火,天以三生木,地以四生金,天以五生土。五胜相乘,以生小周,以乘乾坤之策,而成大周”。五胜相乘,得五星小周。小周分别乘上《周易∙系辞》的“乾之策二百一十有六,坤之策百四十有四”,得大周。木星1728年的80大周、火星13,824年的10大周、土星4320年的32大周、金星3456年的40大周或水星9216年的15大周,都是138,240年。
然后“乘章岁”,138,240 × 19 = 2,626,560,“与日月会”,三会3 × 2,626,560 = 7,879,680,为一统。三统3 × 7,879,680 = 23,639,040。“太极运三辰五星于上,而元气转三统五行于下。其于人,皇极统三德五事。故三辰之合于三统也,日合于天统,月合于地统,斗合于人统。…五星会终…与日月会… 与三统会。三统二千三百六十三万九千四十,而复于太极上元。”
在刘向多年研究的基础上,刘歆对作为整部历法支柱的元,有着深刻的了解。
无疑,为谋取太极上元与太初上元起始点天象相同,必须使23,639,040年含有5120个太初元(23,639,040 = 4617 × 5120),一定是费了一番周折的。
4. 元的构建
4.1. 两历基准
太初历的改历充满着矛盾 [9] 。基准数据中,并无积年之说,只有单个元4617岁:
乃以前历上元泰初四千六百一十七岁,至于元封七年,复得阏逢摄提格之岁,中冬十一月甲子朔旦冬至,日月在建星,太岁在子,已得太初本星度新正。
太初历侧重太岁。据汉人所编分类词典《尔雅∙释天》,“阏逢摄提格”为太岁纪年名之一,对应甲寅。“太岁在子”,子只是十二地支之首。刘歆侧重岁星,首创岁星超辰,改造成三统历。
汉历太初元年,距上元十四万三千一百二十七岁。前十一月甲子朔旦冬至,岁在星纪婺女六度,故《汉志》曰:岁名困敦,正月岁星出婺女。
元的界定点维持不动,为“前”十一月(太初称“中冬”十一月)甲子日夜半朔旦冬至。
4.2. 元的确立
历家选定若干周期,依某些算法,构建成元,这是所谓运算转历的第一步。
《续汉书·律历志中》强调,确定元的组成在先,定日法的值等等在后:“太史令虞恭、治历宗䜣等议:建历之本,必先立元,元正然后定日法,法定然后度周天以定分、至。三者有程,则历可成也。”
4.3. 四分元的构建
《续汉书·律历志下》记述的四分术,选用岁实、朔望月、日名干支周期和岁名干支周期四项,用周期齐同算法,逐步构建章、蔀、纪、元。
岁首至也,月首朔也。至朔同日谓之章,同在日首谓之蔀,蔀终六旬谓之纪,岁朔又复谓之元。是故日以实之,月以闰之,时以分之,岁以周之,章以明之,蔀以部之,纪以记之,元以原之。然后虽有变化万殊,赢朒无方,莫不结繋于此而禀正焉。
约定第一岁岁首冬至与第一个朔望月月首同处起始点。岁实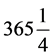 日与朔望月
日与朔望月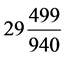 日齐同成章19岁(=
日齐同成章19岁(=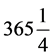 日 × 19 =
日 × 19 =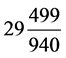 日 × 235 =
日 × 235 =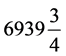 日),冬至朔旦一会“至朔同日”,并非夜半。寻求日的完整,齐同成蔀76岁(=
日),冬至朔旦一会“至朔同日”,并非夜半。寻求日的完整,齐同成蔀76岁(=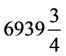 日 × 4 = 19岁 × 4),冬至合朔“同在日首”夜半。寻求日名干支周期完
日 × 4 = 19岁 × 4),冬至合朔“同在日首”夜半。寻求日名干支周期完
整而齐同成纪1520岁(=76岁 × 20 = 555,180日 = 60日 × 9253日名干支周期),甲子日零时冬至朔旦一会,称“蔀终六旬”,60日周而复始。寻求岁名干支周期完整而齐同成元4560岁(=1520岁 × 3 = 60岁 × 76岁名干支周期),甲子岁甲子日零时冬至朔旦一会。称“岁朔又复”,60岁周而复始。
4.4. 太初元的构建
流传至今的落下闳史料,寥寥无几。公元前104年,汉武帝为改历,先后下过七次诏书,两次与落下闳直接相关。第四次诏是接到大典星射姓等人奏报“不能为算”之后,另选多人编算新历。于是有落下闳的出场。“乃选治历邓平及长乐司马可、酒泉候宜君、侍郎尊及与民间治历者,凡二十余人,方士唐都、巴郡落下闳与焉。都分天部,而闳运算转历。”第七次诏,等校者太监淳于陵渠回奏,称邓平历法最密后,诏定用邓平法,且给邓平加官。本来,改历大事,功成名就,邓平加官,顺理成章。落下闳却“拜侍中,辞不受”,留下一言:“后八百岁,此历差一日,当有圣人定之。”《汉书》载“闳运算转历,其法以律起历”。司马迁也有“巴落下闳运算转历”之说。可见,落下闳以日法81、19岁7闰、日名干支周期60日,定太初元4617年。算法如下:
1) 密近简化。吕子方推测,落下闳以古六历朔策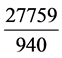 日 =
日 = 日作源,以连分数算出太初历的
日作源,以连分数算出太初历的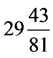 日 =
日 = 日。我们只是把连分数之说,换成等价的密近简化。我们无法了解落下闳计算探索的
日。我们只是把连分数之说,换成等价的密近简化。我们无法了解落下闳计算探索的
具体细节,只能列出序列值计算表2如下。表中的81,为3的倍数。落下闳提出“律容一龠,积八十一寸,则一日之分也”,是因为汉时人们对音律的认识,主要是三分损益律。太初历、三统历的历法数值,基本都与3有关。依据汉武帝第五次诏书,后世学者认定,八十一分律历为邓平所造。
2) 写岁换分。由81 × 19 = 1539分,写岁换分,1539分成为1539岁。
3) 写日换分。1章19岁7闰235历月,月分2392分。1章2392 × 235 = 562,120分。写日换分,成为56,2120日。分摊到1539岁,岁实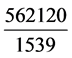 日 =
日 = 日。
日。
4) 齐同算法。三倍562,120日,才是日名干支周期60日的28,106倍。故1539岁 × 3 = 太初元4617年。
5) 交食循环、日月合璧。一章235个朔望月和135月日食周期两个实测周期的齐同,有235月 × 27 = 135月 × 47 = 6345月 =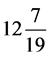 月 × 513。一会513岁,九倍为太初元4617年。这正是定日法81的有力支柱。
月 × 513。一会513岁,九倍为太初元4617年。这正是定日法81的有力支柱。
Table 2. Sequence calculation of 940 and 499
表2. 940和499序列值计算表
这里也印证了虞恭、宗䜣所谓“必先立元,元正然后定日法”的说法。落下闳所创这一系列算法,是中国千年历法计算的中流砥柱。
4.5. 三统元的构建
刘歆另辟蹊径,以日法81与章岁19之积1539为统法,写岁换分,定出统1539岁,三个统4617年,构建三统元。4617年含日名干支周期28,106个。三个统分别命名天统甲子、地统甲辰、人统甲申,源于各自的统首日,分别为甲子(0)、甲辰(40)、甲申(20)。
5. 上元积年的构思
中国历法起步于天度圈观念,必走上元积年之路。岁星超辰与天象明显不符,却在上元积年求索的过程中,起过重大的推动作用。
5.1. 六条上元积年值
只是在《世经》中,才出现上元积年值。这六条值按先后次序,编号如下:
(一) 上元至伐桀之岁,十四万一千四百八十岁,岁在大火房五度。
(二) 上元至伐桀十三万二千一百一十三岁,其八十八纪,甲子府首,入伐桀后百二十七岁。
(三) 上元至伐纣之岁,十四万二千一百九岁,岁在鹑火张十三度。
(四) 厘公五年正月辛亥朔旦冬至,《殷历》以为壬子,距成公七十六岁。是岁距上元十四万二千五百七十七岁,得孟统五十三章首。
(五) 汉高祖皇帝,著《纪》,伐秦继周。木生火,故为火德。天下号曰“汉”。距上元年十四万三千二十五岁,岁在大棣之东井二十二度,鹑首之六度也。故《汉志》曰:岁在大棣,名曰敦牂,太岁在午。
(六) 汉历太初元年,距上元十四万三千一百二十七岁。前十一月甲子朔旦冬至,岁在星纪婺女六度,故《汉志》曰:岁名困敦,正月岁星出婺女。
以第六条上元至太初元年的值作基准,变动近期编历岁,可推出第一、三、四、五条。第二条上元至伐桀,采用四分纪1520岁,但并非四分历上元积年,而是试图融入岁名干支周期。
5.2. 世经意图
刘歆作世经,“以说《春秋》”。班固说过:“至孝成世,刘向总六历,列是非,作五纪论。向子歆,究其微眇,作三统历及谱,以说春秋,推法密要,故述焉。”三统历分七章:一统母,二纪母,三五步,四统术,五纪术,六岁术,七世经。统母、纪母为立法之源,五步乃五星会合周期动态段研究,统术、纪术、岁术是推算日月五星及岁星所在之次,而《世经》乃是刘歆对古史归纳而成的一份年谱。从年代学的角度来考虑,上古史料本来零乱,越往古,王朝的年代越难断定。例如关于周武王伐纣的年代,历代研究提出的年份,至少有数十家。刘歆所说,也算其中一家。岁星纪年法行用期间,古人著书录入当时所见岁星所在,总以实际观察为准。12个星次划分明确,岁星位置清晰可辩,应该并无多大观察误差。《世经》不符合岁星11.86年一周天、约86岁超出一次的真实规律。所载古传史料中的岁星纪年和朔旦冬至,古之纪年条款,除少数用殷历、周历外,大部分用三统历岁术推算过,体现144年超一次。
5.3. 推岁所在之术
推岁所在之术的要点,是算某年月日的岁星所在。从上元到此刻,岁星所行总星次满去周天12星次,所得积次、次余,即可估岁所在星次与宿。也可先“盈岁数,除去之”,满去大周。原文如下:
推岁所在,置上元以来,外所求年,盈岁数,除去之,不盈者以百四十五乘之,以百四十四为法,如法得一,名曰积次,不盈者名曰次余。积次盈十二,除去之,不盈者名曰定次。数从星纪起,算尽之外,则所在次也。
以汉历太初元年143,127岁为例,满去岁星岁数1728岁。82个岁星大周之后,余1431岁,行1431 ×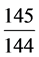 = 1440(积次)
= 1440(积次)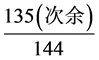 。积次1440次“盈十二”,恰为120周天。星纪处周天之首,则据次余135,估出岁星在星纪中的比例位置。星纪约30度,始于斗12度,终于婺女7度。由次余135,30度 ×
。积次1440次“盈十二”,恰为120周天。星纪处周天之首,则据次余135,估出岁星在星纪中的比例位置。星纪约30度,始于斗12度,终于婺女7度。由次余135,30度 ×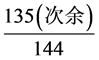 =
=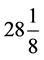 度。以比例考量,岁星位于星纪的
度。以比例考量,岁星位于星纪的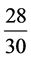 强,为婺女6度。
强,为婺女6度。
5.4. 构思探索
要探索刘歆引入上元积年的具体原因和构思细节,困难重重。1928年日本学者新城新藏开垦草莽,以线性四元不定方程进行推测,试算硬凑31个元。1980年袁向东、李文林推测 [10] ,推算三统上元之关键,是汉历太初元年……前十一月甲子朔旦冬至。把岁在星纪婺女六度,理解成处于30度星纪的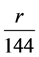 ,r在135与139 之间。
,r在135与139 之间。
如果以p、q为不定整数,q为岁星运行圈数,有线性不定方程:
4617 × p ×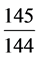 = 12 p +
= 12 p +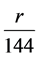 ,即669,465p = 1728 q + 135,
,即669,465p = 1728 q + 135,
相当于以x为未知数的线性同余式:
4617 × x ×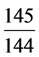 ≡
≡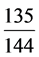 (mod 12),即669,465x ≡ 135 (mod 1728)。
(mod 12),即669,465x ≡ 135 (mod 1728)。
仅当余数r取整数135,即有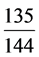 时,有最小正整数解x = 31。可算出上元积年数143,127。
时,有最小正整数解x = 31。可算出上元积年数143,127。
前辈们不畏艰难,披荆斩棘,开拓了我们的视野,鞭策着我们一步步前进。
我们赞成吕子方的推测,落下闳以古六历29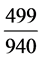 日作源,算出太初历29
日作源,算出太初历29 日。只把连分数之说换
日。只把连分数之说换
成等价的密近简化。又把袁向东、李文林推测中的669,465x ≡ 135 (mod 1728),换成等价的满去式:多少个669,465,满去1728,不满135。
在前辈基础上,我们不揣冒昧,根据编岁术和编世经的次序先后,提出一个新推测。三统上元积年如取31个元,依岁术可算得,岁在“星纪婺女六度”,与《汉志》所载相合,足以证明三统历的权威。31这个值,可能是在大量试算时遇到的,促使刘歆谋求用数值解法,利用元4617岁和余数“婺女六度”,反推算出这个值31。
这相当于考虑现今所说线性同余式问题:
岁星超辰运行,从上元起历经多少个4617岁,到太初元年处于“星纪婺女六度”(即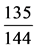 )?
)?
刘向父子积累了丰富的历法计算知识。刘歆推算岁星大周时,熟知落下闳把940、499,密近简化为81、43的计算过程。刘歆同时代的《九章算术》,已经明确有等数概念。第4.4节表2中算到除法12 = 11 × 1 + (r7)1。如果计算下一步,是11 = 1 × 10 + (r8)1。筹算板上下,(r8)1 = (r7)1,就是等数。落下闳取81,出于“以律起历”。刘歆可能根据等数1,注意到与81关联的43。如果能想到:多少个940,满去499,不满为1?再试算知:43个940为40,420,40,420扣除1,得到40,419,恰巧是499的81倍。也就有可能想到:多少个669,465,满去1728,不满135。
5.5. 数值解法
东、西方数学家,对整数对辗转相除序列现象的开发和利用,途径不同,形式也不同。我们理解1208年筹算图数理,推测公元前7年密近简化,依赖的是近代数论。绝对不能忽略,传统数学的数值解法,是筹算大背景下的产物。只有弄清等数的原文、原术、原意,等数在1208年求乘率术中起的作用,我们才能放心地从跨度几千年的史料中,寻找线索,探索上元积年的本原。
5.5.1. 整数对固有本性
一切整数对a、b,不妨约定a不小于b,都有其固有的数理本性。辗转相除过程中,首次出现的余数称为自然余数。一切整数对因自然余数除数序数的奇、偶不同,分成彼此独立的两大类。
约公元前300年的欧几里得的辗转相除法,求最大公约数时,把整除作为终止运算的标志,不涉及这个本性。1801年高斯《算术研究》27节,“通过求两个数最大公约数的已知算法”,处理线性不定方程ax = by + c两系数(线性同余式ax ≡ c(mod b)系数与模),“数值递降,直到m = μn + 1,这总是可以做到的”,从而涉及到整数对本性。高斯完善地解决了涉及整数对辗转相除序列的线性不定方程(同余式)求解问题 [11] 。
5.5.2. 求等数术
等数是筹算的产物。现存史料中的求等数术,有减法形式和除法形式两种,都以相等的两个值,作为终止运算的标志。《九章算术》约分术描述的是减法形式:“副置分母、子之数,以少减多,是更相减损,求其等也。以等数约之。”“求其等也”,追求两个数值的相等。“以等数约之”是数值运算,用以“约之”的最大公约数,是等数的值。以约简49/91为例。上下放置49和91,括号中是减数,各步构成示意图。见表3。更相减损终了,上下两个7相等,合称等数。约分子49,约分母91,用等数的值7。求等数术的除法形式,见于1208年开禧历求乘率术原图右列。我们以669,465(a)和1728(b)为例。为与求乘率术一致,先算669,465(a) = 1728(b) × 387(q1) + 729(r1)。再上下布列成示意图首图,暂且不记入商。求等数术除法形式,见表4示意图(图1-图6):递互除之终了,不采用整除除法189 = 81 × 3(q5),调节商3减1成2,形成189 = 81 × 2(q5) + 27(r5),27(r5)为自然余数。调节后除法为81 = 27 × 2(q6) + 27(r6),
Table 3. The schema for the seeking equal-numbers in subtractive form
表3. 求等数术减法形式示意图
Table 4. The schema for the seeking equal-numbers in division form
表4. 求等数术除法形式示意图
27(r6)称调节余数。依照原筹算图,对上下27和27各标一个等字,27(r5)为等数自然值27,27(r6)为等数调节值27。两个27才为等数。等数的值27才是669,465和1728的最大公约数。可以看到,自然余数、调节余数、等数自然值、等数调节值四项的值,都是最大公约数。当两个整数互素时,最大公约数的值就是1。求等数术以等数标志最大公约数,不区分自然值还是调节值,能完善处理两大类整数对。
5.5.3. 求乘率术
在求乘率时,等数标志乘率,直观简便,却经受不起这个本性的考验。
传统数学中的序列概念,源于筹算除法的“实如法而一”,商起统计除数个数的作用。随着整数对递互除之,除数不断细化,除数个数步步累积,反映序列公式Q0 = 0,Q1 = 1,Qk = qkQk−1 + Qk−2,k = 2,…,n。参见第2.2节。在求等数术除法形式首图左侧,增设天元一(Q1 = 1)和空(Q0 = 0),就成了求乘率术首图。为了求多少个669,465,满去1728,不满为135,我们模仿1208年筹算图求乘率。先算669,465(a) = 1728(b) × 387(q1) + 729(r1),再列成表5。顶行表示各数值的关系,第二行突出当前筹算的运算目标,最下一行标出筹算图序号(图1-图11)。图9上方除法81 = 27 × 2(q6) + 27(r6)中,商(q6)取2不取3,产生余数27(r6)。图10中上下27各标一个等字。到图11,两个相等的27,合为等数,标志左上19为乘率。等数标志乘率,直观简便,却为求乘率术埋下了数理缺陷。
高斯处理不定方程ax = by + c(同余式ax≡c(mod b)),c分正负,整数对a、b辗转相除,有自然余数分支和调节余数分支,共有四种情况。传统满去式:多少个a满去b不满c,由于余数c只取正,只有上述四种情况中的两种。筹算图特定的排法,导致运算终了,左上数总是乘率(序列值),右上数总是判断标志,这个数与作为乘率的序列值,属于同一余数分支。至于采用自然余数(等数自然值),还是采用调节余数(等数调节值),取决于整数对a、b的数理本性 [12] 。单独等数自然值,当自然余数除法序数为奇时,是取自然余数分支序列值的充分必要条件。单独等数调节值,当自然余数除法序数为偶时,是取调节余数分支序列值的充分必要条件。两个相等数合称的等数,只是充分不必要条件。这里利用为奇的具体数例进行解释。整数对669,465和1728自然余数(r5)除法序数(5)为奇,单独的右上等数自然值(r5)27,就是取自然余数分支序列值(Q5)19的充分必要条件。受困于追求等数,画蛇添足,必凑等数调节值(r6)27,必闯调节余数分支,必误求图11左下(Q6)45(调节余数分支序列值),并冲击右列上下轮流作被除数的规律。直到1247年,秦九韶大衍求一术处理互素整数对,“须使右上末后奇一而止。乃验左上所得,以为乘率”,这才完善地解决了满去式的求解问题,与高斯解法等价。
5.5.4. 满去式的解
求解多少个669,465,满去1728,不满135的全过程,可用开禧历求入元岁之术理,原文如下:
又以日法乘前历所测冬至气刻分,收弃末位为偶数,得斗分,与日法用大衍术入之,求等数、因率、蔀率,以纪乘等数为约率,置所求气定骨,如约率而一,得数,以乘因率,满蔀率去之,不满,以纪法乘之,为入元岁。
求乘率术算出等数27、因(乘)率19。开禧历的纪(纪法)源于干支周期60。此处纪(纪法)为1,约率等于等数27。约135得5,约1728得64。以乘率19乘5得95。95已是669,465 x ≡ 135 (mod 1728)的解。以95满去64所得的31,则是最小正整数解。
Table 5. Sequence calculation of 669,465 and 1728 in form of the original diagrams in 1208
表5. 模仿1208年筹算图计算669,465与1728
核算:669,465 × 31 = 20,753,415,20,753,415 − 135 = 20,753,280,20,753,280 = 1728 × 20,753,145。
大量数据试算中的偶然发现,碰撞到数理的内在逻辑,擦出的火花,引导刘歆求解线性满去式,成为上元积年计算第一人。闯入这个数学领域的刘歆,不会透彻了解其间数理,并未明确意识43、19为乘率。然而,所面临正反核算问题,以特定数值关系探索,还是能够解决的。
5.6. 欲知太岁之术
刘歆以统首日命名天统甲子、地统甲辰、人统甲申,已经注意到:4617年只含日名干支周期,不含岁名干支周期。《世经》第二条积年值“上元至伐桀十三万二千一百一十三岁,其八十八纪,甲子府首,入伐桀后百二十七岁”,并非四分上元积年,而是试图融入岁名干支周期。所谓甲子府首,指纪之首,四分历一纪1520岁含9253个日名干支周期。88纪共1520 × 88 = 133760 岁,扣除伐桀之岁到太初元年1647岁,所得132,113岁为上元到伐桀之岁。加入127,132,113 + 127 = 132,240 = 60 × 2204,有2204个岁名干支周期。故称“甲子府首,入伐桀后”127。至于融入岁名干支周期后的127,作何解释,不了了之。岁名干支周期注定成为岁星超辰绕不过的坎。刘歆无法回避太初历“太岁在子”之说,留下无法自圆其说的“欲知太岁”之术,原文是:
欲知太岁,以六十除积次,余不盈者,数从丙子起,算尽之外,则太岁日也。
首先,六十的单位不明。上元后经31个三统元,到太初元年4617 × 31 = 143127岁,无法以60整除。岁星超辰,4617 × 31 × =
=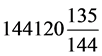 星次,扣除
星次,扣除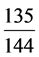 ,积次144,120尽管可以60整除,单位却是
,积次144,120尽管可以60整除,单位却是
星次。“数从丙子起”所说的丙子,属于六十干支周期。问题是,指干支纪日还是指干支纪年?现在所知,古以甲子纪日,干支纪年始见于西汉,多与岁名、岁在和丛辰配合使用,但始创时期,历代纪年关系,还未理顺,现存多例,互相抵牾。刘歆自成体系,是为一说。到东汉,才追正自西周共和以来历代各王世王年之甲子,才完善了中国历史上的干支纪年法。我们只是想,依太初、三统历当年威信,东汉追正时,倒极有可能把地支十二周期的“子”关联天干地支六十周期“丙子”。战国时期的岁星纪年法,一岁行一星次,方便实用,一度深入人心。人们渐渐发现其不足,陆续追加种种弥补观念,产生虚拟概念太岁。《汉书∙天文志》称太岁,《淮南子·天文训》叫太阴,《史记∙天官书》叫岁阴。太岁的历史演变,众说纷纭。入汉以后到新莽时期,与史实纪年不合的岁星纪年法、太岁纪年法和岁阳、岁阳纪年法混用,各执一端,到汉章帝元和二年(85)东汉四分历的颁行,宣告正式结束 [13] 。我们只能说,“数从丙子起,算尽之外,则太岁日也”十四字中,除非有衍文夺字,否则,把太岁日与丙子相扯,实在是无奈之举。
6. 结论
整数对辗转相除序列现象的固有逻辑,指引着我们收集相关史料,一步步追根寻源。公元前7年,刘歆以古传岁星12岁11见,导出岁星会合周期。相约之后,以密近简化调出岁星岁数。独创岁星超辰纪年,编《世经》“以说《春秋》”。刘歆的推算,不乏刻意挂靠“乾坤之策”,人为修改数据,以特殊推一般,但应用密近简化,确凿无疑。根据紧随的四分历、乾象历、景初历,明确刘歆用过相约算法,并无不妥。在袁向东、李文林推测基础上,我们进一步推测,刘歆寻找反算31个元的数值解法,刺激上元积年概念的诞生,应该不是毫无依据的。涉及到落下闳,我们能做的,只是把吕子方推测中的连分数,换成等价的密近简化。再要想往远古探索,也只有依靠算理的内在凝聚力了。华罗庚人造行星数例,使我们认识到日行一度、天度圈的实践意义和理论意义。正是天度圈圈数之比蕴含的巨大潜力,刺激出密近简化,更刺激出求解满去式。终于,我们可以有把握地说,上元积年的本原,就是尧舜时的“岁三百有六旬有六日”。
中华文明,悠悠五千年。我们深深缅怀落下闳,这位力挽狂澜、功不可没,又急流勇退的民间天文学家。我们更深深缅怀一代代不知名的畴人子弟,积累历数,传播文明。正是他们,在人类文明史上,写下了浓重的一笔。
基金项目
江苏高校优势学科建设工程资助项目。
文章引用
王翼勋. 上元积年本原探索
On the Origin of the Shangyuan Jinian Period-Since-Grand-Epoch[J]. 自然科学, 2017, 05(01): 42-54. http://dx.doi.org/10.12677/OJNS.2017.51007
参考文献 (References)
- 1. 中华书局编辑部. 历代天文律历等志汇编•汉书•律历志[M]. 北京: 中华书局, 1976: 1419-1426
- 2. 中华书局编辑部. 历代天文律历等志汇编•汉书•律历志[M]. 北京: 中华书局, 1976: 1510-1513.
- 3. 中华书局编辑部. 历代天文律历等志汇编•晋书•律历志[M]. 北京: 中华书局, 1976: 1634-1644.
- 4. 华罗庚. 从祖冲之的圆周率谈起[M]. 北京: 人民教育出版社, 1962.
- 5. 吕子方. 中国科学技术史论文集上[M]. 中国科学院成都分院自然辩证法研究室吕子方遗著整理研究组整理, 成都: 四川人民出版社, 1983.
- 6. 秦九韶. 数书九章[M]. 郭书春, 编. 中国科学技术典籍通汇•数学卷第1册. 郑州: 河南教育出版社, 1993: 439-645.
- 7. 闵嗣鹤, 严士健. 初等数论[M]. 高等教育出版社, 第三版, 2003: 10.
- 8. 王翼勋. 两千年前的密近简化计算[J]. 数学传播, 2015, 39(2): 61-74.
- 9. 张培瑜, 陈美东, 薄树人, 胡铁珠. 中国古代历法[M]. 科学技术出版社, 2008: 250-300.
- 10. 袁向东, 李文林. 论汉历上元积年计算[M]. 科学史文集第3册, 上海: 上海科技出版社, 70-76.
- 11. Gauss, K.F. (1801) Disquistiones Arithmeticae. Gerh Fleischer, Lib-siae.
- 12. 王翼勋. 传统数学的千年等数和乘率之谜[J]. 数学传播, 2012, 36(4): 69-82.
- 13. 斯琴毕力格, 罗见今. 太初历的纪年问题——太岁纪年法被淘汰的原因[J]. 科学技术哲学研究, 2012, 29(1): 62- 69.
