基于加权马尔可夫模型的径流预测研究 Application of Weighted Markov Chain Model to Predict Runoff

doi:10.12677/JWRR.2012.16075

设为首页加入收藏期刊导航网站地图

期刊菜单

文章导航

Journal of Water Resources Research 水资源研究, 2012, 1, 470-474

http://dx.doi.org/10.12677/jwrr.2012.16075 Published Online December 2012 (http://www.hanspub.org/journal/jwrr.html)

Application of Weighted Markov Chain Model to Predict

Runoff*

Zhongling Hu, Bing Shen#, Jiqian g Lv

Key Laboratory of Northwest Water Resources and Environment Ecology, Xi’an University of Technology, Xi’an

Email: lingzi902@126.com, #shenbing@xaut.edu.cn

Received: Aug. 14th, 2012; revised: Aug. 29th, 2012; accepted: Sep. 7th, 2012

Abstract: This paper tries to take the Fuzzy C-Means method (FCM) to classify runoff state of Markov chain

model. Then aiming at the runoff characteristics of dependent random variables and taking order of autocor-

relation coefficients as the weights, Markov chain model is used to predict the following year runoff state.

The runoff state from 2001-2004 are predict based on the 54 years annual runoff data from 1950-2004 at Ji-

mai gauging station located in Dari country, Qinghai Province, the results are consistent with the actual situa-

tion. That means the application of Markov chain model with FCM to determine runoff state of Jimai gauging

station is feasible and effective.

Keywords: FCM; Weighted Markov Chain; Autocorrelation Coefficient; Annual Runoff

基于加权马尔可夫模型的径流预测研究*

胡忠玲，沈冰#，吕继强

西安理工大学西北水资源与环境生态教育部重点实验室，西安

Email: lingzi902@126.com, #shenbing@xaut.edu.cn

收稿日期：2012 年8月14 日；修回日期：2012 年8月29日；录用日期：2012年9月7日

摘要：本文尝试应用模糊 C均值聚类(FCM)划分马尔可夫链模型的径流状态区间，再针对径流量随

机变量特点，以各阶自相关系数为状态权重，应用该加权马尔可夫链模型预测径流量状态。依据青海

省达日县吉迈水文站 55 年(1950~2004)年径流量资料，预测了 2001~2004 年的径流状态，预测结果均

与实际情况相符合。说明用FCM 确定状态区间的马尔可夫链模型对吉迈水文站的径流状态预测是可

行的、有效的。

关键词：FCM；加权马尔可夫；自相关系数；年径流

1. 引言

径流预测在区域水资源规划中发挥着重要作用。

基于径流过程不确定性、不精确性的特点，用改进的

马尔可夫模型预测径流取得了较好的成果。由于马尔

可夫模型预测方法必须先将实数区间划分成有限个明

确的状态，然而在径流序列中状态并不是明确的子集

合，而是模糊状态，故用模糊子集来表示才更近似于

实际[1]。同时，在实际工作应用中，仅预测出未来某

时段径流量的适当的变化区间即可以完全满足精度要

求，这样预测的范围扩大了(由点值到区间)，其预测

的可靠性也可以相应地提高[2]。鉴于上述讨论，本文

提出了用模糊 C均值聚类(FCM)的方法划分状态及区

*基金项目：国家自然科学基金(No.50939004)。

#通讯作者。

作者简介：胡忠玲(1988-)，女，陕西榆林人，在读硕士生，从事水

文及水资源。

470

胡忠玲，等：基于加权马尔可夫模型的径流预测研究

第1卷 · 第6期

间，然后以径流序列规范化后的各阶自相关系数为权，

用该加权马尔可夫链来预测径流量的变化情况。

2. 理论与方法

2.1. 模糊C均值聚类(Fuzzy C-Means,

FCM)[3,4]

模糊 C均值聚类(FCM)，即众所周知的模糊

ISODATA，是用隶属度确定每个数据点属于某个聚类

的程度的一种聚类算法，其思想就是使得被划分到同

一簇的对象之间相似度最大，而不同簇之间的相似度

最小。

算法的输出是 C个聚类中心点向量和 C*N 的一

个模糊划分矩阵，这个矩阵表示的是每个样本点属于

每个类的隶属度。根据这个划分矩阵按照模糊集合中

的最大隶属原则就能够确定每个样本点归为哪个类。

聚类中心表示的是每个类的平均特征，可以认为是这

个类的代表点。

模糊 C均值聚类的具体原理及详细推导过程可见

参考文献[3,4]。

本文用 Matlab 提供的 FCM函数对径流序列数据

聚类，只需要输入一个初始变量，即序列所分的类数

C，就可以很快得出结果。

2.2. 马尔可夫链及加权马尔可夫链预测的思想

2.2.1. 马尔可夫链

马尔可夫过程是研究事物的状态及状态转移规

律的理论。它是通过对不同状态的初始概率及状态之

间的转移概率关系，来确定状态的变化趋势，从而达

到预测未来的目的[5]。时间和状态都离散的马尔科夫

过程，一般称马尔科夫链[6]。马尔科夫链的基本特点

是“马氏性”，也称“无后效性”，即在已知某一随机

过程“现在”的状态下，其“将来”的状态与“过去”

的状态是无关的。

2.2.2. 加权马尔可夫链预测的思想

加权马尔可夫链[5,7]的基本思想是：若水文序列满

“马氏性”及“各态历经性”，则对于这样一个相足

依的随机变量序列，其各阶自相关系数刻画了马尔科

夫过程的相关结构，因而可以根据该自相关结构，由

其前面若干时段的径流量状态对未来时段的径流量

状态进行加权预测，即：





i

P (1)

各阶自相关系数所占权重：



 (2)

则所要预测的时刻的状态j应满足：

 



max im

P P (3)

式中，m是预测时需要计算到的最大步长，其大小由

预报的精度要求来选择，1 ≤ k ≤ m；为序列的自相

关系数；为各初始年对应的状态i经过k步转变

到未来状态j的转移概率。加权的优点在于可以充分、

合理的利用已知信息进行预测，使预测结果更为准

确。



3. 实例分析

本文选取了青海省达日县吉迈水文站的 1950~

2004 年(其中 1950~1958 年的资料插值得到)的年径流

资料为例，用该加权马尔可夫链模型进行分析预测，

来说明该方法的具体应用并检验其预测效果。

本次研究先以1950~2000 年共 51 年的年径流序

列预测 2001 年的径流状态，然后将 2001 年实测资料

加入序列中，再预测 2002 年的径流状态，依此类推

预测 2003 年、2004 年的径流状态。

3.1. 确定马尔可夫链的状态空间

应用 Matlab 工具箱中的 FCM函数对 1950-2000

年径流序列进行模糊聚类，返回径流序列的聚类中心

和最后的隶属矩阵，根据隶属度划分状态。将径流划

分为四个状态，FCM 函数中的参数C取为 4，聚类结

果见模糊划分矩阵及各年所属状态如表 1。

输出的模糊划分矩阵

0.0712 0.1096 0.81580.0090 0.0730 0.0178

0.91370.8705 0.16580.9856 0.2989 0.9769

0.0122 0.01590.01410.0045 0.5869 0.0043

0.0030 0.00400.00430.0009 0.0412 0.0010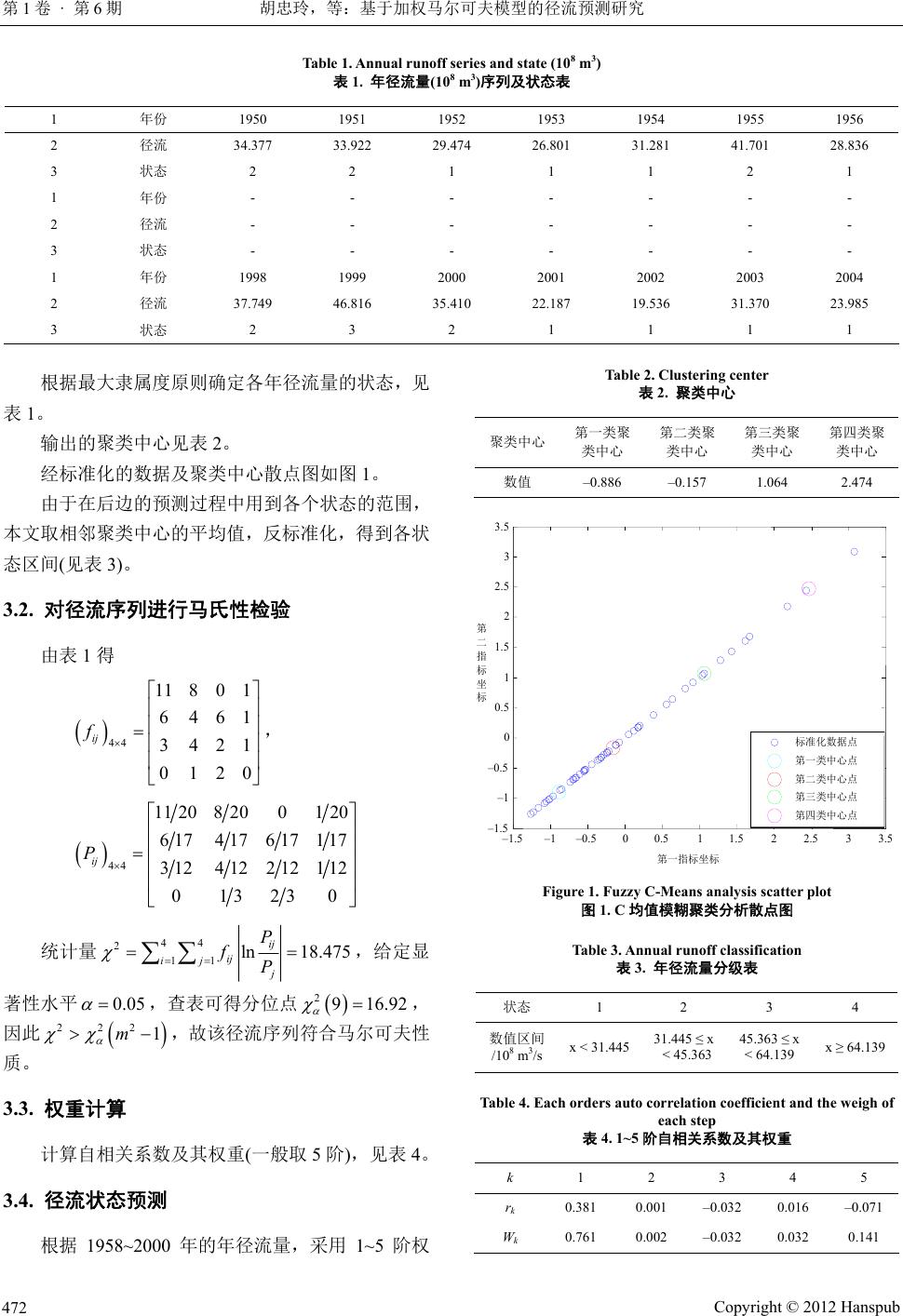













胡忠玲，等：基于加权马尔可夫模型的径流预测研究

第1卷 · 第6期

Table 1. Annual runoff series and state (108 m3)

表1. 年径流量(108 m3)序列及状态表

1 年份 1950 1951 1952 1953 1954 1955 1956

2 径流 34.377 33.922 29.474 26.801 31.281 41.701 28.836

3 状态 2 2 1 1 1 2 1

1 年份 - - - - - - -

2 径流 - - - - - - -

3 状态 - - - - - - -

1 年份 1998 1999 2000 2001 2002 2003 2004

2 径流 37.749 46.816 35.410 22.187 19.536 31.370 23.985

3 状态 2 3 2 1 1 1 1

根据最大隶属度原则确定各年径流量的状态，见

表1。

输出的聚类中心见表 2。

经标准化的数据及聚类中心散点图如图 1。

由于在后边的预测过程中用到各个状态的范围，

本文取相邻聚类中心的平均值，反标准化，得到各状

态区间(见表 3)。

3.2. 对径流序列进行马氏性检验

由表 1得



11 801

6461

3421

0120

f











，



11 208200120

617417617 117

3124 122 12112

013230

P













统计量 44

ln 18.475





 ，给定显

著性水平 0.05







222







，查表可得分位点，

因此，故该径流序列符合马尔可夫性

质。



29 16.92









1

3.3. 权重计算

计算自相关系数及其权重(一般取5阶)，见表 4。

3.4. 径流状态预测

根据 1958~2000 年的年径流量，采用 1~5 阶权

Table 2. Clustering center

表2. 聚类中心

聚类中心第一类聚

类中心

第二类聚

类中心

第三类聚

类中心

第四类聚

类中心

数值 –0.886 –0.157 1.064 2.474

–

1.5

–

0.5 00.5 1

1.5

2.533.5

–

1.5

–

0.5

1.5

2.5

3.5

第一指标坐标

标准化数据点

第一类中心点

第二类中心点

第三类中心点

第四类中心点

第

二

指

标

坐

标

Figure 1. Fuzzy C-Means analysis scatter plot

图1. C均值模糊聚类分析散点图

Table 3. Annual runoff classification

表3. 年径流量分级表

状态 1 2 3 4

数值区间

/108 m3/s x < 31.44531.445 ≤ x

< 45.363

45.363 ≤ x

< 64.139 x ≥ 64.139

Table 4. Each orders auto correlation coefficient and the weigh of

each step

表4. 1~5阶自相关系数及其权重

k 1 2 3 4 5

rk 0.381 0.001 –0.032 0.016 –0.071

Wk 0.761 0.002 –0.032 0.032 0.141

472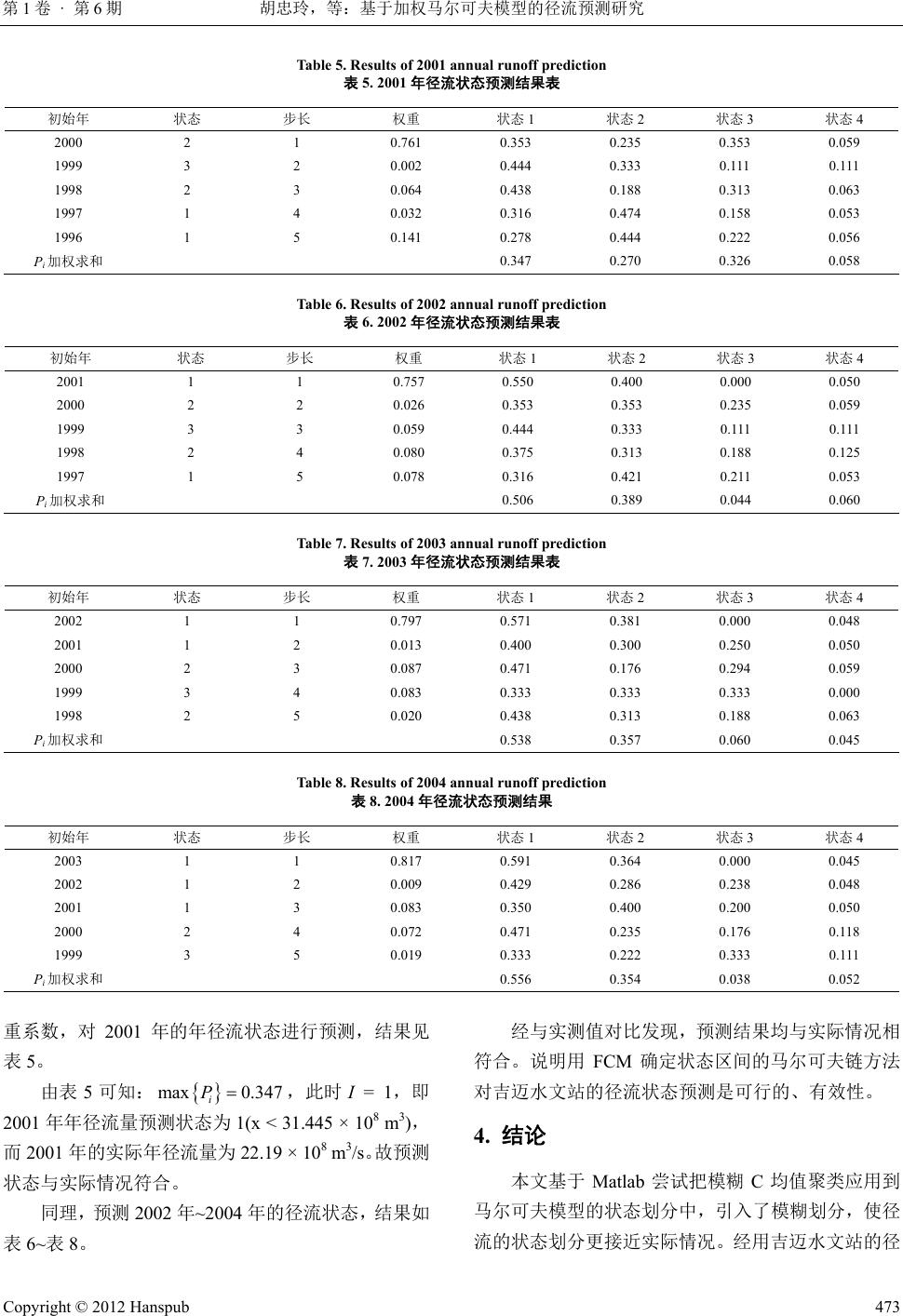

胡忠玲，等：基于加权马尔可夫模型的径流预测研究

第1卷 · 第6期

Table 5. Results of 2001 annual runoff prediction

表5. 2001年径流状态预测结果表

初始年状态步长权重状态 1 状态 2 状态 3 状态4

2000 2 1 0.761 0.353 0.235 0.353 0.059

1999 3 2 0.002 0.444 0.333 0.111 0.111

1998 2 3 0.064 0.438 0.188 0.313 0.063

1997 1 4 0.032 0.316 0.474 0.158 0.053

1996 1 5 0.141 0.278 0.444 0.222 0.056

Pi加权求和 0.347 0.270 0.326 0.058

Table 6. Results of 2002 annual runoff prediction

表6. 2002年径流状态预测结果表

初始年状态步长权重状态 1 状态 2 状态 3 状态 4

2001 1 1 0.757 0.550 0.400 0.000 0.050

2000 2 2 0.026 0.353 0.353 0.235 0.059

1999 3 3 0.059 0.444 0.333 0.111 0.111

1998 2 4 0.080 0.375 0.313 0.188 0.125

1997 1 5 0.078 0.316 0.421 0.211 0.053

Pi加权求和 0.506 0.389 0.044 0.060

Table 7. Results of 2003 annual runoff prediction

表7. 2003年径流状态预测结果表

初始年状态步长权重状态 1 状态 2 状态 3 状态 4

2002 1 1 0.797 0.571 0.381 0.000 0.048

2001 1 2 0.013 0.400 0.300 0.250 0.050

2000 2 3 0.087 0.471 0.176 0.294 0.059

1999 3 4 0.083 0.333 0.333 0.333 0.000

1998 2 5 0.020 0.438 0.313 0.188 0.063

Pi加权求和 0.538 0.357 0.060 0.045

Table 8. Results of 2004 annual runoff prediction

表8. 2004年径流状态预测结果

初始年状态步长权重状态 1 状态 2 状态 3 状态 4

2003 1 1 0.817 0.591 0.364 0.000 0.045

2002 1 2 0.009 0.429 0.286 0.238 0.048

2001 1 3 0.083 0.350 0.400 0.200 0.050

2000 2 4 0.072 0.471 0.235 0.176 0.118

1999 3 5 0.019 0.333 0.222 0.333 0.111

Pi加权求和 0.556 0.354 0.038 0.052

重系数，对 2001 年的年径流状态进行预测，结果见

表5。

由表 5可知：，此时 I = 1，即

2001 年年径流量预测状态为1(x < 31.445 × 108 m3)，

而2001 年的实际年径流量为 22.19 × 108 m3/s。故预测

状态与实际情况符合。



max 0.347

P

同理，预测2002 年~2004 年的径流状态，结果如

表6~表8。

经与实测值对比发现，预测结果均与实际情况相

符合。说明用 FCM 确定状态区间的马尔可夫链方法

对吉迈水文站的径流状态预测是可行的、有效性。

4. 结论

本文基于 Matlab 尝试把模糊C均值聚类应用到

马尔可夫模型的状态划分中，引入了模糊划分，使径

流的状态划分更接近实际情况。经用吉迈水文站的径

胡忠玲，等：基于加权马尔可夫模型的径流预测研究

第1卷 · 第6期

流资料检验是可行的、有效的。

参考文献 (References)

[1] 张琛. 一种改进的模糊马尔可夫链预测模型与应用研究[D].

辽宁工程技术大学, 2007.

ZHANG Chen. Research on forecast model and application of

an improved fuzzy Markov chain. Liaoning Technical University,

2007. (in Chinese)

[2] 孙才志, 张戈, 林学钰. 加权马尔可夫模型在降水丰枯状况

预测中的应用[J]. 系统工程理论与实践, 2003, 4: 100-105.

SUN Caizhi, ZHANG Ge and LIN Xueyu. Model of Markov

chain with weights and its application in predicting the precipi-

tation state. Systems Engineering-Theory & Practice, 2003, 4:

100-105. (in Chinese)

[3] 蔡静颖. 模糊 C均值算法的研究[D]. 辽宁师范大学, 2010.

CAI Jingyin. The research on fuzzy C-Means algorithm. Liao-

ning Normal University, 2010. (in Chinese)

[4] 梁静国, 张亚光, 戈华. CRM中的模糊C均值(FCM)客户聚

类算法研究[J]. 哈尔滨工程大学学报, 2004, 25(4): 257-260.

LIANG Jingguo, ZHANG Yaguang and GE Hua. Research on

fuzzy C-Means customer clustering algorithm (FCM) in CRM.

Journal of Harbin Engineering University, 2004, 25(4): 257-260.

(in Chinese)

[5] 王涛, 钱会, 李培月. 加权马尔可夫链在银川地区降雨量预

测中的应用[J]. 南水北调与水利科技, 2010, 8(1): 78-81.

WANG Tao, QIAN Hui and LI Peiyue. Prediction of precipita-

tion based on the weighted Markov chain in Yinchuan Area.

South-to-North Water Transfers and Water Science & Technology,

2010, 8(1): 78-81. (in Chinese)

[6] 王文圣, 丁晶. 随机水文学[M]. 中国水利水电出版社, 2008.

WANG Wensheng, DING Jin. Stochastic hydrology. China Na-

tional Water Resources and Hydropower Press, 2008. (in Chi-

nese)

[7] 刘德地, 陈晓宏. 一种北江流域年降雨量的权马尔可夫链预

测模型[J]. 水文, 2006, 26(6): 23-26.

LIU Dedi, CHEN Xiaohong. Annual precipitation forecasting

based on the weighted Markov chain in Beijiang River basin.

Journal of China Hydrology, 2006, 26(6): 23-26. (in Chinese)

474