 Modern Physics 现代物理, 2012, 2, 88-93 http://dx.doi.org/10.12677/mp.2012.24015 Published Online November 2012 (http://www.hanspub.org/journal/mp.html) Properties of Paraelectric Phase KTa0.5Nb0.5O3 Surface Researched by First-Principles Hongguo Sun, Xiaoniu Yang Polymer Composites Engineering Laboratory, Changchun Institute of Applied Chemistry, Chinese Academy of Sciences, Changchun Email: sunhongguo@ciac.jl.cn Received: Sep. 18th, 2012; revised: Oct. 4th, 2012; accepted: Oct. 19th, 2012 Abstract: Potassium tantalite niobate, KTa0.5Nb0.5O3 (KTN) has paraelectric and ferroelectric properties. The properties of crystal surfaces are studied with first-principles based on the Density Functional Theory (DFT). Geometrical struc- ture optimization, band structure, and density of states (DOS) of KTN (100) surface are calculated and analyzed. The dielectric functions of KTN (100), (110) and (111) surfaces, which can calculate all other optical properties of the mate- rial such as reflectivity, refractive index, conductivity, absorption, and energy loss function, etc. are evaluated. Compare the results with bulk, there are essential difference between interior and surface, which are according with theoretical predictions. Keywords: First-Principles; KTN; Surface; Band Structure; Density of States 顺电相 KTa0.5Nb0.5O3晶体表面性质的第一性原理研究 孙洪国,杨小牛 中国科学院长春应用化学研究所高分子复合材料工程实验室,长春 Email: sunhongguo@ciac.jl.cn 收稿日期:2012 年9月18 日;修回日期:2012年10 月4日;录用日期:2012 年10月19 日 摘 要:运用基于密度泛函理论第一性原理的局域密度近似法对具有铁电压电性能的钽铌酸钾 KTa0.5Nb0.5O3晶 体(100)表面进行几何结构优化,并进一步计算能带和态密度。计算得到的不同晶向表面介电函数,其它光学性 质常数如反射率、折射率、传导率和能量损失函数等都可由介电函数通过计算得到。将计算结果与对应体块材 料相应参数进行比较分析。结果显示表面的各种性能与体块材料存在本质的不同,与理论预期一致。 关键词:第一性原理;钽铌酸钾;表面;能带;态密度 1. 引言 KTN 晶体作为无铅铁电材料,具有较大的二次电 光效应,同时半波电压小,是具有重大发展前景的光 电信息功能材料[1-3]。对其开展理论研究具有重要的指 导意义和应用价值,对 KTN 晶体及其衍生物的深入 研究是未来信息科学发展的重要方向[4,5]。KTaO3是量 子顺电体,与其它各种钙钛矿型氧化物具有良好的晶 格匹配和结构匹配。KNbO3是典型铁电体,KNbO3 与BaTiO3晶体一样,随着温度降低会依次发生从立方 相(m3m)到四方相(4mm)到正交相(mm2)再到三角相 (3m)的相变,高温立方相为顺电相,其余三个为铁电 相,居里温度为708 K。Nb 和Ta 在原子周期表中属 于同族,具有比较相似的物理化学性质。因此,KTaO3 和KNbO3非常容易以任意比例组成 KTaxNb1−xO3固溶 体。其中,B位阳离子在晶体内部呈无序状态分布。 顺电相 KTN 超晶胞是具有典型钙钛矿结构的氧 八面体,每一个Ta 原子或 Nb 原子都基本处于钾立方 和氧八面体的中心[6]。正氧八面体有3个四重轴、4 Copyright © 2012 Hanspub 88  顺电相 KTa0.5Nb0.5O3晶体表面性质的第一性原理研究 个三重轴和 6个两重轴,含氧八面体铁电的自发极化 主要来源于 B位阳离子偏离八面体中心的运动,B位 阳离子偏离中心的位移通常是沿着这 3个高对称方向 之一[7]。针对 KTN 体块材料的计算已有较多相应的讨 论,但对其表面性能计算相关报道较少,有必要对其 展开第一性原理计算和研究。 2. 计算方法和 KTN 晶体表面模型的建立 计算采用密度泛函理论方法(第一性原理计算方 法)。最早有关铁电材料的第一性原理计算的报道出现 在1990 年,是Cohen 对钙钛矿型 BaTiO3的结构和晶 格动力学方面的研究[8]。在材料结构和性能计算的相 关领域,第一性原理计算方法有着极高的计算精度, 能够十分准确地计算和预估许多凝聚态物质中的性 质[9]。例如晶体与薄膜材料的能带结构和态密度等性 质[10]、半导体相关特性、铁电与反铁电性质、磁性质 和光学性质[11,12]等。另外,对于材料表面结构和物性, 掺杂和缺陷分析,以及近期发展速度较快的纳米碳管 和其他纳米材料的物性分析,也都是一种十分优秀的 方法[13-16]。 建立 KTN 晶体[100]晶向的模型,以氧八面体的 形式绘出。其中,铌原子,和钽原子平均占据八面体 中心,氧占据八面体的各顶点。进一步利用 Build Vacuum Slab Crystal工具得到 KTN[100]晶向加入真空 层后形成的(100)表面理论模型,如图 1所示。 将晶格参数初始值设定为(a,b,c) = (4.000 Å, 4.000 Å,4.000 Å),α,β,γ均为 90˚。在建立KTN 表面模型时,对真空层的厚度值选取为 10.000 Å,经 计算验证,加入这个真空层厚度对于表面计算是较适 合的,能有效解决晶体模型中表面边界条件的问题。 从图 1中可以看出,超晶胞结构相当于沿着 KNbO3 原胞[100]晶向堆放一个 KTaO3原胞,然后加入真空层 形成表面模型。将 Nb 和Ta 有序排列在晶格内部, Figure 1. Theory model of KTN supercell (100) surface 图1. KTN超晶胞表面(100)表面理论模型 计算有序排列超晶胞结构性质,并可以将其计算结果 推广至 KTN 固溶体。在初始KTN 超晶胞中,每一个 Ta 原子或Nb 原子都基本处于钾立方体和氧八面体的 中心,这说明原始 KTa0.5Nb0.5O3超晶胞和表面模型是 顺电相。 3. 计算结果和讨论 3.1. 顺电相 KTN晶体(100)表面几何结构优化 对超晶胞模型(100)表面进行几何结构优化。 K(3s2, 3p6, 4s1),Ta (5d3, 6s2),Nb(4d4, 5s1)和O(2s2, 2p4) 被认为是价态电子,计算其它条件设置如下:最大平 面波截止能为380 eV,结构优化总能收敛精度为10–7 eV/atom,原子受力收敛至0.02 eV/Å,计算结果均通 过平面波截止能量收敛测试,表面模型的 k点选取为 6 × 3 × 2。经过优化得到稳定结构且符合周期性边界 条件,并通过收敛测试。 经测试实验制备的块状 KTa0.67Nb0.33O3材料的晶 格常数为(3.993 Å,3.993 Å,7.986 Å)[17]。计算得到的 KTa0.5Nb0.5O3超晶胞 2 × 2 × 2 结构的体块材料晶格常 数为(4.001 Å,4.001 Å,7.982 Å)[18]。我们计算得到 KTN 晶体(100)表面的晶格常数分别为3.966 Å,3.965 Å和19.993 Å,在 a,b方向与块状材料实验值较接 近,说明计算结果具有可信性。但计算结果都相对偏 小,说明表面与体块的结构存在差别。另外,在加入 真空层的c方向,处于表面的晶胞晶格常数相对于材 料内部增加了0.03 Å,真空层的厚度相对初始设置值 增加了 1.961 Å,都发生了明显的变化。这说明在真 空层方向原子由于处于表面受到的束缚相对于晶体 内部较小,更易与外部环境相互作用;另外,也与软 件中采用的近似方法对晶格起到的压缩性束缚等诸 多因素相关。 3.2. 能带结构与态密度计算结果 在布里渊区沿着对称线方向绘出 KTN(100)表面 能带结构图。图 2给出了能带的两个区域:从0 eV 到5.0 eV 处于导带区域;从–5.0 eV 到0 eV 处于价带 区域。可以验证具有BO6结构的氧八面体对导带底部 和价带顶部起重要支配作用,这些相关能带主要是来 自B位钽和铌离子d轨道和氧离子 2p轨道的贡献[19]。 由于存在轨道杂化和共价键的形成,钽铌离子的电荷 Copyright © 2012 Hanspub 89 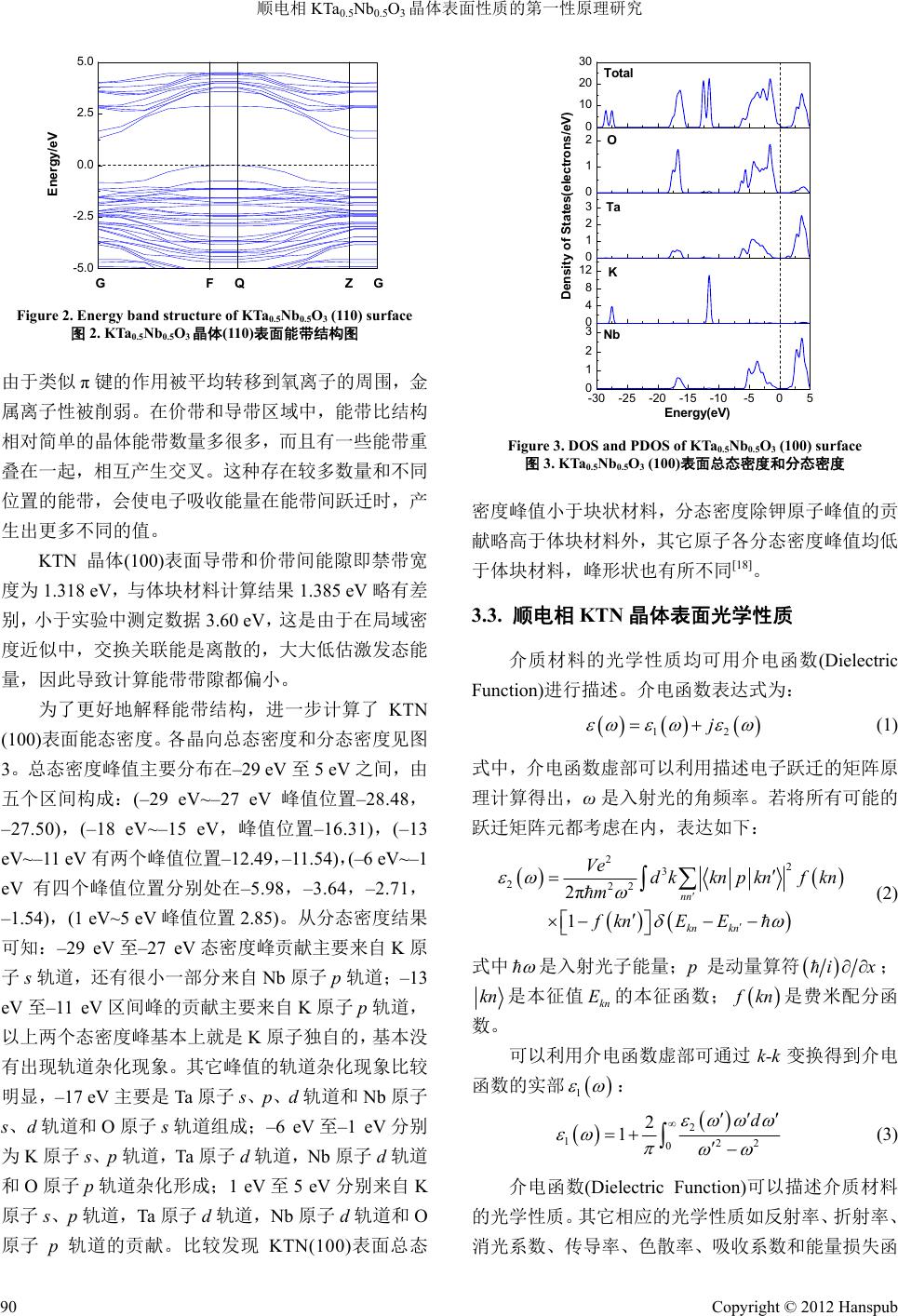 顺电相 KTa0.5Nb0.5O3晶体表面性质的第一性原理研究 -5.0 -2.5 0.0 2.5 5.0 Energy/eV G F Q Z G Figure 2. Energy band structure of KTa0.5Nb0.5O3 (110) surface 图2. KTa0.5Nb0.5O3晶体(110)表面能带结构图 由于类似π键的作用被平均转移到氧离子的周围,金 属离子性被削弱。在价带和导带区域中,能带比结构 相对简单的晶体能带数量多很多,而且有一些能带重 叠在一起,相互产生交叉。这种存在较多数量和不同 位置的能带,会使电子吸收能量在能带间跃迁时,产 生出更多不同的值。 KTN 晶体(100)表面导带和价带间能隙即禁带宽 度为 1.318 eV,与体块材料计算结果1.385 eV 略有差 别,小于实验中测定数据 3.60 eV,这是由于在局域密 度近似中,交换关联能是离散的,大大低估激发态能 量,因此导致计算能带带隙都偏小。 为了更好地解释能带结构,进一步计算了KTN (100)表面能态密度。各晶向总态密度和分态密度见图 3。总态密度峰值主要分布在–29 eV 至5 eV 之间,由 五个区间构成:(–29 eV~–27 eV峰值位置–28.48, –27.50),(–18 eV~–15 eV,峰值位置–16.31),(–13 eV~–11 eV 有两个峰值位置–12.49,–11.54),(–6 eV~–1 eV 有四个峰值位置分别处在–5.98,–3.64,–2.71, –1.54),(1 eV~5 eV 峰值位置2.85)。从分态密度结果 可知:–29 eV至–27 eV态密度峰贡献主要来自 K原 子s轨道,还有很小一部分来自 Nb 原子p轨道;–13 eV 至–11 eV区间峰的贡献主要来自 K原子 p轨道, 以上两个态密度峰基本上就是K原子独自的,基本没 有出现轨道杂化现象。其它峰值的轨道杂化现象比较 明显,–17 eV 主要是Ta 原子 s、p、d轨道和Nb 原子 s、d轨道和 O原子 s轨道组成;–6 eV至–1 eV分别 为K原子 s、p轨道,Ta原子 d轨道,Nb 原子 d轨道 和O原子 p轨道杂化形成;1 eV至5 eV分别来自 K 原子 s、p轨道,Ta 原子d轨道,Nb 原子 d轨道和O 原子 p轨道的贡献。比较发现 KTN(100)表面总态 -30-25-20-15-10 -505 0 1 2 3 0 4 8 12 0 1 2 3 0 1 2 0 10 20 30 Energy(eV) Nb K Ta O Density of States(electrons/eV) Total Figure 3. DOS and PDOS of KTa0.5Nb0.5O3 (100) surface 图3. KTa0.5Nb0.5O3 (100)表面总态密度和分态密度 密度峰值小于块状材料,分态密度除钾原子峰值的贡 献略高于体块材料外,其它原子各分态密度峰值均低 于体块材料,峰形状也有所不同[18]。 3.3. 顺电相 KTN晶体表面光学性质 介质材料的光学性质均可用介电函数(Dielectric Function)进行描述。介电函数表达式为: 12 j (1) 式中,介电函数虚部可以利用描述电子跃迁的矩阵原 理计算得出,ω是入射光的角频率。若将所有可能的 跃迁矩阵元都考虑在内,表达如下: 22 3 222 2π 1 nn kn kn Ve dkknpknf kn m fknE E (2) 式中 是入射光子能量;p是动量算符 ix ; kn 是本征值 的本征函数; kn E f kn 是费米配分函 数。 可以利用介电函数虚部可通过k-k 变换得到介电 函数的实部 1 : 2 122 0 2 1d (3) 介电函数(Dielectric Function)可以描述介质材料 的光学性质。其它相应的光学性质如反射率、折射率、 消光系数、传导率、色散率、吸收系数和能量损失函 Copyright © 2012 Hanspub 90 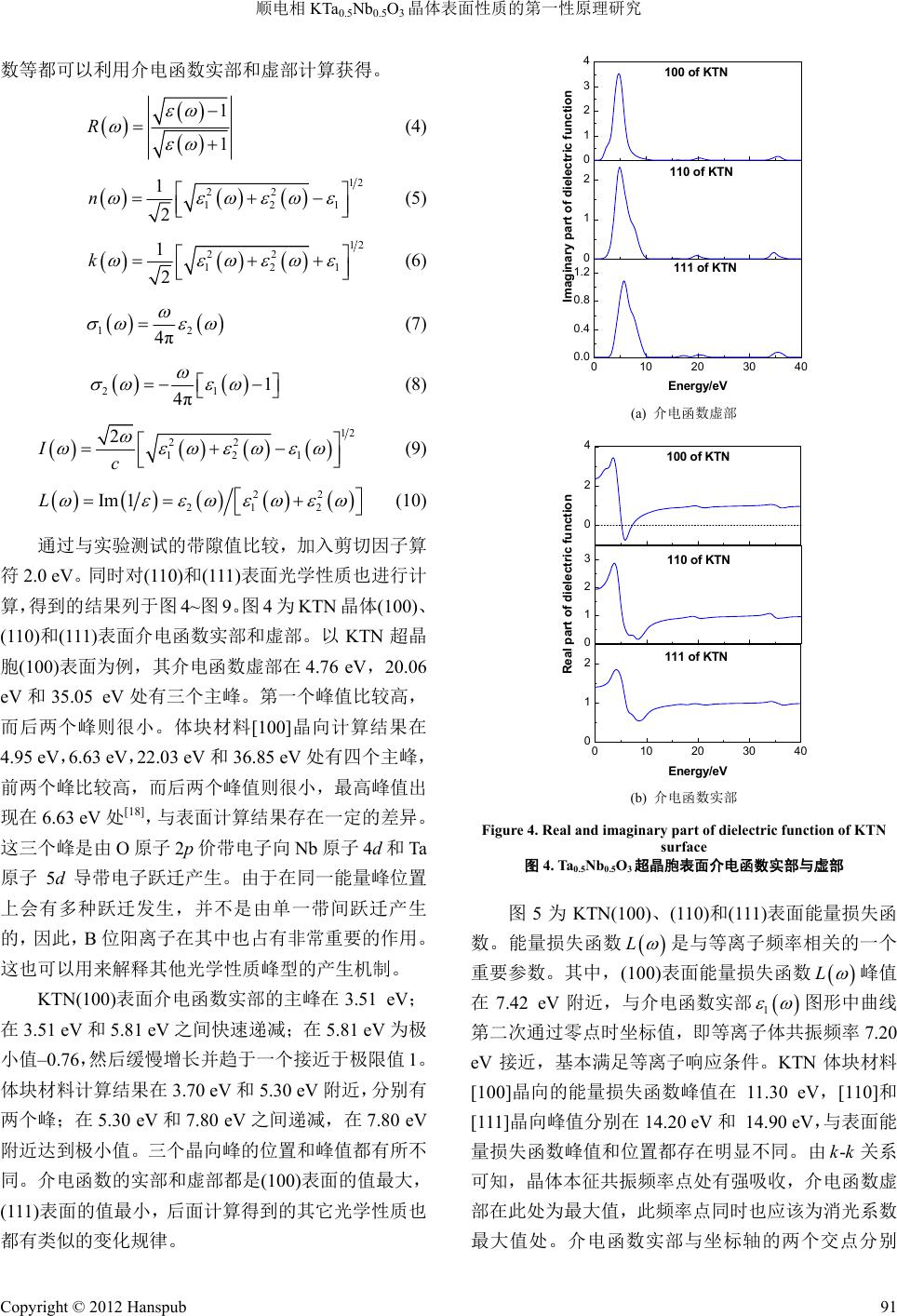 顺电相 KTa0.5Nb0.5O3晶体表面性质的第一性原理研究 数等都可以利用介电函数实部和虚部计算获得。 1 1 R (4) 12 22 121 1 2 n (5) 12 22 121 1 2 k (6) 12 4π (7) 21 1 4π (8) 12 22 121 2 Ic (9) 22 21 2 Im 1L (10) 通过与实验测试的带隙值比较,加入剪切因子算 符2.0 eV。同 时 对(110)和(111)表面光学性质也进行计 算,得到的结果列于图 4~图9。图 4为KTN晶体(100)、 (110)和(111)表面介电函数实部和虚部。以 KTN 超晶 胞(100)表面为例,其介电函数虚部在 4.76 eV,20.06 eV 和35.05 eV处有三个主峰。第一个峰值比较高, 而后两个峰则很小。体块材料[100]晶向计算结果在 4.95 eV,6.63 eV,22.03 eV 和36.85 eV 处有四个主峰, 前两个峰比较高,而后两个峰值则很小,最高峰值出 现在 6.63 eV处[18],与表面计算结果存在一定的差异。 这三个峰是由 O原子2p价带电子向 Nb原子 4d和Ta 原子 5d导带电子跃迁产生。由于在同一能量峰位置 上会有多种跃迁发生,并不是由单一带间跃迁产生 的,因此, B位阳离子在其中也占有非常重要的作用。 这也可以用来解释其他光学性质峰型的产生机制。 KTN(100)表面介电函数实部的主峰在3.51 eV; 在3.51 eV 和5.81 eV 之间快速递减;在5.81 eV 为极 小值–0.76,然后缓慢增长并趋于一个接近于极限值 1。 体块材料计算结果在 3.70 eV 和5.30 eV 附近,分别有 两个峰;在 5.30 eV和7.80 eV之间递减,在 7.80 eV 附近达到极小值。三个晶向峰的位置和峰值都有所不 同。介电函数的实部和虚部都是(100)表面的值最大, (111)表面的值最小,后面计算得到的其它光学性质也 都有类似的变化规律。 0 1 2 3 4 0 1 2 0 1020304 0.0 0.4 0.8 1.2 0 100 of KTN 110 of KTN Imaginary part of dielectric function 111 of KTN Energy/eV (a) 介电函数虚部 0 2 4 0 1 2 3 0 1020304 0 1 2 0 100 of KTN 110 of KTN Real part of dielectric function 111 of KTN Energy/eV (b) 介电函数实部 Figure 4. Real and imaginary part of dielectric function of KTN surface 图4. Ta0.5Nb0.5O3超晶胞表面介电函数实部与虚部 图5为KTN(100)、(110)和(111)表面能量损失函 数。能量损失函数 L 是与等离子频率相关的一个 重要参数。其中,(100)表面能量损失函数 L 峰值 在7.42 eV附近,与介电函数实部 1 图形中曲线 第二次通过零点时坐标值,即等离子体共振频率 7.20 eV 接近,基本满足等离子响应条件。KTN 体块材料 [100]晶向的能量损失函数峰值在 11.30 eV,[110]和 [111]晶向峰值分别在 14.20 eV和 14.90 eV,与表面能 量损失函数峰值和位置都存在明显不同。由 关系 可知,晶体本征共振频率点处有强吸收,介电函数虚 部在此处为最大值,此频率点同时也应该为消光系数 最大值处。介电函数实部与坐标轴的两个交点分别 -kk Copyright © 2012 Hanspub 91  顺电相 KTa0.5Nb0.5O3晶体表面性质的第一性原理研究 0 1020304 0.0 0.5 1.0 0 0 1 2 3 0 1 2 111 of KTN 100 of KTN Energy/eV 110 of KTN Loss Function Figure 5. Energy loss function of KTa0.5Nb0.5O3 surface 图5. KTa0.5Nb0.5O3超晶胞表面能量损失函数 接近本征共振频率 0 和等离子体共振频率 p ;在介 电函数虚部曲率变化最大处,介电函数实部出现峰值 和谷值。同时计算了 KTN 表面的其它光学性质,计 算结果如图 6~图9所示。 KTN 晶体(100)表面吸收系数的计算结果如图 9 所示。将其与实验制备的四方相 KTa0.6Nb0.4O3纳米颗 粒紫外波段测试结果进行比较,与材料制备所用氢氧 化钾浓度为 17 mol/L 时最为接近,但仍然有一倍多的 差距[20],与其它制备条件下的相比相差更多,这进一 步说明表面与材料内部之间性质的不同。 晶体表面结构存在不饱和键和范德瓦尔斯力,表 面原子对轨道电子束缚能力与体块材料相比,电子更 容易吸收能量之后逃逸,相对活性也大于体块材料, 另外原子外层电子轨道杂化作用也与块状材料不同。 各表面的各项光学性质与块状材料相同晶向相比,也 有所不同。由于各种相关性质均由介电函数计算得 到,因此,都存在着与介电函数实部与虚部类似的变 化。与块状材料相应晶向对比,也都存在相应的差异。 在此不再一一详述。 4. 结论 通过第一性原理计算了顺电相KTN 超晶胞(100) 表面几何结构、能带结构和电子态密度,计算了不同 晶向表面的介电函数、能量损失函数、折射率、反射 率等光学性质。由态密度计算可以看出,各原子在不 同情况下对几何优化结果和光学性质的贡献,与体块 0 1020304 0.00 0.02 0.04 0.06 0 0.00 0.04 0.08 0.12 0.0 0.1 0.2 0.3 0.4 111 of KTN Energy/eV 110 of KTN Reflectivity 100 of KTN Figure 6. Reflectivity of KTa0.5Nb0.5O3 surfaces 图6. KTa0.5Nb0.5O3超晶胞表面反射率 0.0 0.5 1.0 1.5 2.0 0.0 0.5 1.0 1.5 2.0 0 1020304 0.4 0.8 1.2 1.6 0 100 of KTN 110 of KTN Refractive index 111 of KTN Energy/eV Figure 7. Refractive index of KTN surface 图7. KTa0.5Nb0.5O3超晶胞表面折射率 0 1020304 0.0 0.2 0.4 0 0.0 0.4 0.8 0.0 0.5 1.0 1.5 111 of KTN Energy/eV 110 of KTN Conductivity 100 of KTN Figure 8. Real part of conductivity of KTN surface 图8. KTa0.5Nb0.5O3超晶胞表面传导率 Copyright © 2012 Hanspub 92 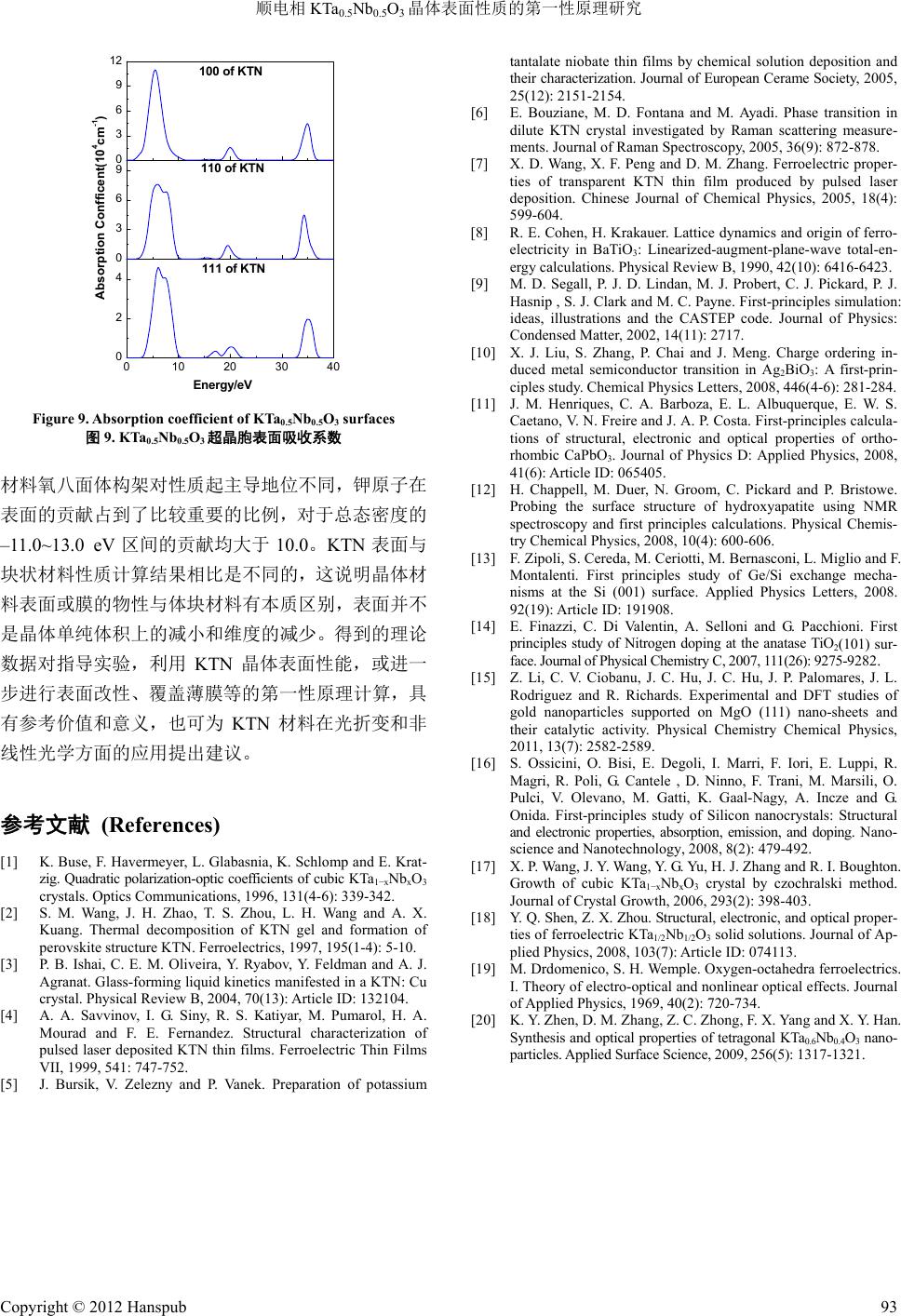 顺电相 KTa0.5Nb0.5O3晶体表面性质的第一性原理研究 Copyright © 2012 Hanspub 93 0 3 6 9 0 1020304 0 2 4 0 0 3 6 9 12 110 of KTN Energy/eV 111 of KTN Absorption Confficent(104cm-1) 100 of KTN Figure 9. Absorption coefficient of KTa0.5Nb0.5O3 surfaces 图9. KTa0.5Nb0.5O3超晶胞表面吸收系数 材料氧八面体构架对性质起主导地位不同,钾原子在 表面的贡献占到了比较重要的比例,对于总态密度的 –11.0~13.0 eV区间的贡献均大于 10.0。KTN 表面与 块状材料性质计算结果相比是不同的,这说明晶体材 料表面或膜的物性与体块材料有本质区别,表面并不 是晶体单纯体积上的减小和维度的减少。得到的理论 数据对指导实验,利用 KTN晶体表面性能,或进一 步进行表面改性、覆盖薄膜等的第一性原理计算,具 有参考价值和意义,也可为 KTN材料在光折变和非 线性光学方面的应用提出建议。 参考文献 (References) [1] K. Buse, F. Havermeyer, L. Glabasnia, K. Schlomp and E. Krat- zig. Quadratic polarization-optic coefficients of cubic KTa1−xNbxO3 crystals. Optics Communications, 1996, 131(4-6): 339-342. [2] S. M. Wang, J. H. Zhao, T. S. Zhou, L. H. Wang and A. X. Kuang. Thermal decomposition of KTN gel and formation of perovskite structure KTN. Ferroelectrics, 1997, 195(1-4): 5-10. [3] P. B. Ishai, C. E. M. Oliveira, Y. Ryabov, Y. Feldman and A. J. Agranat. Glass-forming liquid kinetics manifested in a KTN: Cu crystal. Physical Review B, 2004, 70(13): Article ID: 132104. [4] A. A. Savvinov, I. G. Siny, R. S. Katiyar, M. Pumarol, H. A. Mourad and F. E. Fernandez. Structural characterization of pulsed laser deposited KTN thin films. Ferroelectric Thin Films VII, 1999, 541: 747-752. [5] J. Bursik, V. Zelezny and P. Vanek. Preparation of potassium tantalate niobate thin films by chemical solution deposition and their characterization. Journal of European Cerame Society, 2005, 25(12): 2151-2154. [6] E. Bouziane, M. D. Fontana and M. Ayadi. Phase transition in dilute KTN crystal investigated by Raman scattering measure- ments. Journal of Raman Spectroscopy, 2005, 36(9): 872-878. [7] X. D. Wang, X. F. Peng and D. M. Zhang. Ferroelectric proper- ties of transparent KTN thin film produced by pulsed laser deposition. Chinese Journal of Chemical Physics, 2005, 18(4): 599-604. [8] R. E. Cohen, H. Krakauer. Lattice dynamics and origin of ferro- electricity in BaTiO3: Linearized-augment-plane-wave total-en- ergy calculations. Physical Review B, 1990, 42(10): 6416-6423. [9] M. D. Segall, P. J. D. Lindan, M. J. Probert, C. J. Pickard, P. J. Hasnip , S. J. Clark and M. C. Payne. First-principles simulation: ideas, illustrations and the CASTEP code. Journal of Physics: Condensed Matter, 2002, 14(11): 2717. [10] X. J. Liu, S. Zhang, P. Chai and J. Meng. Charge ordering in- duced metal semiconductor transition in Ag2BiO3: A first-prin- ciples study. Chemical Physics Letters, 2008, 446(4-6): 281-284. [11] J. M. Henriques, C. A. Barboza, E. L. Albuquerque, E. W. S. Caetano, V. N. Freire and J. A. P. Costa. First-principles calcula- tions of structural, electronic and optical properties of ortho- rhombic CaPbO3. Journal of Physics D: Applied Physics, 2008, 41(6): Article ID: 065405. [12] H. Chappell, M. Duer, N. Groom, C. Pickard and P. Bristowe. Probing the surface structure of hydroxyapatite using NMR spectroscopy and first principles calculations. Physical Chemis- try Chemical Physics, 2008, 10(4): 600-606. [13] F. Zipoli, S. Cereda, M. Ceriotti, M. Bernasconi, L. Miglio and F. Montalenti. First principles study of Ge/Si exchange mecha- nisms at the Si (001) surface. Applied Physics Letters, 2008. 92(19): Article ID: 191908. [14] E. Finazzi, C. Di Valentin, A. Selloni and G. Pacchioni. First principles study of Nitrogen doping at the anatase TiO2(101) sur- face. Journal of Physical Chemistry C, 2007, 111(26): 9275-9282. [15] Z. Li, C. V. Ciobanu, J. C. Hu, J. C. Hu, J. P. Palomares, J. L. Rodriguez and R. Richards. Experimental and DFT studies of gold nanoparticles supported on MgO (111) nano-sheets and their catalytic activity. Physical Chemistry Chemical Physics, 2011, 13(7): 2582-2589. [16] S. Ossicini, O. Bisi, E. Degoli, I. Marri, F. Iori, E. Luppi, R. Magri, R. Poli, G. Cantele , D. Ninno, F. Trani, M. Marsili, O. Pulci, V. Olevano, M. Gatti, K. Gaal-Nagy, A. Incze and G. Onida. First-principles study of Silicon nanocrystals: Structural and electronic properties, absorption, emission, and doping. Nano- science and Nanotechnology, 2008, 8(2): 479-492. [17] X. P. Wang, J. Y. Wang, Y. G. Yu, H. J. Zhang and R. I. Boughton. Growth of cubic KTa1−xNbxO3 crystal by czochralski method. Journal of Crystal Growth, 2006, 293(2): 398-403. [18] Y. Q. Shen, Z. X. Zhou. Structural, electronic, and optical proper- ties of ferroelectric KTa1/2Nb1/2O3 solid solutions. Journal of Ap- plied Physics, 2008, 103(7): Article ID: 074113. [19] M. Drdomenico, S. H. Wemple. Oxygen-octahedra ferroelectrics. I. Theory of electro-optical and nonlinear optical effects. Journal of Applied Physics, 1969, 40(2): 720-734. [20] K. Y. Zhen, D. M. Zhang, Z. C. Zhong, F. X. Yang and X. Y. Han. Synthesis and optical properties of tetragonal KTa0.6Nb0.4O3 nano- particles. Applied Surface Science, 2009, 256(5): 1317-1321. |