Modeling and Simulation
Vol.
13
No.
02
(
2024
), Article ID:
83588
,
11
pages
10.12677/mos.2024.132166
基于数据驱动场景建模的综合能源系统调度 方法
申江兰1,毛业涛1,聂祥论1,王志杨2*,李义1
1贵州电网有限责任公司毕节供电局,贵州 毕节
2贵州大学电气工程学院,贵州 贵阳
收稿日期:2024年2月2日;录用日期:2024年3月21日;发布日期:2024年3月29日

摘要
在“双碳”目标的大背景下,耦合了多种异质能源的综合能源系统(Integrated Energy Systems, IES)在可再生能源消纳、能源梯级利用等方面具拥有巨大优势。然而,可再生能源–负荷需求的双侧不确定性对IES的优化调度方法提出了巨大的挑战。针对该问题,本文提出了一种基于数据驱动场景建模的IES日前优化调度方法。在海量功率数据的基础上,建立了基于变分自编码器(Variational Auto-Encoder, VAE)的IES源–荷场景生成模型,并通过改进的K-means聚类算法进行场景削减,得到精确的典型运行场景。随后,建立了以运行成本期望最低为目标函数的IES日前场景随机优化调度模型,有效提升了IES的运行经济性,为不确定性条件下的IES调度提供了理论指导。
关键词
综合能源系统,变分自编码器,优化调度,随机优化,风电场

Data-Driven Scenario Generation-Based Optimal Scheduling Method for Integrated Energy Systems
Jianglan Shen1, Yetao Mao1, Xianglun Nie1, Zhiyang Wang2*, Yi Li1
1Bijie Power Supply Bureau of Guizhou Power Grid Co., Ltd., Bijie Guizhou
2College of Electrical Engineering, Guizhou University, Guiyang Guizhou
Received: Feb. 2nd, 2024; accepted: Mar. 21st, 2024; published: Mar. 29th, 2024

ABSTRACT
Integrated Energy Systems (IES) coupled with diverse energy sources offer significant advantages in both renewable energy consumption and energy gradient utilization within the context of the “double carbon” target. Nevertheless, the dual-sided uncertainty in renewable energy-load demand significantly affects the optimization methodology of IES scheduling. To tackle this issue, the paper introduces a data-driven optimal scheduling method for IES, based on scenario generation. Utilizing extensive power data, an IES source-load scenario generation model using Variational Auto-Encoder (VAE) is developed, followed by scenario reduction through an enhanced K-means clustering algorithm, enabling the extraction of precise typical operating scenarios. Consequently, a stochastic optimal scheduling model is formulated for IES day-ahead scenarios, aiming to minimize operating costs, thereby enhancing the operational economy of IES, and offering theoretical guidance for scheduling under uncertain conditions.
Keywords:Integrated Energy System, Variational Self-Coder, Optimal Scheduling, Stochastic Optimization, Wind Farms

Copyright © 2024 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
环境污染问题日益严重,传统能源系统中不同类型的能量网络相互独立运行,加大了能源的浪费,阻碍了我国“双碳”目标的实现 [1] 。开展可再生能源开发与利用、建设多能源耦合系统势在必行。对此,IES承担起了多种能源的运输、转换、储存和消费的主要物理载体,为多能源的协同互补运行提供了新的解决方案 [2] 。然而,新能源渗透率增加与能源需求多样化存在大量不确定性因素,使IES安全经济运行面临挑战 [3] 。
发电侧可再生能源出力的波动和用户侧负荷需求的波动是IES中不确定性的主要来源,这些波动往往受到多种因素的影响,而IES的运行计划又与源–荷功率场景密切相关 [4] 。因此,如何刻画源–荷双侧波动情况,实现不确定环境下IES的最优运行就是提升能源利用效率的核心问题。鲁棒优化(Robust Optimization, RO)和随机优化(Stochastic Optimization, SO)方法是常用的不确定建模方法。然而,RO着重考虑在最劣运行条件下找到可行解,可能导致最终求解的运行方案过于保守 [5] 。与其相比,SO的经济性更佳,且能更好处理多重不确定因素下的优化问题。
基于运行场景的SO是较为有效的建模方法。场景生成是其核心,场景集精度决定了最终优化的结果 [6] 。传统场景生成方法依靠概率模型与数学统计模型实现,主要方法包括正态分布、马尔可夫链 [7] 、Copula模型 [8] 等。文献 [9] 采用蒙特卡洛抽样生成可再生能源出力场景,通过多时间尺度模型对IES进行调度,但其对不确定变量特征的刻画过于简单。文献 [10] 采用拉丁超立方采样与Cholesky分解生成运行场景,但仅考虑了风电波动,不够贴近真实情况。实际源–荷功率不确定性往往包含大量复杂因素,选择何种概率分布模型对其进行刻画尚未有定论,而模型参数更是难以确定,使得该方法在处理多不确定因素的场景生成问题上处于劣势 [11] 。
近年来,有学者提出了基于数据驱动的场景建模方法。该方法不依赖具体数学模型,仅通过学习大量历史数据中的场景分布,生成新的运行场景样本,大大降低了复杂场景生成问题的复杂度 [12] 。文献 [13] 提出了一种基于生成对抗网络(Generative Adversarial Network, GAN)的负荷场景生成方法并证明了其生成精度,但GAN自身网络结构复杂、训练困难和梯度消失等问题,使其难以应用于实际。文献 [14] 提出了一种基于条件变分自编码器(Variational Auto-Encoder, VAE)的风光场景生成方法,可高质量的生成指定条件下的风光出力场景。然而,其仅刻画源侧的不确定性,而未能同时考虑源–荷双侧的不确定变量并生成对应源–荷运行场景,可能难以满足未来IES中能源高效利用与经济运行的需求。
为解决上述问题,本文提出了一种基于数据驱动场景建模的IES日前优化调度方法。通过建立基于VAE的IES源–荷场景生成模型,提取并抽象源–荷场景数据中的高维隐含信息,生成大量负荷实际的源–荷场景;采用改进的K-means算法对生成场景进行快速削减,得到IES典型源–荷出力场景。在此基础上,构建以运行成本期望最低为目标函数的IES调度模型,求解得到不确定环境下IES的最优调度运行计划。最后,通过算例分析说明了本文所提方法的优势。
2 数据驱动的源-荷场景建模方法
2.1. VAE网络模型介绍
VAE是一种在自编码器基础上演变而来的数据生成式神经网络。VAE是以变分推断理论为基础,从概率的角度描述隐含层数据空间,其出色的特征提取能力使其近年来被广泛应用于各种数据生成领域 [15] ,其大致结构如下图1:
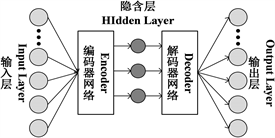
Figure 1. The general structure of the VAE
图1. VAE的大致结构
VAE中包含两个主要的网络模型:一个用于对输入数据X进行变分推理,生成潜变量Z的变分概率分布推理,称为编码器;另一个用于还原变分推理数据,其根据潜变量Z的变分概率分布重构原始数据的近似概率分布,称为解码器。设输入数据x与潜变量z之间存在一定的映射关系,则其可通过联合概率密度分布函数 进行描述。因此,VAE的训练损失函数L则为原始概率分布 与后验概率分布 之间的KL散度最小:
(1)
使用条件条件概率密度函数将式(1)中的联合概率密度函数进行替换得:
(2)
式中: 为常数项,将第二项提取并整理得到损失函数:
(3)
式中:第一项主要表示生成样本与真实样本之间的差异,称之为重构误差损失;第二项主要表示为编码网络拟合的隐变量后验概率分布 与先验分布 之间的KL散度。
2.2. 基于VAE的IES源–荷场景生成方法
VAE通过编码–解码的方式可抽象学习到数据中的深层次耦合关系与隐含逻辑。由于IES中的不确定性主要来源于电网,包括电源侧风电功率波动与负荷侧电负荷需求的波动。因此,本文采用VAE作为IES中源–荷场景生成的核心模型,具体包括以下三个阶段:数据处理阶段、网络训练阶段、场景生成阶段(图2)。
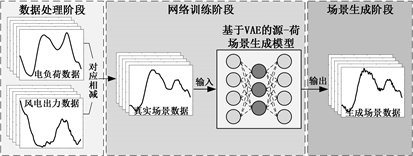
Figure 2. The VAE-based method for source-load scenarios generation
图2. 基于VAE的源–荷场景生成方法
在数据处理阶段:为了能够同时提取风电功率数据与电负荷数据之间时序性、相关性特征,本文将IES源–荷运行场景描述为单一功率缺额的形式。首先匹配同日的风电、电负荷数据,然后用对应时刻的电负荷减去风电出力,形成单一功率缺额的IES源–荷场景序列数据。
在网络训练阶段:以全连接层构建VAE网络,序列输入输出层的大小设置为24,将源–荷场景序列数据输入网络进行训练,提取数据高维抽象特征信息,通过Adam算法更新网络权重,不断迭代训练直到网络损失收敛至给定值。
在场景生成阶段:多次输入日前预测的源–荷场景数据,使VAE网络生成大量的IES源–荷运行场景,为后续场景削减提供充足样本。
2.3. 基于改进K-means算法的源–荷场景削减方法
K-means聚类算法是一种简单高效的无监督数据聚类算法,核心思想是根据样本的相似度将样本划分成不同的子集 [16] 。对任意场景集合 ,该算法通过完全随机的方式选择初始聚类质心,然后不断迭代直到满足式(4)的方式将其数据划分至K个的聚类子集中:
(4)
式中: 表示为场景
与质心
之间的欧式距离最小值。
表示为场景
与质心
之间的欧式距离最小值。
虽然K-means算法可快速筛选出典型场景,但其收敛速度和聚类效果受初始聚类中心的影响极大,完全随机的生成初始聚类中心可能会使多数聚类中心出现在同一聚类簇中,此时将难以收敛至最小值,导致选择出的典型场景不够精准。因此,本文对K-means算法在初始聚类中心的选取方面做出改进,具体如下:
1) 在场景集合数据中以均匀分布的方式选取一个点,作为初始聚类中心 ;
2) 计算集合内各样本点至当前已有聚类中心的欧式距离 ,选取概率 的最大值点作为新的聚类中心 ;
3) 重复执行步骤2,直至完成全部K个聚类中心的选取。
该改进的核心是增加K-means算法初始聚类中心的差异性,避免迭代过程中陷入局部最优值,将算法的搜索域扩大至全集合空间,从而实现更加精准的生成场景削减。
3. IES日前优化调度模型
3.1. IES整体结构与主要设备数学模型
本文以一个包含电、热、气三能量网络互联耦合运行的IES为研究对象,该IES通过协调多异质能源网络之间互补运行,提升了整体的用能效率。关键设备的能量转化关系介绍如下图3:
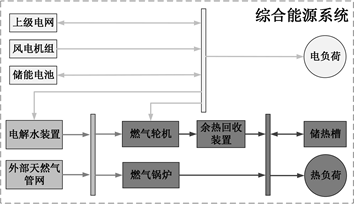
Figure 3. The overall structure of the IES model
图3. IES模型整体结构
1) 燃气轮机–余热回收装置:
燃气轮机通过天然气燃烧后的高温蒸汽推动涡轮机叶片做功,将动能转化为电能:
(5)
式中: 和 分别为燃气轮机t时刻的电功率和天然气耗量; 为燃气轮机转化率; 为天然气燃烧系数;m为功率与热值换算率。
余热回收装置主要用于将燃气轮机在工作过程中产生的大量废热回收再利用:
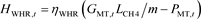 (6)
(6)
式中: 为余热回收装置t时刻输出的热功率; 为余热回收装置的热能回收效率。
2) 燃气锅炉:
燃气锅炉通过燃烧天然气发热:
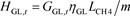 (7)
(7)
式中: 和 分别为燃气锅炉t时刻输出热功率和消耗天然气量; 为燃气锅炉的热效率。
3) 电转气(Power-to-Gas, P2G)装置:
P2G装置可实现电能至天然气的转化:
(8)
式中: 和 分别为P2G装置t时刻输出天然气量和消耗电功率; 为P2G的转换率。
3.2. IES日前优化调度的目标函数
在VAE生成IES源–荷出力场景基础上,本文构建了基于场景SO的IES日前优化调度模型,通过将不确定问题转化为基于场景的确定性问题求解,实现IES的高效经济运行 [17] 。IES的优化目标函数为期望运行成本最小,具体为:
(9)
(10)
式中:
、
、
、
、
、
和
分别为燃气轮机、储能电池、P2G装置、储热槽、燃气锅炉、外部天然气管网和上级电网的运行成本。S为场景总数量;
为场景s的概率。
、
、
、
和
分别为燃气轮机、储能电池、P2G装置、储热槽和燃气锅炉的运行成本系数。IES可与上级电网进行功率交换, 和
分别为t时刻向上级电网的购电价格和售电价格;
和
分别为场景s下t时刻IES向上级电网的购电和售电功率。
为t时刻的天然气购气价格;
为场景s下t时刻IES的天然气的购气量。
和
分别为t时刻向上级电网的购电价格和售电价格;
和
分别为场景s下t时刻IES向上级电网的购电和售电功率。
为t时刻的天然气购气价格;
为场景s下t时刻IES的天然气的购气量。
3.3. IES日前优化调度的约束条件
1) 能量平衡约束:
(11)
(12)
(13)
式中:
和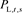 为表示场景s下t时刻风电机组的输出电功率和电负荷需求。
为场景s下t时刻的热负荷需求。
为表示场景s下t时刻风电机组的输出电功率和电负荷需求。
为场景s下t时刻的热负荷需求。
2) 设备运行约束:
(14)
式中: 为设备i在场景s下t时刻的输出; 和 分别为设备i的最小和最大输出限制; 和 分别为设备i输出的下爬坡、上爬坡限制。
3) 储能约束设备约束:
(15)
式中, 和 分别为储能i在场景s下t时刻的0~1运行状态变量; 和 分别为储能i在场景s下t时刻的充能和放能功率; 为储能i的最大运行功率限制; 为储能i的能量转换效率; 为储能i在场景s下t时刻的内部储能水平; 和 分别为储能i的最小和最大储能水平; 和 分别为储能i的始末储能水平。
4 算例分析
4.1. 算例参数设置介绍
本文训练集数据来源于贵州省某地实测数据,共包含450日。算例基于Python3.6平台编译并调用求解器Cplex对调度模型进行求解。VAE训练设置100轮,学习率为0.0001。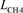 为9.7 kWh/m3,m为3.6;储能电池容量为500 kWh,初始容量50%,最大最小荷电状态分别为95%和10%;储热槽容量为300 kWh,初始容量50%,最大最小储热状态分别为90%和10%;电网与IES之间的最大功率限制为±600 kW,气网向IES输送天然气的限制为800 V3。购售电价采用分时电价,购气采用分时气价,具体如下表所示。
为9.7 kWh/m3,m为3.6;储能电池容量为500 kWh,初始容量50%,最大最小荷电状态分别为95%和10%;储热槽容量为300 kWh,初始容量50%,最大最小储热状态分别为90%和10%;电网与IES之间的最大功率限制为±600 kW,气网向IES输送天然气的限制为800 V3。购售电价采用分时电价,购气采用分时气价,具体如下表所示。
Table 1. Time-of-use tariff setting
表1. 分时电价设置
Table 2. Time-of-use gas price setting
表2. 分时气价设置
Table 3. IES device parameter settings
表3. IES设备参数设置
表1~3中参数为本文选取的示例系统参数,实际应用中虽然不同IES的参数不尽相同,导致模拟计算所得结果可能不同,但这并不影响本文方法所得结论的普适性,因此所得结论仍成立。
4.2. 源–荷场景生成有效性分析
本文采用VAE与改进K-means对IES的源–荷运行场景进行生成与削减,设置VAE生成场景数量为300,改进K-means场景缩减数量设置为4,所得结果如图4、图5所示:
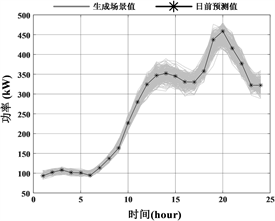
Figure 4. Data-driven VAE-based source-load scenario generation results
图4. 基于数据驱动VAE的源–荷场景生成结果
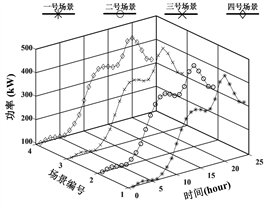
Figure 5. Source-load scenario reduction results based on improved K-means
图5. 基于改进K-means的源–荷场景削减结果
将本文所提方法与基于概率建模的传统场景生成方法进行对比。对于传统方法,通过正态分布刻画源–荷不确定变量波动情况,采用蒙特卡洛抽样进行场景生成,所得结果如下:

Figure 6. Generation results of source-load scenarios based on traditional probabilistic models
图6. 基于传统概率模型的源–荷场景生成结果
由图4和图6可知,基于本文方法所生成的场景曲线形态更加集中,均靠近于日前功率预测曲线附近,同时各场景曲线的变化幅度较为合理。与之相比,基于传统方法所生成的场景曲线更为分散,部分点存在功率的急剧变化,不符合实际。传统场景生成方法仅从概率密度函数的角度刻画并抽样生成源–荷场景,而未能考虑源–荷功率数据之间的相关性、时序性。本文所提VAE源–荷场景生成方法可通过编码–解码的方法从数据角度提取并抽象源–荷功率数据高维特征,从而更好的刻画源–荷功率波动情况。
4.3. IES日前优化调度有效性分析
在获得4类典型场景的基础上,通过基于场景的SO优化调度方法对所提IES进行日前优化调度,求解得到IES日前运行成本为10,882¥,所得调度运行计划如图7所示。
将本文调度方法与RO方法进行对比,不同调度方法下的运行成本见表4。
由表4可知,本文所提场景SO方法求解的IES日前运行计划经济性明显好于RO方法。这是由于RO方法重点考虑不确定变量处于最坏情况来进行优化调度,而却忽略了不确定变量仅在小概率范围内会到达波动范围边界的事实,从而导致调度方案过于保守且不太经济。相比RO,本文所提场景SO方法充分考虑到了不确定变量的可能波动范围与波动特征,并针对最可能出现的几种典型场景进行了优化调度。基于场景的SO方法可在保证可靠应对不确定变量波动的同时,提升系统的经济性。
5. 结论
本文针对源–荷不确定性的IES难以优化调度问题,提出了一种基于数据驱动场景生成的IES日前优化调度方法,所得结论如下:
1) IES通过多能耦合协同运行的方式,有效提升了可再生能源的消纳率,推进现代能源系统向绿色、低碳、高效的方向转型。
2) 基于数据驱动的VAE可有效模拟源–荷双侧不确定性变量波动特征,相比传统方法,可生成更加准确实际的源–荷场景。

Figure 7. Day-ahead optimized scheduling results of the IES
图7. IES日前优化调度结果图
Table 4. Cost comparison of different scheduling methods
表4. 不同调度方法的成本对比
3) 基于场景的SO调度模型可有效应对IES中的源–荷不确定性,在保证IES稳定运行的同时,提升系统运行的经济性。
文章引用
申江兰,毛业涛,聂祥论,王志杨,李 义. 基于数据驱动场景建模的综合能源系统调度方法
Data-Driven Scenario Generation-Based Optimal Scheduling Method for Integrated Energy Systems[J]. 建模与仿真, 2024, 13(02): 1759-1769. https://doi.org/10.12677/mos.2024.132166
参考文献
- 1. 杨龙, 张沈习, 程浩忠, 等. 区域低碳综合能源系统规划关键技术与挑战[J]. 电网技术, 2022, 46(9): 3290-3304.
- 2. 贾宏杰, 王丹, 徐宪东, 等. 区域综合能源系统若干问题研究[J]. 电力系统自动化, 2015, 39(7): 198-207.
- 3. 尚文强, 李广磊, 丁月明, 等. 考虑源荷不确定性和新能源消纳的综合能源系统协同调度方法[J/OL]. 电网技术: 1-17. https://kns.cnki.net/kcms2/article/abstract?v=2dRWw02s3kyQiFTmTPi7W9EEsTLOJBjMbgdV2l1QeOtqwdWecE_KLnfXky528MPPw4CjX375XLP8gXPKqAoYEb2uAjWbDe9akXlP-mNKP6BCOctIuqLT4ge4QFw3diE1ZhXY92NHsHY=&uniplatform=NZKPT&language=CHS, 2023-09-22.
- 4. 祁晓敏, 孔力, 熊煌, 等. 源荷储协调的冷热电综合能源系统随机优化运行[J]. 电工电能新技术, 2021, 40(3): 10-21.
- 5. 王旭强, 张鑫, 刘红昌, 等. 考虑源荷双重不确定性的电-气互联综合能源系统分布鲁棒优化调度[J] 现代电力, 2019, 36(6): 52-60.
- 6. 杜威, 刘东, 李文云, 等. 基于配网节点电价的综合能源系统随机优化[J]. 电力建设, 2020, 41(12): 139-149.
- 7. 董雷, 孟天骄, 陈乃仕, 等. 采用马尔可夫链—多场景技术的交直流主动配电网优化调度[J]. 电力系统自动化, 2018, 42(5): 147-153.
- 8. 汤向华, 李秋实, 侯丽钢, 等. 基于Copula函数的风电时序联合出力典型场景生成[J]. 电力工程技术, 2020, 39(5): 152-161 168.
- 9. 徐健玮, 马刚, 高丛, 等. 基于风光场景生成的综合能源系统日前-日内优化调度[J]. 分布式能源, 2022, 7(4): 18-27.
- 10. 王玲玲, 王昕, 郑益慧, 等. 计及多个风电机组出力相关性的配电网无功优化[J]. 电网技术, 2017, 41(11): 3463-3469.
- 11. 董骁翀. 基于数据驱动的可再生能源场景生成与约简方法研究[D]: [硕士学位论文]. 北京: 华北电力大学, 2020.
- 12. 王子馨. 基于机器学习的综合能源系统随机优化调度策略[D]: [硕士学位论文]. 北京: 华北电力大学, 2021.
- 13. 张宇帆, 艾芊, 李昭昱, 等. 基于生成对抗网络的负荷序列随机场景生成方法[J]. 供用电, 2019, 36(1): 29-33 92.
- 14. 王守相, 陈海文, 李小平, 等. 风电和光伏随机场景生成的条件变分自动编码器方法[J]. 电网技术, 2018, 42(6): 1860-1869.
- 15. 翟正利, 梁振明, 周炜, 等. 变分自编码器模型综述[J]. 计算机工程与应用, 2019, 55(3): 1-9.
- 16. Shao, H., Jiang, H., Lin, Y., et al. (2018) A Novel Method for Intelligent Fault Diagnosis of Rolling Bearings Using Ensemble Deep Auto-Encoders. Mechanical Systems and Signal Processing, 102, 278-297. https://doi.org/10.1016/j.ymssp.2017.09.026
- 17. 周丹, 孙可, 郑朝明, 等. 考虑供热系统热储能特性的电-热综合系统随机优化调度模型研究[J]. 可再生能源, 2020, 38(3): 380-387.
NOTES
*通讯作者。
