Pure Mathematics
Vol.06 No.03(2016), Article ID:17524,5
pages
10.12677/PM.2016.63026
Cores of Super Rpp Semigroups
Huoping Ye, Junying Guo, Xiaojiang Guo
College of Mathematics and Information, Jiangxi Normal University, Nanchang Jiangxi
Received: Apr. 25th, 2016; accepted: May 9th, 2016; published: May 12th, 2016
Copyright © 2016 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
In this note, central (overabelian) super rpp semigroup is defined. These semigroups are generalization of the related classes of completely regular semigroups in the range of super rpp semi- groups. Some characterizations of such semigroups are obtained.
Keywords:Super Rpp Semigroup, Completely 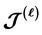 -Simple Semigroup
-Simple Semigroup

超Rpp半群的核心
叶火平,郭俊颖,郭小江
江西师范大学,数学与信息科学学院,江西 南昌

收稿日期:2016年4月25日;录用日期:2016年5月9日;发布日期:2016年5月12日

摘 要
本文定义了中心(扩交换)超rpp半群,这些半群是完全正则半群子类在超rpp半群中的推广。文中给出了中心(扩交换)超rpp半群的若干特征。
关键词 :超Rpp半群,完全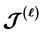 -单半群
-单半群

1. 引言和准备
半群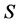 的核心
的核心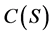 定义为它的所有幂等元生成的子半群。由于幂等元为半群结构的骨架,半群核心自然能够提供半群许多结构信息,因此研究半群的核心就非常有意义。本文将研究超rpp半群的核心。
定义为它的所有幂等元生成的子半群。由于幂等元为半群结构的骨架,半群核心自然能够提供半群许多结构信息,因此研究半群的核心就非常有意义。本文将研究超rpp半群的核心。
令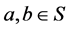 。定义
。定义
 当且仅当对于任意
当且仅当对于任意 ,
, 。
。
下面已知结果将多次用到(可见 [1] )。
引理1.1令 ,则
,则 当且仅当
当且仅当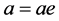 ,且对于任意的
,且对于任意的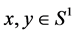 ,
,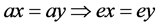 。
。
半群 称为rpp半群,如果对于任意的
称为rpp半群,如果对于任意的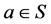 ,作为
,作为 -系
-系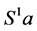 是投射的。等价地,
是投射的。等价地,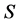 为rpp半群当且仅当每一个
为rpp半群当且仅当每一个 -类都含有幂等元。进一步,rpp半群
-类都含有幂等元。进一步,rpp半群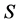 称为强rpp半群(strongly rpp semigroup),如果对于任意的
称为强rpp半群(strongly rpp semigroup),如果对于任意的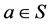 ,存在惟一的幂等元
,存在惟一的幂等元 使得
使得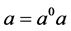 且
且 。强rpp半群
。强rpp半群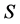 称为超rpp半群(super rpp semigroup),如果等价关系
称为超rpp半群(super rpp semigroup),如果等价关系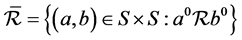 是左同余。
是左同余。
现令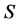 为强rpp半群。如 [2] ,定义
为强rpp半群。如 [2] ,定义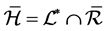 。显然,
。显然, 的每个
的每个 -类都含幂等元,并且是左消幺半群。众所周知,完全正则半群是超rpp半群,特别地,当
-类都含幂等元,并且是左消幺半群。众所周知,完全正则半群是超rpp半群,特别地,当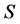 是完全正则半群时,
是完全正则半群时,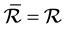 ,进而
,进而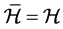 。事实上,超rpp半群是完全正则半群当且仅当它是正则的。
。事实上,超rpp半群是完全正则半群当且仅当它是正则的。
令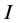 ,
,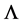 为非空集合,且
为非空集合,且 为左消幺半群。令
为左消幺半群。令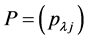 为
为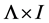 -矩阵,其元素均为
-矩阵,其元素均为 的单位。在集合
的单位。在集合 上,定义运算
上,定义运算
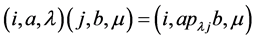 。
。
关于上面的运算,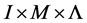 构成强rpp半群,称为
构成强rpp半群,称为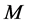 上关于夹心矩阵(sandwich matrix)
上关于夹心矩阵(sandwich matrix)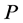 的Rees矩阵半群,并记为
的Rees矩阵半群,并记为 。我们称同构于某左消幺半群上的Rees矩阵半群的强rpp半群为完全
。我们称同构于某左消幺半群上的Rees矩阵半群的强rpp半群为完全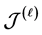 -单半群(关于完全
-单半群(关于完全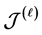 -单半群,参见 [3] [4] )。
-单半群,参见 [3] [4] )。
引理1.2 ( [2] [5] ) 令 为左消幺半群
为左消幺半群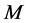 上关于夹心矩阵(sandwich matrix)
上关于夹心矩阵(sandwich matrix)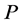 的Rees矩阵半群。则
的Rees矩阵半群。则
(1)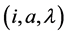 为幂等元当且仅当
为幂等元当且仅当 ;
;
(2) 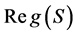 (
(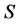 的所有正则元组成的集合)
的所有正则元组成的集合) ,且构成
,且构成 的子半群;
的子半群;
(3) ;
;
(4) 当且仅当
当且仅当 。
。
文 [2] 中,Guo-Guo-Shum指出:rpp半群为超rpp半群当且仅当它为一些完全 -单半群的半格。
-单半群的半格。
2. 主要结论
本文采用文献 [6] 中的概念和术语,为方便计,用叙述“令 为超rpp半群”表示“
为超rpp半群”表示“ 为超rpp半群,且
为超rpp半群,且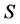 为完全
为完全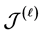 -单半群
-单半群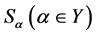 的半格”。
的半格”。
引理2.1 超rpp半群满足正则性条件(即,其正则元集构成子半群),从而超rpp半群的正则元构成完全正则子半群。
证明 令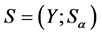 为超rpp半群。为证:
为超rpp半群。为证: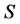 满足正则性条件,仅需证:
满足正则性条件,仅需证: 的幂等元乘积为正则元。为此,设
的幂等元乘积为正则元。为此,设 ,
, 分别为
分别为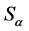 和
和 的幂等元,则
的幂等元,则 ,进而
,进而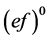 为
为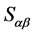 中的幂等元。注意到,
中的幂等元。注意到,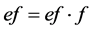 ,我们有
,我们有 ,以致于
,以致于 ,从而
,从而 为
为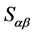 的幂等元。另一方面,不难知道,
的幂等元。另一方面,不难知道,
 ,于是
,于是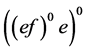 为
为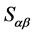 的幂等元。而
的幂等元。而 ,现在
,现在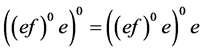 ,进而
,进而 ,这样
,这样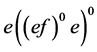 为
为 的幂等元。故
的幂等元。故 ,再据
,再据
引理1.2 (2), 为
为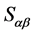 的正则元。这样,证明了:
的正则元。这样,证明了: 的幂等元的乘积为正则元。
的幂等元的乘积为正则元。
注意到,完全 -单半群的正则元组成完全单半群。不难知道,超rpp半群的正则元都是完全的,从而超rpp半群的正则元构成完全正则子半群。
-单半群的正则元组成完全单半群。不难知道,超rpp半群的正则元都是完全的,从而超rpp半群的正则元构成完全正则子半群。
基于引理2.1,再据( [7] , Proposition II. 6.2, p. 89),下面命题显然。
命题2.2 令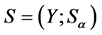 为超rpp半群,则
为超rpp半群,则
(1)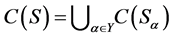 ;
;
(2) 对于任意的 (
(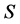 的幂等元集),
的幂等元集),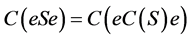 。
。
文 [7] 中,Petrich-Reilly研究了中心完全正则半群(central completely regular semigroup)。类似地,定义中心超rpp半群。
定义2.3超rpp半群 称为中心的(central),如果任意两个幂等元的乘积都包含在其所在的
称为中心的(central),如果任意两个幂等元的乘积都包含在其所在的 -类的中心内。
-类的中心内。
下面的命题给出了中心超rpp半群的一些性质,它推广了( [7] , Theorem II . 6.4, p. 90)。
命题2.4 令 为超rpp半群,则以下各款等价:
为超rpp半群,则以下各款等价:
(1) 是中心的;
是中心的;
(2) 对于任意的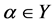 ,
,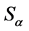 是中心的;
是中心的;
(3) 对于任意的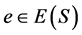 ,
, 包含在
包含在 的中心内,此处
的中心内,此处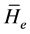 为包含幂等元
为包含幂等元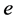 的
的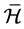 -类。
-类。
(4)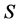 满足恒等式:
满足恒等式: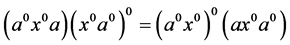 。
。
证明 据( [1] , Proposition6.9)的证明, ,进而
,进而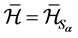 。再据定义2.3,不难知道,
。再据定义2.3,不难知道,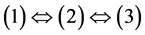 显然。
显然。
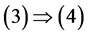 令
令 ,
, ,则
,则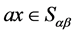 。由于
。由于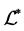 为右同余,有
为右同余,有
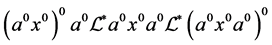 。
。
注意到,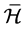 在正则元上恰为
在正则元上恰为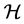 。再据引理2.1,有
。再据引理2.1,有 ,其中
,其中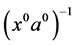 是
是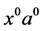 在
在 -类中的逆元。另外,据引理1.2,含幂等元
-类中的逆元。另外,据引理1.2,含幂等元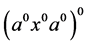 的
的 的
的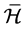 -类为
-类为 。从而
。从而
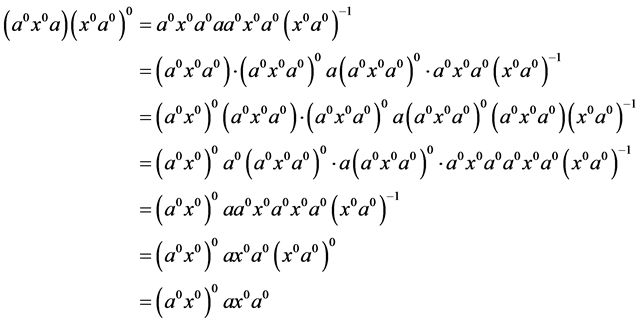
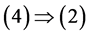 令
令 ,且
,且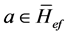 ,则
,则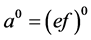 。据( [7] , Lemma II . 4.4, p. 75),知
。据( [7] , Lemma II . 4.4, p. 75),知
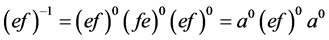 。注意到,
。注意到,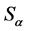 的所有正则元构成完全单半群。易知,
的所有正则元构成完全单半群。易知,
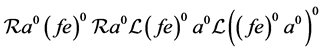 。从而
。从而
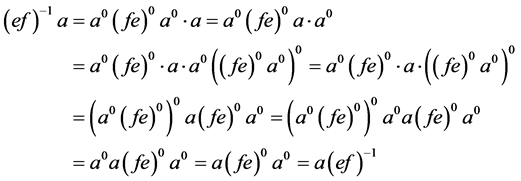 ,
,
进而
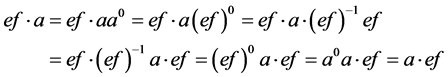 ,
,
于是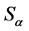 为中心的。
为中心的。
定义2.5 超rpp半群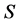 称为扩交换的(overabelian),如果
称为扩交换的(overabelian),如果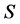 的每一个
的每一个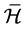 -类都是交换幺半群。
-类都是交换幺半群。
据定义,易知,扩交换超rpp半群是中心的。不难看出,扩交换超rpp半群是扩交换完全正则半群的推广。并且,扩交换超rpp半群为扩交换完全正则半群,当且仅当它是正则的。下面给出扩交换超rpp半群的一个特征。
命题2.6令 为超rpp半群,则
为超rpp半群,则 为扩交换的当且仅当
为扩交换的当且仅当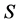 满足恒等式:
满足恒等式: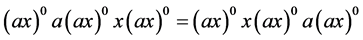 。
。
证明 设 为扩交换超rpp半群。令
为扩交换超rpp半群。令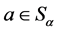 ,
,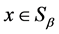 ,则
,则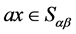 ,进而
,进而 ,再据引理1.2,
,再据引理1.2,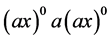 ,
,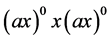 在同一个
在同一个 -类中,从而
-类中,从而
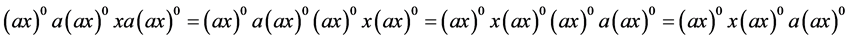 。
。
反之,设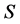 满足恒等式:
满足恒等式: 。对于任意两个属于同一
。对于任意两个属于同一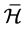 -类的元素
-类的元素 ,显然有
,显然有 ,进而
,进而
 。
。
从而 为扩交换超rpp半群。
为扩交换超rpp半群。
如 [1] ,称半群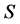 为富足半群(abundant semigroup),如果
为富足半群(abundant semigroup),如果 的每个
的每个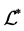 -类和每个
-类和每个 -类都含幂等元;称
-类都含幂等元;称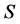 为超富足半群(superabundant semigroup),如果它的每个
为超富足半群(superabundant semigroup),如果它的每个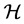 -类都含有幂等元。显然超富足半群是富足半群。关于超富足半群,读者可参见 [1] 。当
-类都含有幂等元。显然超富足半群是富足半群。关于超富足半群,读者可参见 [1] 。当 为扩交换超rpp半群时,则每个
为扩交换超rpp半群时,则每个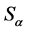 都是消去幺半群上的Rees矩阵半群,再据( [1] , Theorem4.9,Corollary5.2),
都是消去幺半群上的Rees矩阵半群,再据( [1] , Theorem4.9,Corollary5.2),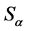 为完全
为完全 -单半群(completely
-单半群(completely 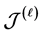 -simple semigroup),从而
-simple semigroup),从而 为完全
为完全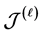 -单半群的半格。这样,下面的问题就很自然。
-单半群的半格。这样,下面的问题就很自然。
问题2.7 是否每个扩交换超rpp半群都是超富足半群?
基金项目
国家自然科学基金(11361027),江西省研究生创新基金(YC2014-S160)和江西省教育厅科研基金资助项目。
文章引用
叶火平,郭俊颖,郭小江. 超Rpp半群的核心
Cores of Super Rpp Semigroups[J]. 理论数学, 2016, 06(03): 172-176. http://dx.doi.org/10.12677/PM.2016.63026
参考文献 (References)
- 1. Fountain, J.B. (1982) Abundant Semigroups. Proceedings of London Mathematical Society, 44, 103-129.
- 2. Guo, X.J., Guo, Y.Q. and Shum, K.P. (2010) Super Rpp Semigroups. Indian Journal of Pure and Applied Mathematics, 41, 505-533. http://dx.doi.org/10.1007/s13226-010-0030-0
- 3. Guo, J.Y., Guo, X.J. and Ding, J.Y. (2015) Com-pletely -Simple Semigroups. Advances in Mathematics (China), 44, 710-718.
- 4. Guo, J.Y., Guo, X.J. and Ding, J.Y. (2015) Free Completely -Simple Semigroups. Acta Mathematica Sinica (English Series), 31, 1086-1096. http://dx.doi.org/10.1007/s10114-015-4117-8
- 5. Guo, X.J., Guo, Y.Q. and Shum, K.P. (2008) Rees Matrix Theorem for -Simple Strongly Rpp Semigroups. Asian-European Journal of Mathematics, 1, 215-223. http://dx.doi.org/10.1142/S1793557108000205
- 6. Howie, J.M. (1976) An Introduction to Semigroup Theory. Academic Press, London.
- 7. Petrich, M. and Reilly, N.R. (1999) Completely Regular Semigroups. John Wiley & Sons, Inc., New York, Chichester, Weinheim, Brisbane, Singapore, Toronto.