Pure Mathematics
Vol.07 No.04(2017), Article ID:21287,9
pages
10.12677/PM.2017.74034
A Local Existence Theorem for a Parabolic Blow-Up Inverse Problem
Yu Pan1, Xuran Meng1, Wuqing Ning*
University of Science and Technology of China, Hefei Anhui

Received: Jun. 17th, 2017; accepted: Jun. 30th, 2017; published: Jul. 7th, 2017

ABSTRACT
In this article, we study an inverse problem for a parabolic equation with blow-up initial and boundary values in the following form: . The in- verse problem is to determine the unknown function
. The in- verse problem is to determine the unknown function 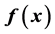 from the blow-up rates and the addi- tional observation data. In order to partly remove the blow-up data, we introduce the definition of d-line, which allows us to add the observable data and simplifies the inverse problem into a classical one. Then by establishing related functional, we prove a local existence theorem for the inverse problem in somegiven closed domain.
from the blow-up rates and the addi- tional observation data. In order to partly remove the blow-up data, we introduce the definition of d-line, which allows us to add the observable data and simplifies the inverse problem into a classical one. Then by establishing related functional, we prove a local existence theorem for the inverse problem in somegiven closed domain.
Keywords:Nonlinear Parabolic Equation, Blow-Up, Inverse Problem, Existence, d-Line

一类抛物型爆破反问题的局部存在性定理
潘宇,孟徐然,宁吴庆*
中国科学技术大学,安徽 合肥

收稿日期:2017年6月17日;录用日期:2017年6月30日;发布日期:2017年7月7日

摘 要
本文研究如下初边值条件均爆破的抛物型方程的反问题: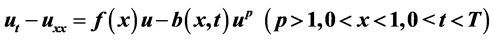 。此类反问题是由爆破速率和附加观测数据来确定未知函数
。此类反问题是由爆破速率和附加观测数据来确定未知函数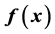 。为了部分消除爆破数据,我们引入d-线的概念以增加d-线上的观测数据,从而可将问题简化为经典的反问题。之后建立相关泛函来证明在给定的闭区域中反问题的局部存在性定理。
。为了部分消除爆破数据,我们引入d-线的概念以增加d-线上的观测数据,从而可将问题简化为经典的反问题。之后建立相关泛函来证明在给定的闭区域中反问题的局部存在性定理。
关键词 :非线性抛物方程,爆破,反问题,存在性,d-线

Copyright © 2017 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
研究非线性方程的奇异性一直在国际上深受关注,其中之一便是爆破问题, [1] [2] [3] [4] [5] 等文献对此类问题有深刻而影响广泛的研究。爆破问题的研究无论在科学理论方面还是在实际生产中都有非常重要的意义,例如文献 [6] 和 [7] 分别研究了从两类工业模型中得到的方程的爆破条件、时刻及速率。
反问题,指的是从已知结果来确定未知原因的一类问题,在物理、化学、天文、生物等自然科学中有相当重要的理论与应用价值,而在实际生活中诸如医学检查、无损探伤、资源勘探、图形恢复等方面也有广泛应用,是一个学科交叉性极强的热门研究方向。而其中的微分方程反问题,多数是指利用方程解的一些可观测资料(如初边值数据)来确定方程中的未知系数。
随着线性方程反问题探究的不断完善,人们越来越对非线性方程反问题产生浓厚的兴趣。文献 [8] 证明了非线性抛物型方程初边值问题经典解的存在唯一性,而对于相应的反问题,即利用狄利克雷与诺伊曼边界观测数据确定未知非线性项,学者们也做了大量的研究工作,主要是关于问题适定性的。关于存在性的结果可以参考 [9] ,在某些附加条件下唯一性的结果可以参考 [10] [11] [12] ,而对非线性项稳定性的结果参考 [13] 。从这些文献中可以看出,非线性方程反问题的主要特点是研究难度大—非线性方程的解会表现出非常强的复杂性,使得方程本身难以掌控。
尽管爆破方程的正问题仍是偏微分方程研究中的热点,但对于一些爆破方程的爆破速率我们无从得知,从而难入手去研究相关爆破方程的反问题。据我们所知,目前基本上没有相关反问题的研究结果被发表。对抛物型爆破正问题,1989年 [14] 首先推导出一维半线性热传导方程的有限点爆破性质, [15] 给出一类半线性抛物型方程的爆破解, [16] 提供了一维反应扩散方程的全局爆破条件, [17] 讨论了一类半线性热传导方程的爆破集合,而 [18] 则探究了初值条件和边值条件均爆破的抛物型方程的性质。以上这些文献采取的方法在理论上为本文中爆破反问题的研究奠定了坚实的基础。
为了将问题简化,我们不妨考虑空间变量 为一维的情形并研究如下抛物型逻辑斯谛方程的初边值问题:
为一维的情形并研究如下抛物型逻辑斯谛方程的初边值问题:
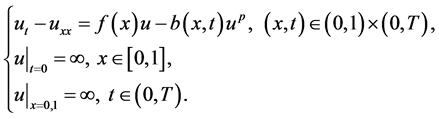 (1)
(1)
其中,常数 ,
, ,
,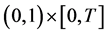 上的连续函数
上的连续函数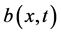 可表示某生物种群的自限性系数且满足如下条件:在
可表示某生物种群的自限性系数且满足如下条件:在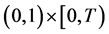 中
中 和
和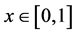 时
时 ,而这里
,而这里 上的连续函数
上的连续函数 可表示该生物种群在空间分布中的出生率。问题(1)是一个在初始时刻和边界上同时爆破的非自治系统。本文中我们主要研究如下反问题:利用问题(1)的爆破速率和附加观测数据确定未知函数
可表示该生物种群在空间分布中的出生率。问题(1)是一个在初始时刻和边界上同时爆破的非自治系统。本文中我们主要研究如下反问题:利用问题(1)的爆破速率和附加观测数据确定未知函数 。这里要说明的是我们不需要知道爆破解
。这里要说明的是我们不需要知道爆破解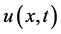 在整个存在区域的观测值。在对爆破速率作某些限定的条件下,我们对此反问题的存在性进行研究并得到如下主要结果。
在整个存在区域的观测值。在对爆破速率作某些限定的条件下,我们对此反问题的存在性进行研究并得到如下主要结果。
定理1. 设方程满足如下条件:
 (2)
(2)
其中
1) 常数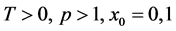 ;
;
2) ,
, ,常数
,常数 ,
, ;
;
3)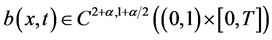 满足:
满足: 时
时 ,在
,在 中
中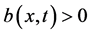 ;
;
4)存在常数 及
及 上的正值连续函数
上的正值连续函数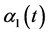 ,
,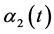 使得
使得

对所有 均成立,并且函数
均成立,并且函数 可以连续延拓到
可以连续延拓到 上;
上;
5)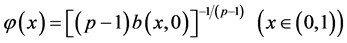 ,
,
 。
。
如果对给定的常数 和
和 成立:
成立:
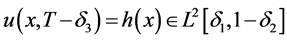 ,
,
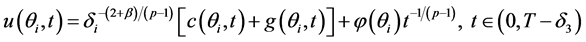 ,
,
其中 ,而
,而 满足如下四个条件:
满足如下四个条件:
(H1) 对固定的 ,有
,有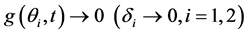 ;
;
(H2) 在 中,
中, 关于
关于 可微且与
可微且与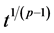 相乘得到的函数具有一定的赫尔德连续性;
相乘得到的函数具有一定的赫尔德连续性;
(H3) ;
;
(H4)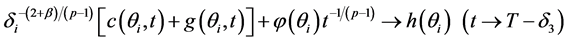 ,
,
则对给定的 ,
,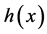 和
和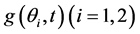 ,函数
,函数 在
在 上是存在的。
上是存在的。
注:上述定理正是此爆破反问题的局部存在性定理,这里的观察数据 和
和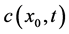 分别表示初始时刻和边界上的爆破速率,且二者均由
分别表示初始时刻和边界上的爆破速率,且二者均由 给出。另外,对函数
给出。另外,对函数 和
和 增加光滑性条件的目的是为了保证在非爆破区域中解的光滑性。
增加光滑性条件的目的是为了保证在非爆破区域中解的光滑性。
2. 前期准备
为了证明定理1,我们先做如下准备工作。
定理2.1. (勒贝格控制收敛定理)设 为一可积函数列,其极限存在:当
为一可积函数列,其极限存在:当 时,
时, ,且存在可积函数
,且存在可积函数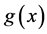 使得
使得 ,则
,则 可积,且下式成立:
可积,且下式成立:
 。
。
证明:详见文献 [19] 中P67。□
定理2.2. (关于一类非线性抛物性爆破方程的正问题解)令 为有界光滑区域,常数
为有界光滑区域,常数 。若方程满足如下4个条件:
。若方程满足如下4个条件:
1) ;
;
2) ;
;
3)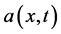 和
和 分别在
分别在 和
和 上连续,在
上连续,在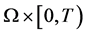 中
中 ,在
,在 中
中 ;
;
4)存在常数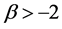 以及
以及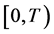 上的正值连续函数
上的正值连续函数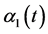 ,
, 使得
使得

对所有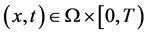 均成立,
均成立,
则
1) 对固定的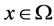 ,有
,有 ;
;
2) 若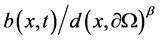 可以延拓为
可以延拓为 上的连续函数
上的连续函数 ,那么对固定的
,那么对固定的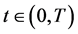 有
有
 。
。
证明:详见文献 [18] 。□
注:在定理2.2的条件下,由 [18] 知上述问题的正值解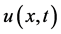 在
在 的任何紧子区域上有界,由此可推出
的任何紧子区域上有界,由此可推出 在区域内部并不爆破,而在
在区域内部并不爆破,而在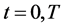 时和侧面上爆破,且
时和侧面上爆破,且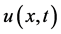 在
在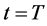 时满足同样的方程。另外,从定理2.2的结论可以看出爆破解
时满足同样的方程。另外,从定理2.2的结论可以看出爆破解 的爆破速率仅与函数
的爆破速率仅与函数 有关而与
有关而与 无关。因此,为了研究爆破反问题必须要增加其它观测数据。
无关。因此,为了研究爆破反问题必须要增加其它观测数据。
若在定理2.2中取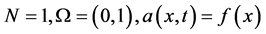 ,则如下推论成立。
,则如下推论成立。
推论2.1. (特定方程正问题的解)若方程满足如下4个条件:
1)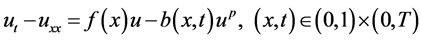 ;
;
2) ;
;
3) 和
和 分别在
分别在 和
和 上连续,在
上连续,在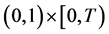 中
中 ,在
,在 中
中 ;
;
4) 存在常数 以及
以及 上的正值连续函数
上的正值连续函数 ,
, 使得
使得
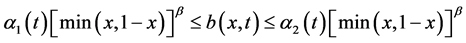
对所有 均成立,
均成立,
则
1) 对固定的 ,有
,有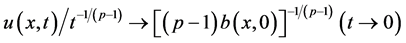 ;
;
2) 若 可以延拓为
可以延拓为 上的连续函数
上的连续函数 ,那么对固定的
,那么对固定的 有
有
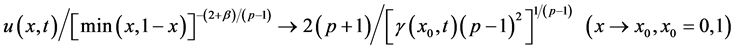 。
。
3. 定理1的证明
对于定理1,我们将分成4个步骤来进行证明。
3.1. 方程初边值条件的合理性检验
对于问题(2)中的初边值条件,由定理1中所给的条件易知推论2.1的条件1)~4)是满足的,因此,由推论2.1的结论可知问题(2)的爆破速率 和
和 存在且在任一闭子区间上有界,即合理性满足。
存在且在任一闭子区间上有界,即合理性满足。
3.2. 方程初值条件的非爆破化处理
令 ,则可以得到
,则可以得到 ,在
,在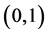 的任一闭子区间上有界。将
的任一闭子区间上有界。将 代入(2)可得
代入(2)可得
 (3)
(3)
如图1,图2所示,在进行非爆破化处理之后, 中的初值条件不再爆破。
中的初值条件不再爆破。
图1. 
图2. 
3.3. d-线模型及增加必要观测数据
对给定的常数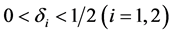 及
及 ,如图3所示,设
,如图3所示,设 围成的矩形部分为d-域,其竖直边界线为两条d-线。要研究该方程的反问题,因边界的爆破,无法从边界直接入手,但我们可以考虑距离边界很近的两条d-线,解在d-线上不爆破,可以对其做出一些观测,即把问题(3)中的条件(*)换成如下条件:在d-线上,
围成的矩形部分为d-域,其竖直边界线为两条d-线。要研究该方程的反问题,因边界的爆破,无法从边界直接入手,但我们可以考虑距离边界很近的两条d-线,解在d-线上不爆破,可以对其做出一些观测,即把问题(3)中的条件(*)换成如下条件:在d-线上,
 ,
,
 。
。
其中函数 在
在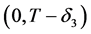 上连续,可以看成是边界爆破速率
上连续,可以看成是边界爆破速率 的近似观测值:
的近似观测值:
 。
。
这里 是已知的观测数据,且满足如下条件:
是已知的观测数据,且满足如下条件:
(H1) 对固定的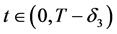 ,有
,有 ;
;
(H2) 在 中,
中,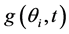 关于
关于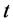 可微且与
可微且与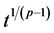 相乘得到的函数具有一定的赫尔德连续性;
相乘得到的函数具有一定的赫尔德连续性;
(H3) ;
;
(H4)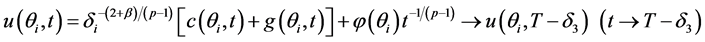 ,
,
由定理1的条件知在上面的条件(H3)中函数 在
在 上是有界的,而(H4)的合理性可由定理2.2的注记得到。另外,利用
上是有界的,而(H4)的合理性可由定理2.2的注记得到。另外,利用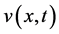 的定义,问题(3)的初值条件以及
的定义,问题(3)的初值条件以及 所满足的条件可以得知:当
所满足的条件可以得知:当 时,
时, 以及
以及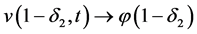 。这样在d-域内问题(3)的相容性是满足的。由此可知,在d-域上
。这样在d-域内问题(3)的相容性是满足的。由此可知,在d-域上 的初边值均不是爆破的,从而可将原爆破反问题转化为经典的反问题来解决。
的初边值均不是爆破的,从而可将原爆破反问题转化为经典的反问题来解决。
综上所述,我们得到如下关于 的初边值问题:
的初边值问题:
 (4)
(4)

Figure 3. d-domain
图3. d-域
由定理2.2,文献 [8] ,定理1条件以及 的条件,可以得到如下结论:
的条件,可以得到如下结论:
在d-域上, (5)
(5)
从而对于非线性抛物方程的经典定解问题(4),方程右端的 在d-域上是赫尔德连续的。
在d-域上是赫尔德连续的。
基于上述观察与分析,当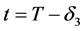 时,我们增加如下观测数据(超定数据):
时,我们增加如下观测数据(超定数据):

本文的主要目的是要证明在给定 ,
, 和
和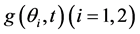 的情况下未知函数
的情况下未知函数 的存在性。
的存在性。
3.4. 反问题存在性的证明
关于定理1的证明方法,我们主要参考2009年文献 [20] 中的最优控制法,主要思路是将此爆破反问题解的存在性转化为某个最优控制问题极小元的存在性。为此,下面我们首先令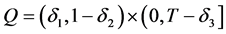 ,那么我们可以证明如下结果:
,那么我们可以证明如下结果:
定理3.1. 存在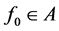 使得
使得 , 其中泛函
, 其中泛函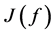 定义如下:
定义如下:
 ,
,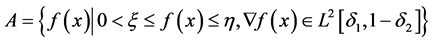 。
。
这里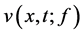 是问题(4)关于任意给定的
是问题(4)关于任意给定的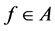 的解,
的解,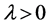 为正则化参数,
为正则化参数, 为给定常数。
为给定常数。
证明:显然,泛函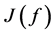 非负且存在下确界
非负且存在下确界 。考虑极小化序列
。考虑极小化序列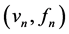 ,满足如下关系式:
,满足如下关系式:
 。
。
注意到 ,以下
,以下 表示不依赖于
表示不依赖于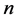 的常数(可以不同)。由
的常数(可以不同)。由 的定义易得
的定义易得
 。
。
从而由索伯列夫嵌入定理知
 。
。
因此,由上式及(5)知
 ,
,
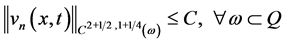 。
。
由巴拿赫空间理论,我们可以选取一子列,仍记为 ,满足:对给定的常数
,满足:对给定的常数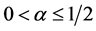 ,当
,当 时,
时,
 ,在
,在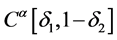 上一致收敛,
上一致收敛,
 ,在
,在 上一致收敛。
上一致收敛。
利用上述函数列一致收敛性易知极限函数对 满足问题(4)。
满足问题(4)。
由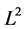 范数的下半连续性及勒贝格控制收敛定理得:
范数的下半连续性及勒贝格控制收敛定理得:
 。
。
既然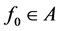 ,即得
,即得 。定理3.1证毕。□
。定理3.1证毕。□
当给定的函数 ,
,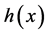 和
和 满足定理1的条件时,由定理3.1知存在
满足定理1的条件时,由定理3.1知存在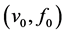 满足问题(4)且
满足问题(4)且 ,此时若令
,此时若令 ,则在d-域上
,则在d-域上 满足问题(2),由此证明了
满足问题(2),由此证明了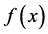 在
在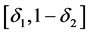 上的存在性。定理1证毕。□
上的存在性。定理1证毕。□
注:关于抛物型方程的反系数问题,我们还可以参考文献 [21] 。另外,我们猜测当 且爆破速率满足(4)中的条件时,此爆破反问题的解
且爆破速率满足(4)中的条件时,此爆破反问题的解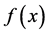 在d-域中是局部稳定的,相关的研究工作仍在进行中。
在d-域中是局部稳定的,相关的研究工作仍在进行中。
4. 结论
4.1. 阐述d-线意义
在一般的爆破问题中,由于边界的爆破性,无法直接得到数据。为研究爆破反问题,我们引入了d-线,其意义在于将爆破反问题转化为经典的非爆破反问题。通过d-线法可将未知系数的存在性确定在d-域之中,因此,对爆破方程反问题而言d-线的引入在很大程度上是为了精确系数存在的范围。在真实的工业生产中,例如仪器的边界不可测,可通过d-线法,将仪器的故障排除在d-域之外—可令 值不断减小来精确故障的所在范围。
值不断减小来精确故障的所在范围。
4.2. 结论与开放性问题
本文利用d-线法将一类爆破反问题转化为经典的非爆破反问题,并证明了在特定条件下爆破反问题的存在性。同时,本文证明的思路对讨论d-域内反问题的唯一性与稳定性具有很重要的参考价值。最后,因缺乏适当的观测数据,函数 在
在 上仍是未知的,所以,当
上仍是未知的,所以,当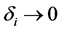 时如何处理相应的爆破反问题仍是一个具有挑战性的课题。
时如何处理相应的爆破反问题仍是一个具有挑战性的课题。
基金项目
本文由中国科学技术大学校级预研项目16年(编号:YZ3471500010)部分资助。
文章引用
潘宇,孟徐然,宁吴庆. 一类抛物型爆破反问题的局部存在性定理
A Local Existence Theorem for a Parabolic Blow-Up Inverse Problem[J]. 理论数学, 2017, 07(04): 262-270. http://dx.doi.org/10.12677/PM.2017.74034
参考文献 (References)
- 1. Escobedo, M. and Velázquez, J.J.L. (2015) Finite Time Blow-Up and Condensation for the Bosonic Nordheim Equation. Inventiones Mathematicae, 200, 761-847. https://doi.org/10.1007/s00222-014-0539-7
- 2. Giga, Y. and Kohn, R.V. (1985) Asymptotic Self-Similar Blow-Up of Semilinear Heat Equations, Communications on Pure and Applied Mathematics, 38, 297-319. https://doi.org/10.1002/cpa.3160380304
- 3. Martel, Y. and Merle, F. (2002) Stability of Blow-Up Profile and Lower Bounds for Blow-Up Rate for the Critical Generalized KdV Equation. Annals of Mathematics, 155, 235-280. https://doi.org/10.2307/3062156
- 4. Merle, F. and Raphael, P. (2005) The Blow-Up Dynamic and Upper Bound on the Blow-Up Rate for Critical Nonlinear Schrödinger Equation. Annals of Mathematics, 161, 157-222. https://doi.org/10.4007/annals.2005.161.157
- 5. Xin, Z. (1998) Blowup of Smooth Solutions to the Compressible Navi-er-Stokes Equation with Compact Density. Communications on Pure and Applied Mathematics, 51, 229-240. 3.0.CO;2-C>https://doi.org/10.1002/(SICI)1097-0312(199803)51:3<229::AID-CPA1>3.0.CO;2-C
- 6. 江成顺, 汪先超. 伪抛物型方程非局部问题解的爆破性[J]. 理论数学, 2011, 1(2): 80-84.
- 7. 靳妞, 张宏伟, 呼青英. 动力边界条件的阻尼波动方程解的爆破性和渐近性[J]. 理论数学, 2012, 2(3): 144-151.
- 8. Ladyzenskaja, O.A., Solonnikov, V.A. and Uralceva, N.N. (1968) Linear and Quasi-linear Equations of Parabolic Type. American Mathematical Society, Providence.
- 9. Pilant, M.S. and Rundell, W. (1986) An Inverse Problem for a Nonlinear Parabolic Equation. Communications in Partial Differential Equations, 11, 445-457. https://doi.org/10.1080/03605308608820430
- 10. Cannon, J.R. and DuChateau, P. (1998) Structural Identification of an Unknown Source Term in a Heat Equation. Inverse Problems, 14, 535-551. https://doi.org/10.1088/0266-5611/14/3/010
- 11. DuChateau, P. and Rundell, W. (1985) Unicity in an Inverse Problem for an Un-Known Reaction Term in a Reaction-Diffusion Equation. Journal of Differential Equations, 59, 155-164.
- 12. Klibanov, M.V. (2004) Global Uniqueness of a Multidimensional Inverse Problem for a Nonlinear Parabolic Equation by a Carleman Estimate. Inverse Problems, 20, 1003-1032. https://doi.org/10.1088/0266-5611/20/4/002
- 13. Choulli, M., Ouhabaz, E.M. and Yamamoto, M. (2006) Stable Determination of a Semilinear Term in a Parabolic Equation. Communications on Pure and Applied Analysis, 5, 447-462. https://doi.org/10.3934/cpaa.2006.5.447
- 14. Chen, X. and Matano, H. (1989) Convergence, Asymptotic, and Finite-Point Blow-Up in One-Dimensional Semilinear Heat Equations. Journal of Differential Equations, 78, 160-190.
- 15. Du, Y. and Huang, Q. (1999) Blow-Up Solutions for a Class of Semilinear Elliptic and Parabolic Equations. SIAM Journal on Mathematical Analysis, 31, 1-18. https://doi.org/10.1137/S0036141099352844
- 16. Fiedler, B. and Matano, H. (2007) Global Dynamics of Blow-Up Profiles in One-Dimensional Reaction Diffusion Equations. Journal of Dynamics and Differential Equations, 19, 867-893. https://doi.org/10.1007/s10884-007-9083-0
- 17. Fujishima, Y. and Ishige, K. (2010) Blow-Up Set for a Semilinear Heat Equation with Small Diffusion. Journal of Differential Equations, 249, 1056-1077.
- 18. Du, Y., Peng, R. and Polacik, P. (2012) The Parabolic Logistic Equation with Blow-Up Initial and Boundary Values. Journal d’Analyse Mathématique, 118, 297-316. https://doi.org/10.1007/s11854-012-0036-0
- 19. Stein, E.M. and Shakarchi, R. (2005) Real Analysis: Measure Theory, Integration and Hilbert Spaces. Princeton University Press, Princeton.
- 20. Deng, Z., Yang, L., Yu, J. and Luo, G. (2009) An Inverse Problem of Identifying the Coefficient in a Nonlinear Parabolic Equation. Nonlinear Analysis, 71, 6212-6221.
- 21. 肖翠娥, 许友军. 抛物型方程的反系数问题研究[J]. 理论数学, 2011, 1(2): 144-148.
NOTES
*通讯作者。