Pure Mathematics
Vol.
10
No.
03
(
2020
), Article ID:
34554
,
8
pages
10.12677/PM.2020.103027
Tetrapartite Entanglement of an Open Quantum System in Accelerated Frames
Meng Shi*, Haimei Zhong
Mathematics Institute, South China University of Technology, Guangzhou Guangdong
Received: Feb. 22nd, 2020; accepted: Mar. 10th, 2020; published: Mar. 17th, 2020

ABSTRACT
In this paper, we mainly study the entanglement of tetrapartite GHZ quantum states in an open environment in a noninertial system, and explore the entanglement changes when the three observers accelerate, and when the system A and system AB contact with the environment. Then we explore the entanglement changes of four observers when they all accelerate, only when the system A contacts the environment.
Keywords:Entanglement, GHZ-State, Phase Damping

在非惯性系下开放环境中的四体纠缠
史萌*,钟海梅
华南理工大学数学学院,广东 广州
收稿日期:2020年2月22日;录用日期:2020年3月10日;发布日期:2020年3月17日

摘 要
本文主要研究了四体GHZ量子态在开放环境中非惯性系下的纠缠变化,探究了当三个观察者加速时,系统A和系统AB与环境接触时,纠缠的变化情况。接着探究了当四个观察者加速时,只有系统A与环境接触时,它们的纠缠变化情况。
关键词 :纠缠,GHZ态,相位阻尼

Copyright © 2020 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
在量子计算和量子信息中,纠缠是一个很重要的概念 [1] [2] [3]。近些年来随着对量子信息科学和相对论的进一步研究,人们开始研究在非惯性系下的多体态的物理特征。量子系统的纠缠不可避免的受到外界环境的影响,所以人们研究了二体或者三体量子态在环境下的纠缠变化 [4],也得到了一些纠缠的变化特征。
本文主要研究了四体GHZ量子态在开放环境中非惯性系下的纠缠变化,探究了当三个观察者加速时,系统A和系统AB与环境接触时,纠缠的变化情况。接着探究了当四个观察者加速时,只有系统A与环境接触时,它们的纠缠变化情况。最后比较了当只有系统A与环境接触时,当有三个观察者和四个观察者时,它们的纠缠变化情况。
2. 基本概念与知识
在非惯性系下,Rindler坐标适合描述一类具有均匀加速的观察者,而另一个保持惯性系的观察者可以用Minkowski坐标描述。我们利用单模近似模型,将Minkowski空间的真空态 和单粒子态 转化为Rindler空间的粒子态的张量积的形式,通过变换运算符,可以得到下列运算关系 [5]:
(1)
(2)
其中 ,式子中的 分别代表加速观察者的加速度和加速参数,w代表对应的频率。另一方面加速观察者是在Rindler区域一,与Rindler区域二是不相联系的,对不相关的区域二求迹,可以得到所需要的四体态。
接下来介绍计算纠缠的测量方法。对于一个多体系统 ,我们常用的测量是负度 [6],它的定义如下:
(3)
(4)
另一方面,对于一个矩阵M, 是它的所有负的特征值,有下面的公式:
所以等式(3)和(4)可以改写如下形式:
剩余纠缠定义如下 [5]:
一般 ,于是 -纠缠定义为:
用类似于上述定义纠缠度的方法,我们可以把定义扩展到四个量子位,定义如下 [7]:
因此我们可以定义总的纠缠:
由于开放的量子系统总是处在复杂的环境中,本文所涉及的环境是:相位阻尼环境,在这里的子系统分别只与自己的环境相互作用,与其他子系统不相互交流。相位阻尼环境有如下形式:
其中i是从1到N的整数,也表示第i个系统的相位阻尼算符, 是一个与时间有关的参数。另外系统与环境之间的相互作用可以写成下列关系式:
(5)
其中 是量子系统没有与环境接触就出之前所处的状态, 是与环境作用后的系统的状态。
3. 四体GHZ态与相位阻尼环境作用只有三个观察者加速
我们将考虑由Alice,Bob,Charlie 和Daniel四个观察者共享的四体GHZ态,定义如下:
其中GHZ态的下标 分别代表四个观察者。当只有Bob,Charlie和Daniel这三个观察者都以相同的加速参数r加速时,我们运用式子(1)和(2),并通过对区域二分别求偏迹,可以得到下面量子态:
接下来量子态 中只有A系统与相位阻尼环境相接触,运用式子(5),可以得到与环境作用后的态,再通过分别对四个子系统求部分转置,可以得到下列矩阵:
经过一些计算,我们可以得到:
从下面的图1中我们可以看出,只有系统A与环境接触,对于加速参数r分别取三个特殊值,随着退化参数p增大, 都是减少的,最后都是减少到0,没有纠缠。对于相同的退化参数p,加速参数r越大,相应的纠缠度就越小。 的变化趋势如图2所示,它随着加速参数r和退化参数p也是逐步减少。类似上面的的算法,我们假设系统A和BI都与相同的相位阻尼环境相接触,通过计算得到:
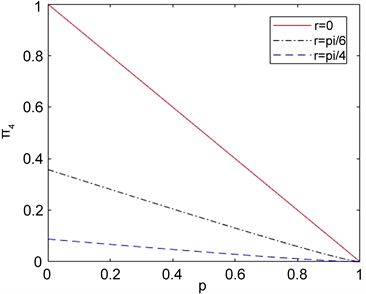
Figure 1. Curve: 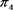 as a function of the acceleration p for the phase damping environment
as a function of the acceleration p for the phase damping environment
图1. 对于相位阻尼环境,纠缠随退化参数变化的情况
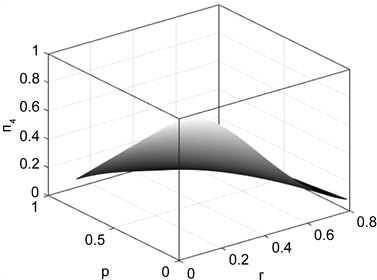
Figure 2. Curve: as a function of the acceleration p for the phase damping environment
图2. 对于相位阻尼环境,纠缠随退化参数变化的情况
由于其他的纠缠公式比较复杂,所以没有写出来, 如图3所示,它也是随着退化参数减少到0,从图中可以看出加速参数最大的, 最先减少到0。
接下来当 ,两种情况的 的变化情况如图4所示,黑色曲线表示只有系统A与环境接触的情况,蓝色曲线表示系统AB与相同环境接触时的情况,从图中可以看出当 ,两种情况刚开始纠缠度是一样的,随着p的增大,与环境接触的系统越多,也就是当系统AB都与环境接触,纠缠程度下降的越快,当p接近0.85时, 减少到0。
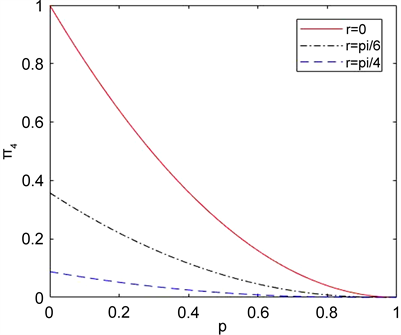
Figure 3. Curve:  as a function of the acceleration p for the phase damping environment
as a function of the acceleration p for the phase damping environment
图3. 对于相位阻尼环境,纠缠随退化参数变化的情况
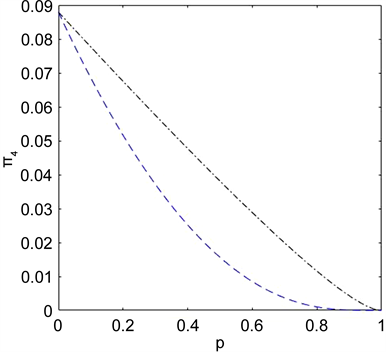
Figure 4. Curve: as a function of the acceleration p for the phase damping environment
图4. 对于相位阻尼环境,纠缠随退化参数变化的情况
4. 四体GHZ态与相位阻尼环境作用四个观察者都加速
当四个观察者Alice,Bob,Charlie和Daniel都加速时,加速参数分别是 ,GHZ态变成下列形式:
为了方便计算,我们让 ,仅仅只让系统A与相位阻尼环境作用,其他的系统不与环境接触,通过运用等式(5),再对区域二求偏迹后,得到下列式子:
再通过分别对系统 求偏转置,得到它们的矩阵,再通过一些计算可以得到:
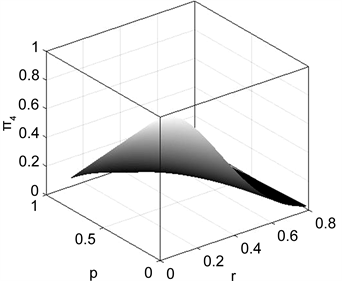
Figure 5. Curve: as a function of the acceleration p,r for the phase damping environment
图5. 对于相位阻尼环境,纠缠随退化参数变化的情况
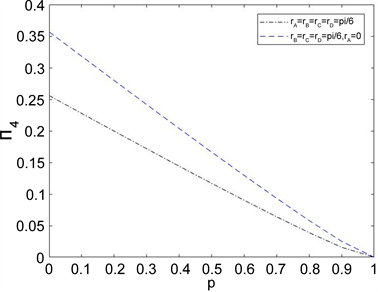
Figure 6. Curve: asa function of the acceleration p for the phase damping environment
图6. 对于相位阻尼环境,纠缠随退化参数变化的情况
这四个纠缠度量的数都是相等的,所以通过计算发现二体纠缠都为0,也即:
图形如图5所示,纠缠度随着参数 逐渐减少到0,纠缠完全被破坏。
对于GHZ态,接下来我们讨论当仅仅只有系统A与环境接触时,有三个观察者加速时和全部都加速时,它们的加速参数都是 ,纠缠度情况变化如图6所示。从图中可以看到当 ,只有三个观察者加速时,初始总纠缠度大于0.35,而当全部观察者都加速时,初始总纠缠数接近0.25。随着加速参数的逐渐增大, 几乎同时逐渐减少到0。我们可以看出环境对纠缠度的影响是大于加速度的。
文章引用
史 萌,钟海梅. 在非惯性系下开放环境中的四体纠缠
Tetrapartite Entanglement of an Open Quantum System in Accelerated Frames[J]. 理论数学, 2020, 10(03): 201-208. https://doi.org/10.12677/PM.2020.103027
参考文献
- 1. Bouwmeester, D., Ekert, A.K. and Zeilinger, A. (2013) The Physics of Quantum Information: Quantum Cryptography, Quantum Teleportation, Quantum Computation. Studies in History and Philosophy of Modern Physics, 34, 331-334. https://doi.org/10.1016/S1355-2198(03)00012-1
- 2. Peres, A. and Terno, D.R. (2004) Quantum Information and Relativity Theory. Review of Modern Physics, 76, 93-123. https://doi.org/10.1103/RevModPhys.76.93
- 3. Takagi, S. (1986) Vacuum Noise and Stress Induced by Uniform Acceleration: Hawking-Unruh Effect in Rindler Manifold of Arbitrary Dimension. Progress of Theoretical Physics Supplement, 88, 1-142. https://doi.org/10.1143/PTPS.88.1
- 4. Zhang, W. and Jing, J. (2011) Multipartite Entanglement for Open System in Noninertial Frames. arXiv:quant-ph/1103.4903 https://doi.org/10.1103/PhysRevA.83.022314
- 5. Wang, J. and Jing, J. (2011) Multipartite Entanglement of Fermionic Systems in Noninertial Frames. Physical Review A, 83, 334-344. https://doi.org/10.1103/PhysRevA.83.022314
- 6. Vidal, G. and Werner, R.F. (2002) A Computable Measure of Entanglement. Physical Review A, 65, Article ID: 032314. https://doi.org/10.1103/PhysRevA.65.032314
- 7. Li, Y., Liu, C., Wang, Q., Zhang, H. and Hu, L. (2016) Tetrapartite Entanglement of Fermionic Systems in Noninertial Frames. Optik-International Journal for Light and Electron Optics, 127, 9788-9797. https://doi.org/10.1016/j.ijleo.2016.07.069
NOTES
*第一作者。