Pure Mathematics
Vol.
11
No.
01
(
2021
), Article ID:
39822
,
6
pages
10.12677/PM.2021.111008
S-Poset内射包的一个注记
李玉林
长安大学理学院,陕西 西安

收稿日期:2020年12月12日;录用日期:2021年1月11日;发布日期:2021年1月18日

摘要
设S是一个序半群,本文采用序代数理论和quantale理论中的研究方法,在以S-poset为对象以S-次可乘映射为态射的范畴中,对于一类特殊的态射 ,构造了S-poset的内射包。本文的结果不仅推广了基于S是序幺半群时的相应结果,而且也得到了剩余S-poset的内射包。
关键词
序半群,S-Poset,内射包

A Note on Injective Hulls of S-Poset
Yulin Li
School of Science, Chang’an University, Xi’an Shaanxi

Received: Dec. 12th, 2020; accepted: Jan. 11th, 2021; published: Jan. 18th, 2021

ABSTRACT
Let S be a posemigroup. Inspired by the study method of order algebra theory and quantale theory, we construct an -injective hull for an arbitrary S-poset in the category of S-poset with S-submultiplicative morphisms with respect to a specific class of morphisms . The results of the present paper not only generalize the corresponding results based on S be a pomonoid but also lead to injective hull for residuated S-poset.
Keywords:Posemigroup, S-Poset, Injective Hull

Copyright © 2021 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
受群作用和环的模理论研究的启发,在众多的学科中都产生了半群作用相关结构。因此在不同的领域半群作用有着不同的名称,比如:S-自动机,S-操作数,S-多边形,S-集,S-代数等 [1] [2] [3] [4]。作为半群作用与偏序集理论的结合,S-poset理论近年来得到了发展 [5] - [10]。粗略地说,S-poset是一个带有序半群S-作用并且满足一定的相容条件的偏序集。
内射性是重要的范畴性质,在以S-poset为对象的范畴中,内射性也得到了众多的关注与研究 [1] [5] [6] [7] [11]。目前对于该范畴的研究,S通常被假定为一个序幺半群,带有的态射不同,该范畴的性质相应的也不同。为了得到以S-poset为对象的范畴中的内射对象的完整刻画,在文献 [11] 中,研究了以S-poset为对象以S-次可乘映射为态射构成的范畴中的内射对象,并进一步得到了S-poset相对于一类 态射的内射包。但,文献 [11] 中的主要结果是基于S为序幺半群得到的,因此,一个自然的问题是,这些结果能否推广到S是一般的序半群上,这是本文的主要动机。在以S-poset为对象以S-次可乘映射为态射构成的范畴中,对于一类特殊的态射 ,本文构造了任意S-poset的内射包。
2. 预备知识
设P是一个偏序集 [12], ,定义 。如果 ,则称A为下集。 。本文用到的其它有关偏序集的概念和结论请参考文献 [12]。
定义2.1 [13] 设 是半群, 是偏序集。如果 关于半群的乘法 是相容的,即 ,有 ,则称 为序半群。进一步,如果 是一个幺半群,则称 是序幺半群。
如果没有特别说明,本文中的 均为序半群, 表示一个序幺半群带有幺元1。
定义2.2 [5] 设 是一个偏序集, 是一个映射( , 记为 )。如果对任意的 ,满足以下条件:
(1) ;
(2) ,
则称 为S-poset,为方便简记为 或A。如果 是一个序幺半群,S1-poset A还需满足: 。
定义2.3 [11] 设 是S-poset, 是完备格,且 ,都有 ,则称 是一个S-quantale。 有伴右随,记为 。
设 和 是S-poset,称映射 是S-可乘的(相应的,S-次可乘的),如果 , (相应的, )。
设 和 是S-poset,称映射 是S-poset同态(相应的S-poset次同态),如果 是保序映射且f是S-可乘的(相应的,S-次可乘的)。
以S-poset为对象以S-poset同态为态射的范畴记为 。
以S-poset为对象以S-poset次同态为态射的范畴记为 。
定义2.4 [14] 设 是一个范畴,M是 中的一个态射类,
1) 称 中的对象C为M-内射的,如果对M中的任意态射 以及 中的态射 ,都存在唯一的态射 使得 。
2) 称M中的态射 为M-本质的,如果对 中任意态射 , 有 。
3) 对于 中的对象A的和对象B,称对象B是对象A的M-内射包,如果对象B是M-内射的,且存在一个M-本质态射 。
有关范畴的相关知识,本文未作解释的请参考文献 [14]。
3. 主要结果
注意本文中的S是一个序半群而不是序幺半群。但是根据文献 [11],我们可以得到一系列相似的结论。为简明起见,我们省掉类似的证明。
设 表示是序嵌入的S-poset同态构成的类。设 表示范畴 中满足条件: , 的态射构成的类。显然, 。
通过类似于文献 [11] 中命题4和命题5的证明,可以得到以下结论:
命题3.1 (1)设 是一个S-quantale,则 在范畴 中是 -内射的。
(2) 在范畴 中,每个S-quantale的收缩是S-quantale。
对任意一个偏序集P, 表示P的所有下集组成的集合。设 是一个S-poset。对任意的 ,定义
.
.
可以证明 也是一个S-quantale。因此,由命题3.1我们可以知道 在范畴 中是 -内射的。而且,类似于文 [11] 中定理7的证明,可知 在范畴 中是 -内射的当且仅当 是一个S-quantale。
回忆一下偏序集P上的映射 被称为P上的闭包算子,如果j是保序的,增值的,幂等的。令 ,即 。如果j是P上的闭包算子,则 ,。有关闭包算子的更多性质,请参考文献 [12]。
设 是S-poset,如果j是 上的闭包算子,且j是S-次可乘的,则j被称为 上的核映射。容易得到如下的结论:
1) 设j是S-poset 上的核映射,则 ,。
2) 设j是S-quantale 上的核映射,则 是S-quantale,其中, ,。
设 是S-poset,对任意的 ,定义
;
;
.
引理3.2设 是S-poset,则 是S-quantale 上的核映射,且 ,。
证明:容易验证 和 是 上的闭包算子。所以 是 上的闭包算子。设 ,为证明 ,只需证明 。
(1) 设 ,则 。因为 ,所以 ,从而 ,因此 。
(2) 设 ,则 。所以 。从而 。
由(1) (2)可知 。
(3) 设 ,则 。设 ,则 ,即 ,所以 ,从而 。因此 。
由引理3.2,可以得到如下的命题:
命题3.3设 是S-poset,则 是一个S-quantale。因此 在范畴 中是 内射的。
设 是S-poset,定义一个映射 为:
.
定理3.4设 是S-poset,则 是 在范畴 中的 -内射包。
证明:只需证明 是 -本质的。
(1) 设 ,则 。所以 是S-次可乘的。又因为 是序嵌入,从而, ,因此 。
(2) 设 是S-poset次同态,且 。要证明 ,只需证明 ,。
设 ,,则 ,。
(i) 设 ,则 。对任意的 ,有
因为
,从而
。由d的任意性可知
,所以
。对任意的
,有
,从而
,所以 。由于x的任意性,因此,
。由于x的任意性,因此,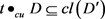 。
。
(ii) 设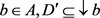 ,对任意的
,对任意的 ,有
,有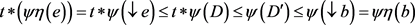 。由假设
。由假设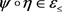 ,可得
,可得 。因此
。因此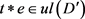 。
。
由于e的任意性,从而 ,所以
,所以 。因此
。因此 。
。
由(i)~(ii)可得 。
。
引理3.5在S1-poset 中,
中, 。
。
证明:设 ,设
,设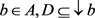 ,则
,则 。从而
。从而 ,所以
,所以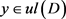 。所以
。所以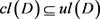 。因此
。因此 。
。
通过定理3.4,引理3.5,可以重新得到文献 [11] 的主要结论。
命题3.6设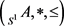 是S1-poset,则
是S1-poset,则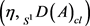 是
是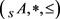 在范畴
在范畴 中的
中的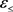 内射包。
内射包。
定义3.7设 是S-poset,如果对任意的
是S-poset,如果对任意的 ,
,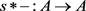 有右伴随,即有一个映射
有右伴随,即有一个映射 ,使得对任意的
,使得对任意的 ,
, ,则称S-poset
,则称S-poset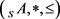 为剩余S-poset。
为剩余S-poset。
引理3.8在剩余S-poset 中,
中, 。
。
证明:设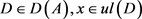 。设
。设 。则
。则 。
。 ,
, ,即
,即 ,从而,
,从而,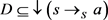 。由假设
。由假设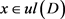 ,可得
,可得 ,即
,即 ,从而
,从而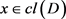 ,所以
,所以 ,因此
,因此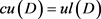 。
。
由定理3.4和引理3.8,我们可以得到如下的结论。
命题3.9设 是一个剩余S-poset,则
是一个剩余S-poset,则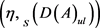 是
是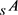 在范畴
在范畴 中的
中的 -内射包。
-内射包。
推论3.10在剩余S1-poset 中,
中, 。
。
4. 结论
本文运用序代数理论的相关知识,构造出了S-poset的内射包。并推广到S是序幺半群时的相应结果,最后得到剩余S-poset的内射包。
文章引用
李玉林. S-Poset内射包的一个注记
A Note on Injective Hulls of S-Poset[J]. 理论数学, 2021, 11(01): 47-52. https://doi.org/10.12677/PM.2021.111008
参考文献
- 1. Skornyakov, L.A. (1986) Injectivity of All Ordered Left Polygons over a Monoid. Vestnik Moskovskogo Universiteta, Seriya I, 3, 17-19.
- 2. Kilp, M., Knauer, U. and Mikhalev, A.V. (2000) Monoids, Acts and Categories (With Appli-cations to Wreath Products and Graphs). Walter de Gruyter, Berlin, New York. https://doi.org/10.1515/9783110812909
- 3. 王蕊, 赵彬. Quantale代数及其代数理想[J]. 模糊系统与数学, 2010, 24(2): 44-49.
- 4. 李伟. S-代数的表示范畴[J]. 西南大学学报(自然科学版), 2010, 32(4): 101-104.
- 5. Fakhruddin, S.M. (1998) On the Category of S-Posets. Acta Mathematica Scientia, 52, 85-92.
- 6. Zhang, X. and Laan, V. (2007) On Homological Classification of Pomonoids by Regular Weak Injectivity Properties of S-Posets. Central European Journal of Mathematics, 5, 181-200. https://doi.org/10.2478/s11533-006-0036-3
- 7. Ebrahimi, M.M., Mahmoudi, M. and Rasouli, H. (2010) Banaschewski’s Theorem for S-Posets: Regular Injectivity and Completeness. Semigroup Forum, 80, 313-324. https://doi.org/10.1007/s00233-010-9207-4
- 8. 张霞, 徐彦涛. 偏序群S上S-偏序系的内射包[J]. 华南师范大学学报(自然科学版), 2014, 46(4): 12-15.
- 9. 武全, 赵彬. 模糊S-偏序集的内射壳[J]. 吉林大学学报(理学版), 2017, 55(2): 216-224.
- 10. 毛徐新, 徐罗山. S-超连续偏序集的性质及等价刻画[J]. 计算机工程与应用, 2015, 51(1): 9-12.
- 11. Zhang, X. and Laan, V. (2015) On Injective Hulls of S-Posets. Semigroup Forum, 91, 62-70. https://doi.org/10.1007/s00233-014-9646-4
- 12. Davey, B.A. and Priestley, H.A. (2002) Introduction to Lattices and Order. Cambridge University Press, Cambridge. https://doi.org/10.1017/CBO9780511809088
- 13. 谢祥云. 序半群引论[M]. 北京: 科学出版社, 2001.
- 14. Adámek, J., Herrlich, H. and Strecker, G.E. (1990) Abstract and Concrete Categories: The Joy of Cats. Wiley, New York.