Modern Physics
Vol.07 No.04(2017), Article ID:21440,7
pages
10.12677/MP.2017.74016
Geometric Phase in an Imaginary Photon Process
Yuanxin Qiao, Zhaoxian Yu
Faculty of Science, Beijing Information Science and Technology University, Beijing

Received: Jul. 3rd, 2017; accepted: Jul. 17th, 2017; published: Jul. 21st, 2017

ABSTRACT
By using the Lewis-Riesenfeld invariant theory, we have studied the geometric phase in a generalized time-dependent Jaynes-Cummings model with imaginary photon process for two-level atoms interacting with light field. It is found that the geometric phase in a cycle case has nothing to do with the frequency of the photon field, the coupling coefficient between photons and atoms, and the atom transition frequency.
Keywords:Geometric Phase, Generalized Jaynes-Cummings Model
虚光子过程中的几何相位
乔元新,于肇贤
北京信息科技大学理学院,北京
收稿日期:2017年7月3日;录用日期:2017年7月17日;发布日期:2017年7月21日

摘 要
利用Lewis-Riesenfeld不变量理论,研究了推广的含时二能级虚光子过程的 Jaynes-Cummings模型。发现周期情况下的几何相位与光子场的频率、光子和原子之间的耦合系数以及原子跃迁频率无关。
关键词 :几何相位,推广的Jaynes-Cummings模型

Copyright © 2017 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
众所周知,几何相位的概念首先由Pancharatnam [1] 在研究经典光在不同极化状态下的干涉时引入。Berry [2] 在循环绝热演化的情况下发现了Pancharatnam相的量子对应。Aharonov和Anandan [3] 对其进行了扩展并发展了非绝对热循环演化。Samuel等人 [4] 通过将纯态几何相位扩展到非循环演化和顺序投影测量来推广。Mukunda和Simon [5] 通过将在状态空间中穿过的路径作为几何相位的主要概念给出了运动学方法。在放松绝热,单一性,和进化的周期性的情况下,已经进行了进一步的推广与改进 [6] 。目前,对在混合状态下的几何相位 [7] [8] [9] 也进行了研究。
众所周知,Lewis和Riesenfeld提出的量子不变理论 [10] 是一个有用的工具,可以用来处理与时间相关的哈密顿算子的系统。通过介绍基本不变量的概念,可研究几何相位 [11] [12] [13] [14] 与相应的与时间相关的薛定谔方程的精确解。Berry相位的发现不仅是旧的量子绝热近似理论的突破,也为我们提供了许多物理现象的新见解。Berry相位的概念已经发展到不同的方向 [15] - [27] 。基于Jaynes-Cummings模型 [28] - [33] 的研究,并通过使用Lewis-Riesenfeld不变量理论,我们将研究推广的含时二能级虚光子过程的Jaynes-Cummings模型中的几何相位。
2. 物理模型
推广的含时二能级虚光子过程的Jaynes-Cummings模型的哈密顿量为:
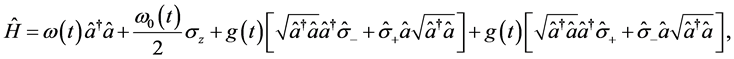 (1)
(1)
其中最后一项表示虚拟光子过程,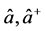 光表示光子的湮灭和产生算符。
光表示光子的湮灭和产生算符。
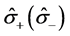 是定义为
是定义为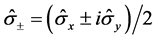 的原子的赝自旋律算符,
的原子的赝自旋律算符,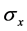 和
和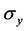 为Pauli矩阵,
为Pauli矩阵,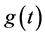 代表原子和光场之间的耦合强度,
代表原子和光场之间的耦合强度,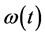 是电磁波的频率,
是电磁波的频率,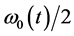 是单位
是单位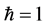 时原子的两个能级之间的能量差。
时原子的两个能级之间的能量差。
众所周知,假想的光子被原子以极快的速度吸收。如果我们使用更精确的设备,则可以观察该过程中的几何相位,这是本文的起点。基于这个想法,我们考虑以下系统的哈密顿算子:
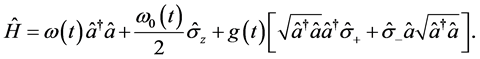 (2)
(2)
如果引入超对称生成元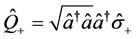 和
和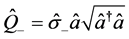
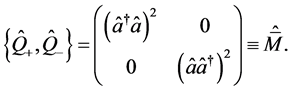 (3)
(3)
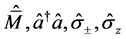 和
和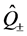 是超对称生成元,形成超对称Lie代数,即:
是超对称生成元,形成超对称Lie代数,即:
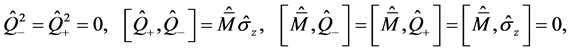 (4)
(4)
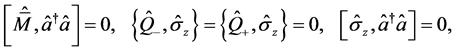 (5)
(5)
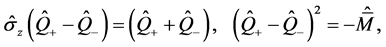 (6)
(6)
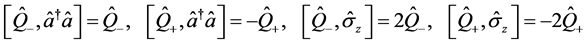 (7)
(7)
其中{,}代表反对易括号。方程(2)变为:
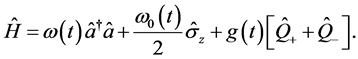 (8)
(8)
很容易发现:
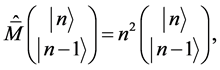 (9)
(9)
所以我们将研究限定在由运算符构成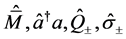 和
和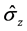 的代数的超对称的准希尔伯特空间下面,我们用特定的特征值
的代数的超对称的准希尔伯特空间下面,我们用特定的特征值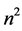 代替运算符
代替运算符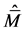 。
。
3. 动力学与几何相位
为了自洽,我们首先介绍Lewis-Riesenfeld (L-R)的不变理论 [10] ,对于与时间有关的一维哈密顿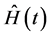 ,存在不变量量算符
,存在不变量量算符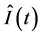 ,满足下式方程
,满足下式方程
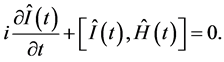 (10)
(10)
不变量满足特征值方程为
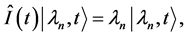 (11)
(11)
其中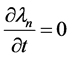 ,该系统的与时间有关的薛定谔方程为
,该系统的与时间有关的薛定谔方程为
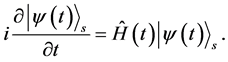 (12)
(12)
根据L-R不变理论,等式(12)的特定解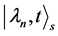 与
与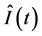 的本征函数
的本征函数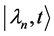 仅相位因子
仅相位因子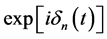 的不同,即,
的不同,即,
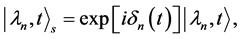 (13)
(13)
这表明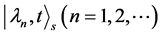 构成等式(12)解的完整集合。那么方程(12)的薛定谔方程的一般解可以写成
构成等式(12)解的完整集合。那么方程(12)的薛定谔方程的一般解可以写成
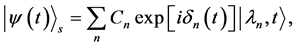 (14)
(14)
其中
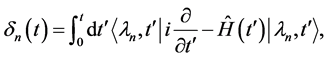 (15)
(15)
同时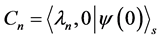 。
。
对于(8)式的哈密顿描述的系统,我们可以定义下面的不变量
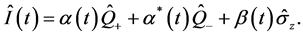 (16)
(16)
将方程(8)式和(16)式代入方程(10)式,得到一个辅助方程
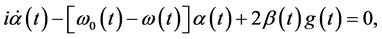 (17)
(17)
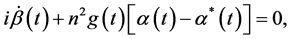 (18)
(18)
其中点表示对时间的导数。
为了获得与时间无关的不变量,我们可以引入单位变换算子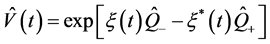 。当满足以下关系时,很容易得到
。当满足以下关系时,很容易得到
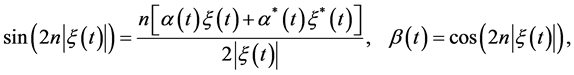 (19)
(19)
和
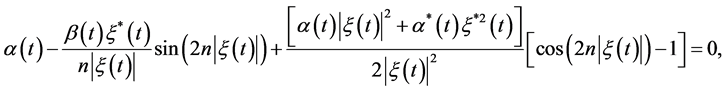 (20)
(20)
则可得到与时间无关的不变量
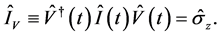 (21)
(21)
根据方程(19)式和(20)式,我们选择
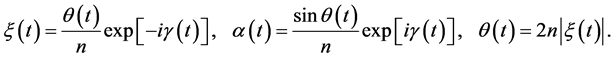 (22)
(22)
根据方程(22),方程(16)的不变量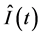 变为
变为
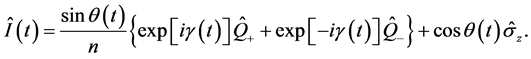 (23)
(23)
利用Baker-Campbell-Hausdoff公式 [34]
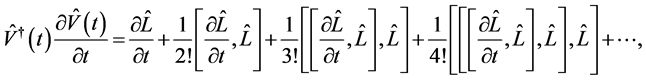 (24)
(24)
通过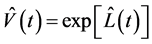 当满足下列等式时很容易得到
当满足下列等式时很容易得到
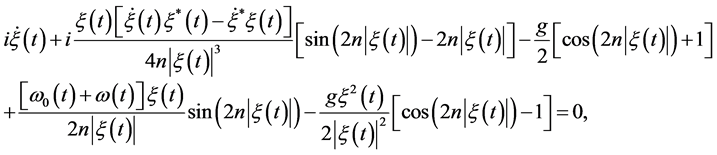 (25)
(25)
有
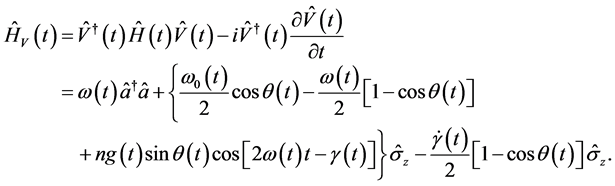 (26)
(26)
因此,我们可以分别获得方程(12)与时间有关的薛定谔方程的两个特定解。对于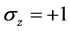
有
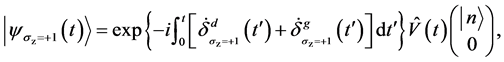 (27)
(27)
其中
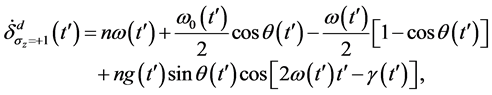 (28)
(28)
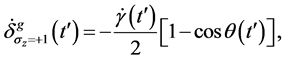 (29)
(29)
对于 ,
,
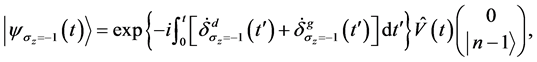 (30)
(30)
其中
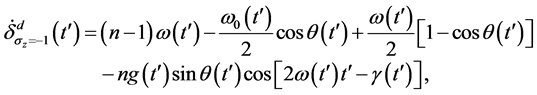 (31)
(31)
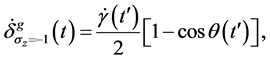 (32)
(32)
从等式(28)~(29)和(31)~(32),我们得出结论,当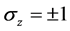 时,系统的动力学和几何相位因子分别为
时,系统的动力学和几何相位因子分别为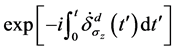 和
和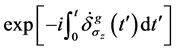 。特别是当我们考虑参数空间中循环时的一个不变量
。特别是当我们考虑参数空间中循环时的一个不变量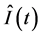 ,并且令
,并且令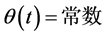 ,从式(29)和(32)得出
,从式(29)和(32)得出
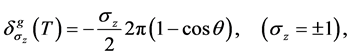 (33)
(33)
这里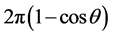 表示不变量
表示不变量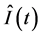 的参数空间上的立体角,这意味着几何相位代表了厄米线性束的整体 [35] 。
的参数空间上的立体角,这意味着几何相位代表了厄米线性束的整体 [35] 。
4. 结论
利用Lewis-Riesenfeld不变量理论,研究了推广的含时二能级虚光子过程的Jaynes-Cummings模型。发现周期情况下的几何相位与光子场的频率、光子和原子之间的耦合系数以及原子跃迁频率无关。
如果有更精确的设备,则可以观察到该虚拟光子过程中的几何相位,并且该过程中的几何相位具有可观察的物理效果。
基金项目
本文得到北京信息科技大学研究生院项目支持。
文章引用
乔元新,于肇贤. 虚光子过程中的几何相位
Geometric Phase in an Imaginary Photon Process[J]. 现代物理, 2017, 07(04): 148-154. http://dx.doi.org/10.12677/MP.2017.74016
参考文献 (References)
- 1. Pancharatnam, S. (1956) Generalized Theory of Interference, and Its Applications. Proceedings of the Indian Academy of Sciences—Section A, 44, 247-262.
- 2. Berry, M.V. (1984) Quantal Phase Factors Accompanying Adiabatic Changes. Proceedings of the Royal Society London, Series A, 392, 45. https://doi.org/10.1098/rspa.1984.0023
- 3. Aharonov, Y. and Anandan, J. (1987) Phase Change during a Cyclic Quantum Evolution. Physical Review Letters, 58, 1593. https://doi.org/10.1103/PhysRevLett.58.1593
- 4. Samuel, J. and Bhandari, R. (1988) General Setting for Berry’s Phase. Physical Review Letters, 60, 2339. https://doi.org/10.1103/PhysRevLett.60.2339
- 5. Mukunda, N. and Simon, R. (1933) Quantum Kinematic Approach to the Geometric Phase. I. General Formalism. Annals of Physics (N.Y.), 228, 205-268. https://doi.org/10.1006/aphy.1993.1093
- 6. Pati, A.K. (1995) Geometric Aspects of Noncyclic Quantum Evolutions. Physical Review A, 52, 2576. https://doi.org/10.1103/PhysRevA.52.2576
- 7. Uhlmann, A. (1986) Parallel Transport and “Quantum Holonomy” along Density Operators. Reports on Mathematical Physics, 24, 229-240. https://doi.org/10.1016/0034-4877(86)90055-8
- 8. Sjöqvist, E. (2000) Geometric Phases for Mixed States in Interferometry. Physical Review Letters, 85, 2845
- 9. Tong, D.M., et al. (2004) Kinematic Approach to the Mixed State Geometric Phase in Nonunitary Evolution. Physical Review Letters, 93, 080405. https://doi.org/10.1103/PhysRevLett.93.080405
- 10. Lewis, H.R. and Riesenfeld, W.B. (1969) An Exact Quantum Theory of the Time-Dependent Harmonic Oscillator and of a Charged Particle in a Time-Dependent Electromagnetic Field. Journal of Mathematical Physics, 10, 1458-1473. https://doi.org/10.1063/1.1664991
- 11. Gao, X.C., Xu, J.B. and Qian, T.Z. (1991) Geometric Phase and the Generalized Invariant Formulation. Physical Review A, 44, 7016. https://doi.org/10.1103/PhysRevA.44.7016
- 12. Gao, X.C., Fu, J. and Shen, J.Q. (2000) Quantum-Invariant Theory and the Evolution of a DIRAC FIELD in Friedmann-Robertson-Walker Flat Space-Times. European Journal of Physics, 13, 527-541. https://doi.org/10.1007/s100520000257
- 13. Gao, X.C., Gao, J., Qian, T.Z. and Xu, J.B. (1996) Quantum-Invariant Theory and the Evolution of a Quantum Scalar Field in Robertson-Walker Flat Spacetimes. Physical Review D, 53, 4374. https://doi.org/10.1103/PhysRevD.53.4374
- 14. Shen, J.Q. and Zhu, H.Y. (2003) arXiv: quant-ph/0305057v2
- 15. Richardson, D.J., et al. (1988) Demonstration of Berry's Phase Using Stored Ultracold Neutrons. Physical Review Letters, 61, 2030. https://doi.org/10.1103/PhysRevLett.61.2030
- 16. Wilczek, F. and Zee, A. (1984) Appearance of Gauge Structure in Simple Dynamical Systems. Physical Review Letters, 25, 2111. https://doi.org/10.1103/PhysRevLett.52.2111
- 17. Moody, J., et al. (1986) Realizations of Magnetic-Monopole Gauge Fields: Diatoms and Spin Precession. Physical Review Letters, 56, 893. https://doi.org/10.1103/PhysRevLett.56.893
- 18. Sun, C.P. (1990) Generalizing Born-Oppenheimer Approximations and Observable Effects of an Induced Gauge Field. Physical Review D, 41, 1349. https://doi.org/10.1103/PhysRevD.41.1349
- 19. Sun, C.P. (1993) Quantum Dynamical Model for Wave-Function Reduction in Classical and Macroscopic Limits. Physical Review A, 48, 898. https://doi.org/10.1103/PhysRevA.48.898
- 20. Sun, C.P. (1988) Flavor-Octet Dibaryons in the Quark Model. Physical Review D, 38, 298. https://doi.org/10.1103/PhysRevD.38.298
- 21. Sun, C.P., et al. (1988) High-Order Quantum Adiabatic Approximation and Berry's Phase Factor. Journal of Physics A, 21, 1595. https://doi.org/10.1088/0305-4470/21/7/023
- 22. Sun, C.P., et al. (2001) Quantum Measurement via Born-Oppenheimer Adiabatic Dynamics. Physical Review A, 63, Article ID: 012111. https://doi.org/10.1103/PhysRevA.63.012111
- 23. Chen, G., Li, J.Q. and Liang, J.Q. (2006) Critical Property of the Geometric Phase in the Dicke Model. Physical Review A, 74, Article ID: 054101. https://doi.org/10.1103/PhysRevA.74.054101
- 24. Chen, Z.D., Liang, J.Q., Shen, S.Q. and Xie, W.F. (2004) Dynamics and Berry Phase of Two-Species Bose-Einstein Condensates. Physical Review A, 69, Article ID: 023611. https://doi.org/10.1103/PhysRevA.69.023611
- 25. He, P.B., Sun, Q., Li, P., Shen, S.Q. and Liu, W.M. (2007) Magnetic Quantum Phase Transition of Cold Atoms in an Optical Lattice. Physical Review A, 76, Article ID: 043618. https://doi.org/10.1103/PhysRevA.76.043618
- 26. Li, Z.D., Li, Q.Y., Li, L. and Liu, W.M. (2007) Soliton Solution for the Spin Current in a Ferromagnetic Nanowire. Physical Review A, 76, Article ID: 026605. https://doi.org/10.1103/physreve.76.026605
- 27. Niu, Q., Wang, X.D., Kleinman, L., Liu, W.M., Nicholson, D.M.C. and Stocks, G.M. (1999) Adiabatic Dynamics of Local Spin Moments in Itinerant Magnets. Physical Review Letters, 83, 207. https://doi.org/10.1103/PhysRevLett.83.207
- 28. Jaynes, E.T. and Cummings, F.W. (1963) Comparison of Quantum and Semiclassical Radiation Theories with Application to the Beam Maser. Proceedings of the IEEE, 51, 89-109. https://doi.org/10.1109/PROC.1963.1664
- 29. Huang, H.B. and Fan, H.Y. (1991) Jaynes-Cummings Model for Double m-Photon Lasers. Physics Letters A, 159, 323-327. https://doi.org/10.1016/0375-9601(91)90441-A
- 30. Fan, H.Y. and Li, L.S. (1996) Supersymmetric Unitary Operator for Some Generalized Jaynes-Cummings Models. Communications in Theoretical Physics, 25, 105. https://doi.org/10.1088/0253-6102/25/1/105
- 31. Wu, Y. and Yang, X. (1997) Jaynes-Cummings Model for a Trapped Ion in Any Position of a Standing Wave. Physical Review Letters, 78, 3086. https://doi.org/10.1103/PhysRevLett.78.3086
- 32. Wu, Y. (1996) Simple Algebraic Method to Solve a Coupled-Channel Cavity QED Model. Physical Review A, 54, 4534. https://doi.org/10.1103/PhysRevA.54.4534
- 33. Wu, Y., Yang, Y.X., Wu, Y. and Li, Y.J. (1997) Unified and Standardized Procedure to Solve Various Nonlinear Jaynes-Cummings Models. Physical Review A, 55, 4545.
- 34. Wei, J. and Norman, E. (1963) Lie Algebraic Solution of Linear Differential Equations. Journal of Mathematical Physics, 4, 575. https://doi.org/10.1063/1.1703993
- 35. Simon, B. (1983) Holonomy, the Quantum Adiabatic Theorem, and Berry's Phase. Physical Review Letters, 51, 2167. https://doi.org/10.1103/PhysRevLett.51.2167