Advances in Geosciences
Vol.
13
No.
03
(
2023
), Article ID:
63184
,
12
pages
10.12677/AG.2023.133025
基于BP神经网络的Cole-Cole模型参数预测
岑海波1,罗润林1,李亚南1,冯彪1,汪芳2
1桂林理工大学地球科学学院,广西 桂林
2贵州医科大学药学院,贵州 贵阳
收稿日期:2023年2月15日;录用日期:2023年3月20日;发布日期:2023年3月28日

摘要
由于Cole-Cole模型的频谱参数可以用于区分引起激电异常的极化体和寻找深部矿(化)体,国内外学者采用复电阻率数据对频谱参数的确定做了大量的工作,并取得了很大的成果。而传统正演方法存在计算量大,面对复杂地形正演困难等,同时为了更好的准确识别矿体,减少误判。本文根据BP神经网络训练可直接通过输出预测值来代替传统正演算法,这可大大减少传统正演的时间,提高计算效率。预测结果验证了BP神经网络学习在理论上Cole-Cole模型参数反演是可行的、有效的,可为下一步的地球物理勘探工作提供更为丰富的参考价值及指导性意义。
关键词
频谱参数,Cole-Cole模型,BP神经网络,预测

Cole-Cole Model Parameter Prediction Based on BP Neural Network
Haibo Cen1, Runlin Luo1, Yanan Li1, Biao Feng1, Fang Wang2
1College of Earth Sciences, Guilin University of Technology, Guilin Guangxi
2College of Pharmacy, Guizhou Medical University, Guiyang Guizhou
Received: Feb. 15th, 2023; accepted: Mar. 20th, 2023; published: Mar. 28th, 2023

ABSTRACT
Since the spectral parameters of the Cole-Cole model can be used to distinguish polarizers that cause excitation anomalies and find deep ore bodies, scholars at home and abroad have done a lot of work on the determination of spectral parameters by using complex resistivity data, and have achieved great results. However, the traditional forward method has a large amount of calculation, and it is difficult to face complex terrain, and at the same time, in order to better accurately identify the ore body and reduce false judgment. According to BP neural network training, this paper can directly replace the traditional forward algorithm by outputting the predicted value, which can greatly reduce the time of traditional forward evolution and improve the computational efficiency. The prediction results verify that BP neural network learning is feasible and effective in theory for Cole-Cole model parameter inversion, which can provide richer reference value and guiding significance for the next geophysical exploration work.
Keywords:Spectrum Parameters, Cole-Cole Model, BP Neural Networks, Forecast

Copyright © 2023 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
激发极化法以不同岩、矿石在电流下的激电效应来寻找矿场的一种物探方法。它可分为频率域激发极化法和时间域激发极化法。它在地质构造探测,水文、岩土工程、环境地质调查等众多领域广泛应用。但常规激发极化法存在着难以区分与那些金属硫化物有相同物性产出的碳质、硫化物等非目标体和各种电磁耦合效应影响的两大难题。加上没有充分利用其中蕴含的信息,使得常规激发极化法的找矿效果受到了很大的影响。1978年,Pelton等 [1] 通过对岩(矿)石标本和露头的研究,证明Cole-Cole模型满足近似描述IP效应,模型中的4个参数:ρ0为电阻率;c为频率相关系数;m为充电率;τ为时间常数。随着不断深入研究,发现频谱参数在地球物理勘探中都具有重要意义。Pelton [1] ,Zonge [2] ,罗延钟 [3] 等发现不同的岩(矿)石具有不同的频谱参数特征,有无电磁耦合时的参数也同样存在差异;Major [4] ,吴之训 [5] ,Kemma [6] 等利用Cole-Cole模型频谱参数,有效区分出了引起激电异常的地质体,但认为其成败在于观测精度;随后Nordsiek [7] ,Grisseman [8] 等发现充电率 m可有效反映了可极化物质的含量,而可极化颗粒和孔隙大小都与时间常数τ有着密切关系;Revil [9] [10] ,Titov [11] 等研究发现岩(矿)石土中水的传导性、毛细管压力等都与频谱参数大小有关。在参数反演和真谱分解方面,罗延钟等 [3] 提出用视谱参数来确定真谱参数的解析计算方法;阮百尧和罗润林 [12] 提出只要四个频点数据就可求出模型参数的一种递推分解算法;Ghorbani [13] 提出贝叶斯模型对Cole-Cole模型反演,但反演实测数据效果不理想;随后他又提出对去除电磁耦合后的数据直接反演Cole-Cole模型参数的算法研究。罗润林等 [14] 采用最小二乘法从时域激电数据中反演出频谱参数信息,并实践中得到良好的效果。刘崧 [15] 对时域激电的一些案例分析和研究认为要解决诸如改进时域激电反演技术等问题。由于当前测量仪器的限制,在观测时间跨度大,观测时间变化无规律等问题上,很难做出相应改进。故充分利用时间常数信息可提高反演质量。
人工神经网络是1940年后出现的,它被认为是一种可行完全的非线性反演方法,故国内外地球物理工作者对此进行了大量研究。BP (Back Propagation)算法是人工神经网络中的一种监督式的学习算法。王鹤 [16] 等利用BP神经网络有效的提高了二维大地电磁的反演速度,但网络容易出现局部最优解。随后王鹤 [17] 又利用遗传算法对BP神经网络进行修改,并将反演结果跟最小二乘法反演对比,验证了遗传算法对二维大地电磁非线性反演的可行性和有效性。BP神经网络应用领域广泛,在自动控制、信号处理、医疗、经济和数据挖掘等领域,都取得较好的应用成果。本文基于MATLAB神经网络工具箱编写Cole-Cole模型参数训练与预测程序,探究了BP神经网络对Cole-Cole模型参数训练结果与预测效果的影响,最后确定了适合本文情况的BP神经网络训练预测的各项参数。用四组随机Cole-Cole模型参数样本训练和预测,预测结果验证了BP神经网络学习对于理论上Cole-Cole模型参数是可行的、有效的。
2. 原理
2.1. BP神经网络
BP神经网络是一种按误差逆传播算法训练的多层前馈神经网络。它是由众多的神经元可调的连接权值连接而成的,具有大规模并行处理、分布式信息存储、良好的自组织自学习能力等特点。其学习过程分为两个部分,第一部分是信号的前向传播,从输入层经过隐含层,再到达输出层;第二部分是误差的逆向传播,从输出层经过隐含层,再到输入层,依次调节隐含层到输出层的权重和偏置,输入层到隐含层的权重和偏置。
从图1看出,一个完整的BP神经网络模型由输入层、隐含层和输出层三部分组成。隐含层可以是一层或多层。图1是N × K × S的三层BP神经网络模型。输入层神经元个数与输入数据的维数相同,输出层神经元个数与需要拟合的数据个数相同,隐含层神经元个数与层数就需要自己根据一些规则和目标来设定。

Figure 1. Multilayer BP neural network model
图1. 多层BP神经网络模型
2.2. Cole-Cole模型的充电率正演计算
时间域激电视充电率mi定义为:
(1)
式(1)中:V0为供电时测量得到的一次场电位; 为第i个延时观测时段;V(t)为断电后t时刻的电位延时曲线。
根据时域中Cole-Cole模型的表达式,同时考虑D. Guptasarma [18] 数字滤波算法,即可以由式(1)计算出不同延时段的视充电率,得到式(4):
(2)
式中:I0为供电电流;Г(x)为伽马函数;ρ0为频率为零时的电阻率;c为频率相关系数;m为充电率;τ为时间常数。
3. BP神经网络训练与预测Cole-Cole模型参数
3.1. 训练集的参数选取
如表1所示。分别生成5000组,10,000组,20,000组和80,000组等四个样本集数据即分别为Ⅰ、Ⅱ、Ⅲ、Ⅳ组,由于c,m,τ都是随机取值故在得出的视充电率数据中可能存在一些较大异常值,需要对算出视充电率数据进行验证与处理。通过对数据归一化处理,可有效提升神经网络训练效率。
Table 1. Cole-Cole model spectrum parameter selection values
表1. Cole-Cole模型频谱参数选取值
本文设计了三种BP神经网络结构做对比,输入层的神经元节点为4,输出层的神经元节点为3,隐含层分别是单隐含层,双隐含层和三隐含层,其对应的神经元节点分别为 [12] ,[16,9],[8,16,12],即分别为4-[12]-3,4-[16,9]-3和4-[8,16,12]-3的神经网络结构。
3.2. 网络训练
由图2可发现5000组样本的BP神经网络训练预测反演结果形态基本一致。其中单隐含层BP神经网络结构预测c,m,τ对应的相关系数分别为0.57966,0.40077,0.92737,而均方误差损失函数(MSE)的值分别为0.00975,0.01821,0.18839,总均方误差损失函数(MSE)的值0.07212;双隐含层BP神经网络结构预测c,m,τ对应的相关系数分别为0.78055,0.42318,0.94492,而均方误差损失函数(MSE)的值分别为0.00864,0.01779,0.17494,总均方误差损失函数(MSE)的值0.06712;三隐含层BP神经网络结构预测c,m,τ对应的相关系数分别为0.78066,0.44937,0.95129,而均方误差损失函数(MSE)的值分别为0.00643,0.01541,0.13998,总均方误差损失函数(MSE)的值0.05394。表明BP神经网络训练Cole-Cole模型的5000组样本数据具有较高的精确度,数值接近,误差较小。


Figure 2. Schematic diagram of the parameter fitting effect of BP neural network training prediction model for 5000 sets of samples. (a) Single-hidden layer BP neural network structure training prediction parameters; (b) prediction parameters for structural training of double-hidden layer BP neural networks; (c) prediction parameters for structural training of BP neural networks in three hidden layers
图2. 5000组样本的BP神经网络训练预测模型参数拟合效果示意图。(a) 单隐含层BP神经网络结构训练预测参数;(b) 双隐含层BP神经网络结构训练预测参数;(c) 三隐含层BP神经网络结构训练预测参数
由图3可发现10000组样本的BP神经网络训练预测反演结果形态基本一致。其中单隐含层BP神经网络结构预测c,m,τ对应的相关系数分别为0.66055,0.41914,0.93884,而均方误差损失函数(MSE)的值分别为0.00684,0.01633,0.16642,总均方误差损失函数(MSE)的值0.06320;双隐含层BP神经网络结构预测c,m,τ对应的相关系数分别为0.71455,0.41914,0.94055,而均方误差损失函数(MSE)的值分别为0.00698,0.01626,0.17704,总均方误差损失函数(MSE)的值0.06676;三隐含层BP神经网络结构预测c,m,τ对应的相关系数分别为0.76923,0.52794,0.94372,而均方误差损失函数(MSE)的值分别为0.00601,0.01430,0.13935,总均方误差损失函数(MSE)的值0.05322。表明BP神经网络训练Cole-Cole模型的10000组样本数据具有较高的精确度,数值接近,误差较小。
从表2中可以看出,BP神经网络训练Cole-Cole模型参数c,m,τ的相关系数较高,均方误差损失函数(MSE)值较低,预测效果较好。对比三种不同BP神经网络结构训练预测结果可发现,使用三隐含层的BP神经网络结构,训练模型更加稳定,因此本文的预测反演精确度较高,误差较小,结果可靠。
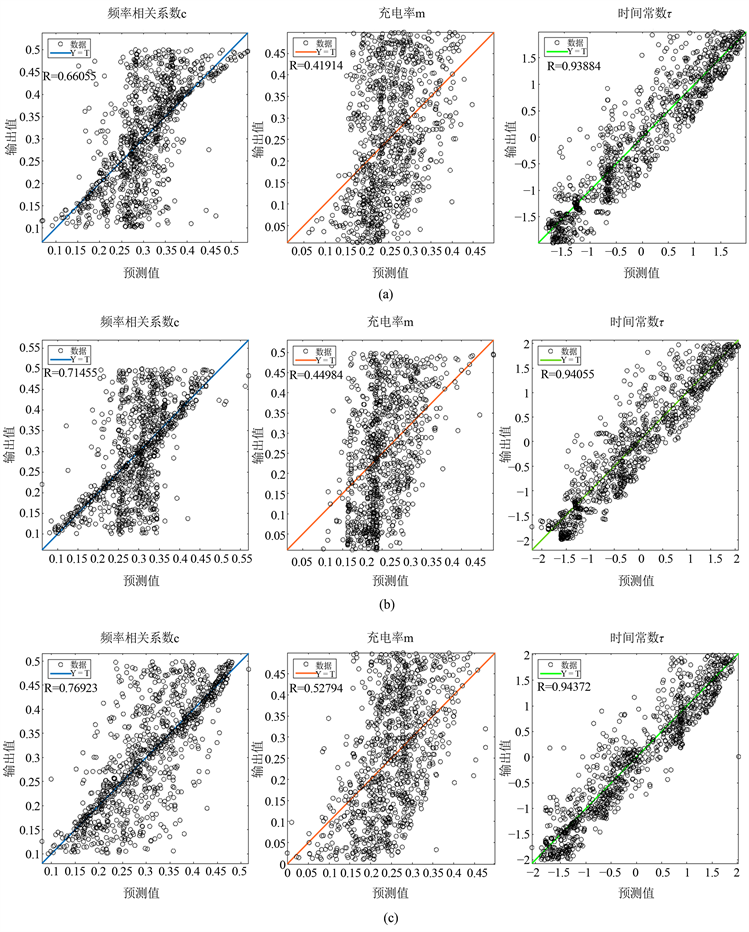
Figure 3. Schematic diagram of the parameter fitting effect of BP neural network training prediction model with 10000 sets of samples. (a) Single-hidden layer BP neural network structure training prediction parameters; (b) prediction parameters for structural training of double-hidden layer BP neural networks; (c) prediction parameters for structural training of BP neural networks in three hidden layers
图3. 10000组样本的BP神经网络训练预测模型参数拟合效果示意图。(a) 单隐含层BP神经网络结构训练预测参数;(b) 双隐含层BP神经网络结构训练预测参数;(c) 三隐含层BP神经网络结构训练预测参数
Table 2. BP neural network training Cole-Cole model correlation coefficient and mean squared error MSE
表2. BP神经网络训练Cole-Cole模型相关系数及均方误差MSE
3.3. 应用
图4为某矿区物探实际材料图。该区虽经多期构造运动作用,但次级褶皱不甚发育,而以大致平行地层走向的北东向断裂为主。多期次活动特点,派生、次级断裂发育,断裂多为压扭性、张性,是该区的矿液运移通道和储矿构造。该区构造运动频繁且强烈,岩浆作用多,褶皱断裂发育,变质作用强烈,是该区成矿的有利条件。
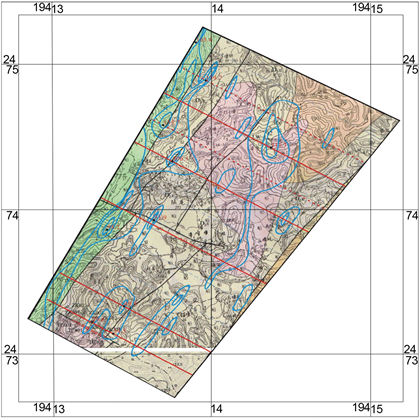
Figure 4. Actual material diagram of geophysical prospecting in a mining area
图4. 某矿区物探实际材料图
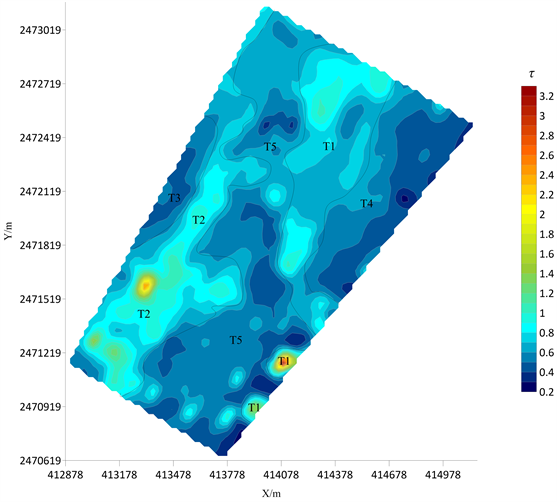
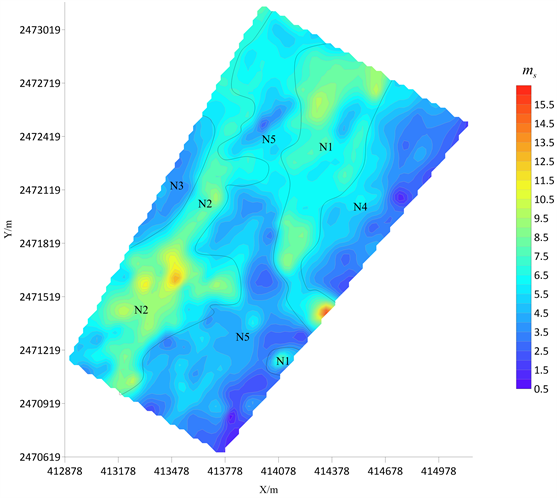
图5是该矿区实测数据代入BP神经网络中训练与预测结果图。应用Cole-Cole模型反演得到Cole-Cole模型参数后,可发现本测区频率相关系数c,充电率m,时间常数τ、视充电率ms和视电阻率ρs异常基本都呈带状分布,通过频谱参数对其进行划分,可划分为C1~C5的频率相关系数异常、M1~M5的充电率异常、T1~T5的时间常数异常和N1~N5的视充电率异常,由视电阻率可分为R1~R4的视电阻率异常。从图5可以看到C1、M1、T1、N1在同一异常为I异常,该异常位于测区北部,10线~23线中部,呈北东走向,视充电率大于5%,异常区域视电阻率值小于1000 Ω∙m,对应在R3低视电阻率异常带,属于低频率相关系数、高充电率、高时间常数、高视充电率、低阻异常带,可能是由黑云母花岗岩与围岩接触蚀变引起的,从异常的形态上,推测黑云母花岗岩体向北倾;C2、M2、T2、N2在同一异常为II异常,该异常位于测区西部,0线~23线西端,呈北东走向,视充电率大于6%,12线~23线西端异常区域视电阻率值大于1000 Ω∙m,对应R1的高视电阻率异常带,0线~11线西端异常区域视电阻率值小于600 Ω∙m,局部小于200 Ω∙m,在R3低视电阻率异常带内,属于低频率相关系数、高充电率、高时间常数、高视充电率异常带,可能为矿化引起的,推断断层向西倾;C3、M3、T3、N3在同一异常为III异常,该异常位于测区的西部,9线~17线最西端,视充电率小于5%,异常区域视电阻率值大于1000 Ω∙m,对应在R1的高视电阻率异常带,属于高频率相关系数、低充电率、低时间常数、低视充电率、高阻异常带,主要是花岗岩体及其与围岩接触变质等引起的;C4、M4、T4、N4在同一异常为IV异常,该异常带位于测区东部,11线~23线后部,呈北东走向,视充电率小于5%,异常区域视电阻率值大于1200 Ω∙m,局部大于2800 Ω∙m,对应在R2的高视电阻率异常带,属于高频率相关系数、低充电率、低时间常数、低视充电率、高阻异常带,可能是由黑云母花岗岩与围岩接触蚀变引起的;C5、M5、T5、N5在同一异常为V异常,该异常贯穿整个测区,呈北东走向,视充电率小于5%,其中0线~11线最东端异常带区域的视电阻率总体较低,一般小于600 Ω∙m,局部小于200 Ω∙m,在R4的低视电阻率异常带,正好与已知黄铁矿对应。而0线~11线的中部异常带区域的视电阻率值大于1200 Ω∙m,在R2高视电阻率异常带内,12线~23线的中东部异常区域视电阻率值小于800 Ω∙m,局部小于200 Ω∙m,在R3低视电阻率异常带内,该异常属于高频率相关系数、低充电率、低时间常数、低视充电率异常带。
 (a)
(a)
 (b)
(b)
 (c)
(c)
 (d)
(d)
 (e)
(e)
 (f)
(f)
Figure 5. The BP neural network on the mine area predicts and inverts the spectrum parameters of the Cole-Cole model. (a) Frequency correlation coefficient c; (b) charging rate m; (c) time constant τ; (d) depending on the charging rate ms; (e) apparent resistivity ρs; (f) estimation of the distribution of spectral parameters in the mining area
图5. 该矿区的BP神经网络预测反演Cole-Cole模型频谱参数。(a) 频率相关系数c;(b) 充电率m;(c) 时间常数τ;(d) 视充电率ms;(e) 视电阻率ρs;(f) 推测矿区频谱参数分布
4. 结论
1) 本文由视电阻率定义结合Cole-Cole模型表达式推导频谱参数并利用BP神经网络来代替传统正演算法,发现BP神经网络计算所需时间远少于传统正演算法计算时间,在训练与预测反演结果基本保持一致保持大体一致的情况下,能极大的减少用于反演计算的时间,提高效率优化反演。
2) 在对BP神经网络进行训练前需要对数据进行归一化处理,避免预测反演结果的均方误差损失函数过大,而影响反演精度。
3) 使用BP神经网络训练模型,需要多次设计不同隐含层和不同隐含层神经元节点数进行训练,才能确定适合训练该模型的隐含层参数。
4) 本文利用4个时间窗口的观测数据进行训练,预测反演Cole-Cole模型频谱参数的准确性可能不够高。若能获得更多时间窗口的观测数据,预测反演可能更好。
文章引用
岑海波,罗润林,李亚南,冯 彪,汪 芳. 基于BP神经网络的Cole-Cole模型参数预测
Cole-Cole Model Parameter Prediction Based on BP Neural Network[J]. 地球科学前沿, 2023, 13(03): 262-273. https://doi.org/10.12677/AG.2023.133025
参考文献
- 1. Pelton, W.H., Ward, S.H., Hallof, P.G., Sill, W.R. and Nelson, P.H. (1978) Mineral Discrimination and Removal of Inductive Coupling with Multifrequency IP. Geophysics, 43, 588-609. https://doi.org/10.1190/1.1440839
- 2. Zonge, K.L., Hughes, L.J. and Carlson, N.R. (1981) Hydrocarbon Ex-ploration Using Induced Polarization, Apparent Resistivity and Electromagnetic Scattering. 51st Annual International Meeting and Exposition SEG.
- 3. 罗延钟, 吴之训. 谱激电法中频率相关系数的应用[J]. 地球物理学报, 1992, 35(4): 490-500.
- 4. Major, J. and Silic, J. (1981) Restriction on the Use of Cole-Cole Dispersion Models in Complex Resistivity Interpretation. Geophysics, 46, 916-931. https://doi.org/10.1190/1.1441230
- 5. 吴之训. 频谱激电法在几个金属矿区的应用效果[J]. 物探与化探, 1987, 11(4): 281-290.
- 6. Kemna, A., Binley, A. and Slater, L. (2004) Crosshole IP Imaging for Engineering and Environmental Applications. Geophysics, 69, 97-107. https://doi.org/10.1190/1.1649379
- 7. Nordsiek, S. and Weller, A. (2008) A New Approach to Fitting In-duced-Polarization Spectra. Geophysics, 73, F235-F245.
- 8. Grissemann, C., Rammlmair, D., Siegwart, C. and Fouillet, N. (2000) Spectral Induced Polarization Linked to Image Analyses: A New Approach. In: Rammlmair, D., Mederer, J., Oberthür, T., Heimann, R. and Pentinghaus, H., Eds., Applied Mineralogy: Balkema, 561-564.
- 9. Revil, A. and Florsch, N. (2010) Determination of Permeability from Spectral Induced Polarization Data in Granular Media. Geophysical Journal International, 181, 1480-1498. https://doi.org/10.1111/j.1365-246X.2010.04573.x
- 10. Revil, A. and Skold, M. (2011) Salinity Dependence of Spectral Induced Polarization in Sands and Sandstones. Geophysical Journal International, 187, 813-824. https://doi.org/10.1111/j.1365-246X.2011.05181.x
- 11. Titov, K., Tarasov, A., Ilyin, Y., Seleznev, N. and Boyd, A. (2010) Relationships between Induced Polarization Relaxation Time and Hydraulic Properties of Sandstone. Geophysical Journal International, 180, 1095-1106. https://doi.org/10.1111/j.1365-246X.2009.04465.x
- 12. 阮百尧, 罗润林. 一种新的复电阻率频谱参数的递推反演方法[J]. 物探化探计算技术, 2003, 25(4): 298-301
- 13. Ghorbani, A., Camerlynck, C., Florsch, N., Cosenza, P. and Revil, A. (2007) Bayesian Inference of the Cole-Cole Parameters from Time- and Frequency Domain Induced Polarization. Geophysical Prospecting, 55, 589-605. https://doi.org/10.1111/j.1365-2478.2007.00627.x
- 14. 罗润林, 李亚南. 基于时域激电数据的Cole-Cole模型频谱参数反演[C]//中国地球物理学会. 第九届中国国际地球电磁学术讨论会论文集: 2009年卷. 桂林, 2009: 285-288.
- 15. 刘崧. 时间谱激电测量的可行性及值得研究的问题[J]. 地质科技情报, 1988, 7(1): 92-95.
- 16. 王鹤, 蒋欢, 王亮, 席振铢, 张道军. 大地电磁人工神经网络反演[J]. 中南大学学报(自然科学版), 2015, 46(5): 1707-1714.
- 17. 王鹤, 刘梦琳, 席振铢, 彭星亮, 何航. 基于遗传神经网络的大地电磁反演[J]. 地球物理学报, 2018, 61(4): 1563-1575.
- 18. Guptasarma, D. (1982) Computation of the Time-Domain Response of a Polarizable Ground. Geophysics, 47, 1574-1576. https://doi.org/10.1190/1.1441307
