Modeling and Simulation
Vol.05 No.04(2016), Article ID:19101,13
pages
10.12677/MOS.2016.54022
Synchronous Control on Wind Power Grid Inverter System with Nonlinear and Stochastic Noise Disturbance
Jiang Liu1, Long Zhang1, Zhongchuan Jiang2, Yanqing Li1
1Xinjiang University, Urumqi Xinjiang
2Goldwind Science & Technology Co., Ltd., Urumqi Xinjiang

Received: Nov. 9th, 2016; accepted: Nov. 26th, 2016; published: Nov. 29th, 2016
Copyright © 2016 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
Nonlinear circuits and systems are parts of nonlinear science, which have been central issues in various kinds of research fields. In this paper, we studied the synchronization control of wind power with disturbance of nonlinearity and white noise. By using the Kirchhoff’s law, we obtained the mathematical model of wind power grid side converter system. Meanwhile, an appropriate adaptive synchronization controller was designed. By establishing a suitable Lyapunov function, we validated the effectiveness of synchronous controller. Therefore, we can eliminate the disturbance of nonlinearity and white noise produced by the wind current embedding into the grid. As a result, we can make the current generated by the wind generator synchronize the current in the grid. Finally through Simulink in Matlab simulation, we validated our theoretical results.
Keywords:Nonlinear Perturbation, White Noise, Lyapunov Function, Synchronization, Itô Differential Formula

风电并网变流器系统中非线性和 随机噪声扰动的同步控制研究
刘江1,张龙1,蒋中川2,李艳青1
1新疆大学,新疆 乌鲁木齐
2金风科技股份有限公司,新疆 乌鲁木齐

收稿日期:2016年11月9日;录用日期:2016年11月26日;发布日期:2016年11月29日

摘 要
非线性电路与系统是非线性科学的一部分,目前以经受到各个领域的关注。本文研究了风力发电并网中带有随机白噪声和非线性扰动的同步控制问题。利用基尔霍夫定律得到了风力发电系统电网侧变流器的数学模型。设计了适当的自适应同步控制器,借助李雅普洛夫稳定性理论,验证了该同步控制器的有效性。进一步消除由于电流并网产生的非线性及随机扰动,使得风力发电机所产生的电流和电网所产生的电流同步。最后通过Matlab中的Simulink进行了仿真设计研究,验证了该理论结果的有效性。
关键词 :非线性扰动,随机白噪声,李雅普洛夫函数,同步,伊藤微分公式

1. 引言
近年来,风能作为一种绿色能源,在可再生能源领域得到了迅猛发展。随着风电装机容量占整个电力系统的比重逐渐增大,风电电能质量对电网的影响越来越受到关注 [1] 。非线性随机噪声对电流的扰动(又称谐波电流)是风力发电中普遍存在的一种现象,它在风力发电并网过程中一直扮演着重要的角色。关于并网过程中电流的非线性随机噪声扰动问题,已有学者对此做了有益的研究并提出了一些相应的控制方法 [2] [3] [4] [5] 。例如,针对并网矩阵变换器PWM信号开关频率较低,输出电流中谐波含量较大的问题,张小平,唐华平 [2] 等提出了并网变流器中采用T型滤波器取代传统的电感滤波器以抑制谐波电流。吴捷,柳明 [3] 结合电力系统的特性介绍了非线性在电力系统的具体应用,对多种非线性电力系统控制技术的基本原理进行了详细的介绍。姚骏,夏先锋 [4] 等在详细分析网侧变流器的谐波数学模型的基础上,提出一种抑制并网低次谐波电流分量的交叉耦合控制策略。但是上述控制方法都是从工程实用角度来解决谐波扰动问题,遗憾的是理论方面做得很少。本文在总结以上控制谐波电流优劣的基础上,提出了一种简便,可控性强的自适应控制器新方法,仿真结果表明在控制非线性随机噪声电流上效果很好。
风力发电变流器主要是由整流器和逆变器组成,变流器把发电机产生的正弦交流电转化为符合并入电网要求的正弦交流电,它的转化过程是由多组开关的开闭来完成的。下面以风力发电变流器部分将交流电转化为直流电原理为例进行分析电流随机扰动的部分由来:
图1中,a相代表图2中的第一相正弦交流电 ,b相代表图2中的第二相正弦交流电
,b相代表图2中的第二相正弦交流电 ,c相代表图2中的第三相正弦交流电
,c相代表图2中的第三相正弦交流电 ,当图2中的开关(1)和(4)闭合其它开关保持断开时,a相电流形成一个闭合回路电流,在a相电流到达a点时断开开关(1)和(4),同时闭合开关(3)和(6)其它开关保持断开,b相电流形成一个闭合回路电流,在b相电流到达b点时断开(3)和(6)开关,同时闭合开关(5)和(4),其它开关保持断开,c相电流形成一个闭合回路电流,在c相电流到达c点时,断开开关(5)和(4)。重复上述过程就可以把风机产生的交流电转化为直流电,且由图1知,交流电转化为直流电过程可以近似的看做线性过程。通过前面的分析可知,交流电转化为直流电过程的实质是由于三组开关组的不断切换所形成的,
,当图2中的开关(1)和(4)闭合其它开关保持断开时,a相电流形成一个闭合回路电流,在a相电流到达a点时断开开关(1)和(4),同时闭合开关(3)和(6)其它开关保持断开,b相电流形成一个闭合回路电流,在b相电流到达b点时断开(3)和(6)开关,同时闭合开关(5)和(4),其它开关保持断开,c相电流形成一个闭合回路电流,在c相电流到达c点时,断开开关(5)和(4)。重复上述过程就可以把风机产生的交流电转化为直流电,且由图1知,交流电转化为直流电过程可以近似的看做线性过程。通过前面的分析可知,交流电转化为直流电过程的实质是由于三组开关组的不断切换所形成的,
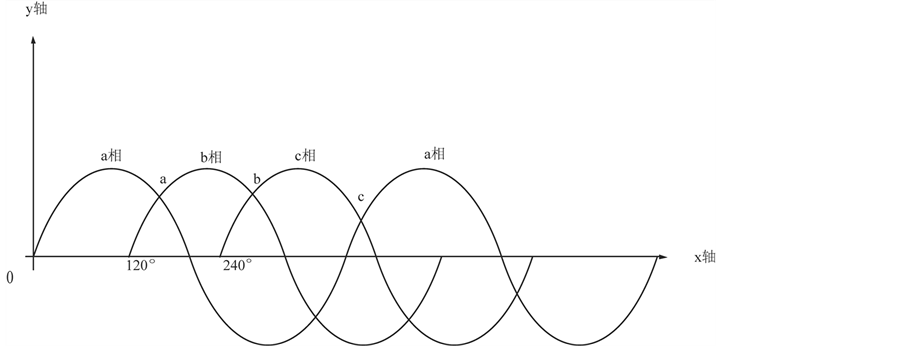
Figure 1. Three-phase sinusoidal alternating current
图1. 三相正弦交流电
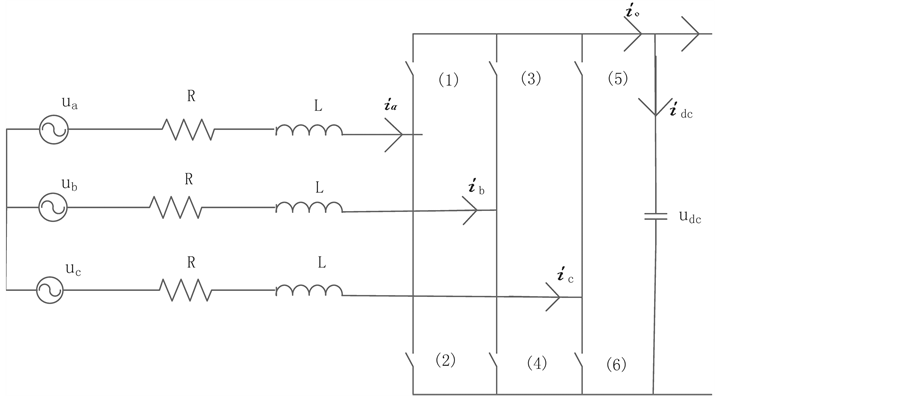
Figure 2. The grid side converter main circuit simplified model
图2. 电网侧变流器主电路简化模型
同理,整流器产生的直流电通过逆变器转化为交流电也是由三组开关组的不断切换所形成的,而在切换过程中会对整个电流传动系统造成许许多多细小的随机干扰,并且风机本身所处的外部环境也会对电流传动系统造成随机干扰,例如外界的电磁干扰等,这些干扰都可以用随机噪声扰动来描述。
电网侧变流器的主电路简化模型如图2所示。图中, 分别为电网三相电压。
分别为电网三相电压。 分别为电网三相电流。
分别为电网三相电流。 为直流侧电容电压。
为直流侧电容电压。 为直流侧电容电流。
为直流侧电容电流。 为电网侧变流器的并网电抗器的电阻及电感。
为电网侧变流器的并网电抗器的电阻及电感。
定义电网侧变流器开关函数为:
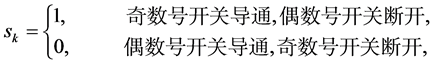 (1)
(1)
其中, 。
。
根据图2的电网侧变流器主电路简化模型,由基尔霍夫定律得到三相静止坐标系下电网侧变流器的高频数学模型 [6] :
 (2)
(2)
其中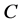 为直流侧电容,上述模型由于开关函数
为直流侧电容,上述模型由于开关函数 包括了其开关过程的高频分量,因而很难用于指导本文控制器的设计。假设本文开关频率远高于电网基波频率,为了简化数学模型,可忽略开关函数描述模型的高频分量,只考虑其中的低频分量,从而获得采用占空比描述的低频数学模型。这种采用占空比描述的低频变流器数学模型非常适合于控制系统分析,并且可直接用于控制器设计(通过傅里叶变换使得开关函数转化为对应的PWM占空比,其数学推导原理参考文献 [7] 的35页~36页)。
包括了其开关过程的高频分量,因而很难用于指导本文控制器的设计。假设本文开关频率远高于电网基波频率,为了简化数学模型,可忽略开关函数描述模型的高频分量,只考虑其中的低频分量,从而获得采用占空比描述的低频数学模型。这种采用占空比描述的低频变流器数学模型非常适合于控制系统分析,并且可直接用于控制器设计(通过傅里叶变换使得开关函数转化为对应的PWM占空比,其数学推导原理参考文献 [7] 的35页~36页)。
为了便于控制系统的设计,将模型(2)由三相静止坐标系转换到两相静止坐标系,可以得到两相静止坐标系下的变流器数学模型 [8] :
 (3)
(3)
此模型中 为两相静止坐标系下
为两相静止坐标系下 轴,
轴, 轴电流。
轴电流。 和
和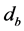 为静止坐标系下占空比
为静止坐标系下占空比 轴分量和
轴分量和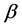 轴分量且
轴分量且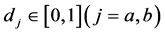 [7] 。
[7] 。
由于风速受天气变化的影响而表现出很强的非线性、非平稳性、随机性和不确定性使得风电系统电流的非线性动态特征与常规电力系统相比会更加明显。风机在发电过程所产生非线性动态特征加剧了风电场中所产生电流的不稳定性,随着风电在整个国家电网中所占比重越来越大,其对电网的影响也随之增强。如果一个发电功率较大的风电场发生非线性扰动,这种场级的非线性扰动会对整个电网造成很大的冲击,因此采取合适的方法对风电系统复杂震荡现象进行研究是十分必要的。因为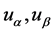 在并网系统中可测量,故本文可采用对电网的三相电压源每一相并联一个蔡式二极管 [9] (如图3所示),故有
在并网系统中可测量,故本文可采用对电网的三相电压源每一相并联一个蔡式二极管 [9] (如图3所示),故有 ,用此来模拟电网侧电流由于受到外界干扰而产生的非线性动态特征。
,用此来模拟电网侧电流由于受到外界干扰而产生的非线性动态特征。
图3为带有非线性扰动的电网侧变流器模型,则模型(3)变为:
 (4)
(4)
这里:

其中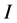 ,
, ,
,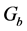 为蔡式二极管的典型参数(已知量)。令
为蔡式二极管的典型参数(已知量)。令 ,
,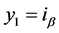 ,
, 模型(4)可以得到简化。
模型(4)可以得到简化。
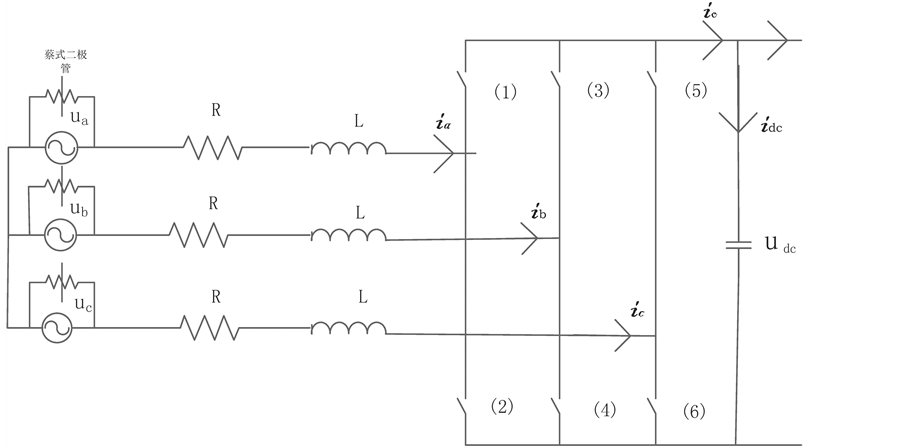
Figure 3. Simplified model with nonlinear disturbance in the grid side converter main circuit
图3. 带有非线性扰动电网侧变流器主电路简化模型
令:
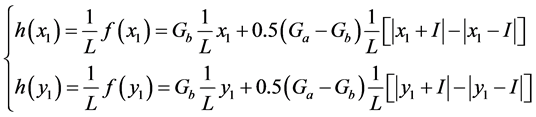
再令 ,
, ,将
,将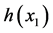 分三段来考虑,则有:
分三段来考虑,则有:
 (6)
(6)
2. 预备知识
定义1 [10] :如果存在常数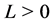 ,使得对任意
,使得对任意 都有
都有 ,则称
,则称 在R上关于
在R上关于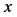 满足Lipschitz条件,常数L称为Lipschitz常数。
满足Lipschitz条件,常数L称为Lipschitz常数。
令矩阵:

因为R,L,C在变流器传动部分是可以取定为已知常数,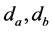 在[0,1]中取值也可以把它视作常数部分,故a,b,c,d,e,f都可以做为已知量。
在[0,1]中取值也可以把它视作常数部分,故a,b,c,d,e,f都可以做为已知量。
整理两相静止坐标系下的变流器数学模型如下:
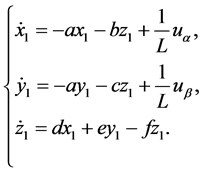 (7)
(7)
显然系统(7)是没有受到扰动的交流电数学模型,把它做为驱动系统。为了得到同步,我们构造带有非线性扰动的响应系统模型如下:
 (8)
(8)
其中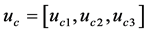 是同步控制器,由于驱动系统(7)和响应系统(8)的电路结构不同,故加入结构补偿器
是同步控制器,由于驱动系统(7)和响应系统(8)的电路结构不同,故加入结构补偿器 [11] 保证这两个系统的电路结构相同。
[11] 保证这两个系统的电路结构相同。
为证明带有非线性扰动的响应系统(8)和没有受到扰动的驱动系统(7)同步,我们引入如下定义:
定义2 [12] :对驱动系统(7)和响应系统(8),如果对任意初始状态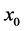 和
和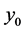 满足:
满足:

则称驱动系统(7)和响应系统(8)是同步的。
由引言,我们知道风力发电在传动部分对电流产生的噪声扰动原理,它的实质是由于多组开关组的闭合与断开以及外界环境对电流扰动所造成的。下面这一部分我们将进一步考虑风力发电并网系统在变流过程中,由于变流器部分对整个并入电网系统的交流电所造成的许许多多细小的、独立的随机干扰。因为响应系统(8)的前两个方程是未受到整流的交变电流,第三个方程是整流后稳定的直流电流,故把噪声扰动加到响应系统(8)的前两个方程是合理的,则驱动系统和带有非线性噪声扰动的响应系统方程分别如下:
 (10)
(10)
和
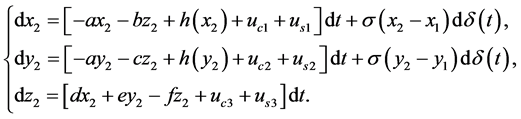 (11)
(11)
中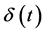 是一维布朗运动,且满足
是一维布朗运动,且满足 ,这里
,这里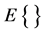 是数学期望,并且
是数学期望,并且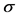 是噪声强度。为了方便噪声扰动部分产生误差项,假设响应系统
是噪声强度。为了方便噪声扰动部分产生误差项,假设响应系统 ,
, 电流强度远大于驱动系统中
电流强度远大于驱动系统中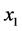 ,
,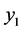 电流强度,则响应系统中
电流强度,则响应系统中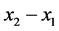 ,
, 可以近似等于
可以近似等于 ,
,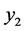 。可以用
。可以用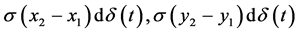 近似刻画变流器中开关组不断切换和外部环境等原因对正弦电流
近似刻画变流器中开关组不断切换和外部环境等原因对正弦电流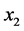 和
和 造成的噪声扰动。
造成的噪声扰动。
为证明带有非线性噪声扰动的响应系统(11)和没有受到扰动的驱动系统(10)同步,我们引入如下定义及引理:
定义4 [13] :对主要结果中的驱动系统(10)和响应系统(11),如果对任意初始状态 和
和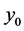 满足:
满足:
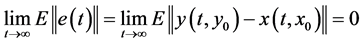
称误差系统的一般解在均方下是渐近稳定的,并称驱动系统(10)和响应系统(11)是同步的。
3. 主要结果
下面这一部分将使用合适的控制策略去设计线性自适应同步控制器,保证响应系统和驱动系统之间同步。
针对驱动系统(8)和响应系统(7),定义误差变量 ,则用受到非线性扰动的驱动系统(8)和没有受到扰动的响应系统(7)做差可得到误差系统模型为:
,则用受到非线性扰动的驱动系统(8)和没有受到扰动的响应系统(7)做差可得到误差系统模型为:
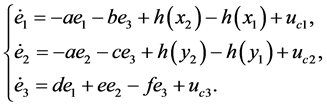 (9)
(9)
其中取定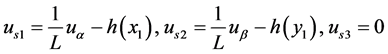 。在线性控制器的控制作用下,若能使得
。在线性控制器的控制作用下,若能使得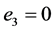
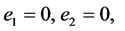 则表明受到非线性扰动的驱动系统(8)和没有受到扰动的响应系统(7)达到同步,即电流的非线性扰动被消除。
则表明受到非线性扰动的驱动系统(8)和没有受到扰动的响应系统(7)达到同步,即电流的非线性扰动被消除。
定理1:驱动系统(7)和响应系统(8)在自适应控制器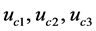 下是同步的,其中:
下是同步的,其中:
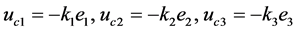 。
。
证明:取定Lyapunov函数: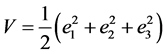 ,则有:
,则有:
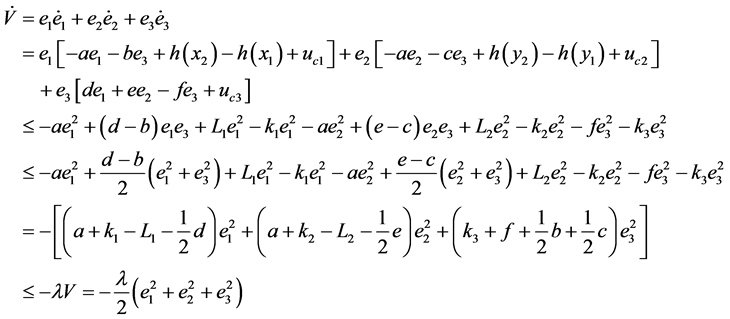
即有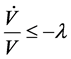 ,对该不等式两边同时关于
,对该不等式两边同时关于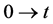 积分后得到
积分后得到 ,又
,又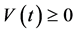 ,当
,当 时易知
时易知 ,因此
,因此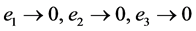 。则驱动系统(7)和响应系统(8)是同步的。
。则驱动系统(7)和响应系统(8)是同步的。
其中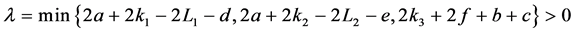 ,同时由Lagrange中值定理知:
,同时由Lagrange中值定理知: ,可取
,可取 ,
,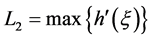 ,故
,故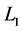 ,
, 可以得到具体数值。在取定合适的
可以得到具体数值。在取定合适的 值,综上所述可以得到自适应控制器
值,综上所述可以得到自适应控制器 的数值,则定理1证明完毕。
的数值,则定理1证明完毕。
针对驱动系统(10)和响应系统(11),定义误差变量 ,则响应系统(11)和驱动系统(10)做差可得到误差系统模型为:
,则响应系统(11)和驱动系统(10)做差可得到误差系统模型为:
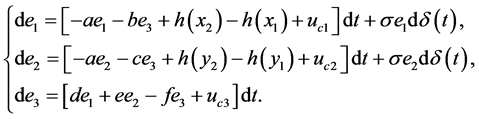 (12)
(12)
取定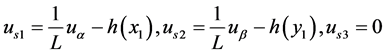 。若能使得
。若能使得 则表明受到非线性噪声扰动的响应系统(11)将趋近与没有受到扰动的驱动系统(10),即表明非线性扰动噪声扰动被消除。
则表明受到非线性噪声扰动的响应系统(11)将趋近与没有受到扰动的驱动系统(10),即表明非线性扰动噪声扰动被消除。
定理2:如果设计下面三个线性自适应反馈控制器:

则驱动系统(10)和响应系统(11)在以上自适应控制器下是同步的,这里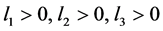 是任意的常数。
是任意的常数。
证明:取Lyapunov函数:

这里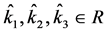 为待定常数。
为待定常数。
通过伊藤微分公式 [14] 有:
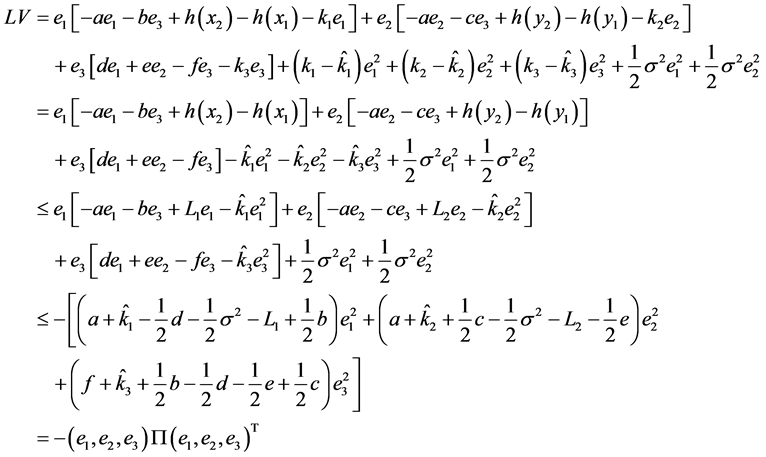 ,
,
其中

取定合适的 ,使
,使 保持正定,则有:
保持正定,则有:
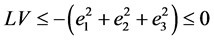
基于随机拉萨尔不变原理 [15] ,我们有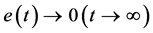 ,即意味着存在初值
,即意味着存在初值 使得
使得 ,同时有:
,同时有: (常数),则定理得证。
(常数),则定理得证。
更进一步,由于第三个方程代表的是变流器直流侧的方程,通常情况下我们可以不用考虑它所受到扰动,故有:
推论2:如果设计有下面三个线性自适应反馈控制器:

则驱动系统(10)和响应系统(11)在以上自适应控制器下是同步的,这里 是任意的常数。
是任意的常数。
4. 仿真及实验验证
根据前面所描述的电网侧电流方程以及非线性和非线性噪声扰动电流方程的表达式,有如下框图。如图4所示,假设我们从变流器和电网之间引入A,B,C三相标准正弦交流电,在通过扰动模块后,正弦交流电就变为现实中从变流器出来的有扰动电流,为了便于自适应控制器的设计,本文把有扰动的三相静止交流电转化为有扰动的两相静止交流电。有扰动的两相静止交流电在通过文中所设计的自适应控制器作用转变为无扰动的交流电,最后通过三相静止到两相静止的逆变换过程转化为正常的三相正弦交流电并入电网。
为了验证上述控制策略的有效性,下面使用Matlab/Simulink以两相静止坐标系下的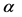 轴正弦交流电为例进行仿真研究。通过文中对带有非线性结构扰动情况的说明以及结合定理1,在Simulink上搭建了符合消除带有非线性电流扰动的模型,把模型分为了两部分A:
轴正弦交流电为例进行仿真研究。通过文中对带有非线性结构扰动情况的说明以及结合定理1,在Simulink上搭建了符合消除带有非线性电流扰动的模型,把模型分为了两部分A: 轴扰动交流电部分模拟图4中
轴扰动交流电部分模拟图4中 轴扰动电流和B:控制器部分模拟图4中控制器,模型如图5所示。由于大多数非线性系统都可以化分为线性部分和非线性部分串联而成的系统,故把
轴扰动电流和B:控制器部分模拟图4中控制器,模型如图5所示。由于大多数非线性系统都可以化分为线性部分和非线性部分串联而成的系统,故把 轴电流方程分为线性部分和非线性部分,线性部分以
轴电流方程分为线性部分和非线性部分,线性部分以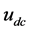 为输入量,
为输入量,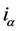 为输出量用拉普拉斯变换得到了线性部分的传递函数(如图5中的T)。并以自动控制原理非线性控制系统中的描述函数法 [16] 为基础得到了非线性部分的传递函数。我们在Simulink上设计了如图6所示的蔡氏二极管非线性扰动模型(图5中的非线性扰动模块为图6的封装模块),图6为正弦波通过非线性扰动模块后得到的开关式非线性正弦交流电波形图。观察图7可知:交流电波形符合蔡式二极管对正弦交流电扰动的非线性结构特点,显然这样的交流电不符合并入电网交流电的要求。
为输出量用拉普拉斯变换得到了线性部分的传递函数(如图5中的T)。并以自动控制原理非线性控制系统中的描述函数法 [16] 为基础得到了非线性部分的传递函数。我们在Simulink上设计了如图6所示的蔡氏二极管非线性扰动模型(图5中的非线性扰动模块为图6的封装模块),图6为正弦波通过非线性扰动模块后得到的开关式非线性正弦交流电波形图。观察图7可知:交流电波形符合蔡式二极管对正弦交流电扰动的非线性结构特点,显然这样的交流电不符合并入电网交流电的要求。
结合定理1知:在满足 和
和 的具体数值后,可以计算出控制器
的具体数值后,可以计算出控制器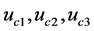 控制住扰动的取值,取定
控制住扰动的取值,取定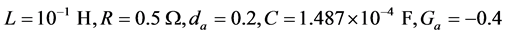 ,有
,有 轴交流电控制器参数取值范围
轴交流电控制器参数取值范围 ,取定
,取定 ,把所得数值代入图7的增益控制器并在Simulink上运行图7模型后得
,把所得数值代入图7的增益控制器并在Simulink上运行图7模型后得

Figure 4. Grid side current disturbance control diagram mode
图4. 电网侧电流扰动控制框图模型

Figure 5. Control diagram model of nonlinear disturbance
图5. 非线性扰动的控制框图模型

Figure 6. Nonlinear structural diagram model
图6. 非线性结构框图模型

Figure 7. Alternating current (ac) of nonlinear disturbance
图7. 非线性扰动的交流电
到的波形如图8中图B所示,通过图B可以看出在线性控制器的作用下误差系统渐近收敛到0,即有非线性扰动的交流电趋近于无非线性噪声扰动的交流电,从而消除了电流中的非线性扰动。
图8中图A表示的是图7中标准正弦交流电(即没有受到扰动的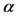 轴标准正弦交流电波形),图B表示正弦交流电受到非线性扰动后经过控制器控制后所得到的交流电波形。通过图8可以看出,两者的幅值和相角都完全一样,因此由定理1所设计的控制器可以控制住如图6所示受到非线性扰动的交流电,使得它恢复正常从而使并入电网的电流健康,不会对电网造成影响。同理控制
轴标准正弦交流电波形),图B表示正弦交流电受到非线性扰动后经过控制器控制后所得到的交流电波形。通过图8可以看出,两者的幅值和相角都完全一样,因此由定理1所设计的控制器可以控制住如图6所示受到非线性扰动的交流电,使得它恢复正常从而使并入电网的电流健康,不会对电网造成影响。同理控制 轴正弦交流电,最后把得到无扰动的
轴正弦交流电,最后把得到无扰动的 和
和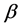 轴正弦交流电通过两相静止交流电转化为三相静止交流电模块转化为三相交流电,然后再并入电网。
轴正弦交流电通过两相静止交流电转化为三相静止交流电模块转化为三相交流电,然后再并入电网。
下面对带有非线性随机噪声扰动电流的仿真,通过前面对该问题的描述以及定理2的证明,在Simulink上搭建了符合消除带有随机白噪声的非线性电路扰动方框,同理把模型分为了两部分A: 轴正弦扰动交流电部分模拟图4中
轴正弦扰动交流电部分模拟图4中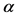 轴扰动电流和B:控制器部分模拟图4中控制器。模型如图9所示。
轴扰动电流和B:控制器部分模拟图4中控制器。模型如图9所示。
图10和图11是在不同的 噪声强度条件下在Simulink上运行了图9模型后,用示波器在A部分测的有扰动交流电波形图,由图像分析可知交流电波形不仅受到非线性扰动还受到变流器和外界环境的噪声扰动,在不同的噪声强度下交流电所受到的扰动强弱也不同,显然这样的电流也是不符合并入电网要求的。
噪声强度条件下在Simulink上运行了图9模型后,用示波器在A部分测的有扰动交流电波形图,由图像分析可知交流电波形不仅受到非线性扰动还受到变流器和外界环境的噪声扰动,在不同的噪声强度下交流电所受到的扰动强弱也不同,显然这样的电流也是不符合并入电网要求的。
取定噪声强度 (如图10所示),驱动系统和响应系统的初值为
(如图10所示),驱动系统和响应系统的初值为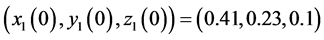 和
和 。根据定理2的证明,我们知道当
。根据定理2的证明,我们知道当 ,
,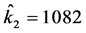 ,
,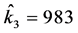
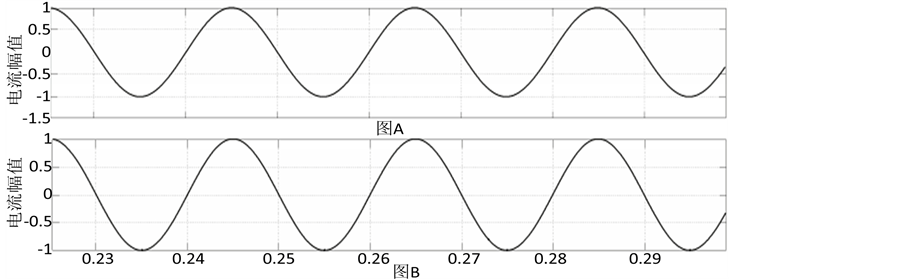
Figure 8. Alternating current waveform figure
图8. 交流电对比波形图
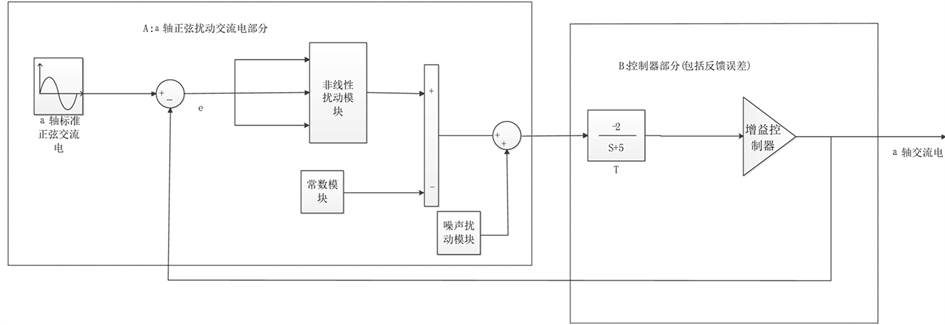
Figure 9. Nonlinear control diagram of the disturbance of noise model
图9. 非线性噪声扰动的控制框图模型
时有 ,非线性随机噪声同步能够被实现。当反馈增益控制器的初值是
,非线性随机噪声同步能够被实现。当反馈增益控制器的初值是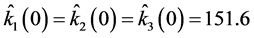 并且
并且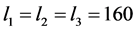 时,同样以
时,同样以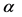 轴电流为例,当
轴电流为例,当 轴电流的控制器参数取定为
轴电流的控制器参数取定为 时,把该数值带入图10非线性噪声扰动的控制框图模型中的增益控制器模块并在Simulink上运行后得到图12中的图C,通过图C显然可以看出在线性控制器的作用下误差系统渐近收敛到0,即有非线性噪声扰动的交流电趋近于无非线性噪声扰动的交流电。从而消除了非线性噪声扰动,同时反馈增益将很快趋近于一个固定常数。
时,把该数值带入图10非线性噪声扰动的控制框图模型中的增益控制器模块并在Simulink上运行后得到图12中的图C,通过图C显然可以看出在线性控制器的作用下误差系统渐近收敛到0,即有非线性噪声扰动的交流电趋近于无非线性噪声扰动的交流电。从而消除了非线性噪声扰动,同时反馈增益将很快趋近于一个固定常数。
图D表示的是图9中标准正弦交流电(即没有受到扰动的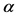 轴标准正弦交流电波形),对比图12可知这两个波形图的幅值和相角都完全一样,因此由定理2所设计的控制器可以控制住非线性噪声扰动的交流电,使得带有扰动的交流电和正常的交流电之间达到同步。同理控制
轴标准正弦交流电波形),对比图12可知这两个波形图的幅值和相角都完全一样,因此由定理2所设计的控制器可以控制住非线性噪声扰动的交流电,使得带有扰动的交流电和正常的交流电之间达到同步。同理控制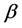 轴正弦交流电,最后把得到无扰动的
轴正弦交流电,最后把得到无扰动的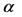 和
和 轴正弦交流电通过两相静止交流电转化为三相静止交流电模块转化为三相交流电,然后并入电网。
轴正弦交流电通过两相静止交流电转化为三相静止交流电模块转化为三相交流电,然后并入电网。
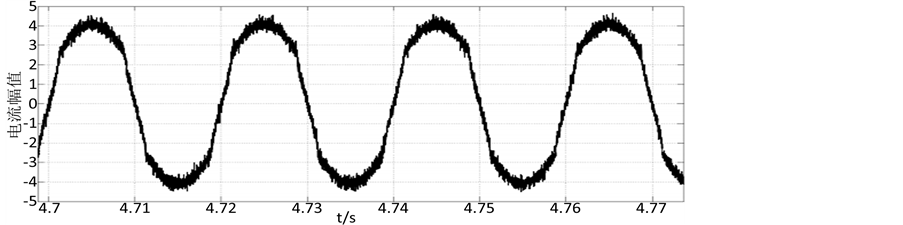
Figure 10. The nonlinear noise disturbance of noise intensity σ = 0.05 alternating current waveform figure
图10. 噪声强度σ = 0.05的非线性噪声扰动交流电波形图
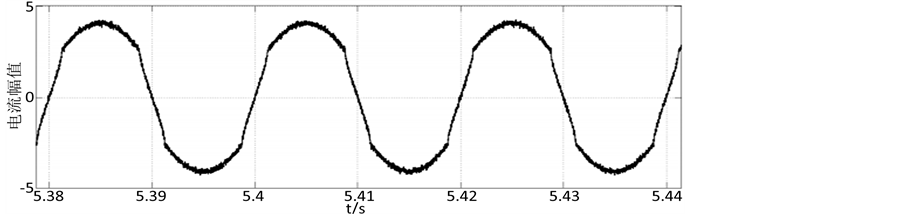
Figure 11. The nonlinear noise disturbance of noise intensity σ = 0.012 alternating current waveform figure
图11. 噪声强度σ = 0.012的非线性噪声扰动交流电波形图

Figure 12. Alternating current waveform figure
图12. 交流电对比波形图
5. 结论
本文通过对风力发电并网中带有非线性噪声扰动并网电流问题的研究,建立了基于电网侧变换器主电路微分方程的非线性噪声扰动模型,为了消除电流非线性噪声扰动,构造了误差系统,设计了适当的自适应同步控制器,借助李雅普洛夫稳定性理论给出了控制器的准确算法,并在Matlab中的Simulink上进行了仿真设计研究证明了该算法的有效性。
基金项目
国家自然科学基金(11361059, 11271312);新疆科技青年创新人才发展项目(2014721014);新疆高校科研项目(XJEDU2013I03)。
文章引用
刘江,张龙,蒋中川,李艳青. 风电并网变流器系统中非线性和随机噪声扰动的同步控制研究
Synchronous Control on Wind Power Grid Inverter System with Nonlinear and Stochastic Noise Disturbance[J]. 建模与仿真, 2016, 05(04): 170-182. http://dx.doi.org/10.12677/MOS.2016.54022
参考文献 (References)
- 1. Sainz, L., Mesas, J., Teodorescu, R. and Rodriguez, P. (2010) Deterministic and Stochastic Study of Wind Farm Harmonic Currents. IEEE Transactions on Energy Conversion, 25, 1071-1080. https://doi.org/10.1109/TEC.2010.2045379
- 2. 张小平, 唐华平, 朱建林, 李白燕. 并网矩阵变换器网侧谐波及稳定性分析[J]. 太阳能学报, 2007, 28(1): 431- 437.
- 3. 吴捷, 柳明. 非线性控制在电力系统中的应用[J]. 控制理论与应用, 2002, 19(1): 1000-8152.
- 4. 姚骏, 夏先锋, 陈西寅, 廖勇. 风电并网用全功率变流器谐波电流抑制研究[J]. 中国电机工程学报, 2012, 32(16): 470-476.
- 5. Sun, Z.Q., Chen, C.Z. and Liang, S.M. (2012) Fault Diagnosis for Large-Scale Wind Turbines. Applied Mechanics and Materials, 210-223, 740-743. https://doi.org/10.4028/www.scientific.net/AMM.220-223.740
- 6. 庄凯, 廖勇. 直驱式永磁风力发电机组并网变换器关键技术研究[D]: [博士学位论文]. 重庆: 重庆大学, 2012.
- 7. 张兴, 张崇巍. PWM整流器及其控制策略的研究[D]: [博士学位论文]. 合肥: 合肥工业大学, 2003.
- 8. 祝贺, 徐建源. 直驱式永磁风力发电机组数学模型及并网运行特性研究[D]: [博士学位论文]. 沈阳: 沈阳工业大学, 2013.
- 9. 杨志民, 张洁, 马永杰, 摆玉龙, 马胜前. 基于电流传输器的蔡氏混沌电路的设计和实现[J]. 物理学报, 2010, 59(5): 1000-3290.
- 10. Fang, S.Z., Imkeller, P. and Zhang, T.S. (2007) Global Flows for Stochastic Differential Equations without Global Lipschitz Conditions. The Annals of Probability, 35, 180-205. https://doi.org/10.1214/009117906000000412
- 11. 牛弘, 张国山. 混沌及超混沌系统的分析、控制、同步与电路实现[D]: [博士学位论文]. 天津: 天津大学, 2014.
- 12. Zhu, H., Zhou, S.B. and Zhang, J. (2007) Chaos and Synchronization of the Fractional-Order Chua’s System. Chaos, Solitons & Fractals, 21, 120-135.
- 13. Sun, Y.H. and Cao, J.D. (2007) Adaptive Synchronization between Two Different Noise-Perturbed Chaotic Systems with Fully Unknown Parameters. Physica A: Statistical Mechanics and its Applications, 376, 253-265. https://doi.org/10.1016/j.physa.2006.10.039
- 14. Friedman (1976) Stochastic Differential Equations and Applications. Academic Press, New York.
- 15. Mao, X.R. (2002) A Note on the LaSalle-Type Theorems for Stochastic Differential Delay Equations. Journal of Mathematical Analysis and Applications, 268, 125-142. https://doi.org/10.1006/jmaa.2001.7803
- 16. 胡寿松. 自动控制原理[M]. 第六版. 北京: 科学出版社, 2013: 382-399.