Statistics and Application
Vol.05 No.04(2016), Article ID:19335,7
pages
10.12677/SA.2016.54040
Government Revenue Forecast Based on Big Data Technology
—Taking Guizhou Province as an Example
Man Luo, Qun Wang, Yiling Yang, Junlei Mei
Guizhou Education University, Guiyang Guizhou

Received: Nov. 29th, 2016; accepted: Dec. 12th, 2016; published: Dec. 23rd, 2016
Copyright © 2016 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
In this paper, combined with the content and the structure characteristics of fiscal revenue in Guizhou, using the R software, the data were collected and analyzed. The key factors affecting the local fiscal revenue were found out. Also, using traditional time series analysis and multiple regression analysis method, we established a more complete local fiscal revenue forecast model to forecast the fiscal revenue of Guizhou province in 2015-2016.
Keywords:Multiple Regression Analysis, Holt Exponential Smoothing Prediction, Prediction Model

基于大数据技术的政府财政收入预测
—以贵州省为例
罗慢,王群,杨伊玲,梅俊雷
贵州师范学院,贵州 贵阳

收稿日期:2016年11月29日;录用日期:2016年12月12日;发布日期:2016年12月23日

摘 要
本文结合贵州财政收入的构成内容和结构特点,利用R软件,对收集的数据进行整理分析,找出影响地方财政收入的关键影响因素,使用传统时间序列和多元回归分析方法相结合,建立较为完整的地方财政收入预测模型,对贵州省2015~2016年的财政收入进行预测。
关键词 :多元回归分析,Holt指数平滑预测,预测模型

1. 研究目的
构建贵州省历史财政收入数据与同期社会经济发展相关的数据库,梳理影响财政收入关联指标,分析、识别出影响财政收入的关键因素;研究各影响因素与财政收入的相关性,精选出财政收入评价指标,研究并建立贵州省2015~2016年财政收入预测的参考模型。
2. 数据整理
2.1. 数据预处理
数据来源于中国统计年鉴(http://www.nianjianku.com/),初步选取贵州省财政收入相关的指标变量14个,在EXCEL中对选取的指标数据进行整理。样本数据预处理中出现了缺失值,如2004年,2005年,2006年的税收收入的数据是缺失的,如表1所示。
2.1.1. 缺失值处理
在贵州财政收入的数据中出现明显的缺失值现象,出现缺失值的可能原因有:第一、统计局没有录入数据;第二、国家政策有所改动;第三、数据的丢失。因此对于丢失的数据我们用数据挖掘中的一些方法进行处理。在此我们要研究税收收入与相应关联指标的影响,因此我们需要的是缺失指标的一个趋势,且国家的财政收入指标是缓慢变化的,因此第一和第二种缺失值不会出现剧增或者剧减,因此可以采用数据处理方法求出缺失值。常用的求缺失值的方法有平均法、移动平均法、时间序列推测和加权调整。对历年的税收收入做简单的散点图,发现该序列随时间呈线性指数关系,对缺失数据列采用时间序列分析,我们利用了霍尔特(Holt)两参数指数平滑法 [1] 推算缺失值序列,结果如表2。
2.1.2. 数据标准化处理
由于数据存在不同的量纲,采用Z-Score值标准方法对数据进行标准化处理。设数据为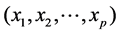 ,其均值为
,其均值为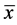 ,标准差为
,标准差为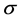 ,标准化公式如下:
,标准化公式如下:
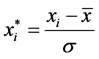
3. 模型的建立与求解
3.1. 回归模型的建立
设响应变量与解释变量之间有线性关系,则多元线性回归模型 [2] 为:
Table 1. Partial missing values of the original data
表1. 原始数据的部分缺失值
注:红色代表缺失值。
Table 2. Predicted value of missing value (100 million yuan)
表2. 缺失值的预测值(亿元)
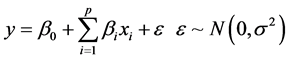 (1)
(1)
其中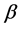 是
是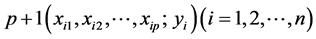 个未知参数,
个未知参数,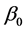 是回归常数,
是回归常数,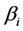 为回归系数,
为回归系数,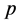 是解释变量的个数,
是解释变量的个数,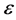 代表随机误差项。设是
代表随机误差项。设是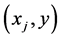 的
的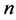 组解释变量的观测数据,线性回归模型用矩阵表示为:
组解释变量的观测数据,线性回归模型用矩阵表示为:
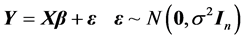 (2)
(2)
(2)式中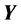 是
是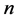 维变量的观测向量(响应变量),
维变量的观测向量(响应变量),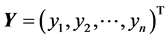 ,
,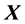 是一个
是一个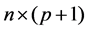 阶设计矩阵,其形式为
阶设计矩阵,其形式为
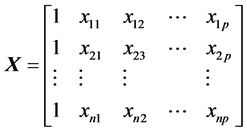
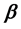 是估计参数向量(回归系数向量),
是估计参数向量(回归系数向量),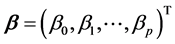 ;
;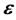 是服从正态分布
是服从正态分布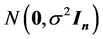 的
的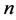 维随机向量,
维随机向量,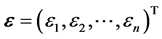 ,由最小二乘法原理求得回归参数
,由最小二乘法原理求得回归参数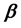 的估计值为
的估计值为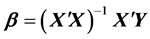 。
。
求得回归方程之后,进一步对回归模型进行检验。
3.2. 回归模型的求解与分析
首先绘制财政总收入与各指标变量之间的散点图,初步剔除对财政总收入影响不显著的变量由图1




Figure 1. Scatter diagram
图1. 散点图
可看出,就业人数和卫生机构数这两个解释变量的分布情况可知,分布点没有规律并且不呈现任何趋势;说明就业人数和卫生机构数对财政总收入影响不显著,所以我们可以初步剔除这两个变量。初步建立回
归模型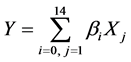 进行回归分析。本文选用Backward法逐步回归进行线性回归,R软件运行结果如图2。
进行回归分析。本文选用Backward法逐步回归进行线性回归,R软件运行结果如图2。
从图2可以看出,逐步回归之后,最终筛选出影响贵州省财政总收入的主要影响因素7个,在此基础之上,建立多元线性回归预测模型对贵州省的财政总收入进行预测。以财政总收入作为响应变量,选取的解释变量如表3所示。
利用以上指标建立多元回归预测模型对财政总收入进行预测,建立的回归预测模型为:
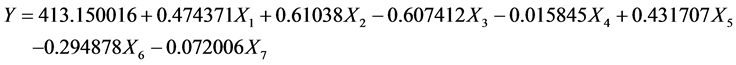
3.3. 回归模型的拟合优度和显著性检验
从图2看出,决定系数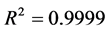 ,调整后的
,调整后的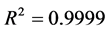 ,检验统计量
,检验统计量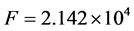 ,
,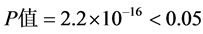 ;由决定系数和
;由决定系数和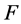 检验来看,回归方程高度显著,说明
检验来看,回归方程高度显著,说明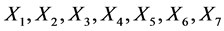 ,整体上对
,整体上对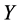 有高度显著的线性影响。从回归系数的显著性检验来看,解释变量
有高度显著的线性影响。从回归系数的显著性检验来看,解释变量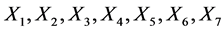 对
对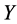 均有显著影响,其中
均有显著影响,其中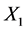 个人储蓄存款的
个人储蓄存款的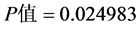 最大,但仍然在5%的显著性水平上对
最大,但仍然在5%的显著性水平上对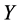 高度显著,这说明在多元线性回归中不能仅凭简单相关系数的大小来决定指标变量的取舍。
高度显著,这说明在多元线性回归中不能仅凭简单相关系数的大小来决定指标变量的取舍。
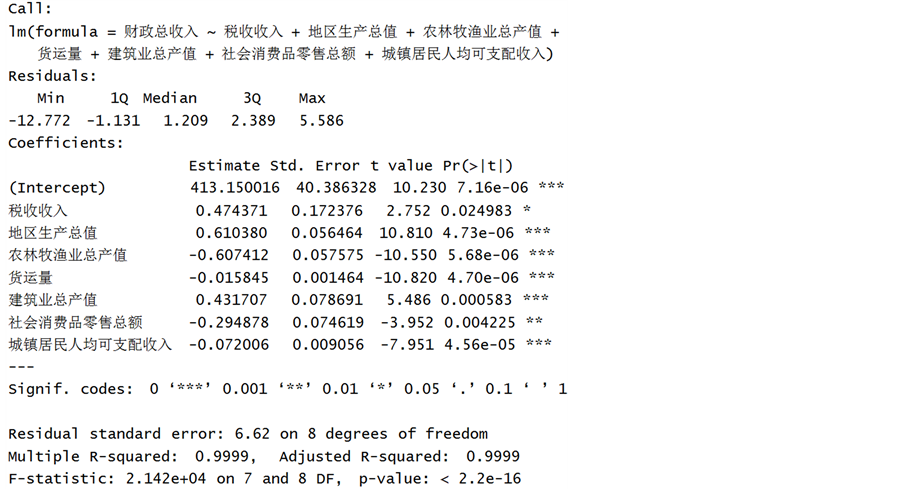
Figure 2. The results of regression analysis
图2. 回归分析结果
Table 3. The main influencing factors of the total fiscal revenue in Guizhou Province
表3. 贵州省财政总收入的主要影响因素
3.4. 模型诊断
由图3中红线的分布可知,各残差值基本在0轴水平线附近随机波动,途中的曲线与残差的0轴水平线没什么差异,也接近于直线,因此,财政总收入与其他变量之间的线性关系假定成立,各指标变量间线性不相关。
图4可以看出,各个点基本上在直线周围随机分布,没有固定模式,因此,在财政总收入与其他变量的线性模型中,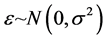 ,关于随机误差项均值为零、同方差的正态性假定基本成立。
,关于随机误差项均值为零、同方差的正态性假定基本成立。
3.5. 结果分析
对各指标变量的预测值建立数据框,利用多元回归预测2015~2016年贵州省财政总收入,在95%的置信水平下,R运行的结果如表4。
从表4中看出,2015年财政总收入在95%的置信水平下预测值为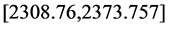 亿元,2016年财政总收入额度为
亿元,2016年财政总收入额度为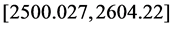 亿元。
亿元。
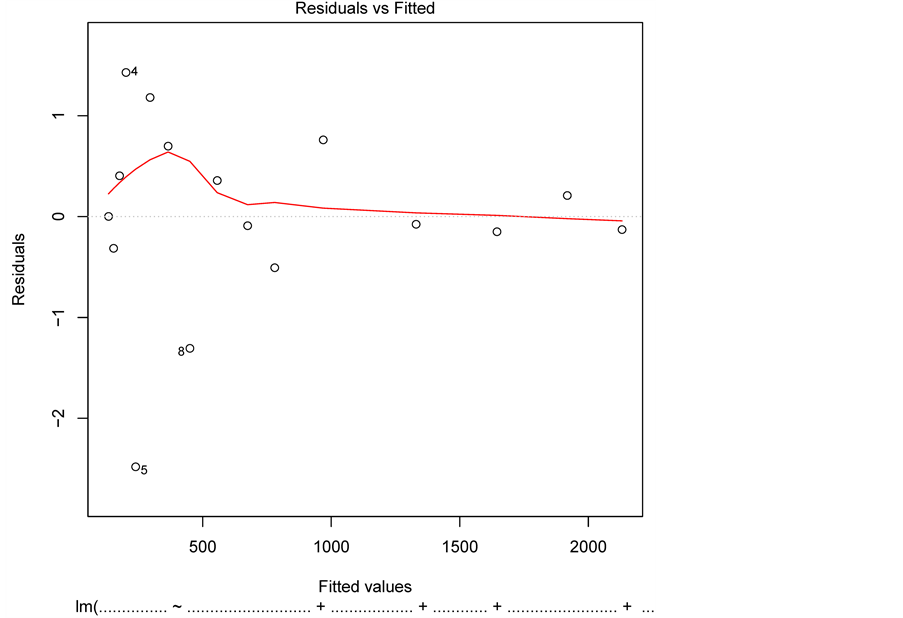
Figure 3. Residual diagnostic chart
图3. 残差诊断图
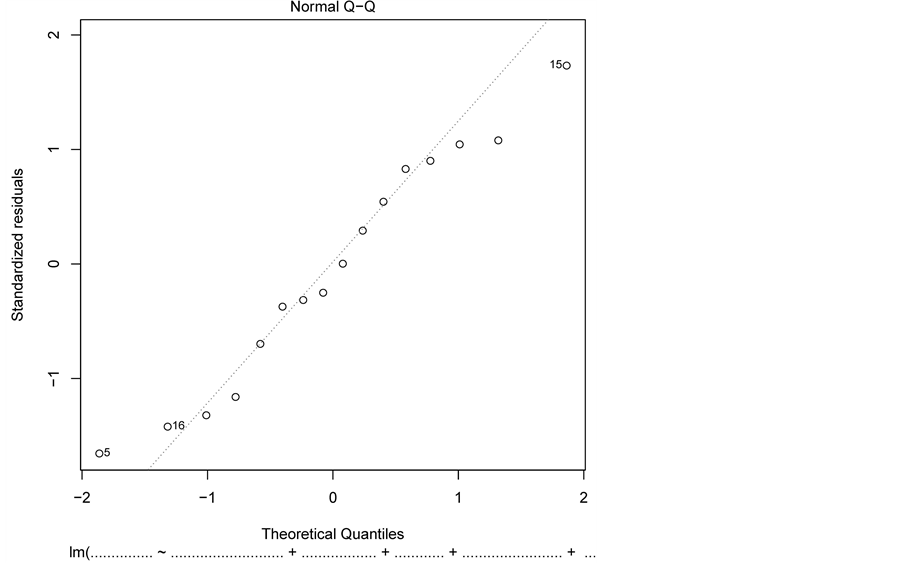
Figure 4. Normal diagnosis
图4. 正态性诊断图
Table 4. Total fiscal revenue of Guizhou Province in 2015-2016 (100 million yuan)
表4. 贵州省2015~2016年财政总收入(亿元)
4. 模型的作用
回归分析研究的主要对象是客观事物变量间的统计关系,它是建立在对客观事物进行大量实验和观察的基础上用来寻找隐藏在那些看上去是不确定的现象中统计规律性的统计方法。基于影响财政收入的因素分析 [3] 作为回归模型的一个重要作用。多元回归模型对影响财政收入变量之间的关系作出了度量,从模型的回归系数可以发现财政收入变量间的结构关系,给出财政预测的一些量化依据。通过建立财政收入的宏观预测模型就可以对未来作出预测。
5. 总结
通过以上对1999年到2014年贵州财政收入相关的经济指标的分析,以定性与定量相结合的方法建立地方财政收入预测模型,预测贵州省2015年到2016年财政收入,为贵州省2015~2016年财政计划提供参考,对其他地方政府建立财政收入预测提供了一定的参考价值。对模型预测方法进行比较,回归模型表现比较稳定,能够弥补ARIMA模型对结构变化不敏感的缺陷,但是,回归模型的限制条件较多,实际运用过程中有一定的难度,达不到理想状态。本文将两种模型结合起来,能降低模型预测的误差,整体表现良好。
致谢
本课程是我与同伴在指导老师梅老师的亲切关心和悉心指导下完成的,老师经常询问我们研究的进度,并为我们解惑,帮助我们开拓思路,指导论文写作结构。在此谨向梅老师致以诚挚的感谢和崇高的敬意。
基金项目
2015年省级大学生创新培育项目(项目编号:201514223035)。
文章引用
罗 慢,王 群,杨伊玲,梅俊雷. 基于大数据技术的政府财政收入预测—以贵州省为例
Government Revenue Forecast Based on Big Data Technology—Taking Guizhou Province as an Example[J]. 统计学与应用, 2016, 05(04): 373-379. http://dx.doi.org/10.12677/SA.2016.54040
参考文献 (References)
- 1. 王燕. 时间序列分析——基于R [M]. 北京: 中国人民出版社, 2015.
- 2. 王国丽, 陈晓飞, 刘刊, 姜国勇. 回归分析在水科学中的应用综述[J]. 中国农村水利水电, 2004(11): 40-44.
- 3. 韩仁月. 我国财政支出规模的影响因素研究[D]: [硕士学位论文]. 济南: 山东大学, 2008.
