Advances in Applied Mathematics
Vol.3 No.02(2014), Article
ID:13570,5
pages
DOI:10.12677/AAM.2014.32015
一类广义Bezout矩阵的研究
Jingpeng Sun1, Huazhang Wu1,2*, Haisheng Li1, Lou Chen11School of Mathematical Sciences, Anhui University, Hefei
2Key Laboratory of Intelligent Computing and Signal Processing, Ministry of Education, Anhui University, Hefei
Email: 1946179973@qq.com, *wuhz@ahu.edu.cn
Copyright © 2014 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received: Mar. 20th, 2014; revised: Apr. 17th, 2014; accepted: Apr. 24th, 2014
ABSTRACT
The bases 
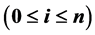 of the polynomial linear space
of the polynomial linear space 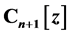 are constructed by the bilinear transformation function. Generalized Bezout matrices under two different bases are investigated. By the generating functions of Bezout matrices, a fast algorithm formula and its corresponding triangular decomposition for the elements of this type of Bezout matrix are given. The formula shows that the cost of the algorithm is
are constructed by the bilinear transformation function. Generalized Bezout matrices under two different bases are investigated. By the generating functions of Bezout matrices, a fast algorithm formula and its corresponding triangular decomposition for the elements of this type of Bezout matrix are given. The formula shows that the cost of the algorithm is![]() . Connection between two Bezout matrices under different bases is discussed. Finally, two numerical examples are given to demonstrate the validity of the theory.
. Connection between two Bezout matrices under different bases is discussed. Finally, two numerical examples are given to demonstrate the validity of the theory.
Keywords:Bilinear Transformation Function, Polynomial Basis, Bezout Matrix, Triangular Decomposition

一类广义Bezout矩阵的研究
孙井鹏1,吴化璋1,2*,李海昇1,陈 楼1
1安徽大学数学科学学院,合肥
2安徽大学教育部智能计算与信号过程重点实验室,合肥
Email: 1946179973@qq.com, *wuhz@ahu.edu.cn
收稿日期:2014年3月20日;修回日期:2014年4月17日;录用日期:2014年4月24日

摘 要
本文通过双线性变换函数构造多项式空间 的两个基
的两个基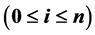
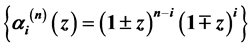 ,分两种情形研究在该多项式基下的一类广义Bezout矩阵。通过Bezout矩阵的生成函数给出该矩阵元素的一个快速计算公式和对应的三角分解公式,该计算公式所需工作量为
,分两种情形研究在该多项式基下的一类广义Bezout矩阵。通过Bezout矩阵的生成函数给出该矩阵元素的一个快速计算公式和对应的三角分解公式,该计算公式所需工作量为![]() 。讨论了两个不同基的广义Bezout矩阵之间的联系。最后,举两个数值例子进行验证。
。讨论了两个不同基的广义Bezout矩阵之间的联系。最后,举两个数值例子进行验证。
关键词
双线性变换函数,多项式基,Bezout矩阵,三角分解

1. 引言
由于Bezout矩阵在多项式求根理论、线性控制系统理论、结构矩阵理论等领域有着广泛的应用(如见文献[1] [2] 等),近年来受到了数学工作者的高度重视。在Bezout矩阵的研究中,将标准幂基下的经典Bezout矩阵推广到一般多项式基下来研究是近年来常见的一个研究方向(如[3] -[6] ),并且关于经典Bezout 矩阵的Barnett分解公式、和伴侣矩阵的缠绕关系以及通过Vandermonde矩阵的对角约化三个方面的性质对一般多项式基下广义Bezout矩阵也成立。关于一般多项式基,通常考虑的是复数域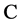 上次数不超过
上次数不超过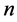 的多项式线性空间
的多项式线性空间 中次数逐渐递增且满足三项递推关系的一个基([5] [6] )。而对于更一般情形的多项式基下的多项式Bezout矩阵,目前多数文献只涉及到它的理论方面的研究,关于它的元素和求逆公式等计算方面的问题鲜有讨论。
中次数逐渐递增且满足三项递推关系的一个基([5] [6] )。而对于更一般情形的多项式基下的多项式Bezout矩阵,目前多数文献只涉及到它的理论方面的研究,关于它的元素和求逆公式等计算方面的问题鲜有讨论。
最近,Bini与Gemignani[7] 研究了在Bernstein基下的Bezout矩阵,讨论了该矩阵的计算公式和位移结构。本文将讨论一类特殊多项式基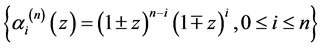 下的广义Bezout矩阵。这类多项式的特殊性表现在
下的广义Bezout矩阵。这类多项式的特殊性表现在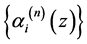 可以作为
可以作为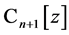 的一个基,基中每个多项式都是
的一个基,基中每个多项式都是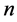 次的,这一点与Bernstein多
次的,这一点与Bernstein多
项式相类似。容易看出,基 中多项式元素来自于双线性变换函数
中多项式元素来自于双线性变换函数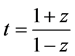 或
或 的分子与分
的分子与分
母。该函数建立了上下复半平面之间的相互转换,这在复分析教材里经常用到。另外,若对任意次数不超过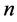 的多项式
的多项式 ,用基
,用基 可表示为
可表示为

则新多项式
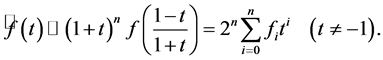
在标准幂基下的系数与 在基
在基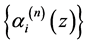 下的系数对应成比例,从而在讨论多项式的结式等相关问题[1] 时带来了方便。众所周知,结式矩阵与多项式的最大公因式和Bezout矩阵之间有着紧密的联系。
下的系数对应成比例,从而在讨论多项式的结式等相关问题[1] 时带来了方便。众所周知,结式矩阵与多项式的最大公因式和Bezout矩阵之间有着紧密的联系。
2. 广义Bezout矩阵元素的计算
给定两个多项式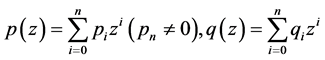 ,由下面二元多项式
,由下面二元多项式

所确定的矩阵![]() 称为由多项式
称为由多项式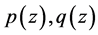 生成的关于标准幂基下的Bezout矩阵[8],记作
生成的关于标准幂基下的Bezout矩阵[8],记作![]() 。显然
。显然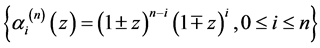 也是
也是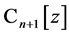 的一个基,但该基中的每一个多项式的次数都是
的一个基,但该基中的每一个多项式的次数都是 次的。对上式进行改写为
次的。对上式进行改写为
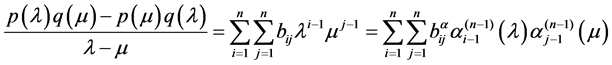 , (1)
, (1)
称矩阵![]() 为由多项式
为由多项式 生成的关于基
生成的关于基 的广义Bezout矩阵,记作
的广义Bezout矩阵,记作![]() 。
。
下面讨论在基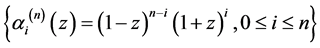 下的广义Bezout矩阵元素
下的广义Bezout矩阵元素![]() 的计算公式,我们有下面的定理。
的计算公式,我们有下面的定理。
定理2.1:取基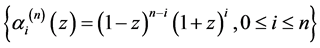 ,并设
,并设
 。
。
那么由(1)所确定的关于基 的广义Bezout矩阵
的广义Bezout矩阵![]() 的元素
的元素![]() 可以通过下列公式计算:
可以通过下列公式计算:
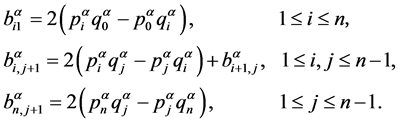 (2)
(2)
该计算方法的工作量为![]() 数量级。
数量级。
证明:首先由定义(1)得
 (3)
(3)
其中上式第一部分为
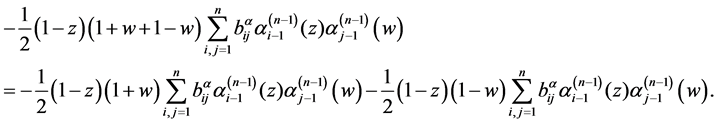
第二部分
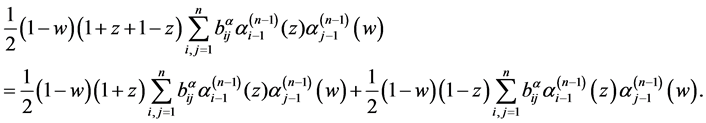
将以上两部分代入(3)得:
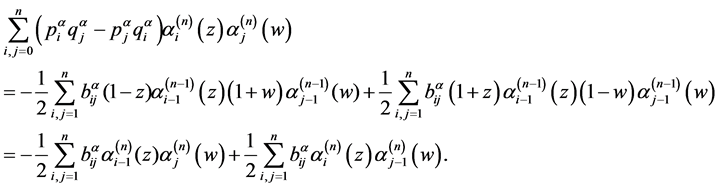
比较![]() (
(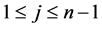 )的系数,有
)的系数,有
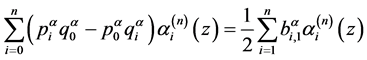 ,
,
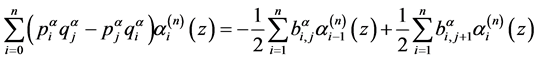 。
。
由于 是基,再比较
是基,再比较![]() 的系数,即得定理中(2)的证明。
的系数,即得定理中(2)的证明。
当基取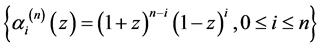 ,类似可证下面的结论。
,类似可证下面的结论。
定理2.2:设线性空间 的基为
的基为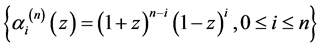 ,多项式
,多项式
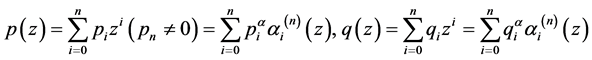
是关于该基的表示式。那么由(1)式所确定的关于基 的广义Bezout矩阵
的广义Bezout矩阵![]() 的元素
的元素![]() 可以通过下列公式计算:
可以通过下列公式计算:
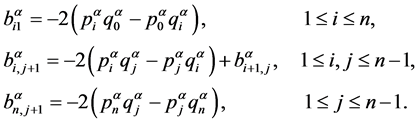 (4)
(4)
该计算公式的计算量为![]() 。
。
如果把定理2.1和2.2中的计算公式写成矩阵乘积的形式,得到下面关于Bezout矩阵的三角分解公式。
推论2.3:设条件如定理2.1,则关于基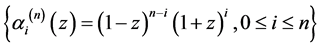 的广义Bezout矩阵的三角分解公式为
的广义Bezout矩阵的三角分解公式为
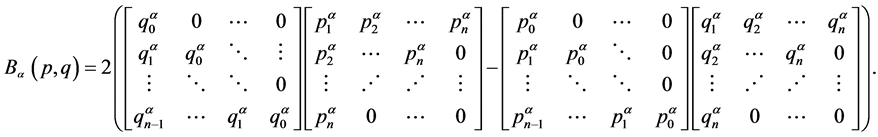
推论2.4:设条件如定理2.2,则关于基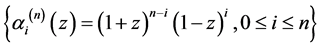 的广义Bezout矩阵的三角分解公式为
的广义Bezout矩阵的三角分解公式为
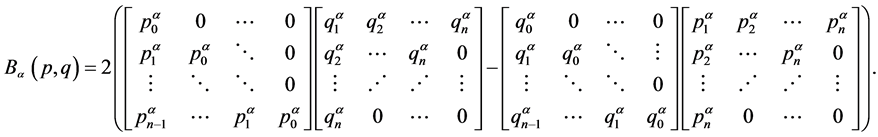
下面我们来考虑一对多项式关于不同基的广义Bezout矩阵之间的联系。为了区别起见,记基分别为
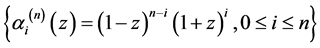 ,
,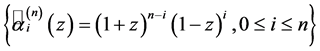 。则基
。则基 的第
的第![]() 项多项
项多项
式为![]() ,此项恰为另一个基
,此项恰为另一个基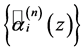 的第
的第 项多项式
项多项式![]() 。因此,就同一对多项式
。因此,就同一对多项式
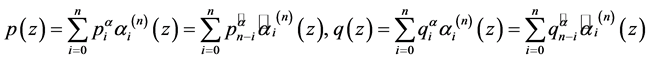
而言,根据(1),由它们生成的广义Bezout矩阵![]() 与
与 的二元函数是相同的,即为
的二元函数是相同的,即为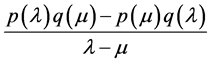 。于是
。于是

由于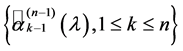 是基,那么Bezout矩阵
是基,那么Bezout矩阵![]() 与
与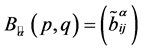 元素之间的联系为
元素之间的联系为
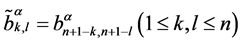 。
。
例2.1:取线性空间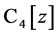 的基为
的基为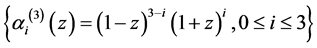 ,令
,令
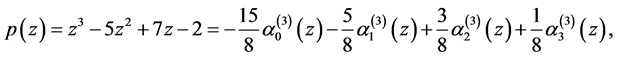
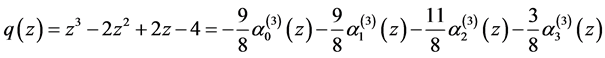 .
.
则按定义(1)计算,由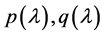 生成的关于基
生成的关于基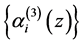 的广义Bezout矩阵是
的广义Bezout矩阵是
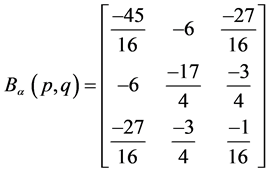 .
.
另一方面,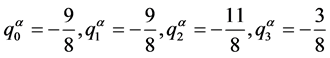
 。按推论2.3的三角分解式为
。按推论2.3的三角分解式为
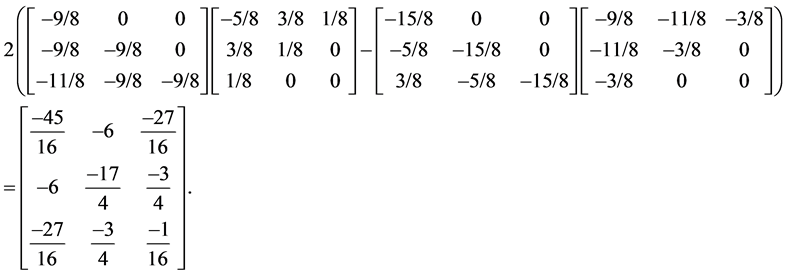
此矩阵与按定义计算所得的广义Bezout 矩阵![]() 完全一致。
完全一致。
例2.2:取线性空间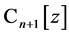 的基为
的基为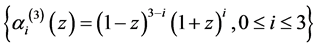 ,多项式
,多项式 如前。关于基
如前。关于基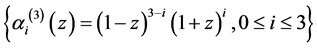 的表达式为
的表达式为
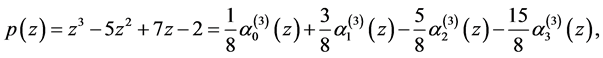
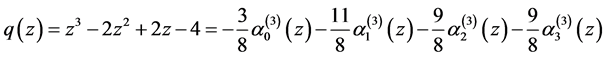 .
.
则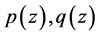 生成的关于基
生成的关于基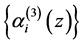 的广义Bezout 矩阵按定义(1)计算是
的广义Bezout 矩阵按定义(1)计算是
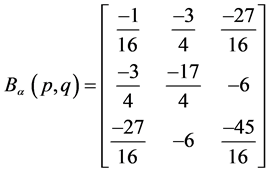 .
.
它与按下面三角分解式计算所得的值完全一致
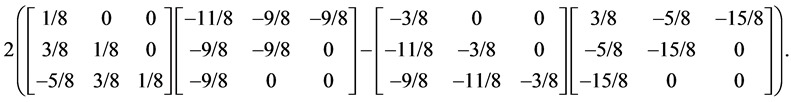
致 谢
感谢审稿人的建议,使得本文更加严谨。
项目基金
安徽省自然科学基金项目(1208085MA02)资助。
参考文献 (References)
- Barnett, S. (1983) Polynomials and linear control system. Marcel Dekker, New York.
- Heinig, G. and Rost, K. (1984) Algebraic methods for toeplitz-like matrices and operators. Operator Theory, 13, Birkhauser, Basel.
- Barnett, S. and Lancaster, P. (1980) Some properties of the Bezoutian for polynomial matrices. Linear and Multilinear Algebra, 9, 99-110.
- Mani, J. and Hartwig, R.E. (1997) Generalized polynomial bases and the Bezoutian. Linear Algebra and Its Applications, 251, 293-320.
- Wu, H.Z. (2010) More on polynomial Bezoutians with respect to a general basis. Electronic Journal of Linear Algebra, 21, 154-171.
- Yang, Z.H. and Hu, Y.J. (2004) A generalized Bezoutian matrix with respect to a polynomial sequence of interpolatory type. IEEE Transactions on Automatic Control, 49, 1783-1789.
- Bini, D.A. and Gemignani, L. (2004) Bernstein-Bezoutian matrices. Theoretical Computer Science, 315, 319-333.

NOTES
*通讯作者。