Advances in Applied Mathematics
Vol.04 No.03(2015), Article ID:15937,8 pages
10.12677/AAM.2015.43034
Numerical Solutions of a Kind of Nonlinear Dynamic Equations of the DNA
Ting Li1, Bo Wang1,2
1School of Mathematics and Statistics, Henan University, Kaifeng Henan
2Institute of Applied Mathematics, Henan University, Kaifeng Henan
Email: wangbo_sdu@163.com
Received: Aug. 5th, 2015; accepted: Aug. 20th, 2015; published: Aug. 24th, 2015
Copyright © 2015 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
We study nonlinear dynamics of DNA double helical under plane based on the rotator model proposed by Yomosa. Through dimensionless disposal, we get the more suitable data for numerical experiments and the relation between the data with the original parameters is also given. We solve a kind of nonlinear Sine-Gordon equations of the model by using the finite difference method, and the results show that the proposed numerical method is effective.
Keywords:DNA, Soliton, The Nonlinear Sine-Gordon Equations, The Dimensionless Disposal, The Finite Difference Method
DNA中一类非线性动力学方程的数值解
李婷1,王波1,2
1河南大学数学与统计学院,河南 开封
2河南大学应用数学研究所,河南 开封
Email: wangbo_sdu@163.com
收稿日期:2015年8月5日;录用日期:2015年8月20日;发布日期:2015年8月24日

摘 要
本文基于Yomosa提出的平面基转子模型数值研究了DNA双螺旋结构的非线性动力学问题。通过对模型参数的无量纲化,得到适于数值实验的数据并给出了与原参数的关系式。利用有限差分方法对模型中的一类非线性Sine-Gordon方程进行数值计算,结果表明本文提出的数值方法是有效的。
关键词 :DNA,孤子,非线性Sine-Gordon方程,无量纲化,有限差分方法

1. 引言
DNA即脱氧核糖核酸是生物遗传信息的负载者和遗传物质。在生命演化和生物体的生长和发育过程中承担着重要角色。近几年来的研究发现DNA动力学问题可以归结为研究非线性Sine-Gordon方程并找出其孤子解的问题。对于这类非线性方程,仅能得到某些特殊条件下的解析解。本文对一类非线性动力学方程无量纲化后进行数值计算,通过数值实验验证了所提出的差分格式对求解此类动力学方程的可行性。
2. 理论模型
1983年日本学者Yomosa提出的平面基转子模型[1] [2] 基本反映了DNA的结构和运动特征,此模型下系统Hamiltonian量可以表示为:
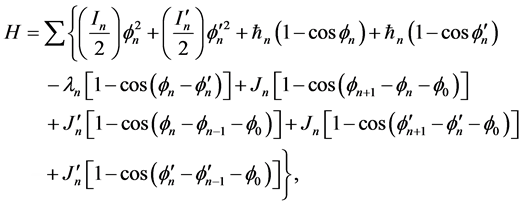 (1)
(1)
其中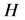 是系统Hamiltonian量,
是系统Hamiltonian量,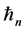 和
和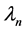 分别表示第
分别表示第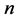 个碱基对的局域场和氢键间的相互作用常数;
个碱基对的局域场和氢键间的相互作用常数; 和
和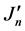 分别表示DNA双螺旋链上第
分别表示DNA双螺旋链上第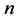 个碱基对有关的相互作用常数;
个碱基对有关的相互作用常数;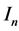 和
和 是第
是第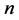 个碱基对的转动惯量;
个碱基对的转动惯量;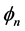 和
和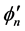 分别表示第
分别表示第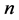 个碱基对在垂直于螺旋轴平面内绕双螺旋链作转动的转角。
个碱基对在垂直于螺旋轴平面内绕双螺旋链作转动的转角。
由欧拉–拉格朗日方程,可得到第 对碱基对的动力学方程为:
对碱基对的动力学方程为:
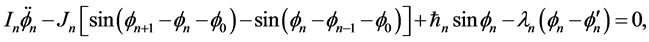 (2)
(2)
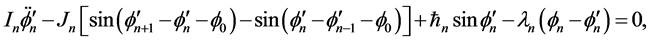 (3)
(3)
实验表明,DNA分子系统的结构畸变和局部涨落是较小的,也就是说碱基的运动,氢键的震动和内部分子的集体激发是较小的,即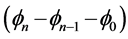 和
和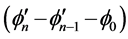 +等项的相对变化足够小,于是可用连续性近似:
+等项的相对变化足够小,于是可用连续性近似:

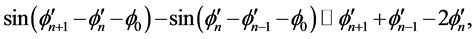

同样由实验可知,可以把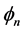 和
和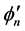 看作是
看作是 的缓变函数作连续近似,引入转动角场量
的缓变函数作连续近似,引入转动角场量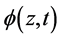 和
和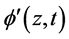 :
:
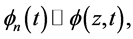
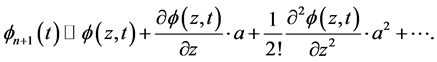
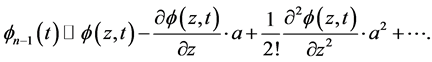
可以得出:
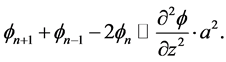
同理可得:

其中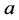 是两个碱基对的距离。
是两个碱基对的距离。
将上述连续近似代入(2)~(3)可得到一组动力学方程组[3] :
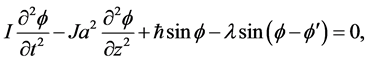 (4)
(4)
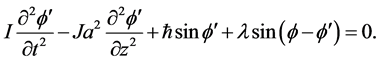 (5)
(5)
3. 非线性Sine-Gordon方程
我们考虑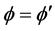 的特殊情况,(4)~(5)化为标准的Sine-Gordon方程:
的特殊情况,(4)~(5)化为标准的Sine-Gordon方程:
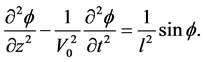 (6)
(6)
其中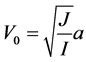 ,
,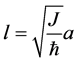 ,其孤子解[3]
[4] 为:
,其孤子解[3]
[4] 为:
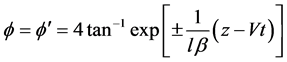 (7)
(7)
其中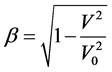 ,
, 是孤子的速度,“±”对应于正反Kink型孤子。
是孤子的速度,“±”对应于正反Kink型孤子。
4. 无量纲化
量纲是物理学中的一个重要概念,在做理论运算和数值计算时,无量纲化处理可以使理论运算简单,数值运算方便模型中出现的参数如表1所示(参数单位选取国际单位制):
对应的矩阵为:
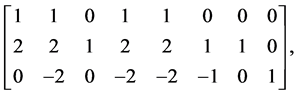

其中I、a、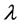 相互独立。根据
相互独立。根据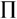 定理[5]
选取I、a、
定理[5]
选取I、a、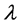 为基本物理量,然后寻找其余变量的量纲。
为基本物理量,然后寻找其余变量的量纲。
以 为例,对应的线性方程组为:
为例,对应的线性方程组为:
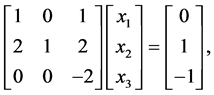

于是,
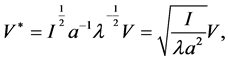
同理,
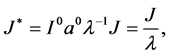
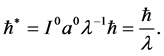
其中上述符号一星表示无量纲化后的参数。
将原模型中参数按照上述各式转换,可得方程(6)无量纲化后的方程为:
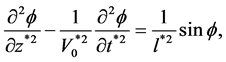 (8)
(8)
其中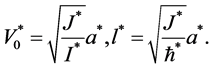
根据文献[6] 的直示踪观察表明,DNA链的复制是从某点开始,以一定的速度向前推进,对于大肠杆菌中的DNA,其推进速度约为800 bp/s,这里一个bp长度为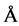
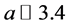 ;由文献[6] [7]
,B-DNA中的平均堆积能为:
;由文献[6] [7]
,B-DNA中的平均堆积能为: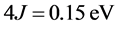 ,氢键的相互作用能为:
,氢键的相互作用能为: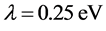 ;由文献[8]
我们取局域能的平均值:
;由文献[8]
我们取局域能的平均值: ;根据文献[9]
中的结果取
;根据文献[9]
中的结果取 。
。
模型中的参数在无量纲化前后的数值对比如表2所示。
表1. 模型中的参数
表2. 模型中参数无量纲化前后的对比表
5. 数值实验
此类非线性Sine-Gordon方程具有2p-Kink解[10] ,即 ,
,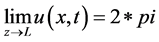 所以在数值计算过程中可选取Dirchlet边界条件。具体考虑如下方程的初边值问题,对非线性Sine-Gordon方程进行有限差分计算[11]
:
所以在数值计算过程中可选取Dirchlet边界条件。具体考虑如下方程的初边值问题,对非线性Sine-Gordon方程进行有限差分计算[11]
:
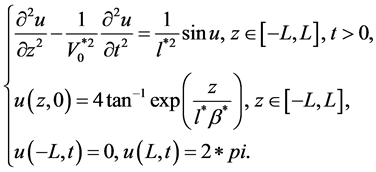 (9)
(9)
其中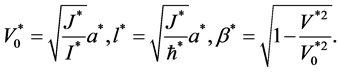
将区域 进行剖分,
进行剖分,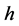 为空间步长,且
为空间步长,且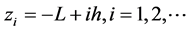 ,
,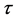 为时间步长,且
为时间步长,且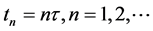 ,本文采用的符号如下:
,本文采用的符号如下:

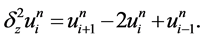
5.1. 差分格式
对于上述Sine-Gordon方程构造如下差分格式:
格式1:
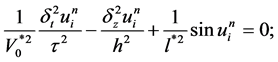
格式2:
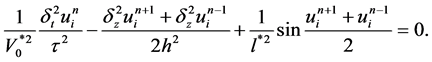
5.2. 局部截断误差
格式1中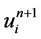 、
、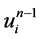 、
、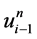 、
、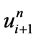 分别在网络节点
分别在网络节点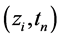 处做Taylor展开,得到:
处做Taylor展开,得到:
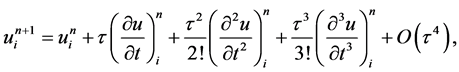
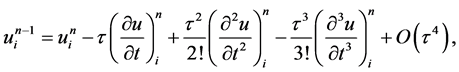
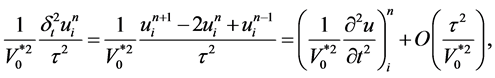

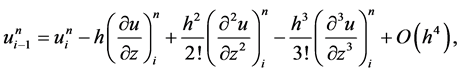
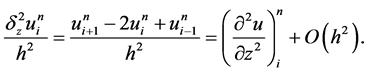
所以此格式关于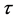 二阶相容,关于
二阶相容,关于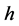 二阶相容,其截断误差为
二阶相容,其截断误差为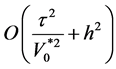 。
。
格式2中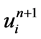 、
、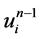 、
、 、
、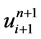 、
、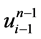 、
、 分别在网络节点
分别在网络节点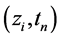 处做Taylor展开,由上一部分分析可知:
处做Taylor展开,由上一部分分析可知:

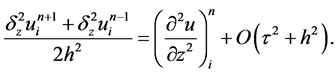
所以此格式关于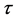 二阶相容,关于
二阶相容,关于 二阶相容,其截断误差为
二阶相容,其截断误差为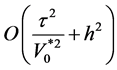 。
。
5.3. 数值计算结果
对(9)在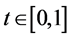 ,
,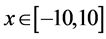 上做数值实验,取时间步长为
上做数值实验,取时间步长为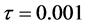 ,空间步长为
,空间步长为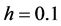 ,我们运用MATLAB语言来完成上述数值实验
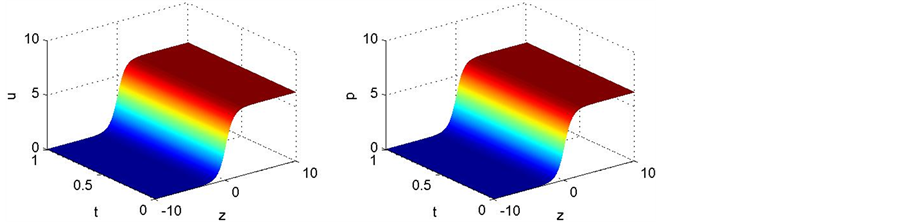
[12] 。图1,图2分别表示差分格式得到的正Kink孤子解的曲面,原方程解析解的曲面,误差绝对值的曲面,差分格式得到的正反Kink孤子解的对比曲线。表3,表4分别给出了在上述条件下原方程的解析解,两种差分格式得到的解,误差的绝对值。
,我们运用MATLAB语言来完成上述数值实验
[12] 。图1,图2分别表示差分格式得到的正Kink孤子解的曲面,原方程解析解的曲面,误差绝对值的曲面,差分格式得到的正反Kink孤子解的对比曲线。表3,表4分别给出了在上述条件下原方程的解析解,两种差分格式得到的解,误差的绝对值。
 (a)
(b)
(a)
(b)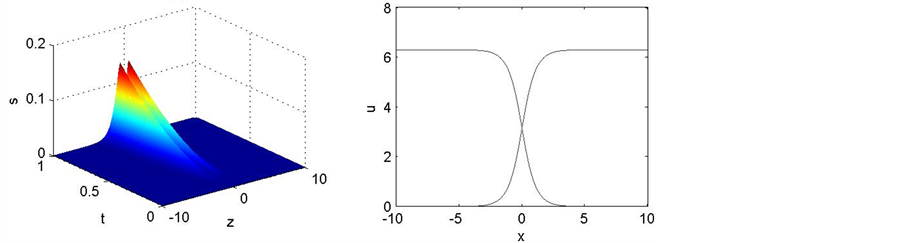 (c)
(d)
(c)
(d)
Figure 1. The numerical solution of the scheme 1 (a), The analytic solution of Sine- Gordon equation (b), The absolute value of error (c), Positive and negative Kink soliton solution contrast of the scheme1 (d)
图1. 格式1得到的数值解的曲面(a),Sine-Gordon方程解析解的曲面(b),误差的绝对值曲面(c),格式1得到的正反Kink孤子解的对比曲线(d)
 (a)
(b)
(a)
(b) (c)
(d)
(c)
(d)
Figure 2. The numerical solution of the scheme 1 (a), The analytic solution of Sine- Gordon equation (b), The absolute value of error (c), Positive and negative Kink soliton solution contrast of the scheme 1 (d)
图2. 格式1得到的数值解的曲面(a),Sine-Gordon方程解析解的曲面(b),误差的绝对值曲面(c),格式1得到的正反Kink孤子解的对比曲线(d)
表3. 格式1数值实验数据
表4. 格式2数值实验数据
本文对模型中的一类非线性动力学方程进行数值计算,首先将模型中的系统Hamiltonian量转换成非线性Sine-Gordon方程,然后对模型中的参数进行无量纲化处理,运用两种差分格式对Sine-Gordon方程进行数值实验,并且对数值实验的结果进行误差分析,进而验证了上述数值方法的有效性。
文章引用
李婷,王波. DNA中一类非线性动力学方程的数值解
Numerical Solutions of a Kind of Nonlinear Dynamic Equations of the DNA[J]. 应用数学进展,
2015, 04(03): 277-284. http://dx.doi.org/10.12677/AAM.2015.43034
参考文献 (References)
- 1. Yomosa, S. (1983) Solition excitations in deoxyribonucleic acid (DNA) double helices. Physical Review A, 27, 2120- 2125. http://dx.doi.org/10.1103/PhysRevA.27.2120
- 2. Yomosa S. (1984) Solition excitations in deoxyribonucleic acid (DNA) double helices. Physical Review A, 30, 474-480. http://dx.doi.org/10.1103/PhysRevA.30.474
- 3. 唐卫东, 庞小峰, 朱德煦 (1996) DNA的震动–内激发–转子模型. 生物数学学报, 1, 65-72.
- 4. 郭柏灵, 庞小峰 (1987) 孤立子. 科学出版社, 北京.
- 5. 刘峰, 贾多杰, 李小礼, 席国柱, 吉永林 (2008) 无量纲化的方法. 安顺学院学报, 3, 78-80.
- 6. Zang, C.T. (1987) Soliton excitations in deoxyribonucleic acid (DNA) double helices. Physical Review A, 15, 885-891.
- 7. Su, W.X. (1984) Scientirum Naturalium Vniv. Intramogolical Sinica, 15, 203-211.
- 8. 庞小峰 (1996) DNA生物大分子的动力学特性与生物功能(II). 黄淮学刊, 2, 23-31.
- 9. 王瞾燚 (2007) DNA动力学特性研究和DNA中孤子传递的计算机模拟. 硕士学位论文, 电子科技大学, 成都.
- 10. 唐卫东, 庞小峰 (1991) DNA动力学特性及其空间组态. 华东师范大学学报, 3, 57-63.
- 11. Thomas, J.W. (1997) Numerical partial differential equations: Finite difference methods. 世界图书出版公司, 北京.
- 12. 彭芳麟 (2004) 数学物理方程的MATLAB解法与可视化. 清华大学出版社, 北京.
