Advances in Applied Mathematics
Vol.04 No.04(2015), Article ID:16421,4
pages
10.12677/AAM.2015.44045
G-Design with Three Groups
Li Zhu, Jian Wang
Nantong Vocational University, Nantong Jiangsu
Received: Nov. 2nd, 2015; accepted: Nov. 19th, 2015; published: Nov. 26th, 2015
Copyright © 2015 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
As a special example of the candelabra systems (CQS), G-design is the extension of group divisible designs (GD), which plays an important role in quadruple systems’ construction. With application of Stern and Lenz’s result on one-factorization of graphs, by direct construction, it is given that the sufficient and necessary condition for the existence of the G-design with three groups  is that
is that .
.
Keywords:t-Designs, Quadruple Systems, Candelabra Systems, G-Design

三个组的G-设计
朱莉,王建
南通职业大学,江苏 南通

收稿日期:2015年11月2日;录用日期:2015年11月19日;发布日期:2015年11月26日

摘 要
G-设计是可分组设计(GD)的推广,同时又是烛台型设计(CQS)的特例,它在四元系设计中起到重要作用。文章应用Stern和Lenz关于图因子分解的结论,通过直接构造法,得到具有三个组的G-设计 存在的充分必要条件:
存在的充分必要条件: 。
。
关键词 :t-设计,四元系,烛台型设计,G-设计

1. 引言
设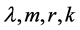 和t是给定的正整数,G-设计(记为
和t是给定的正整数,G-设计(记为 )是一个三元组(X, A, B),其中X是一个
)是一个三元组(X, A, B),其中X是一个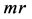 元点集,A构成X的一个划分,B是X的一些子集组成的一个子集族,X的元素叫点,A的元素叫组,B的元素叫区组,满足(1)对任意
元点集,A构成X的一个划分,B是X的一些子集组成的一个子集族,X的元素叫点,A的元素叫组,B的元素叫区组,满足(1)对任意 ,都有
,都有 ;(2)对任意
;(2)对任意 ,都有
,都有 ;(3)对任意
;(3)对任意 与任意
与任意 ,都有
,都有 ;(4)对于X中每个t元子集T与任意
;(4)对于X中每个t元子集T与任意 ,如果
,如果 ,则T恰好包含于B中
,则T恰好包含于B中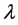 个区组。
个区组。 时,
时,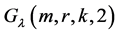 记为
记为 。
。
当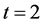 时,G-设计
时,G-设计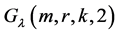 就是大家熟知的可分组设计或GD设计(参见[1] )。当
就是大家熟知的可分组设计或GD设计(参见[1] )。当 时,G-设计
时,G-设计 是柄为0的烛台型四元系
是柄为0的烛台型四元系 ,而烛台型四元系在四元系中起到相当重要的作用(参见[2] )。Mills [3] [4] ,Hartman [5] [6] 研究了
,而烛台型四元系在四元系中起到相当重要的作用(参见[2] )。Mills [3] [4] ,Hartman [5] [6] 研究了 ,得到了一些结论。当
,得到了一些结论。当 时,易知
时,易知 存在的充分必要条件是:
存在的充分必要条件是: (参见[4] )。本文讨论当
(参见[4] )。本文讨论当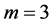 时,
时,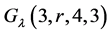 的存在性。我们给出
的存在性。我们给出 存在的充分必要条件是:
存在的充分必要条件是: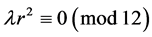 。
。
文中用到的组合设计及图论方面的名词术语均参照著作[1] 和[7] 。
2. 预备知识
定理2.1 存在的必要条件是:
存在的必要条件是: 。
。
证明: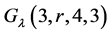 中有
中有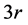 个点,不同的三元点集共有
个点,不同的三元点集共有 个,其中能出现在区组中的有
个,其中能出现在区组中的有 ,而一个区组含有四个三元集,一个三元集可出现在
,而一个区组含有四个三元集,一个三元集可出现在 个区组中,所以,
个区组中,所以, 中的区组数为
中的区组数为 ,因而,
,因而, 。再设
。再设 是设计中给定的点,能和
是设计中给定的点,能和 组成三元集的点对共有
组成三元集的点对共有 个,其中能出现在区组中的有
个,其中能出现在区组中的有 个,且每个三元集可出现在
个,且每个三元集可出现在 个区组中,而一个区组中能和
个区组中,而一个区组中能和 组成三元集的点对有三个,所以,
组成三元集的点对有三个,所以,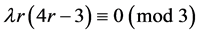 。综上两点,可得
。综上两点,可得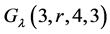 存在的必要条件是
存在的必要条件是 。
。
上述 存在的必要条件可分类等价于以下四种情形
存在的必要条件可分类等价于以下四种情形
1) 且
且 或
或
2) 且
且 或
或
3) 且
且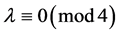 或
或
4) 且
且 。
。
为证 存在的充分性,我们需要图1-因子分解的有关知识。记G是具有个g点的图,其点集为
存在的充分性,我们需要图1-因子分解的有关知识。记G是具有个g点的图,其点集为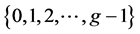 。设
。设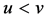 ,图G的边
,图G的边 的差定义为
的差定义为 和
和 中小的一个。我们记图G的边
中小的一个。我们记图G的边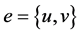 的差为
的差为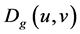 或
或 ,也即是
,也即是
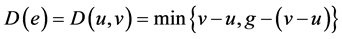 。
。
对于任何一个子集 (
(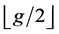 表示不大于
表示不大于 的最大整数),我们定义
的最大整数),我们定义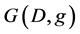 是一个图,其点集为
是一个图,其点集为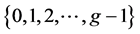 ,边集为
,边集为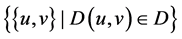 ,即包含所有差属于
,即包含所有差属于 的边。
的边。
图 的一个子图
的一个子图 如果包含了
如果包含了 的全部点,则
的全部点,则 为
为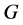 的生成子图。如果图
的生成子图。如果图 的一个生成子图
的一个生成子图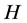 是1-正则的,则称
是1-正则的,则称 是
是 的1-因子。如果图
的1-因子。如果图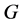 的边集可表示为它的某些1-因子的并,则称
的边集可表示为它的某些1-因子的并,则称 存在的1-因子分解,或称
存在的1-因子分解,或称 可1-因子化。下面的引理来自Stern和Lenz [8] ,我们在第3节的证明中将会用到,其中
可1-因子化。下面的引理来自Stern和Lenz [8] ,我们在第3节的证明中将会用到,其中 表示
表示 和
和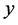 的最大公约数。
的最大公约数。
引理2.2 (Stern和Lenz)如果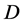 包含一个元素
包含一个元素 使得
使得 是偶数,则图
是偶数,则图 存在1-因子分解。
存在1-因子分解。
3. 主要结论
引理3.1如果 存在,则对于任意正整数
存在,则对于任意正整数 ,
, 存在。
存在。
证明:将 的每个区组重复s倍,即得
的每个区组重复s倍,即得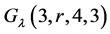 。
。
由引理2.1结合引理3.1,为证主要结论,我们只需考虑以下四种情形
1) 且
且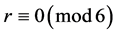 ;
;
2) 且
且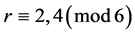 ;
;
3) 且
且 ;
;
4)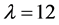 且
且 。
。
引理3.2当 时,
时, 存在。
存在。
证明:设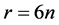 ,记所需设计的点集
,记所需设计的点集 ,组A:{
,组A:{ :
: }
} 。
。
区组B:{ ,
, ,
, ,
, }
}
(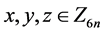 ,
,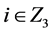 ,
,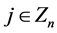 ,
,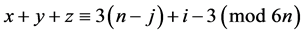 );
);
{ ,
, ,
,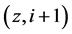 ,
,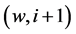 }
}
(由引理2.2,图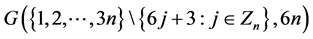 存在1-因子分解,记
存在1-因子分解,记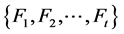 是
是 的1-因子分解,
的1-因子分解,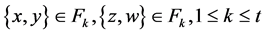 ,
,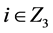 )。
)。
引理3.3当 时,
时, 存在。
存在。
证明:设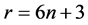 ,记所需设计的点集
,记所需设计的点集 ,组A:{
,组A:{ :
: }
}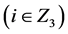 。
。
区组B:{ ,
, ,
, ,
, }
}
( ,
, ,
, ,
, )重复4次;
)重复4次;
{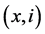 ,
, ,
,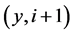 ,
, }
}
( ,
,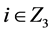 ,
,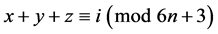 )重复2次;
)重复2次;
{ ,
,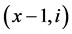 ,
,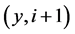 ,
, }
}
( ,
,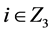 ,
, )重复2次;
)重复2次;
{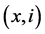 ,
,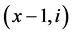 ,
, ,
, }
}
( ,
,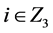 ,
,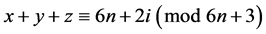 )重复2次;
)重复2次;
{ ,
, ,
,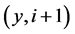 ,
,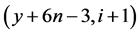 }(
}(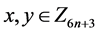 ,
, );
);
{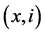 ,
, ,
, ,
, }(
}(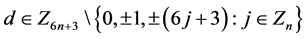 ,
, ,
,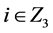 )。
)。
引理3.4当 时,
时,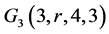 存在。
存在。
证明:设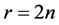 ,记所需设计的点集
,记所需设计的点集 ,组A:{
,组A:{ :
: }
} 。
。
区组B:{ ,
, ,
, ,
,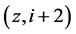 } (
} ( ,
, ,
,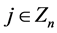 ,
, );
);
{ ,
,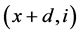 ,
, ,
,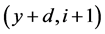 } (
} (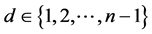 ,
,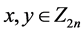 ,
,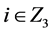 );
);
{ ,
, ,
, ,
, } (
} (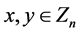 ,
, )。
)。
引理3.5当 时,
时,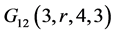 存在。
存在。
证明:设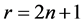 ,记所需设计的点集
,记所需设计的点集 ,组A:{
,组A:{ :
: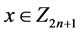 }
} 。
。
区组B:{ ,
, ,
, ,
, }
}
( ,
, ,
, ,
, )重复4次;
)重复4次;
{ ,
,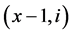 ,
, ,
,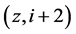 }
}
(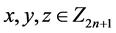 ,
,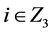 ,
, ,
,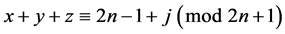 )重复2次;
)重复2次;
{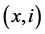 ,
, ,
, ,
, }
}
( ,
, ,
, )重复2次;
)重复2次;
{ ,
,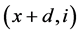 ,
, ,
, }(
}(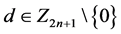 ,
,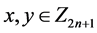 ,
, );
);
{ ,
, ,
, ,
, }(
}( ,
, ,
, )
)
{ ,
, ,
, ,
, }(
}(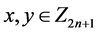 ,
,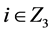 )
)
定理3.6当 时,
时, 存在。
存在。
证明:由引理3.2~3.5,结合引理3.1,可得 存在的充分条件。
存在的充分条件。
结合引理2.1和定理3.6,我们得到本文的主要结论。
定理3.7 存在的充分必要条件是
存在的充分必要条件是 。
。
基金项目
国家自然科学基金项目(11171248和11371207)。
文章引用
朱莉,王建. 三个组的G-设计
G-Design with Three Groups[J]. 应用数学进展, 2015, 04(04): 365-368. http://dx.doi.org/10.12677/AAM.2015.44045
参考文献 (References)
- 1. 沈灏. 组合设计理论[M]. 上海: 上海交通大学出版社, 2008.
- 2. Mohacsy, H. and Ray-Chaudhuri, D.K. (2002) Candelabra Systems and Designs. Journal of Statistical Planning and Inference, 106, 419-448. http://dx.doi.org/10.1016/S0378-3758(02)00226-4
- 3. Mills, W.H. (1981) A Covering of Triples by Quadruples. Congr. Numer, 33, 253-260.
- 4. Mills, W.H. (1990) On the Existence of H Designs. Congr. Numer, 79, 129-141.
- 5. Hartman, A. (1980) Tripling Quadruple Systems. Ars Combinatoria, 10, 255-309.
- 6. Hartman, A. (1994) The Fundamental Construction for 3-Designs. Discrete Mathematics, 124, 107-132.http://dx.doi.org/10.1016/0012-365X(92)00055-V
- 7. Bondy, J.A. and Murty, U.S.R. (1976) Graph Theory with Applications. Macmillan Press, London.
- 8. Stern, G. and Lenz, H. (1980) Sterner Triple Systems with Given Sub-spaces: Another Proof of the Doyen-Wilson Theorem. Bollettino Unione Matematica Italiana (Ser. A), 17, 109-114.