Advances in Applied Mathematics
Vol.06 No.07(2017), Article ID:22545,10
pages
10.12677/AAM.2017.67104
Solution and Establishing of a Selection of Optimal Route for Logistics Vehicles Models under the Uncertain Environment
Ruonan Shen, Youhui Su*
College of Mathematics and Physics, Xuzhou Institute of Technology, Xuzhou Jiangsu
Received: Oct. 9th, 2017; accepted: Oct. 23rd, 2017; published: Oct. 31st, 2017

ABSTRACT
This paper has established the optimal path model under uncertain factors as the subject of research, i.e., from Culture Palace Business Department of Xuzhou Yuantong Express to Nanhu Campus of China University of Mining and Technology. By using the additive property of the normal distribution, the expression of the normal distribution for travel time of each path has been obtained, which is standardized to derive the expression of travel time. When the probability of reaching the end point is determined, the optimal path is the path with the shortest travel time. On this basis, the optimal path algorithm based on depth-first search is designed, and seven different paths are obtained by MATLAB programming. The minimum travel time and the optimal path are obtained.
Keywords:Optimal Path, Normal Distribution Additive, Convolution Formula, Depth-First Search Algorithm
不确定因素下一类物流车最优路径模型 的建立与求解
沈若男,苏有慧*
徐州工程学院 数学与物理科学学院,江苏 徐州

收稿日期:2017年10月9日;录用日期:2017年10月23日;发布日期:2017年10月31日

摘 要
本文以徐州市圆通快递文化宫营业部到中国矿业大学南湖校区为研究对象,建立了不确定因素下最优路径模型,利用正态分布的可加性,得出各条路径的总行驶时间正态分布表达式,并进行标准化,解出行驶时间的表达式。当到达终点的概率确定时,最优路径为行驶时间最少的路径。在此基础上设计了基于深度优先搜索的最优路径算法,运用MATLAB编程,得出7条不同的路径,求出最短行驶时间和最优路径。
关键词 :最优路径模型,正态分布可加性,卷积公式,深度优先搜索算法

Copyright © 2017 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
现在我国社会的物流需求发展很快,城市交通运输状况日益紧张、交通拥堵、交通事故、天气恶劣等许多不确定因素严重影响着物流车的运输,为物流车配送货物找到一条快速可靠的运输路线是物流公司和广大民众的迫切的需求。因此在复杂的交通环境下,分析各种不确定因素,求得最优的物流配送路径,可以为物流车运输找到一条快速可靠的行驶路径,减少物流配送时间、降低物流公司运输的成本,促进物流运输业的发展 [1] [2] [3] 。
不确定因素下最优路径规划和设计问题是一个复杂而神奇的问题,涉及到模糊数学、最优化控制和系统、概率统计、微分方程理论及优化算法等相关知识,从而吸引了许多学者研究不确定因素下最优路径问题 [1] - [8] 。其中:张梦颖 [1] 研究了不确定旅行商路径优化问题,建立了具有相同的需求概率下,期望理论最大的非线性规划模型,并设计了遗传算法,得出了旅行商的车辆最优路径;王君 [2] 对不确定车辆路径问题,建立了基于模糊时间窗的多目标规划模型,并设计了混合搜索策略的启发式算法,得出了令客户满意的最优路径。本论文在这些研究成果 [1] - [6] 的启发下,建立了交通畅通时的不确定因素下的最优路径模型,以同一概率下最短总行驶时间为目标函数,设计了深度优先搜索算法,求出了最优路径。与文献 [1] [2] [3] [4] [5] 相比,本文在不确定因素下利用卷积公式进行了最优路径单目标规划,建立了从起点到终点行驶过程中的不确定性因素下最优行驶路径。
2. 不确定性条件下的最优路径
2.1. 模型假设
1) 假设行驶时间是在满足通达率的情况下、一定范围的随机变量;
2) 假设在交通网络节点上的时间不存在;
3) 各个路段的行驶时间变量相互独立;
4) 假设各个车道之间的行驶状况的影响不存在。
2.2. 模型的准备
根据从徐州市圆通快递文化宫营业部到中国矿业大学南湖校区的交通图(见附录1),当所有路段交通畅通时,在每个路段进行实地调查20次,统计每个路段的行驶时间,对每个路段的行驶时间进行正态性检验,运用SPSS软件得到表1的结果。
由上表可知,各个路段的行驶时间分布的 ,因此接受假设,且各个路段的行驶时间的显著性均大于0.05,因此各路段的行驶时间服从正态分布。路段3行驶时间正态分布拟合图如图1,其中,路段3行驶时间均值为0.92,标准差为0.309。
2.3. 不确定因素下最优路径模型的建立
根据上述正态性检验可知,各个路段上的车辆行驶时间近似服从正态分布,因此设路段k的行驶时间为 ,行驶时间 均值表达式为 ,方差表达式为 ,密度函数表达式为:
下面利用正态分布的可加性,把每条路径上的各个路段进行整合,然后利用卷积公式,给出每条路径的总行驶时间的正态分布密度函数,变形得出最优路径模型。当到达终点的概率一定时,对不同的行驶时间 进行比较,行驶时间最小的路径即为最短路径。
设第1、2个路段的行驶时间分别为 、 ,且 与 相互独立,则有:
则n个路段的总行驶时间 为:
Table 1. Normality test—chi-square test
表1. 正态性检验——卡方检验
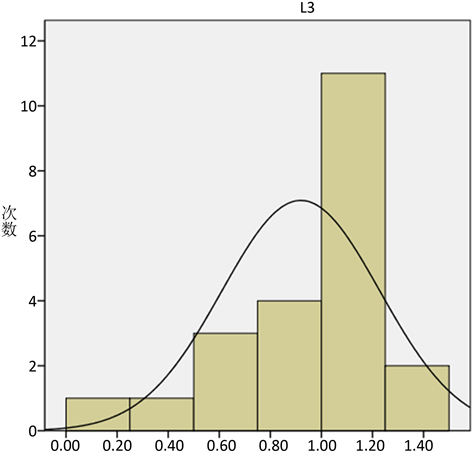
Figure 1. When the traffic is smooth, the travel time distribution curve of the road D3
图1. 交通畅通时,路段D3行驶时间分布拟合曲线
且总行驶时间 也服从正态分布,表达式为:
其密度函数为:
根据正态分布可加性和卷积公式可以得出某条路径的总行驶时间
其中k为路径 的路段数。下面对总行驶时间 这一随机变量进行标准化处理,使其服从标准正态分布,即:
假设从起点到达终点的概率为p,因此可以由以下公式:
解出:
比较 的值,则 所对应的路径即为不确定因素下的最优路径。
综上所述,不确定因素下的最优路径模型的目标函数为:
3. 基于深度优先搜索算法的最优路径求解
本文利用第二章建立的最优路径的可靠性模型,设计深度优先搜索的最优路径算法,求出一般情况下的最优路径。
3.1. 基于深度优先搜索的最优路径算法
3.1.1. 深度优先搜索算法思想 [9] [10]
深度优先搜索(dfs)遍历与树的先序遍历类似。假设给定的图G的初态是:图中所有顶点均未被访问过,我们在G中任选一个顶点i作为深度优先遍历的初始点(起点),则深度优先搜索递归调用包含以下操作:
1) 访问搜索到的顶点 ;
2) 将 顶点的visited数组中的元素值置为1;
3) 搜索 点所有未被访问的邻接点,若该邻接点存在,则从此邻接点开始递归,即开始相同的访问和搜索;若不存在,则返回到上一顶点。
3.1.2. 最优路径算法的理论综述
设从起点(圆通快递文化宫营业部)到终点(中国矿业大学南湖校区),交通网络图中总共有n个交通点,最优路径的搜索步骤如下:
Step1:
根据交通网络的每一个交通点,构建交通网络图的邻接矩阵 、 ,其中a、B每一个索引分别表示网络图上每一条边的时间均值μ和方差σ。
Step2:
给定起始点和终点,深度优先搜索起点到终点的一条连通路径,并将搜索到路径上的交通点名称保存在nextNodes数组中。若目标节点destination与下一个节点中的数相等时,输出路径,所有可能的路径保存在possiablePaths数组中。nextNodes数组中的交通点名称通过一个关联数组Graph寻找到邻接矩阵a、B的索引,从而使用均值μ和方差σ。
Step3:
根据均值μ和方差σ,以及所有可能的路径,计算每条路径的总均值和总方差,分别存放在数组TotalMean和TotalVar中。
Step4:
根据不确定因素下的最优路径模型,由卷积公式可以得到某条路径的总行驶时间 服从正态分布,即:
根据给定的从起点到达终点的概率p,和已存总均值和总方差,计算出某条连通路径的总行驶时间 。
Step5:
比较每条路径 的值,则最优路径即为 所对应的路径。
3.2. 算法的实际应用
根据从徐州市圆通快递文化宫营业部到中国矿业大学南湖校区的具体交通网络图(见附录1),画出如下图2所示的交通简化图。
根据图2和附录1中的交通网络图可以得到:从徐州市圆通快递文化宫营业部到中国矿业大学南湖校区不同的行驶路径总共有7条,具体的行驶路径见下表2。
3.3. 最优路径算法的求解
根据交通网络图以及深度优先搜索算法,编写MATLAB程序,具体程序见附录5程序1。运行程序,得到从起点P到终点Q的这7条路径在概率 下的行驶时间。因此对7条路径进行数据汇总,可以得到各条路径的总均值、总方差、标准差以及当概率 下的分位数,具体数值见下表3。
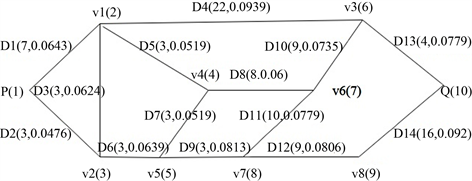
Figure 2. Traffic Simplified Chart
图2. 交通简化图
Table 2. 7 different paths
表2. 7条不同的路径
Table 3. Summary of Data
表3. 数据汇总表
由上表可知:在到达终点的概率p为0.975时, 下的分位数即最短的总行驶时间为31.1975,对应的路径是 。因此最优路径是 ,即为:
4. 结论
本文在研究不确定因素下的最优路径时,将不确定条件进行量化,对行驶时间数据进行正态性检验,根据正态分布建立模型,在到达终点中国矿业大学的概率一定的情况下,行驶时间最短的路径为最优路径。表达式中均值和方差对行驶时间产生影响,在概率一定的情况下,均值和方差越大,路径的行驶时间越大,因此,我们选择行驶时间均值较小且方差小的路径为最优路径。
基金项目
国家自然科学基金资助项目(11501560);江苏省自然科学基金资助项目(BK20151160);江苏省六大人才高峰项目(2013-JY-003);江苏省333高层次人才项目(BRA2016275)。
文章引用
沈若男,苏有慧. 不确定因素下一类物流车最优路径模型的建立与求解
Solution and Establishing of a Selection of Optimal Route for Logistics Vehicles Models under the Uncertain Environment[J]. 应用数学进展, 2017, 06(07): 861-870. http://dx.doi.org/10.12677/AAM.2017.67104
参考文献 (References)
- 1. 张梦颖. 不确定因素下路径规划问题研究[D]: [博士学位论文]. 合肥: 中国科学技术大学, 2016: 21-31.
- 2. 王君. 不确定因素下车辆路径问题建模及优化方法研究[D]: [博士学位论文]. 天津: 天津大学, 2013: 2-8.
- 3. 于福才. 物流企业配送中心选址研究——以绥化申通快递为例[J]. 企业导报, 2014(24): 20-21.
- 4. 雷超. 不确定条件下的移动设施规划与调度优化研究[D]: [博士学位论文]. 北京: 清华大学, 2015: 1-10.
- 5. 廖伟. 考虑共同配送和能耗的车辆路径问题优化研究[D]: [博士学位论文]. 成都: 西南交通大学, 2014: 2-8.
- 6. 刘佳倩, 朱家明. 不确定条件下交通网络的动态最优路径求解算法[J]. 上海工程技术大学学报, 2016, 30(3): 246-251.
- 7. 陆海良, 郁钢, 单宇翔. 基于改进遗传算法的车辆路径优化算法[J]. 工业控制计算机, 2015, 28(10): 74-75.
- 8. 许克平, 曾明月. 彭圆红基于不确定因素下的Floyd算法改进[J]. 中国科技信息, 2016(18): 49-50.
- 9. 杨阳. 基于深度优先搜索的混成系统有界可达性分析[D]: [硕士学位论文]. 南京: 南京大学, 2013: 4-14.
- 10. 唐青松. 深度优先算法在创建树形结构中的应用研究[J]. 计算机技术与发展, 2014(9): 226-229.
附录
附录1
从徐州市圆通快递文化宫营业部到中国矿业大学南湖校区的交通图如下图所示:
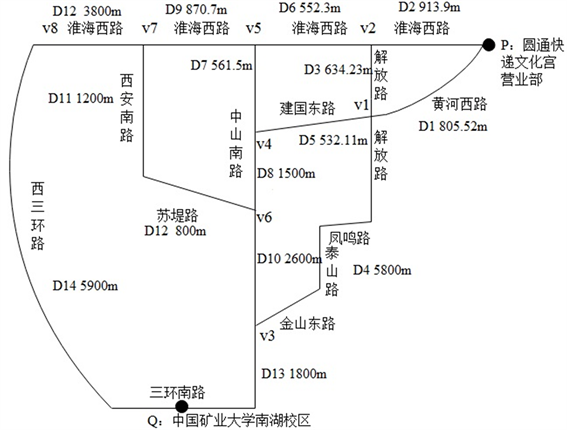
Figure 1. Traffic Simplified Chart
附图1. 交通简化图
附录2
程序1:
基于深度优先搜索的最优路径算法程序如下:
function possiablePaths = findPath(Graph, partialPath, destination, partialWeight)
% findPath按深度优先搜索所有可能的从partialPath出发到destination的路径,这些路径中不包含环路
% Graph: 路网图,非无穷或0表示两节点之间直接连通,矩阵值就为路网权值
% partialPath: 出发的路径,如果partialPath就一个数,表示这个就是起始点
% destination: 目标节点
% partialWeight: partialPath的权值,当partialPath为一个数时,partialWeight为0
pathLength = length(partialPath);
lastNode = partialPath(pathLength); %得到最后一个节点
nextNodes = find(0
GLength = length(Graph);
possiablePaths = [];
if lastNode == destination
% 如果lastNode与目标节点相等,则说明partialPath就是从其出发到目标节点的路径,结果只有这一个,直接返回
possiablePaths = partialPath;
possiablePaths(GLength + 1) = partialWeight;
return;
elseif length( find( partialPath == destination ) ) ~= 0
return;
end
%nextNodes中的数一定大于0,所以为了让nextNodes(i)去掉,先将其赋值为0A=zeros(10,10);
for i=1:length(nextNodes)
if destination == nextNodes(i)
%输出路径
tmpPath = cat(2, partialPath, destination); %串接成一条完整的路径
tmpPath(GLength + 1) = partialWeight + Graph(lastNode, destination); %延长数组长度至GLength+1, 最后一个元素用于存放该路径的总路阻
possiablePaths( length(possiablePaths) + 1 , : ) = tmpPath;
nextNodes(i) = 0;
elseif length( find( partialPath == nextNodes(i) ) ) ~= 0
nextNodes(i) = 0;
end
end
nextNodes = nextNodes(nextNodes ~= 0); %将nextNodes中为0的值去掉,因为下一个节点可能已经遍历过或者它就是目标节点
for i=1:length(nextNodes)
tmpPath = cat(2, partialPath, nextNodes(i));
tmpPsbPaths = findPath(Graph, tmpPath, destination, partialWeight + Graph(lastNode, nextNodes(i)));
possiablePaths = cat(1, possiablePaths, tmpPsbPaths);
end
程序2:
道路畅通(无相关性)时,在到达终点的概率为0.975的条件下,行驶时间求解程序如下:
clear all;
close all;
clc;
%输入均值
A=inf(10,10);
A(1,2)=7;A(2,1)=7;A(1,3)=3;A(3,1)=3;A(2,3)=3;A(3,2)=3;A(2,4)=3;A(4,2)=3;A(2,6)=22;
A(6,2)=22;A(3,5)=3;A(5,3)=3;A(4,5)=3;A(5,4)=3;A(4,7)=8;A(7,4)=8;A(5,8)=3;A(8,5)=3;
A(6,7)=9;A(7,6)=9;A(6,10)=4;A(10,6)=4;A(7,8)=10;A(8,7)=10;A(8,9)=9;A(9,8)=9;A(10,9)=16;
A(9,10)=16;
for i=1:10
A(i,i)=0;
end
TotalMean=findPath(A, 1, 10, 0)%每条路径总均值
%输入方差
B=inf(10,10);
B(1,2)=0.0643;B(2,1)=0.0643;B(1,3)=0.0476;B(3,1)=0.0476;B(2,3)=0.0624;B(3,2)=0.0624;
B(2,4)=0.0519;B(4,2)=0.0519;B(2,6)=0.0939;B(6,2)=0.0939;B(3,5)=0.0639;B(5,3)=0.0639;
B(4,5)=0.0519;B(5,4)=0.0519;B(4,7)=0.06;B(7,4)=0.06;B(5,8)=0.0813;B(8,5)=0.0813;
B(6,7)=0.0735;B(7,6)=0.0735;B(6,10)=0.0779;B(10,6)=0.0779;B(7,8)=0.0779;B(8,7)=0.0779;
B(8,9)=0.0806;B(9,8)=0.0806;B(10,9)=0.092;B(9,10)=0.092;
for i=1:10
B(i,i)=0;
end
TotalVar=findPath(B, 1, 10, 0)%每条路径总方差
%计算行驶时间
T=TotalMean(:,11)+1.96*sqrt(TotalVar(:,11));
知网检索的两种方式:
1. 打开知网页面http://kns.cnki.net/kns/brief/result.aspx?dbPrefix=WWJD
下拉列表框选择:[ISSN],输入期刊ISSN:2324-7991,即可查询
2. 打开知网首页http://cnki.net/
左侧“国际文献总库”进入,输入文章标题,即可查询
投稿请点击:http://www.hanspub.org/Submission.aspx
期刊邮箱:aam@hanspub.org
