以对轮图为缩影图式流形的同胚类数 The Homeomorphic Class number of Graphlike Manifold with Contraction Round Diagrams

doi:10.12677/PM.2012.23018

设为首页加入收藏期刊导航网站地图

期刊菜单

文章导航

Pure Mathematics 理论数学, 2012, 2, 111-116

http://dx.doi.org/10.12677/pm.2012.23018 Published Online July 2012 (http://www.hanspub.org/journal/pm)

The Homeomorphic Class Number of Graphlike

Manifold with Contraction Round Diagrams*

Lin Ping, Shengmin Chen, Youhua Qian #

College of Mathematics, Physics and Information Engineering, Zhejiang Normal University, Jinhua

Email: #zjjhqyh@yahoo.com

Received: Jun. 4th, 2012; revised: Jun. 21st, 2012; accepted: Jul. 1st, 2012

Abstract: This article obtains the number of homeomorphic class of n



by means of classification for

some natural numbers n. It uses Matlab to compute the adjoint matrix of n



and calculate the number of

characteristic polyno mial, and then get the lower bound of the number of homeo morphic class of . For all

natural numbers, it puts forward a method to calculate the upper bound of the number of homeomorphic class

by using Burnside’s lemma.

W

Keywords: Graphlike Manifold; CW Complex; Attaching Map; Round Diagram; Burnside’s Lemma

以对轮图为缩影图式流形的同胚类数*

平麟，陈胜敏，钱有华#

浙江师范大学数理与信息工程学院，金华

Email: #zjjhqyh@yahoo.com

收稿日期：2012 年6月4日；修回日期：2012 年6月21 日；录用日期：2012 年7月1日

摘要：对于某些自然数 n，通过分类法可以得出以对轮图为缩影的所有图式流形的同胚类的类

数，并且用 Matlab 软件算出中每个图式流形的伴随矩阵的不同特征多项式个数，得出同胚类数

的下界。对于所有的自然数 n，利用 Burnside 引理给出了求

W

Wn

W



的同胚类数的上界的一个方法。

关键词：图式流形；CW 复形；粘附映射；对轮图；Burnside引理

1. 引言

自从刘亚星和李起升提出图式流形的概念[1]后，由于对所有的图式流形没有办法进行同胚分类，所以只能

对特殊的几类图式流形进行同胚分类。对以 1n



维单形的一维骨架为缩影的图式流形进行同胚分类[2-4]的工作仅

限于比较小的自然数 n，而对以对轮图为缩影的图式流形进行同胚分类[5,6]的工作也限于比较小的自然数 n。

一般地，一个图式流形是由各种价杯的并构成的一个拓扑空间[1] 。目前学者最感兴趣的是以某简单图

为缩影的图式流形[7]。直观地说，以一个简单图



,GVE







,GVE为缩影的图式流形就是将 V中的每个顶点

v换成一个圆周，将 E中的每条边 e换成圆柱面





10,

S1所得到的 2维CW 复形，其中 2维CW 复形中的粘

附映射都是从圆周到圆周的同胚。因为粘附映射是同胚映射，所以粘附映射的映射度是 1或–1。又因为圆柱面





10,1

S的边界是两个圆周的不交并







S

S，所以相应的粘附映射





SS和的映



SS

*基金项目：浙江省自然科学基金资助项目(LY12A02002)。

#通讯作者。

平麟等  以对轮图为缩影图式流形的同胚类数

射度分别是 1



和2



，这里 1



，。



21,1







若，则称

12 1









S0,1是正边。若12 1





，则称





10,1

S是负边。这样，每一个图式流形都可以用一

个有向图来表示，而且把该有向图看作无向图就是简单图 G。

一个有向图(或图式流形)对应如下的 k阶方矩阵





b，其中





,,,

Vvv v，而且

1, ,

0, ,

i j













连接和的边是正边,

连接和的边是负边

没有边连接和

23n

我们称上述的 k阶方矩阵为相应的有向图(或图式流形)的伴随矩阵。

一个扭转变换就是将与某个顶点关联的所有粘附映射的定向反向，其它粘附映射的定向不变。由于一个图

式流形经过扭转变换后仍然与原来的图式流形同胚，所以可以通过若干个扭转变换将图式流形的极大树形中的

所有边都化成正边，使新得到的图式流形仍然与原来的图式流形同胚。

用集合来表示以简单图 G为缩影的所有图式流形。 G

对轮图共有 n个顶点和条边，其中 1n



个顶点和 2n



条边在圆周上依次相连围成一个圈，另一个

顶点在圆的中心，且圆周上的个顶点与中心相连正好有

1n1n



条边。下面以为例，给出缩影为对轮图

的所有图式流形的同胚分类。并且用 Burnside 引理[8,9]给出计算

W13

W13



的同胚类数的上界的一个方法。

2. 的同胚类数

W

在对轮图W(如图 1)中，由圆周上的 12 个顶点与中心相连的 12 条边组成一个极大树形，如图 2：

Figure 1. Round diagram Figure 2. Maximum tree of

W13

图1. 对轮图图2. 的极大树形

W13

通过若干次扭转变换将中图式流形的上述极大树形中的所有边都化成正边，不影响同胚类的类数。在

中，我们只假设所有负边正好有 k条，且都集中在圆周上的情形。



W

为了方便，设中 k条负边正好都集中在圆周上的同胚类数为，其中

k

m0k

W12



。根据不同的正边个数

和负边个数分 7种情形来考虑同胚分类：

情形 1 若，即所有边都是正边，这种情况只有 1种，因此0k01m



；根据图形的对称性，容易得 12 1m



。

情形 2 若时，则；同理可得k1

m111 1m



。 1

情形 3 若时，则有 2种情形： k2



3

情形 3.1 若两条负边相邻，则有 1个同胚类；

情形 3.2 若两条负边不相邻，则有 5个同胚类。

综上，。同理可得。

215m10 6m

情形 4 若时，有 3种可能的情形： k

情形 4.1 若3条负边相邻，则有 1个同胚类；

情形 4.2 若仅有 2条负边相邻，则有4个同胚类；

112

平麟等  以对轮图为缩影图式流形的同胚类数

情形 4.3 若3条负边两两不相邻，则有 7个同胚类。

综上，。同理可得。

314712m 912m

情形 5 若时，有 5种可能的情形： 4k

情形 5.1 若四条负边相邻，则有 1个同胚类；

情形 5.2 若仅有 3条负边相邻，则有4个同胚类；

情形 5.3 若有两组 2条负边相邻，但没有 2条以上的负边相邻，则有 4个同胚类；

情形 5.4 若其中仅有 2条负边相邻，另外的负边均不相邻，则有 12 个同胚类；

情形 5.5 若每 2条负边均不相邻，则有 8个同胚类。

综上，。同理可得

414412829m829m



。

情形 6 若时，有 7种可能的情形： 5k

情形 6.1 若5条负边相邻，则有 1个同胚类；

情形 6.2 若仅有 4条负边相邻，则有3个同胚类；

情形 6.3 若其中有 3条负边相邻，另2条负边也相邻，但没有 3条以上的负边相邻，则有 3个同胚类；

情形 6.4 若其中有 3条负边相邻，另2条负边均不相邻，则有 9个同胚类；

情形 6.5 若其中有 2组2条负边相邻，但没有 2条以上的负边相邻，则有 9个同胚类；

情形 6.6 若2条负边相邻，另 3条边均不相邻，则有 10 个同胚类；

情形 6.7 若每 2条负边均不相邻，则有 3个同胚类。

综上，。同理可得

513399103 38m 738m



。

情形 7 若时，有 11 种可能的情形： 6k

情形 7.1 若6条负边相邻，则有 1个同胚类；

情形 7.2 若仅有 5条负边相邻，则有3个同胚类；

情形 7.3 若其中有 4条负边相邻，另2条负边也相邻，但没有 4条以上的负边相邻，则有 3个同胚类；

情形 7.4 若4条负边相邻，另 2条负边均不相邻，则有 6个同胚类；

情形 7.5 若其中有 2组3条负边相邻，但没有 3条以上的负边相邻，则有 3个同胚类；

情形 7.6 若3条负边相邻，另 2条边相邻，但没有 3条以上的负边相邻，则有 10 个同胚类；

情形 7.7 若其中仅有 3条负边相邻，另外的负边均不相邻，则有 6个同胚类；

情形 7.8 若其中有 3组2条负边相邻，但没有 2条以上的负边相邻，则有 3个同胚类；

情形 7.9 若其中有 2组2条负边相邻，但没有 2条以上的负边相邻，则有 11 个同胚类；

情形 7.10 若其中只有2条负边相邻，另外的负边均不两两相邻，则有 3个同胚类；

情形 7.11 若任意 2条负边均不相邻，则有 1个同胚类。

综上，。

613363 10633 113 150m 

综合以上七种情况， 13



的同胚类数为

11612293850382912611224 .

定理 1 缩影为的所有图式流形的同胚类有 224 个。

W13

W

3. 的同胚类个数的下界

W

根据文献[4]提供的算法，用Matlab 软件求出伴随矩阵的特征多项式个数，就是以对轮图为缩影的图式

流形的同胚类个数。

W

第一步：利用 numtomatrix 函数，将一个数转化为矩阵，它只有一个矩阵编号，取值为 0到。得到形

如下的对称方阵：主对角线的元素为 0，其他元素是0,1,–1。

21

平麟等  以对轮图为缩影图式流形的同胚类数

0111111111111

10 000000000

100 00000000

1000 0000000

100000 00000

1000000 0000

10000000 000

1000000000 0

1 0000000000















































其中为 1或–1。 

第二步：计算矩阵的特征多项式。

第三步：用 select 函数去掉第二步中得到的特征多项式中相同的个数，得到共有 214 个不同的特征多项式，

即时，以对轮图为缩影的图式流形的同胚类下界为 214。 13n13

定理 2 具有缩影的图式流形的同胚类至少有 214 个。

4. 的同胚类数的上界

W

项链问题[8]：用 n种颜色的珠子做成有 m颗珠子的项链，问可以做成多少种不同类型的项链？

用m颗珠子做成一串项链，可以将一颗珠子看成一个顶点，则可以用正 m边形来表示项链。沿逆时针方向

对珠子进行标号。每颗珠子有n种颜色，则由乘法原理，这些有标号的项链有种。设



1,2, ,



m为m颗

珠子的集合，



,,,



aa a表示 n种颜色。 :



表示一个有标号的项链。令





 表示全部

有标号的项链的集合，则 m

n。但其中有些可以通过旋转一个角度或关于某条对称轴翻转后使之完全重合，

它们的本质是相同的。因此我们要考虑的是无论怎么旋转、翻转都不能使它们重合的项链的类型数。

正m边形的对称变换群为二面体群，记为，则

Dm。令 g对



的作用是项链的一次旋转变换或翻

转变换，则 m

D。现在将项链问题转化为找 g在



上的不动点个数

，即使得





的解的个数，这与

g的置换类型有关。设 g是一个 m



12 m





型置换，g的循环置换分解式表示为：























 



其中 12

12 m





 ，故不动点的个数

为12 m





。然后根据Burnside 引理，得到项链的种类

数为 12









。

而只要证明了旋转变化和翻转变换是同胚的，缩影为对轮图的图式流形



就可以看成是用 2种颜色的

珠子做成颗珠子的项链。 1n

定理 3 旋转变换和翻转变换是同胚的。

证明由于旋转变换是刚体运动，翻转变换是镜面反射，而刚体运动和镜面反射都是拓扑不变量，故旋转变

换和翻转变换都是同胚的。证毕。

以为例，即用2种颜色的珠子做成有 12颗珠子的项链，可以将其看成是正十二边形，沿逆时针方向

对12 颗珠子进行标号(如图3)。

13n

114

平麟等  以对轮图为缩影图式流形的同胚类数

12 11

321

Figure 3. Dodecagon with the label

图3. 有标号的正十二边形

第一类：旋转变换

1) 不动或者逆时针旋转 360˚：

 









































1123456789101112g；

2) 逆时针旋转 30˚：；



2123456789101112g

3) 逆时针旋转 60˚：







31357911 24681012g；

4) 逆时针旋转 90˚：







4147102581136912g；

5) 逆时针旋转 120˚：

 









515926103711 4812g；

6) 逆时针旋转 150˚：；



61 6 11 4927 1251038g

7) 逆时针旋转 180˚：















7172839410511612g；

8) 逆时针旋转 210˚：；



81 83105 127294 116g

9) 逆时针旋转 240˚：











91 952 106311 74128g；

10) 逆时针旋转 270˚：











10 110742118531296g；

11) 逆时针旋转 300˚：







11 111 97532 12 10864g；

12) 逆时针旋转 330˚：。



12 1121110987 65 432g

第二类：对称变换

1) 对称轴是连接 1、2珠子 7、8珠子的线段的中垂线：











 

13 123124115106978g；

2) 对称轴是连接 2、3珠子 8、9珠子的线段的中垂线：















 

14 23 14512611 71089g；

3) 对称轴是连接 3、4珠子 9、10 珠子的线段的中垂线：















 

15 3425 16712811 910g；

4) 对称轴是连接 4、5珠子 10、11 珠子的线段的中垂线：











 

16 45 3627 18 9121011g；

5) 对称轴是连接 5、6珠子 11、12 珠子的线段的中垂线：











 

17 56473829 1101112g；

6) 对称轴是连接 6、7珠子 12、1珠子的线段的中垂线：











 

18 67 58 49310 211112g；

7) 对称轴是连接 1、7珠子的直线：





























19 1 7212311410 5968g；

8) 对称轴是连接 2、8珠子的直线：





























20 2813 41251161079g；

9) 对称轴是连接 3、9珠子的直线：





























21 3924 15612711 810g；

10) 对称轴是连接 4、10 珠子的直线：





























22 410352617812911g；

11) 对称轴是连接 5、11 珠子的直线：





























23 511463728191012g；

12) 对称轴是连接 6、12 珠子的直线：





























24 612574839210111g。

其中型置换有 1个，每一个元素的不动点数为

112



；

12型置换有6个，每一个元素的不动点数为 25





；

2型置换有 7个，每一个元素的不动点数为 72





；

3型置换有 2个，每一个元素的不动点数为 22



；

4型置换有 2个，每一个元素的不动点数为 3



；

6型置换有 2个，每一个元素的不动点数为 2



；

12 型置换有4个，每一个元素的不动点数为 1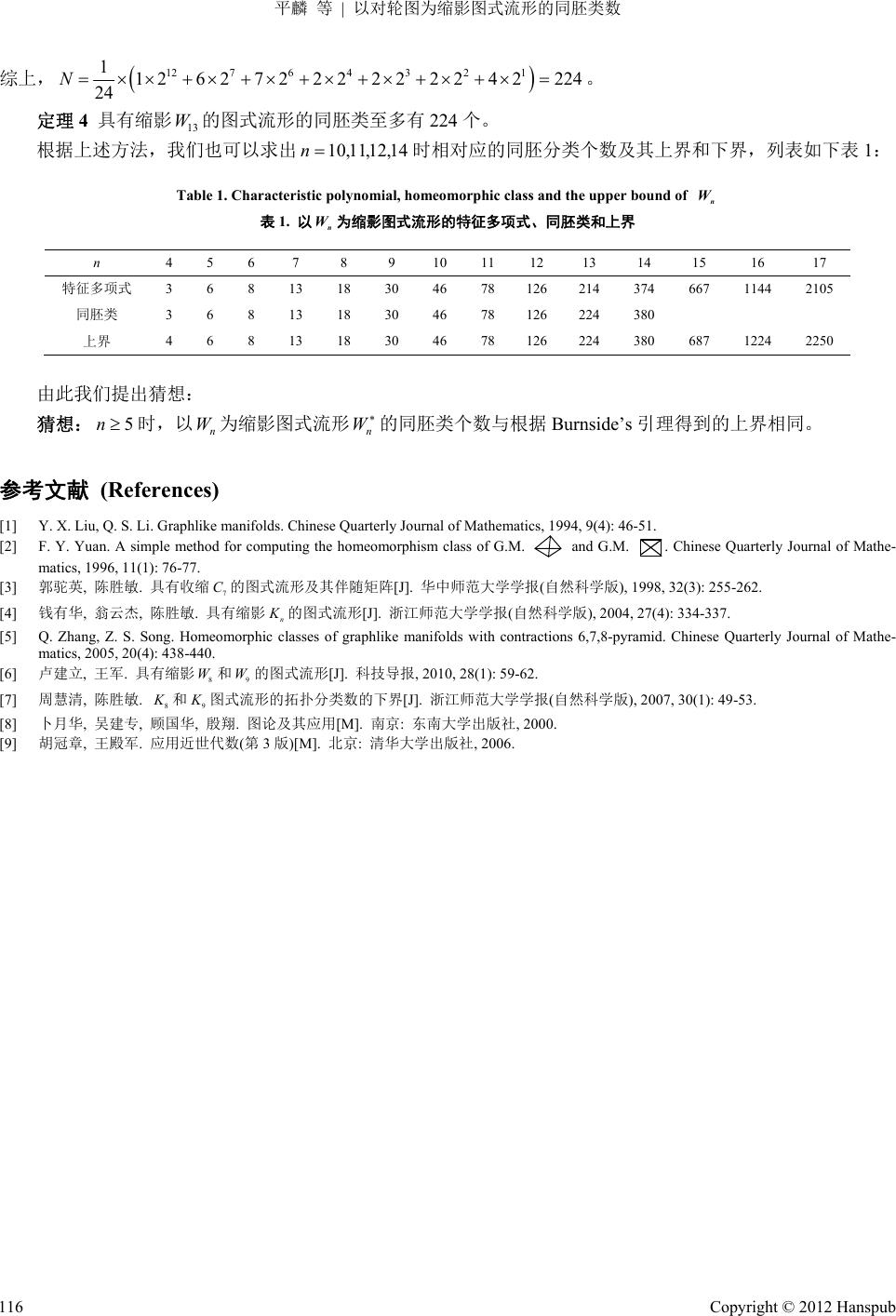



。

平麟等  以对轮图为缩影图式流形的同胚类数

116

综上，



12764321

11262 72 22 22 22 42224

N  。

定理 4 具有缩影的图式流形的同胚类至多有 224 个。

根据上述方法，我们也可以求出时相对应的同胚分类个数及其上界和下界，列表如下表 1： 10,11,12,14n

Table 1. Characteristic polynomial, homeomorphic class and the upper bound of

表1. 以为缩影图式流形的特征多项式、同胚类和上界

n 4 5 6 7 8 9 10 11 12 13 14 15 16 17

特征多项式 3 6 8 13 18 30 46 78 126 214 374 667 1144 2105

同胚类 3 6 8 13 18 30 46 78 126 224 380

上界 4 6 8 13 18 30 46 78 126 224 380 687 1224 2250

由此我们提出猜想：

猜想：时，以为缩影图式流形5nn



的同胚类个数与根据 Burnside’s引理得到的上界相同。

参考文献 (References)

[1] Y. X. Liu, Q. S. Li. Graphlike manifolds. Chinese Quarterly Journal of Mathematics, 1994, 9(4): 46-51.

[2] F. Y. Yuan. A simple method for computing the homeomorphism class of G.M. and G.M. . Chinese Quarterly Journal of Mathe-

matics, 1996, 11(1): 76-77.

[3] 郭驼英, 陈胜敏. 具有收缩 7

C的图式流形及其伴随矩阵[J]. 华中师范大学学报(自然科学版), 1998, 32(3): 255-262.

[4] 钱有华, 翁云杰, 陈胜敏. 具有缩影 n

的图式流形[J]. 浙江师范大学学报(自然科学版), 2004, 27(4): 334-337.

[5] Q. Zhang, Z. S. Song. Homeomorphic classes of graphlike manifolds with contractions 6,7,8-pyramid. Chinese Quarterly Journal of Mathe-

matics, 2005, 20(4): 438-440.

[6] 卢建立, 王军. 具有缩影 8

W和9

W的图式流形[J]. 科技导报, 2010, 28(1): 59-62.

[7] 周慧清, 陈胜敏. 8

和9

图式流形的拓扑分类数的下界[J]. 浙江师范大学学报(自然科学版), 2007, 30(1): 49-53.

[8] 卜月华, 吴建专, 顾国华, 殷翔. 图论及其应用[M]. 南京: 东南大学出版社, 2000.

[9] 胡冠章, 王殿军. 应用近世代数(第3版)[M]. 北京: 清华大学出版社, 2006.