Modeling and Simulation
Vol.
13
No.
02
(
2024
), Article ID:
83601
,
13
pages
10.12677/mos.2024.132178
45˚弯管和不同曲率90˚弯管的实验与数值模拟研究
贺浩1,刘冬华1,黄振华2,周传辉1
1武汉科技大学城市建设学院,湖北 武汉
2陕西大唐高科机电科技有限公司,陕西 西安
收稿日期:2024年1月11日;录用日期:2024年3月21日;发布日期:2024年3月29日

摘要
本文通过实验与数值模拟方法,对45˚弯管和不同曲率半径比(R/D = 1, 2, 3, 4, 5)的90˚弯管阻力系数进行了研究,分析了弯管内压力分布、速度矢量、二次流动及流动轨迹等规律,并重点分析了不同弯管曲率半径与管径之比下的弯管中流场流动特点。结果表明:RNG k-ε湍流模型的模拟结果与实验吻合较好。同一Re下,R/D越大局部阻力系数ξ越小,R/D在1~3范围内增大曲率可以明显降低局部阻力系数,再增大曲率局部阻力减小不明显。
关键词
45˚弯管,90˚弯管,阻力实验,数值模拟,曲率半径比,局部阻力系数ξ

Experimental and Numerical Simulation of 45˚ Bending and 90˚ Bending with Different Curvatures
Hao He1, Donghua Liu1, Zhenhua Huang2, Chuanhui Zhou1
1School of Urban Construction, Wuhan University of Science and Technology, Wuhan Hubei
2Shaanxi Datang Gaoke Electromechanical Technology Co., Ltd., Xi’an Shaanxi
Received: Jan. 11th, 2024; accepted: Mar. 21st, 2024; published: Mar. 29th, 2024

ABSTRACT
In this paper, the resistance coefficient of 45˚ bending pipe and 90˚ bending pipe with different ratio of curvature radius (R/D = 1, 2, 3, 4, 5) was studied by experimental and numerical simulation methods, and the laws of pressure distribution, velocity vector, secondary flow and flow trajectory in bending pipe were analyzed, and the characteristics of flow field in bending pipe with different ratio of curvature radius to diameter were emphatically analyzed. The results show that the simulation results of RNG k-ε turbulence model agree well with the experimental results. Under the same Re, the larger the R/D, the smaller the local drag coefficient. When R/D increases the curvature in the range of 1~3, the local drag coefficient can be significantly reduced, and when R/D increases the curvature, the local drag is not significantly reduced.
Keywords:45˚ Bending Pipe, 90˚ Bend Pipe, Resistance Test, Numerical Simulation, Curvature Radius Ratio, Local Resistance Coefficient ξ

Copyright © 2024 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
流体在弯管内的流动是管道流动的常见现象,广泛的应用于流体输配管网系统中。流体经过弯管时,不仅会发生边界层分离,形成旋涡区,减小流体流通面积,还会产生与主流方向正交的二次流,这些现象是导致弯管产生局部阻力损失的主要原因 [1] 。贺益英等 [2] 讨论了弯管局部阻力系数的影响因素及规律,解释了管内壁粗糙度影响局部阻力系数的原因。李涛等 [3] 利用实验与数值模拟方法,对90˚弯管阻力系数进行了研究,指出弯管对上游的影响最远至1~2倍管径,对下游的影响可达70倍管径。江山等 [4] 指出RNG k-ε湍流模型对具有二次流的湍流流动模拟结果与实验吻合较好,能准确反映弯管内部流态。孙业志等 [5] 指出随Re增大流体对于管道壁面的压力增大,管内压力损失也在增大,并且管道外壁面变化更加明显。饶永超等 [6] 得出不同曲率半径与直径之比对管内流速分布有较大影响,β由小增大时,内侧流速逐渐变小,应尽量使用β较大的弯头附件以降低对管道内壁的冲击。李静等 [7] 对不同雷诺数Re和不同半径比Rc/D下90˚圆弧弯管内的流体流动进行了数值模拟,得出同一Re下,Rc/D越大,局部阻力影响长度越短。局部阻力影响长度随Re的增大先减小后趋于定值,且Rc/D越小,局部阻力影响长度越延后趋于定值。杨少东等 [8] 针对大管径通风弯管,采用Fluent软件分别对管径450 mm、750 mm、1000 mm、1500 mm、2000 mm,不同曲率半径比的90˚弯管进行数值模拟,指出同一半径比下,局部阻力系数随管径增大而减小,但当管径大于1000 mm后,局部阻力系数随管径变化很小,几乎趋于不变值,同一管径下,半径比越小,局部阻力系数越大。但值华等 [9] 对不同雷诺数、不同相对弯曲半径、不同弯曲角度、不同管径的三维弯管进行数值模拟研究,表明阻力系ξ随着相对弯曲半径跟直径的增大呈多项式减小,随着弯曲角度呈线性增加,当相对弯曲半径增加到一定范围时,在弯曲角度大于π/4的情况下,角度的变化对二次流的影响不再明显。秦明坤等 [10] 探讨了几种雷诺数和不同曲率下弯管的压力损失和二次流影响,指出二次流强度随R/D减小和Re的增大而增加。王志伟等 [11] 研究了上升管内气液两相流通过90˚弯管后的流动演化特性,李俊宝等 [12] 探讨了两相介质流经弯头处引起的脉动流激力特性规律。郑斐等 [13] 研究了不同流速和弯曲角度对弯头腐蚀的影响。曹学文等 [14] 对90˚弯管内环状流流动特性进行了研究。随着计算流体力学CFD的不断发展,利用数值模拟方法来分析弯管局部损失已成为重要研究手段。本文针对DN50的镀锌钢管,采用FLUENT软件分别对不同曲率半径比(R/D = 1, 2, 3, 4, 5)的90˚弯管和45˚弯管进行数值模拟,并与实验值对比,分析了流体通过弯管时的流动特性、压力分布及二次流变化,提出了调整粗糙高度使模拟值与实验值吻合的方法,以期为流体输配管网设计选型及优化提供参考。
2. 实验方案与分析
2.1. 实验装置与方案
弯管阻力测量实验装置系统图(图1)如下,实验装置采用镀锌钢管,搭建出图2的实验装置,设备的主要技术指标如下:
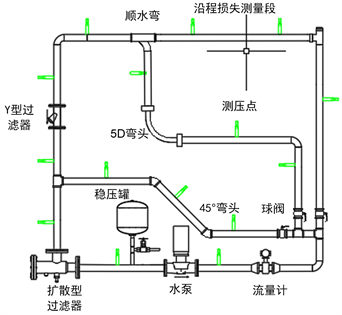
Figure 1. Bending resistance measuring device system
图1. 弯管阻力测量装置系统图

Figure 2. Bending resistance measuring device physical
图2. 弯管阻力测量装置实物图
立式离心泵:型号:IRG 50-100,流量:12.5 (m3/h),扬程:12.5 (m),电机功率:1.1 (kw);涡轮流量传感器:型号:LWGY-50,测量范围:2~20 (m3/h),精度0.5;压力传感器:型号:AE-3051,量程0~2 (kpa),精度0.15。
根据文献 [15] 的实测研究认为下游管段超过五倍当量直径对弯管局部阻力的测定基本上可满足要求。文献 [3] 认为弯管对管段上游的影响要比下游大得多,管段上游一般为1~2倍管径,下游则超过6倍管径。为此,根据实验条件,实验装置的测压孔在弯管上游满足超过3倍管径,下游超过6倍管径。因此,在局部构件上测得的全压差还包括了一部分直管段沿程损失,为了从实测中减去直管段损失还设置了一段沿程阻力损失测量管段。对于不同曲率半径的弯管,以5D弯管尺寸为标准,1~4D弯头各焊接一段短管以达到和5D弯头安装尺寸一致,采用卡盘–卡箍式连接以便替换。
2.2. 实验结果与分析
根据Darcy-Weisbach公式,有:
(1)
(2)
式中:pf为沿程阻力,pm为局部阻力,pa;λ为沿程阻力系数;ξ为局部阻力系数;L为管长,m;D为管径,m;v为断面平均流速,m/s;ρ为流体密度,kg/m3。
通过实验测得各个阻力部件在不同流速下的局部阻力损失,由式(1)得出沿程阻力系数λ,再计算得到局部阻力损失系数ξ,图3为几种弯管实物图,图4为1~5D弯管和45˚弯管局部阻力损失系数随雷诺数变化的实验值,初步分析实验结果得出,随着曲率半径比的增加,局部阻力系数逐渐减小,但减小幅度逐渐放缓,曲率半径比达到4D之后再增加曲率阻力系数减小幅度很小;针对DN50的镀锌钢管,45˚弯管阻力与3D曲率弯管十分接近,可以用大曲率弯管替换来节省安装尺寸。

Figure 3. Pipe bending
图3. 弯管实物图

Figure 4. Local drag loss coefficient
图4. 局部阻力损失系数图
3. 模拟计算与分析
3.1. 几何模型
物理模型为圆弧弯曲管道,由上游直管段、弯曲段和下游直管段组成。管直径D = 53 mm,半径比分别为1、2、3、4、5。为排除入口处流体不稳定性对计算结果影响和弯曲段对下游直管段的影响,上下游直管段长度取L = 10D,如图5所示。
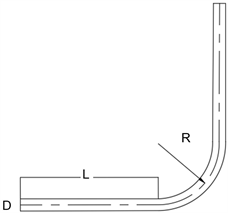
Figure 5. Bending pipe geometry model
图5. 弯管几何模型图
3.2. 网格划分及湍流模型
网格划分采用六面体网格,转弯处采用非结构四面体网格,并进行网格加密,如图6所示,以2D弯管为例,验证不同网格密度对局部阻力系数ξ的影响,由图7可以看出,当网格数为803,723时,计算结果与网格数为1,899,741时十分接近,最大相对误差仅为0.91%,增加网格数量时局部阻力系数无明显变化,考虑计算精度与模拟时间,采用网格数为803,723的网格密度进行模拟,其他弯管也采用此方法进行选取。本次模拟工质为水,在常温下为不可压缩流体,根据董亮 [16] 等人的研究表明采用RNG k-ε模型计算的结果与实验值更为接近,取2D弯管的实验数据与三种模拟数据进行对比,图8为对比结果,由图可知三种模型中,RNG k-ε模型模拟值与实验值吻合最好,全部误差在10%以内,说明此模型的模拟具有可靠性。
3.3. 求解方法与边界条件
采用三维稳态模型进行求解,流场设置基于压力修正法的SIMPLE算法迭代计算,采用二阶迎风格式对方程进行离散,残差收敛值设为10−6,迭代步长设置为1000步,壁面设置无滑移边界条件,近壁面的处理采用标准壁面函数法。弯管进口边界条件为速度进口,取值与实验值相同,出口设置为自由出流,通过调整壁面粗糙高度来与实验值拟合。

Figure 6. Meshing diagram
图6. 网格划分图
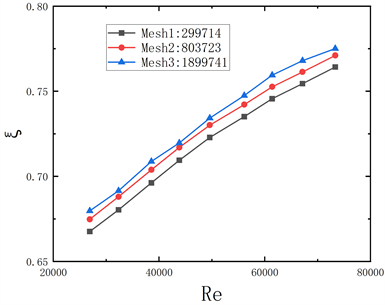
Figure 7. The influence of mesh density on the calculation results
图7. 网格密度对计算结果的影响
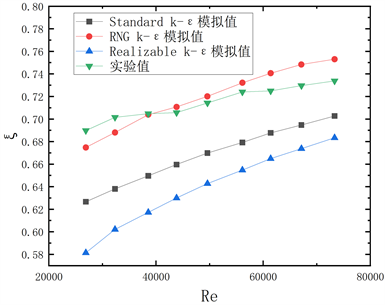
Figure 8. Experimental values and simulated values
图8. 实验值与几种模型的模拟值
3.4. 模拟结果与分析
3.4.1. 压力分布与速度分布
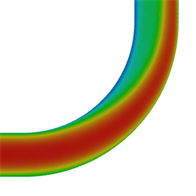
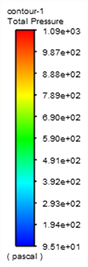
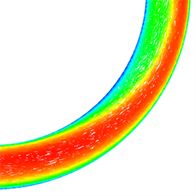
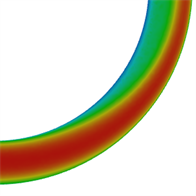
图9为v = 1 m/s时,不同曲率90˚弯管和45˚弯管的管道对称中心截面上压力和速度分布云图。从图中可以看到,水流通过弯管时流速和压力分布沿程不断调整。在弯管进口处,靠近内壁面区域流体速度增大,压力减小,而外壁面附近区域流体速度减小压力增大,在出口处压力与速度分布则与进口处分布规律相反。这是由于弯管的几何形状导致的流体流动发生了弯曲和转动,产生了离心力和切向应力,使得流体在不同位置具有不同的速度和压力分布。在弯管进口处靠近内壁面区域,由于流体需通过弯曲区域,速度会增大以保持质量守恒,同时在受到离心力的作用下,流体靠近内侧壁面运动速度加快。而在外壁面附近,由于受到离心力的影响减小,运动速度相应下降,同时由于弯管与直管连接处的关系,液体流向管中心会收缩,从而压力在此处增大。最后,在出口处,流体通过弯管后速度和压力的分布势必与进口处相反,因为流体需恢复到对流态的状态。这些特性使得弯管成为液体输送和流动控制中一个有效的结构。同时可以看到,同一Re下,曲率半径越小,弯管内压力和速度梯度变化越大,这是由于曲率半径越小流体收到的惯性力和离心力越强所致。
3.4.2. 二次流分析
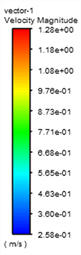
图10是2D弯管在速度为1 m/s下的弯曲管段分别取θ = 0˚,30˚,60˚,90˚时以及下游直管段L = 5 d和10 d截面处的速度矢量图,从图中可以看出流体在弯管处二次流的形成与发展过程,在θ = 0˚的进口截面,水流径向速度都指向内壁面,这是由于此处径向压力梯度所致,在θ = 30˚时,由于外壁面附近压力大于内壁面附近压力,使得外壁面附近的流体向上下流动,内壁面附近的流体向内流动从而产生二次流,在θ = 60˚截面处二次流达到最大,在θ = 90˚截面处仍有二次流现象,这会影响下游直管段一定范围内的紊流现象,从L = 5 d和10 d处截面图可以看出二次流逐渐减小,对压力影响逐步减小。因此取5 d出为测点压力影响基本可以忽略。流体进入90˚圆弧弯管时,由于压力和速度的综合变化,使得外壁面出现扩散效应,内壁面出现收缩效应,在弯管内壁面附近产生涡流区;流体流出90˚圆弧弯管时,弯管内外壁面的压力和速度开始向相反的方向变化,使得弯管外壁附近产生涡流区。




(a1) 1D Pressure nephogram (a2) 1D Velocity vector diagram
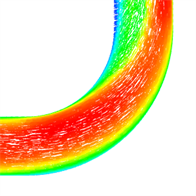
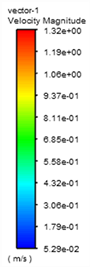

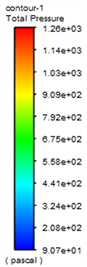
(b1) 2D Pressure nephogram (b2) 2D Velocity vector diagram


(c1) 3D Pressure nephogram (c2) 3D Velocity vector diagram
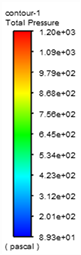
(d1) 4D Pressure nephogram (d2) 4D Velocity vector diagram
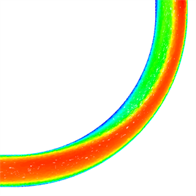
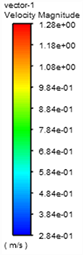

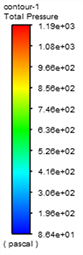 (e1) 5D Pressure nephogram (e2) 5D Velocity vector diagram
(e1) 5D Pressure nephogram (e2) 5D Velocity vector diagram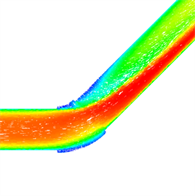


 (f1) 45˚Pressure nephogram (f2) 45˚Velocity vector diagram
(f1) 45˚Pressure nephogram (f2) 45˚Velocity vector diagram
Figure 9. Pressure distribution and velocity distribution of the center section of different bent pipes
图9. 不同弯管管道中心截面的压力分布图与速度分布图

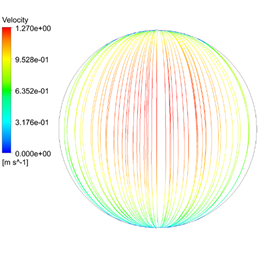
θ = 0˚ θ = 30˚
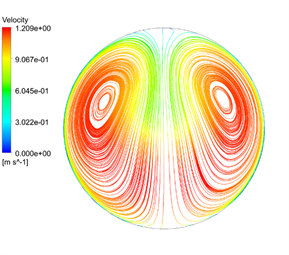
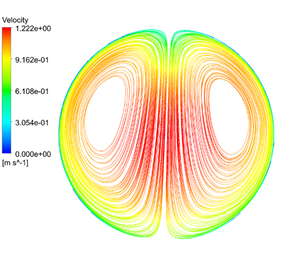 θ = 60˚ θ = 90˚
θ = 60˚ θ = 90˚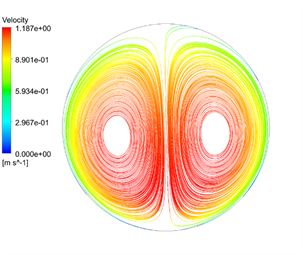
 L = 5D L = 10D
L = 5D L = 10D
Figure 10. Secondary flow in different sections of curved pipe section and different sections of downstream pipe
图10. 弯曲管段不同截面和下游管段不同截面的二次流
(a) 45˚ bend (b) 1D bend
 (c) 2D bend (d) 3D bend
(c) 2D bend (d) 3D bend
 (e) 4D bend (f) 5D bend
(e) 4D bend (f) 5D bend
Figure 11. The fitting of simulated values and experimental values with different rough heights
图11. 不同粗糙高度模拟值与实验值的拟合
3.4.3. 粗糙高度对模拟结果的影响
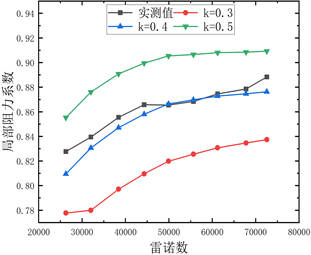
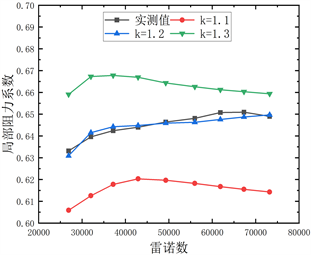
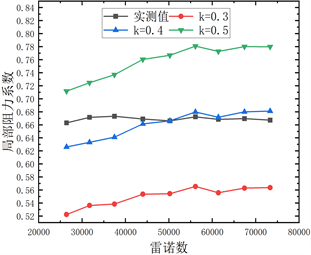
通过数值模拟的方法可以模拟出常规实验无法得到的不同流场的各种信息,相关的研究对于粗糙高度往往按手册选取k = 0.15 mm [17] ,在本实验中并不能很好的拟合实验值,故考虑与实验值准确拟合,本模拟通过调整粗糙高度来改变模拟结果,此方法可以使结果趋近实验值,图11为本实验中几种弯管的模拟值与实验值对比,由图可知,1~5D弯管,取k = 0.4均能较好的拟合实验值,全部误差不超过10%,可以认为模拟具有准确性,针对45˚弯管粗糙高度达到了1.2,初步分析不一致的原因可能与弯头形状与连接方式有关。
为找出45度弯管粗糙高度不一致的原因,针对模型做进一步调整,由于大曲率弯头采用的是卡盘连接,接口处较为平滑,而45˚弯管采用的是螺纹连接,两端连接处实际上存在一个很小的突扩突缩,测量实物后将模型调整为带突扩突缩的弯头,如图12所示,再次模拟得到图13结果,由图可知,粗糙高度取0.4可以很好的拟合实验值,与其它几种弯管模拟所取的粗糙高度一致,进一步证实了采用RNG k-ε模型计算与实验对比的准确性。
Figure 12. 45˚ bending model with sudden expansion and contraction
图12. 加突扩突缩的45˚弯管模型
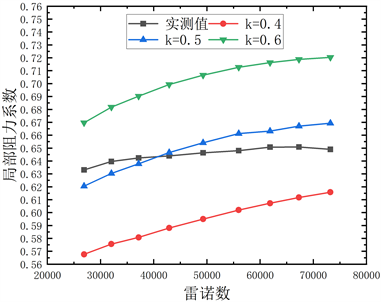
Figure 13. The simulated value of 45˚ bend with sudden expansion and contraction
图13. 加突扩突缩的45˚弯管模拟值
4. 结论
针对DN50的镀锌钢管,分别采用了实验和模拟的方法,对45˚弯管和不同半径比(R/D = 1, 2, 3, 4, 5)的90˚弯管进行研究,分析了流体通过击中弯头时的流动特性,探讨了弯管局部阻力产生的主要原因,研究了不同曲率弯头的局部阻力系数,旨在为相关工程设计提供一定参考价值,得出如下结论:
1) 对于实验与模拟的拟合方法,采用RNG k-ε模型模拟较为可靠,可以很好地模拟紊流过渡区流场特性。
2) 通过调整粗糙高度的方法,可以使模拟值较好地与实验值吻合,此方法可以找出管道最佳粗糙高度拟合值,再以此来模拟其他工况。
3) 针对螺纹连接的45˚弯管,可采用3D曲率弯管替换以节省安装尺寸,两者的局部阻力损失接近。
4) 对于相同管径和流速,弯管局部阻力系数随着曲率半径比R/D的增大而减小,1~3D范围内变化显著,继续增大曲率半径局部阻力系数降低很小。
文章引用
贺 浩,刘冬华,黄振华,周传辉. 45°弯管和不同曲率90°弯管的实验与数值模拟研究
Experimental and Numerical Simulation of 45° Bending and 90° Bending with Different Curvatures[J]. 建模与仿真, 2024, 13(02): 1908-1920. https://doi.org/10.12677/mos.2024.132178
参考文献
- 1. 王松岭. 流体力学[M]. 北京: 中国电力出版社, 2007.
- 2. 贺益英, 赵懿珺, 孙淑卿, 毛世民. 弯管局部阻力系数的试验研究[J]. 水利学报, 2003(11): 54-58.
- 3. 李涛, 李安桂, 周艳. 通风空调低雷诺数90˚弯管阻力系数的实验与数值模拟[J]. 青岛科技大学学报(自然科学版), 2006(6): 527-531.
- 4. 江山, 张京伟, 吴崇健, 许清, 彭文波. 基于FLUENT的90˚圆形弯管内部流场分析[J]. 中国舰船研究, 2008(1): 37-41.
- 5. 孙业志, 胡寿根, 赵军, 仲志刚. 不同雷诺数下90˚弯管内流动特性的数值研究[J]. 上海理工大学学报, 2010, 32(6): 525-529. https://doi.org/10.13255/j.cnki.jusst.2010.06.011
- 6. 饶永超, 常凯, 王树立, 李建敏, 杨敏官, 杭越. 90˚弯管内流体流动特点数值模拟[J]. 常州大学学报(自然科学版), 2016, 28(3): 65-69.
- 7. 李静, 杨俊红, 黄涛, 韩奎, 高琳. 雷诺数和半径比对90˚圆弧弯管流动特性的数值研究[J]. 机械科学与技术, 2017, 36(10): 1491-1497. https://doi.org/10.13433/j.cnki.1003-8728.2017.1003
- 8. 杨少东, 肖瑶, 侯京婧, 魏刚. 大管径90˚弯管数值模拟及局部阻力特性研究[J]. 能源与节能, 2020(8): 133-136. https://doi.org/10.16643/j.cnki.14-1360/td.2020.08.057
- 9. 但植华, 吴森林, 管英柱, 纪国法, 张金发, 陈菊. 基于CFD的弯管数值计算及水力特性分析[J]. 中国测试, 2023, 49(3): 142-151.
- 10. 秦明坤, 李强, 王建普. 90˚弯管内流动特性数值研究[J]. 化工生产与技术, 2020, 26(1): 11-14 17 7-8.
- 11. 王志伟, 何炎平, 李铭志, 等. 基于计算流体力学的90˚弯管气液两相流数值模拟及流型演化[J]. 上海交通大学学报, 2022, 56(9): 1159-1167. https://doi.org/10.16183/j.cnki.jsjtu.2021.185
- 12. 李俊宝, 王泽武, 胡佳顺, 等. 气液两相流管道弯头处脉动流激力特性研究[J]. 化学工程, 2023, 51(4): 45-50, 67.
- 13. 郑斐, 邢少华, 何华, 等. 流速和弯曲角度对弯头腐蚀行为影响仿真研究[J]. 装备环境工程, 2020, 17(6): 18-23.
- 14. 曹学文, 李相, 张磐, 等. 90˚水平弯管内环状流流动特性[J]. 油气储运, 2023, 42(1): 54-63. https://doi.org/10.6047/j.issn.1000-8241.2023.01.008
- 15. 汪兴华, 吴德怀. 风管标准弯头和变径管的局部阻力试验[J]. 暖通空调, 1981(1): 22-26.
- 16. 董亮, 刘厚林, 代翠, 等.不同湍流模型在90˚弯管数值模拟中的应用[J]. 华中科技大学学报(自然科学版), 2012, 40(12): 18-22.
- 17. 陆耀庆. 实用供热空调设计手册[M]. 北京: 中国建筑工业出版社, 2008: 1100.