考虑历史洪水资料的EMA参数估计方法 EMA Parameters Estimation Method with Consideration of Historical Flood Information

doi:10.12677/JWRR.2012.14037

设为首页加入收藏期刊导航网站地图

期刊菜单

文章导航

Journal of Water Resources Research 水资源研究, 2012, 1, 256-261

http://dx.doi.org/10.12677/jwrr.2012.14037 Published Online August 2012 (http://www.hanspub.org/journal/jwrr.html)

EMA Parameters Estimation Method with Consideration

of Historical Flood Information*

Junzhen Wang, Songbai Song

College of Water Resources and Architectural Engineering, Northwest A&F University, Yangling

Email: junzicau@yahoo.com.cn, ssb6533@nwsuaf.edu.cn

Received: Jun. 21st, 2012; revised: Jul. 2nd, 2012; accepted: Jul. 9th, 2012

Abstract: In order to more efficiently use historical information and improve the precision of distribution

parameter estimates of historical flood information, this paper summarized the method of using expected

moments algorithm (EMA) to calculate flood quantile estimates when historical flood information is avail-

able. Based on EMA principle, an annual peak discharge data with P-III type distribution was employed to

illustrate to parameters estimation of the distribution, the annual peak discharge frequency curve with the

estimated parameters was given. Comparing with traditional methods, the results show that all the three

method’s results are similar and close to empirical probabilities for lower floods segment, but in the large

floods segment, EMA is the closest to empirical probabilities. It also indicates that EMA has considerable

merit in the P-III type distribution of flood frequ ency parameter estimation when historical flood information

is available and has higher precision.

Keywords: Flood Frequency Analysis; P-III Type Distribution; EMA Parameter Estimation Method

考虑历史洪水资料的 EMA 参数估计方法*

王俊珍，宋松柏

西北农林科技大学水利与建筑工程学院，杨凌

Email: junzicau@yahoo.com.cn, ssb6533@nwsuaf.edu.cn

收稿日期：2012 年6月21 日；修回日期：2012 年7月2日；录用日期：2012 年7月9日

摘要：为了更有效地应用历史资料信息，提高具有历史洪水资料序列参数的估计精度，研究expected

moments algorithm (EMA)法进行具有历史洪水资料的参数估计方法。本文在介绍EMA 原理的基础上，

以实测洪峰序列为例，选用 P-III 型分布，进行年最大洪峰序列拟合分布的参数估计，并根据估计参数

推求洪峰流量频率曲线图。与传统参数估计方法比较，结果表明：大洪水段，EMA最接近经验点据，

而在一般洪水序列段中，三种方法拟合结果相差不大，大部分与实测值接近。因此，在考虑历史洪水

的情形下，EMA 能有效地进行P-III 型分布参数估计，且较传统方法精度高。

关键词：洪水频率分析；P-III 型分布；EMA 参数估计方法

1. 引言

历史洪水在设计洪水计算中起着非常重要的作

用。P-III 型分布是我国水文分析计算推荐使用的线

型，国内外水文工作者对其参数估计问题进行了大量

的研究[1]。矩法有较大的估计偏差，尤其是对 Cs 的估

计。丁晶、宋德敦等[2]在Greenwood(1979)定义的概率

权重矩的基础上，提出了 P-III 型分布参数估计的概率

*基金项目：国家自然科学基金(51179160，50879070，50579065)；

高等学校博士学科点专项科研基金(20110204110017)。

作者简介：王俊珍(1987-)，女，贵州凯里人，在读硕士生，主要

从事流域水文模拟及水文预报研究。

256

王俊珍，等：考虑历史洪水资料的 EMA 参数估计方法

第1卷 · 第4期

权重矩数值计算法，该法具有良好的不偏性，但对于

Cs 的抽样误差较大，尤其是短序列。马秀峰[3]于1984

年提出了权函数法，在样本矩的计算中引入正态概率

密度函数作为权函数，增加了靠近均值部分的权重，

减小了两端部分的权重，从而减小“矩差”，提高了

Cs 的估计精度，但是权函数属于单参数估计，不能全

面地解决P-III 型分布水文频率参数估计问题，包括均

值，特别是 Cv 的估计精度问题[4]。刘光文[5]于1990

年提出数值积分双权函数法，引入两个权函数，并采

用数值积分公式计算权重函数矩，以提高计算精度，

特别是 Cv 的精度，但该法计算比较复杂。Hosking[6]

在Greenwood(1979)定义概率权重矩之后，于 1990 年

提出了线性矩，该法是概率权重矩的线性组合，其最

大特点是对洪水系列中的极大值和极小值远没有常

规矩那么敏感，所以估计结果受样本中个别点据误差

的影响较小，但该法以概率作为权重来求矩的，在各

阶矩中，变数均为一次幂，其阶次主要由其相应的概

率(作为权重)来反映，在推求参数时会引起误差和灵

敏性问题[7]。

Cohn[8]于1997 年提出了 EMA(Expected Moments

Algorithm)算法，该法的主要思想是在具有历史洪水

的情形下，以矩法估计结果为初值，充分考虑小于门

限值 T(一般认为很大的洪峰流量)的洪水资料，通过

高效迭代去提高洪水分位点估计，以提高估计精度和

收敛速度，迭代次数一般少于 10 次。本文选用 P-III

型分布，在介绍 EMA 的原理和算法的基础上，并将

其应用于具有历史洪水的洪水序列参数估计实例中，

并与矩法和线性矩法进行了比较分析。

2. EMA原理与算法

2.1. EMA原理

在实测资料系列外，当调查到若干次历史洪水，或

实测资料系列中出现特大洪水，经资料考证，需做特

大值处理时，均会使得实测或调查的特大洪水值应在

远较实测资料更长的时期内进行排序，这就构成了不

连序系列样本[9]。由于对不连序系列样本的传统参数估

计方法，分别源于连序样本估计方法，故传统估计方

法所存在的问题也都依然存在[2]。EMA 是基于矩法进

行不连序系列样本“洪水”频率分析的参数估计方法。

首先，由实测资料计算 EMA 的初始矩，然后在

此基础上由实测洪峰流量、期望矩和历史洪水期中小

于T的特大洪水年限 he





进行修正，得到新的估计

参数，重复以上步骤，直到估计参数收敛。图 1为洪

水序列示意图，图中阴影部分为历史洪水期小 T的未

知洪水 he





，e



表示历史洪水期中大于 T的特大洪水

个数，e表示在实测期中大于 T的特大洪水个数。

2.2. EMA算法

EMA 的算法过程数学描述如下[8,10]。

2.2.1. 样本矩初始估计

P-III 型分布的概率密度函数为

Figure 1. Flood records with both historical and systematic data

图1. 洪水序列

王俊珍，等：考虑历史洪水资料的 EMA 参数估计方法

第1卷 · 第4期



exp

,,, 0

,,0, 0

xa xa

fx a





  

 





 



 



 

















(1)

式中， 0





，，分别为 P-III 型分布的形状、尺度和

位置参数，其中，完全gamma 函数为



tet







 (2)

利用矩法计算 P-III 型分布洪峰流量序列的参数

公式如下：















(3)

 

211

ˆˆ

ˆ1

iik











 







(4)

 

 

ˆˆ

iik

Nx x

cNN













 











(5)

式中：分别表示历史考证期长度、第i个

洪峰流量、特大洪水个数、实测洪水资料和发生在实

测期的特大洪水个数。符号“”表示参数估计值。

P-III 型分布的参数可以通过式(6)~(8)进行求解。

,,,,

Nx kse



ˆˆS



 (6)



ˆˆ

sign ˆ











(7)

0ˆ

ˆˆ





 (8)

2.2.2. 计算 EMA 矩

1) 利用初始矩来计算。

1101

ˆˆ1, 2

ii i





, , ,

ˆˆ



 (9)



ˆˆ

sign ˆi

iSi













(10)

011 1

ˆˆ

iii









 (11)

2) 利用新的参数来求解样本矩 11

ˆˆˆ

iiSi





 

，计

算公式为





ii h

iik

xxheEx















 e

(12)

式中：





,, ,

heh e

hexE x







分别表示历史洪水期、历史

期的特大洪水个数、历史洪水期中洪峰流量小于 T的

流量和





的期望矩，可用不完全 gamma 函数



来表示，

Exa axa





 

















 







(13)



0exp d





 

t

(14)





11 -

211

ˆˆ

iiiihe i

iik

xxheEx

























  











 (15)

式中：C2为偏态修正系数。

Cse











 (16)





31 1-

131

ˆˆ ˆ

ˆˆ

iiiihe i

iik

cxx heEx



























  











 (17)

式中：C3为相应的偏态修正系数。

258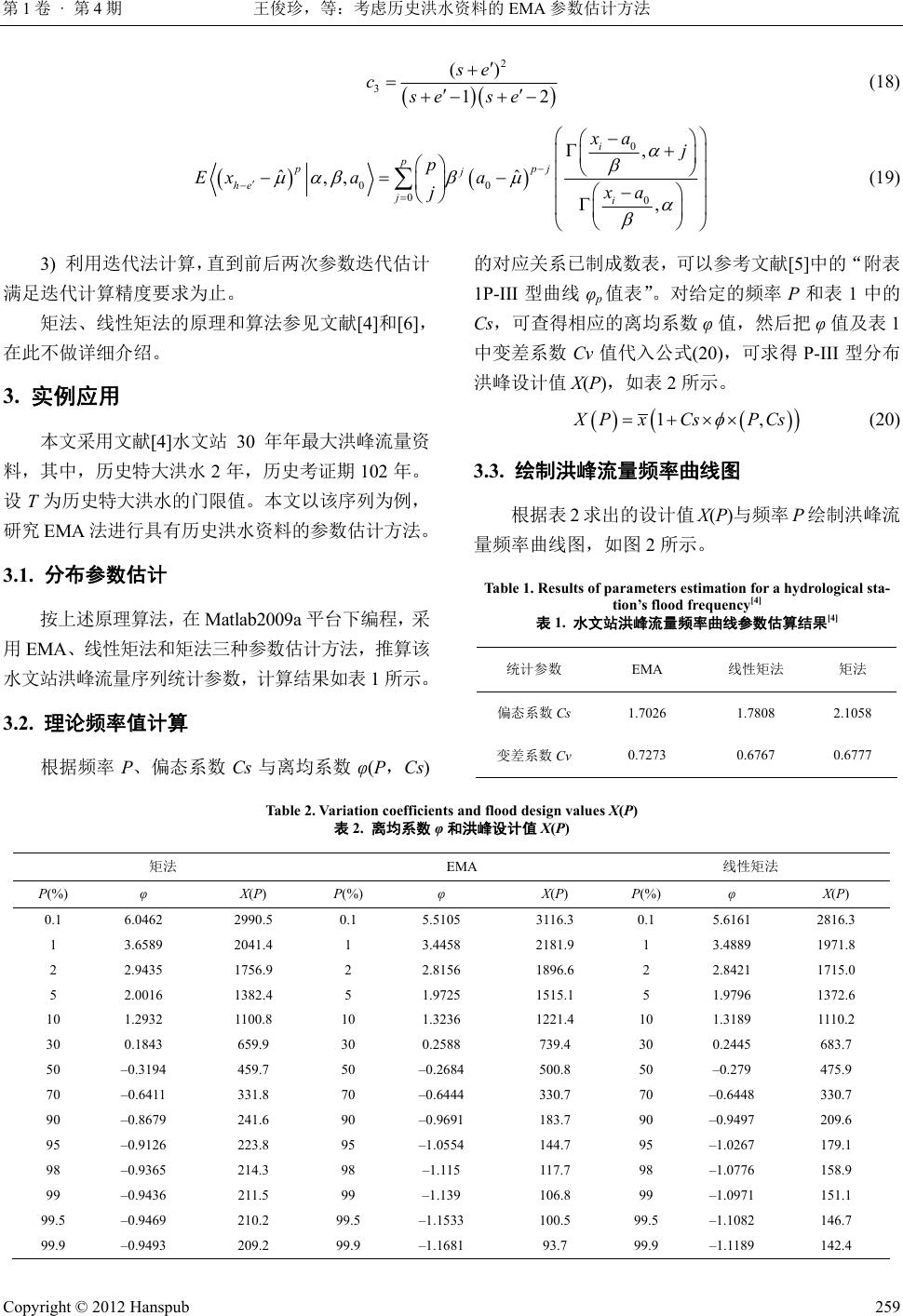

王俊珍，等：考虑历史洪水资料的 EMA 参数估计方法

第1卷 · 第4期

 

3()

cse se











(18)

 

ˆˆ

ppj

xa j

Ex aa

jxa





 





















 





 





 









(19)

3) 利用迭代法计算，直到前后两次参数迭代估计

满足迭代计算精度要求为止。

矩法、线性矩法的原理和算法参见文献[4]和[6]，

在此不做详细介绍。

3. 实例应用

本文采用文献[4]水文站 30 年年最大洪峰流量资

料，其中，历史特大洪水 2年，历史考证期 102 年。

设T为历史特大洪水的门限值。本文以该序列为例，

研究 EMA 法进行具有历史洪水资料的参数估计方法。

3.1. 分布参数估计

按上述原理算法，在 Matlab2009a 平台下编程，采

用EMA、线性矩法和矩法三种参数估计方法，推算该

水文站洪峰流量序列统计参数，计算结果如表 1所示。

3.2. 理论频率值计算

根据频率 P、偏态系数Cs 与离均系数 φ(P，Cs)

的对应关系已制成数表，可以参考文献[5]中的“附表

1P-III 型曲线 φp值表”。对给定的频率P和表1中的

Cs，可查得相应的离均系数φ值，然后把φ值及表 1

中变差系数 Cv值代入公式(20)，可求得 P-III 型分布

洪峰设计值X(P)，如表 2所示。









Px CsPCs



 (20)

3.3. 绘制洪峰流量频率曲线图

根据表 2求出的设计值 X(P)与频率 P绘制洪峰流

量频率曲线图，如图 2所示。

Table 1. Results of parameters estimation for a hydrological sta-

tion’ s flood frequency[4]

表1. 水文站洪峰流量频率曲线参数估算结果[4]

统计参数 EMA 线性矩法矩法

偏态系数 Cs 1.7026 1.7808 2.1058

变差系数 Cv 0.7273 0.6767 0.6777

Table 2. Variation coefficients and flood design values X(P)

表2. 离均系数 φ和洪峰设计值 X(P)

矩法 EMA 线性矩法

P(%) φ X(P) P(%) φ X(P) P(%) φ X(P)

0.1 6.0462 2990.5 0.1 5.5105 3116.3 0.1 5.6161 2816.3

1 3.6589 2041.4 1 3.4458 2181.9 1 3.4889 1971.8

2 2.9435 1756.9 2 2.8156 1896.6 2 2.8421 1715.0

5 2.0016 1382.4 5 1.9725 1515.1 5 1.9796 1372.6

10 1.2932 1100.8 10 1.3236 1221.4 10 1.3189 1110.2

30 0.1843 659.9 30 0.2588 739.4 30 0.2445 683.7

50 –0.3194 459.7 50 –0.2684 500.8 50 –0.279 475.9

70 –0.6411 331.8 70 –0.6444 330.7 70 –0.6448 330.7

90 –0.8679 241.6 90 –0.9691 183.7 90 –0.9497 209.6

95 –0.9126 223.8 95 –1.0554 144.7 95 –1.0267 179.1

98 –0.9365 214.3 98 –1.115 117.7 98 –1.0776 158.9

99 –0.9436 211.5 99 –1.139 106.8 99 –1.0971 151.1

99.5 –0.9469 210.2 99.5 –1.1533 100.5 99.5 –1.1082 146.7

99.9 –0.9493 209.2 99.9 –1.1681 93.7 99.9 –1.1189 142.4

王俊珍，等：考虑历史洪水资料的 EMA 参数估计方法

第1卷 · 第4期

Figure 2. Hydrological station’s flood frequency plot[4]

图2. 水文站洪峰流量频率曲线图[4]

参考文献 (References)

由图 2看出，在两个历史特大洪水位置处，EMA

最接近经验点据，矩法其次，线性矩法离得最远，而

在一般洪水序列的洪水拟合中，三种方法拟合结果相

差不大，大部分与实测值接近。所以，从整体拟合的

结果看出，EMA 可以应用于洪水频率分布的参数估

计，且在考虑历史洪水时，EMA 较矩法和线性矩法

更为优越。

4. 结论

本文对比分析了EMA、线性矩和矩法的计算结

果，表明 EMA 法是一种简单和高效的不连序样本洪

水频率参数估算方法。与传统的线性矩和矩法相比，

EMA 能更高效地利用大值洪水资料。但是 EMA 的应

用需注意不连序样本区分实测特大洪水值和特大洪

水个数，要确保它们的质量。此外，在今后 EMA 算

法的研究过程中，需要对不连序洪水样本中的异常值

以及置信区间设定进行进一步地研究。

5. 致谢

本文系国家自然科学基金(51179160，50879070，

50579065) 和高等学校博士学科点专项科研基金

(20110204110017) 资助。在研究过程中，作者十分感

谢T imothy A. Cohn博士给予的指导和文献资料。

[1] 周芬, 郭生练, 肖义, 等. P-III型分布参数估计方法的比较研

究[J]. 水电能源科学, 2003, 21(3): 10-13.

ZHOU Fen, GUO Shenglian, XIAO Yi, et al. Co mparative study

on parameter estimation methods of Pearson type III distribution .

Water Resource and Power, 2003, 21(3): 10-13. (in Chinese)

[2] 丁晶, 宋德敦, 杨荣富. 估计P-III 型分布新方法——概率权

重矩法[J]. 成都科技大学学报, 1988, 2: 12-18.

DING Jing, SONG Dedun and YANG Rongfu. New method for

estimating P-III distribution—Probability-weighted moment.

Journal of Chengdu University of Science and Technology, 1988,

2: 12-18. (in Chinese)

[3] 马秀峰. 计算水文频率参数的权函数法[J]. 水文, 1984, 3: 1-

11.

MA Xiufeng. Weight function method for calculating hydro-

logical frequency parameters. Hydrology, 1984, 3: 1-11. (in Chi-

nese)

[4] 叶守泽, 詹道江. 工程水文学[M]. 北京: 中国水利水电出版

社, 2000.

YE Shouze, ZHAN Daojiang. Engineering hydrology. Beijing:

China Water Power Press, 2000. (in Chinese)

[5] 刘光文. 皮尔逊 III型分布参数估计[J]. 水文, 1990, 4-5: 1-15.

LIU Guangwen. Para meter estimation of Pearson type III distri -

bution. Hydrology, 1990, 4-5: 1-15. (in Chinese)

[6] 陈元芳, 沙志贵, 陈剑池, 等. 具有历史洪水时 P-III 分布线

性矩法的研究[J]. 河海大学学报, 2001, 29(4): 76-80.

CHEN Yuanfang, SHA Zhigui, CHEN Jianchi, et al. Study on

L-moment estimation method for P-III distribution with histori-

cal flood. Journal of Hohai University, 2001, 29(4): 76-80. (in

Chinese)

[7] 金光炎. 矩、概率权重矩与线性矩的关系分析[J]. 水文, 2005,

25(5): 1-6.

JING Guangyan. Analysis of relationship between moment,

probability-weighted moment and L-moment. Hydrology, 2005,

25(5): 1-6. (in Chinese)

[8] COHN, T. A., LANE, W. L. An algorithm for computing mo-

ments-based flood quantile estimates when historical flood in-

260

王俊珍，等：考虑历史洪水资料的 EMA 参数估计方法

第1卷 · 第4期

formation is available. Water Resources Research, 1997, 33(9):

2089-2096.

[9] 宋德敦. 不连序系列统计参数计算的新方法——概率权重矩

法[J]. 水利学报, 1989, 9: 25-32.

SONG Dedun. New method for calculating parameter estimation

with discrete series—Probability-weighted moment. Journal of

Hydraulic Engineering, 1989, 9: 25-32. (in Chinese)

[10] ENGLAND, J. F. Jr., SALAS, J. D. Comparisons of two mo-

ments-based estimators that utilize historical and paleoflood data

for the log Pearson type III distribution. Water Resources Re-

search, 2003, 39(9): 1243-1259.