Pure Mathematics
Vol.05 No.02(2015), Article ID:14956,4
pages
10.12677/PM.2015.52012
New Theorem for the Distributive Lattices
Youxue Xu
Zhanjiang TV University, Zhanjiang Guangdong
Email: 529568449@qq.com
Received: Mar. 5th, 2015; accepted: Mar. 14th, 2015; published: Mar. 19th, 2015
Copyright © 2015 by author and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
This paper discusses the operational properties of generated ideals and generated dual ideals. Then an example is given to point out that the conclusion of a proposition on P10 reference [1] is wrong. Two equivalent conditions for the distributive lattices are given.
Keywords:Distributive Lattice, Generated Ideal, Generated Dual Ideal
分配格的新定理
徐幼学
湛江广播电视大学,广东 湛江
Email: 529568449@qq.com
收稿日期:2015年3月5日;录用日期:2015年3月14日;发布日期:2015年3月19日

摘 要
首先讨论了格的子集生成幻和生成对偶幻的运算性质。然后给出一个反例,指出[1] 中一定理有误,并由此获得分配格的两个等价条件。
关键词 :分配格,生成幻,生成对偶幻

1. 生成幻及生成对偶幻的运算性质
本文用 表示集合的并(交),用
表示集合的并(交),用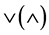 表示格中元的并(交)。
表示格中元的并(交)。
定义1:若格L的子集X满足下述性质:
若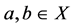 ,则
,则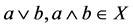
则X对于原来的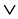 、
、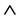 运算构成一个格,称之为L的子格,特别地,子格J闭于下时,即若
运算构成一个格,称之为L的子格,特别地,子格J闭于下时,即若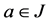 ,则
,则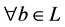 ,有
,有 时,称为L的幻,幻的对偶叫作对偶幻(即闭于上的子格)。
时,称为L的幻,幻的对偶叫作对偶幻(即闭于上的子格)。
定义2:格L的子集X的生成幻和生成对偶幻分别定义为L的包含X的最小幻和最小对偶幻,并分别用 和
和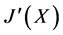 表示。
表示。
设X,Y是格L的子集,记
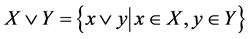
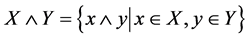
命题1:设L是格,X和Y是L的非空子集,那么
(1)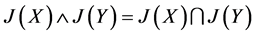 是幻。
是幻。
(2)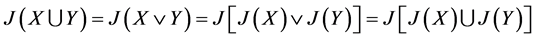 。
。
(3)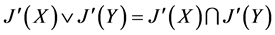 是对偶幻。
是对偶幻。
(4)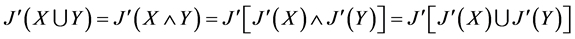 。
。
证:仅证(3)、(4)两式,(1)、(2)是(3)、(4)的对偶
(3) 设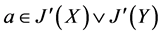 ,有
,有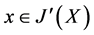 ,
, ,使
,使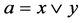 ,由于
,由于 ,
,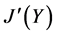 闭于上知,
闭于上知, ,
,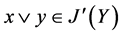 ,故
,故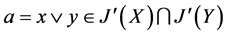 ,
,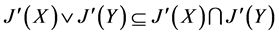 。
。
反之,设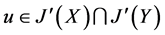 ,则
,则 ,
,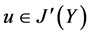 ,从而
,从而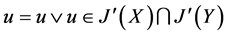 ,
,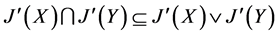 。
。
往证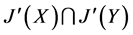 是对偶幻,设
是对偶幻,设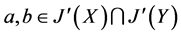 则
则 ,
, 。由
。由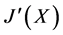 ,
,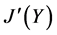 是子格易知
是子格易知 ,
,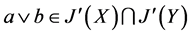 ,故
,故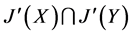 是子格。又设
是子格。又设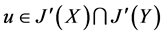 ,
,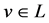 ,由
,由 ,
,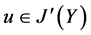 及
及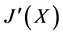 ,
, 闭于上知,
闭于上知,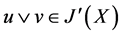 ,
,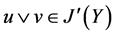 ,从而
,从而 ,故
,故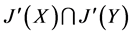 是对偶幻。
是对偶幻。
(4) 我们只要证:
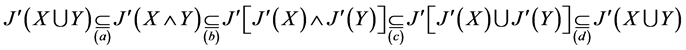
(a) 设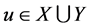 ,则
,则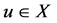 或
或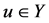 ,不妨设
,不妨设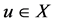 ,则对任意
,则对任意 ,有
,有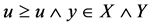 。
。
由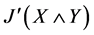 闭于上知,
闭于上知, ,从而
,从而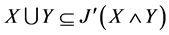 ,
,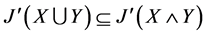 。
。
(b) 显然。
(c) 设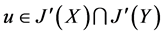 ,则有
,则有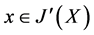 ,
,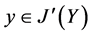 ,使
,使 ,
,
故

(d) 设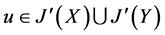 ,有
,有 ,或
,或 ,
,
故

证毕。
命题2:设L是格,X,Y是L的非空子集,则:
(1)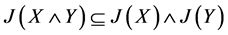 。
。
(2)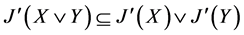 。
。
且上述包含关系均可不取等号。
证:(1)显然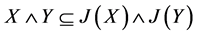 ,由命题1知
,由命题1知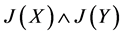 是幻,故
是幻,故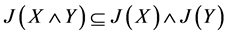 。
。
(2)是(1)的对偶。
例1:设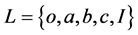 为菱形格,如图1,令
为菱形格,如图1,令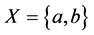 ,
,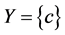 则
则
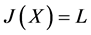 ,
,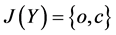
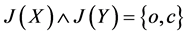
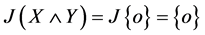
故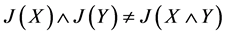 。
。
对偶地 。
。
命题3:设L是含有o,I的格,X,Y是L的非空子集,则
(1) 。
。
(2)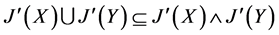 。
。
且上述包含关系均可不取等号。
证:(1) 设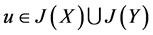 ,不妨设
,不妨设 ,因
,因 ,故
,故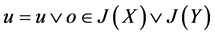 。
。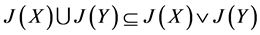 。
。
(2)是(1)的对偶。
例2:设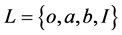 是四元格,如图2,令
是四元格,如图2,令 ,
,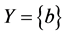 ,则
,则
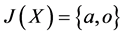 ,
,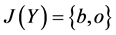
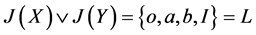
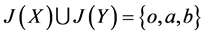
故 。
。
对偶地, 。
。
2. 分配格的两个等价条件
[1] 中P10指出:在格L中,由它的子集X,Y生成的幻的并(交),易知是由 ,
, 所作
所作 全体生成的幻*。
全体生成的幻*。
注*:由X生成的幻以J(X)表之,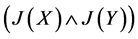
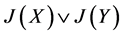 乃是L的含(含于)J(X)及J(Y)的最小(最大)幻,易证:
乃是L的含(含于)J(X)及J(Y)的最小(最大)幻,易证:
(1)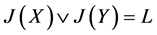 的含
的含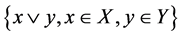 的最小幻。
的最小幻。
(2)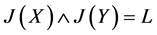 的含
的含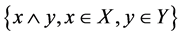 的最小幻。
的最小幻。
我们指出:[1] 中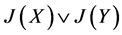 就是本文中的
就是本文中的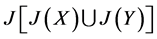 ,而(1)式右边=
,而(1)式右边=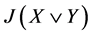 ,命题1已证得(1)式成立。而[1] 中的
,命题1已证得(1)式成立。而[1] 中的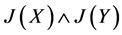 就是本文中的
就是本文中的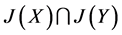 ,由命题1知
,由命题1知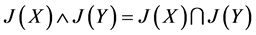 ,因此[1] 中的
,因此[1] 中的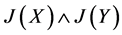 和本文定义的
和本文定义的 是一致的,但(2)式右边
是一致的,但(2)式右边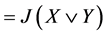 ,于是(2)式为
,于是(2)式为

Figure 1. Diamond lattice
图1. L菱形格

Figure 2. Four elements of lattice
图2. L四元格
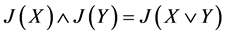
这与例1是矛盾的。
我们注意到例1是一个非分配格的例子,对于分配格,我们有如下定理:
定理:格L是分配格的充要条件是
(3) 
或
(4) 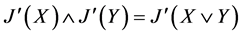
其中X,Y是格L的任意非空子集。
证:仅证(3)式,(4)是(3)的对偶。
必要性,设L是分配格,我们只要证
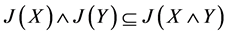
由命题1知,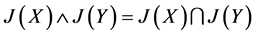 。设
。设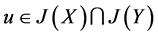 ,则
,则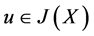 ,
,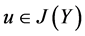 。从而存在
。从而存在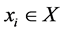 ,
,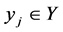 ,
,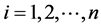 ;
;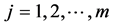 。使
。使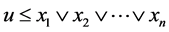 ,
, ,于是
,于是

由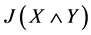 闭于下知,
闭于下知, ,
,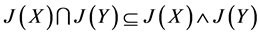 ,即
,即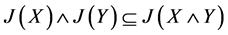 。
。
充分性,设在格L内(3)式恒成立,往证L是分配格,即对任意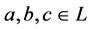 ,要证
,要证
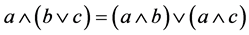
令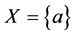 ,
,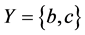 ,则
,则
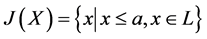

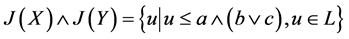
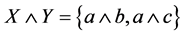
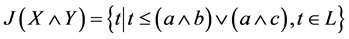
比较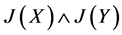 与
与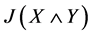 中最大元得
中最大元得
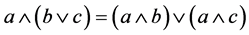
证毕。
基金项目
湛江市科技计划项目(编号:2013A01003)。
文章引用
徐幼学, (2015) 分配格的新定理
New Theorem for the Distributive Lattices. 理论数学,02,80-84. doi: 10.12677/PM.2015.52012
参考文献 (References)
- 1. 中山 正 (1964) 格论. 董克诚译. 上海科学技术出版社, 上海.