Pure Mathematics
Vol.05 No.05(2015), Article ID:16094,5 pages
10.12677/PM.2015.55033
Properties of the Solution of the Nonlinear Difference Equation

Wei Feng1, Yuchen Feng2
1School of Mathematics and Systems Science, Beihang University, Beijing
2Beijing No. 4 High School, Beijing
Email: wfeng_323@buaa.edu.cn, karlfeng1997@163.com
Received: Sep. 5th, 2015; accepted: Sep. 22nd, 2015; published: Sep. 25th, 2015
Copyright © 2015 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
In this paper, we obtain one sufficient condition of the boundedness of equation , and discuss the
convergence of the solution of equation and the sufficient and necessary condition
of existence of the periodic point with period 2 of the equation.
, and discuss the
convergence of the solution of equation and the sufficient and necessary condition
of existence of the periodic point with period 2 of the equation.
Keywords:Difference Equation, Nonlinear, Boundedness, Convergence

非线性差分方程 解的性态
解的性态
冯伟1,冯宇辰2
1北京航空航天大学数学与系统科学学院,北京
2北京四中,北京
Email: wfeng_323@buaa.edu.cn, karlfeng1997@163.com
收稿日期:2015年9月5日;录用日期:2015年9月22日;发布日期:2015年9月25日

摘 要
本文给出了差分方程 解的有界性的一个充分性条件,同时探讨了解了收敛性及二周期点存在的充分必要条件。
解的有界性的一个充分性条件,同时探讨了解了收敛性及二周期点存在的充分必要条件。
关键词 :差分方程,非线性,有界性,收敛性

1. 引言
阶数 的非线性差分方程:
的非线性差分方程:
 (1)
(1)
的全局行为在过去的几十年中备受人们关注。一般对此方程的研究前提是F和初始值集合 给定。到目前为止该领域的理论研究仍处在未成熟阶段,大多数成果是在F为有理式的情况下获得的。目前已获理论成果,详见文献[1]
,国内李先义和朱德明在差分方程领域给出了一些很好的结果[2] 。
给定。到目前为止该领域的理论研究仍处在未成熟阶段,大多数成果是在F为有理式的情况下获得的。目前已获理论成果,详见文献[1]
,国内李先义和朱德明在差分方程领域给出了一些很好的结果[2] 。
本文研究非线性差分方程:
 (2)
(2)
其初值为 ,并且
,并且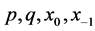 均为正值,
均为正值, 。
。
对于一般的差分方程(1),若F是连续可导函数,我们可以得出其线性化方程:
 (3)
(3)
这里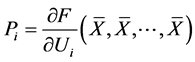 ,
,
 是方程(1)的平衡点。
是方程(1)的平衡点。
一般可通过线性化方程(3)的特征方程 的特征根的情况来判断该平衡点的稳定性[3] 。但方程(2)的线性化方程:
的特征根的情况来判断该平衡点的稳定性[3] 。但方程(2)的线性化方程:

的特征方程:
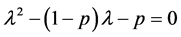
的特征根为1与 ,因此不能通过该方法判断该平衡点的稳定性。
,因此不能通过该方法判断该平衡点的稳定性。
由文献[4] [5] ,我们做变换 ,将方程(2)转化线性差分方程
,将方程(2)转化线性差分方程
 (4)
(4)
我们通过研究(4)来获得方程(2)的性质。
2. 主要结论
定理1:方程(2)存在二周期点的充分必要条件为 。
。
证明:
必要性:假定方程有一个二周期点,则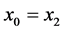 ,可得方程
,可得方程 ,变形得
,变形得 。
。
充分性:因为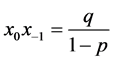 ,所以:
,所以:


同理可得 ,
, 。故
。故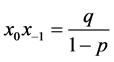 是方程有二周期点的充分必要条件。证毕。
是方程有二周期点的充分必要条件。证毕。
定理2:当 时,方程(4)的解全局收敛于其平衡点
时,方程(4)的解全局收敛于其平衡点 ,且当其初值
,且当其初值 大于
大于 时,其解单调递减收敛于
时,其解单调递减收敛于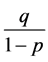 ,当其初值
,当其初值 小于
小于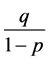 时,其解单调递增收敛于
时,其解单调递增收敛于 。
。
证明:
假定方程(4)有一个平衡点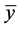 ,则
,则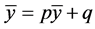 ,
求解得
,
求解得 。
。
由(4)得,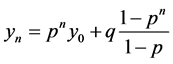 。
当
。
当 ,
, 。
。
因为: 。
。
所以,当 时,
时,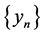 相邻两项之差恒大于0,方程(4)的解单调递增。又因方程(4)的
相邻两项之差恒大于0,方程(4)的解单调递增。又因方程(4)的
 趋向于
趋向于
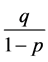 ,所以
,所以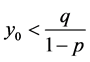 时方程(4)的解单调递增收敛于
时方程(4)的解单调递增收敛于 。
。
同理可得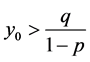 时,方程(4)的解单调递减收敛于
时,方程(4)的解单调递减收敛于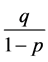 。证毕。
。证毕。
定理3:当 时,如果初值
时,如果初值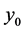 大于
大于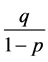 ,方程(2)的解构成的数列
,方程(2)的解构成的数列 ,
,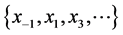 是单减数列,如果初值
是单减数列,如果初值 小于
小于 ,
, ,
, 是单增数列。
是单增数列。
证明:
当 时,
时, 单增,
单增, 。又因
。又因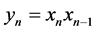 ,故
,故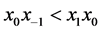 ,
, ,
,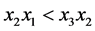 ,
, ,
,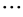 ,
, 。划去各个不等式两边相同的项,可得
。划去各个不等式两边相同的项,可得 ,
, 。所以
。所以 和
和 是单增数列。
是单增数列。
同理可得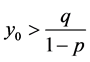 时,
时, 和
和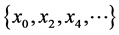 是单减数列。证毕。
是单减数列。证毕。
定理4:方程(2)的解构成的数列 有界等价于
有界等价于 有界。
有界。
证明:
设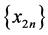 有界,由定理3,知
有界,由定理3,知 单调,故
单调,故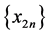 收敛于实数
收敛于实数 。当
。当 单增时,
单增时,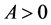 。又因为
。又因为 ,所以
,所以 收敛于
收敛于 ,所以
,所以 有界。当
有界。当 单减时,由定理3知
单减时,由定理3知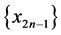 单减。由方程(2)的结构,如果初值非负,显然方程(2)的解是一个正数列。所以
单减。由方程(2)的结构,如果初值非负,显然方程(2)的解是一个正数列。所以 有界。
有界。
同理可证如果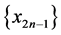 有界,则
有界,则 有界。证毕。
有界。证毕。
定理5: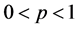 时,(2)的解有界。
时,(2)的解有界。
证明:
由定理3, 与
与 有相同的单调性。
有相同的单调性。
当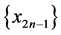 与
与 都单减时,又由于它们都是正数列,故有界。
都单减时,又由于它们都是正数列,故有界。
当 与
与 都单增时,如果它们之一无界,由定理4,则另一个也无界,故
都单增时,如果它们之一无界,由定理4,则另一个也无界,故 ,即方程(4)的解
,即方程(4)的解 也无界。由定理2
也无界。由定理2
这不可能,故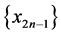 与
与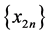 有界。
有界。
注1:从定理3和定理5知道,方程(2)的解形成的数列 与
与 收敛。进一步,这两个数列收敛的极限的乘积趋近于常数
收敛。进一步,这两个数列收敛的极限的乘积趋近于常数 ,这个常数是方程(2)任意两个二周期点的乘积。换言之,结合定理1知,方程(2)的任何解或者是一个二周期点,或者收敛于一个二周期点。
,这个常数是方程(2)任意两个二周期点的乘积。换言之,结合定理1知,方程(2)的任何解或者是一个二周期点,或者收敛于一个二周期点。
定理6. 对于 ,方程(2)的解
,方程(2)的解 构成的二维序列
构成的二维序列 收敛于双曲线
收敛于双曲线 正的一支。
正的一支。
证明:在平面直角坐标系下,做点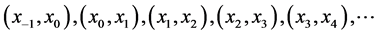 。
。
由定理2得方程(4)的解一定收敛于 。又因
。又因 ,所以方程(2)的解中相邻两项之积必定收敛于
,所以方程(2)的解中相邻两项之积必定收敛于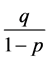 ,即最后得出的点
,即最后得出的点 必定收敛于双曲线
必定收敛于双曲线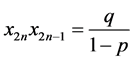 。又
。又 是正数列,故必收敛于位于第一象限那一支,参见图1,图2。证毕。
是正数列,故必收敛于位于第一象限那一支,参见图1,图2。证毕。
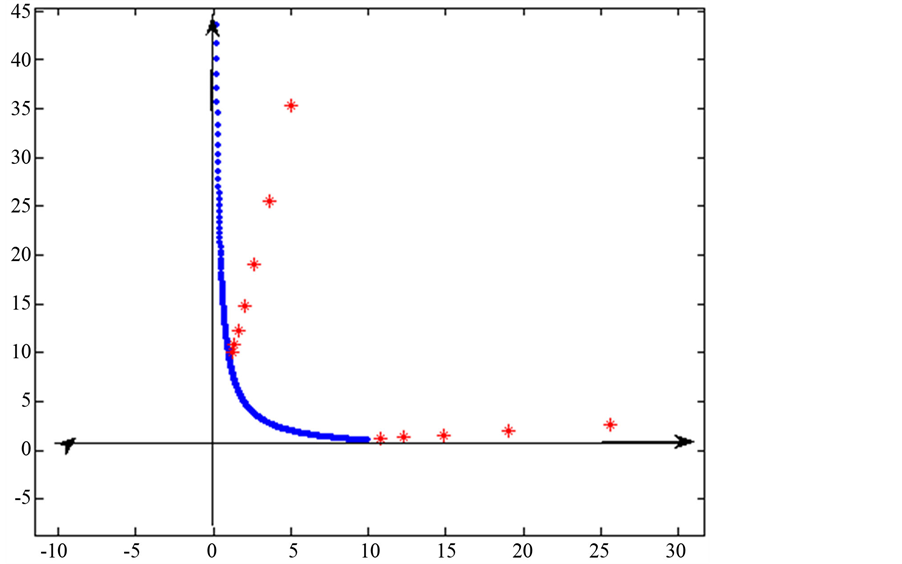
Figure 1. Convergence in the hyperbolic from above
图1. 从双曲线上方收敛于双曲线

Figure 2. Convergence in the hyperbolic from below
图2. 从双曲线下方收敛于双曲线
注2:虽然方程(2)的解是有界的,但不是一致有界的,这由定理3及一致有界的定义容易给出,故略去细节。
基金项目
本项目由中央高校基本科研业务费专项资金资助。
文章引用
冯 伟,冯宇辰. 非线性差分方程Xn=qx-1n-1+pxn-2解的性态
Properties of the Solution of the Nonlinear Difference Equation Xn=qx-1n1+pxn-2[J].
理论数学, 2015, 05(05): 233-237. http://dx.doi.org/10.12677/PM.2015.55033
参考文献 (References)
- 1. Kocic, V.L. and Ladas, G. (1993) Global behavior of nonlinear difference equations of higher order with applications. Kluwer Academic Publishers, Norwell. http://dx.doi.org/10.1007/978-94-017-1703-8
- 2. Li, X.Y. and Zhu, D.M. (2003) Two rational recursive sequences. Journal of Difference Equations and Applications, 9, 833-839.
- 3. Wang, J.L., Cai, H.T. and Feng, W. (2009) Dynamics of the difference equation . Journal of Shanxi University (Natural Science Edition), 32, 1-4
- 4. Stevic, S. (2011) On the difference equation . Applied Mathematics and Computation, 218, 4507-4513. http://dx.doi.org/10.1016/j.amc.2011.10.032
- 5. Duan, L.Y., Lun, D. and Deng, S.G. (2013) On boundedness of the nonlinear difference equation . Pure Mathematics, 3, 254-256. http://dx.doi.org/10.12677/PM.2013.34039