Pure Mathematics
Vol.06 No.01(2016), Article ID:16854,9
pages
10.12677/PM.2016.61009
Exploration on the Nature of Solutions for a Differential Equation of Fractional Order
Shiyou Lin1, Jie Ren2
1School of Mathematics and Statistics, Hainan Normal University, Haikou Hainan
2Li’an Junior High School, Lingshui Hainan

Received: Dec. 30th, 2015; accepted: Jan. 24th, 2016; published: Jan. 29th, 2016
Copyright © 2016 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
We prove existence and uniqueness of the solution of a nonlinear differential equation of fractional order. The differential operator is the Caputo fractional derivative. For the solvability of the equation is equivalent to a class of Volterra integral equation, we study the existence and uniqueness of the integral equation. We prove the existence of the solution of integral equation by Schau- der fixed point theorem and the uniqueness of the solution by contraction mapping principle.
Keywords:Differential Equation of Fractional Order, Caputo Derivative, Schauder Fixed Point Theorem, Contraction Mapping Principle

一类分数阶微分方程解的性质探讨
林诗游1,任洁2
1海南师范大学数学与统计学院,海南 海口
2黎安初级中学,海南 陵水

收稿日期:2015年12月30日;录用日期:2016年1月24日;发布日期:2016年1月29日

摘 要
本文主要证明了一类分数阶非线性微分方程解的存在性和唯一性。文中用到的微分算子是Caputo分数阶微分算子。因这类方程的可解性是与一类Volterra型的积分方程的可解性等价,所以我们主要研究了与之等价的积分方程解的存在性和唯一性。我们通过Schauder不动点定理证明了积分方程解的存在性,用压缩映象原理证明了解的唯一性。
关键词 :分数阶微分方程,Caputo微分,Schauder不动点定理,压缩映象原理

1. 背景介绍
尽管分数阶微积分的概念几乎是与整数阶微积分同时出现的,但在过去很长时间内,由于缺乏实际应用背景的促进而发展缓慢。直至近年,由于在物理,化学,生物等领域的广泛应用(参看[1] -[4] ),分数阶微分方程已成为数学领域中值得深入研究的重要方程之一。许多学者(参看 [5] - [8] )都研究过分数阶微分方程的性质,并取得了可观的收获。例如,Delbosco和Rodino [7] 以及El-Sayed [8] 证明了下面这个非线性分数阶微分方程的解的存在性和唯一性定理:

这里的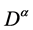 是黎曼–刘维尔分数阶微分。
是黎曼–刘维尔分数阶微分。
Diethelm和Ford [6] 深入研究过下面的分数阶微分方程:
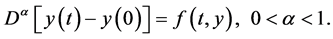
同样的,这里的 表示黎曼–刘维尔分数阶微分。
表示黎曼–刘维尔分数阶微分。
Kosmatov [9] 进一步证明了
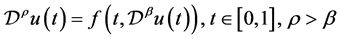
这里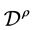 是指Caputo分数阶微分算子(参看 [10] ),这也是本文所用到的微分算子。
是指Caputo分数阶微分算子(参看 [10] ),这也是本文所用到的微分算子。
本文主要讨论的是一个分数阶非线性微分方程解的存在性和唯一性,研究方法主要是首先证明这个方程的可解性是与一个Volterra型的积分方程的可解性等价。文中用到的主要定理和Caputo微分算子的运算规则将在第2部分给出。第3部分和第4部分是关于方程的解的存在性和唯一性。
2. 预备知识和记号
首先给出本文用到的一个主要定理:
定理2.1. (Schauder不动点定理)设X是赋范线性空间,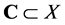 是非空的有界闭凸集。映射
是非空的有界闭凸集。映射 是连续的紧映射,那么
是连续的紧映射,那么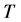 在
在 中有一个不动点。
中有一个不动点。
设函数 。如果
。如果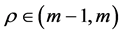 ,这里
,这里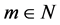 ,那么
,那么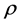 阶的Caputo分数阶微分定义为
阶的Caputo分数阶微分定义为
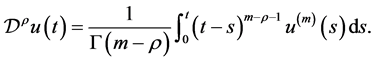 (2.1)
(2.1)
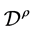 的逆算子定义为
的逆算子定义为
 (2.2)
(2.2)
本文的目的是考察非线性微分方程
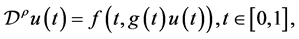 (2.3)
(2.3)
其中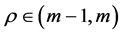 ,此方程满足初值条件
,此方程满足初值条件
 (2.4)
(2.4)
我们的目标为研究分数阶的问题,因此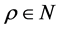 的情况不在我们的考虑范围内。
的情况不在我们的考虑范围内。
在下面的定理中,我们给出了(2.1)和(2.2)这两个算子的关系和它们的一些性质。
定理2.2. 设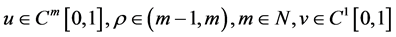 ,那么对于
,那么对于 ,成立
,成立
(a)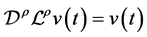 ;
;
(b)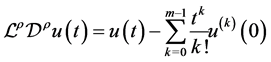 ;
;
(c)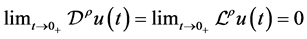 ;
;
(d) 如果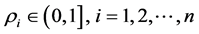 ,满足
,满足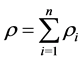 ,并且对于任一
,并且对于任一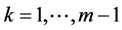 ,存在
,存在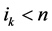 满足
满足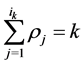 ,则下面的复合法则成立:
,则下面的复合法则成立:
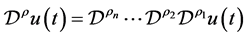 .
.
证明:(a) 令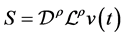 ,将(2.1),(2.2)代入
,将(2.1),(2.2)代入 中得
中得
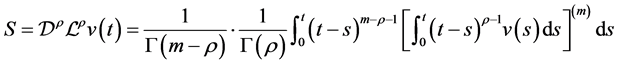
设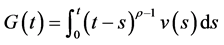 ,在上式中我们首先计算
,在上式中我们首先计算 。由
。由
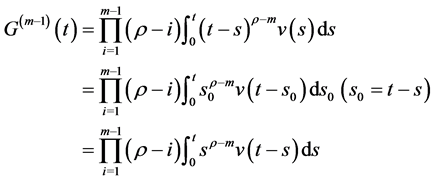
因此
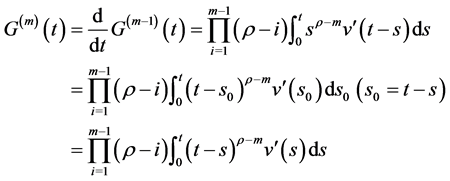
所以
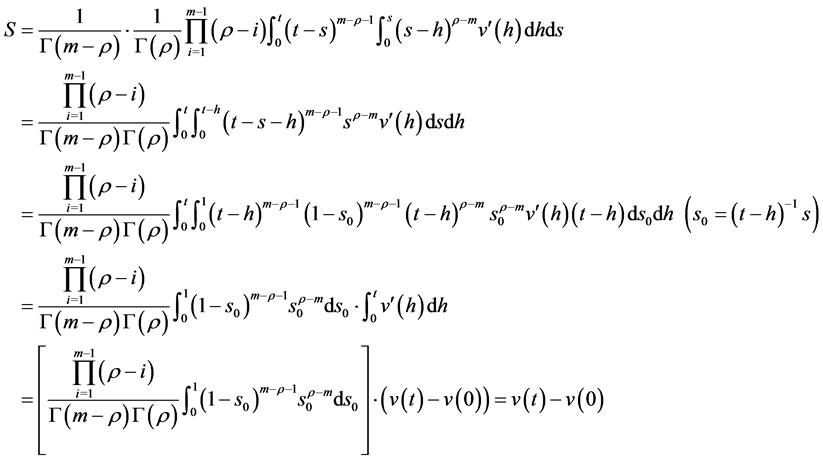
不妨设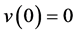 。则
。则 ,即
,即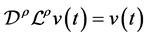 ,结论得证。(b),(c),(d)可类似证明,过程略。
,结论得证。(b),(c),(d)可类似证明,过程略。
分数阶微分的降阶可以通过以下定理实现,这也是下文将微分方程转化为积分方程时的主要技巧。
定理2.3. 设函数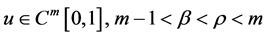 。那么对于所有的
。那么对于所有的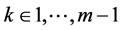 及任意
及任意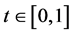 成立
成立
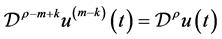 , (2.5)
, (2.5)
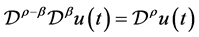 . (2.6)
. (2.6)
3. 解的存在性
这里我们主要为了在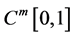 中找到初值问题(2.3)和(2.4)的解。
中找到初值问题(2.3)和(2.4)的解。
设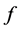 满足下面的条件:
满足下面的条件:
(H1)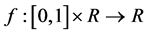 是连续可微函数;
是连续可微函数;
(H2) 存在非负函数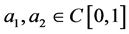 ,使得
,使得
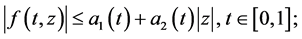
(H3)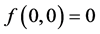 ,存在
,存在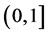 的一个紧子区间,使得
的一个紧子区间,使得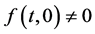 。
。
以下引理表明初值问题(2.3)和(2.4)解的存在性与Volterra型积分方程(3.2)解的存在性是等价的。
引理3.1.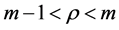 ,
, 满足(H1)和(H3)。函数
满足(H1)和(H3)。函数 是初值问题(2.3)和(2.4)的解的充要条件是
是初值问题(2.3)和(2.4)的解的充要条件是
 (3.1)
(3.1)
这里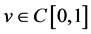 是下面这个积分方程的解
是下面这个积分方程的解
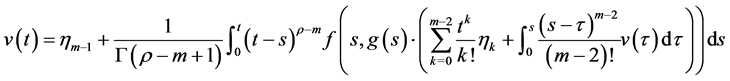 (3.2)
(3.2)
证明:(必要性)首先利用(2.5)式来对微分方程进行降阶。
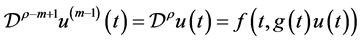
作代换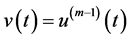 ,在等式两边同时作用算子
,在等式两边同时作用算子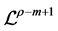 。由定理2.2(b)可得
。由定理2.2(b)可得
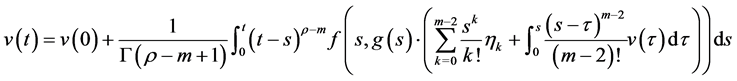
由于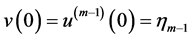 ,则上面的方程即为(3.2)。注意到
,则上面的方程即为(3.2)。注意到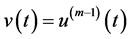 ,再应用积分公式即可得到(3.1)式。
,再应用积分公式即可得到(3.1)式。
(充分性)设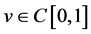 是(3.2)的一个解。因为
是(3.2)的一个解。因为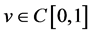 ,函数
,函数
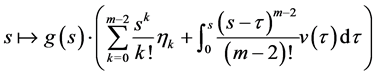
在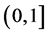 上连续,因此
上连续,因此

也在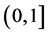 上连续。故
上连续。故 ,因此
,因此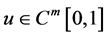 。而对(3.1)两边同求
。而对(3.1)两边同求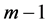 阶导,再考虑(3.2)可得
阶导,再考虑(3.2)可得
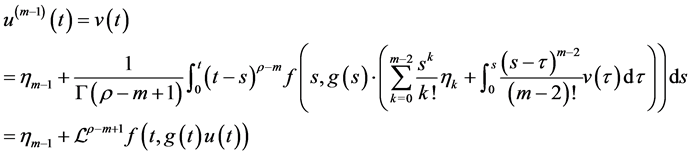
注意到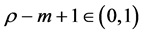 ,上边两式同时作用算子
,上边两式同时作用算子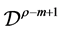 ,由定理(2.2)和(2.3)可得
,由定理(2.2)和(2.3)可得

因此我们证得了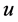 是(2.3)的解。又因为(3.2)式中的第二项在
是(2.3)的解。又因为(3.2)式中的第二项在 时趋于0,因此
时趋于0,因此 。故
。故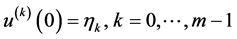 。
。
综上所述,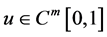 满足(2.3)和(2.4),充分性得证。
满足(2.3)和(2.4),充分性得证。
定理3.1. 设(H1),(H2),(H3)成立,如果下面两式成立:
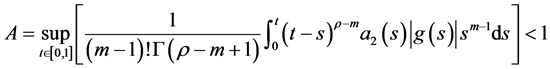 ,
,

那么积分方程(3.2)在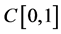 中有解。
中有解。
证明:在带有上确界范数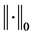 的赋范线性空间
的赋范线性空间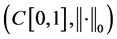 中,我们定义映射
中,我们定义映射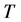 为
为

容易验证 有定义并且
有定义并且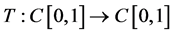 。
。
定义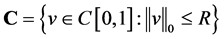 ,其中
,其中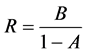 。则
。则 是
是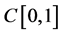 中有界闭凸集。
中有界闭凸集。
对于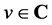 ,我们有
,我们有
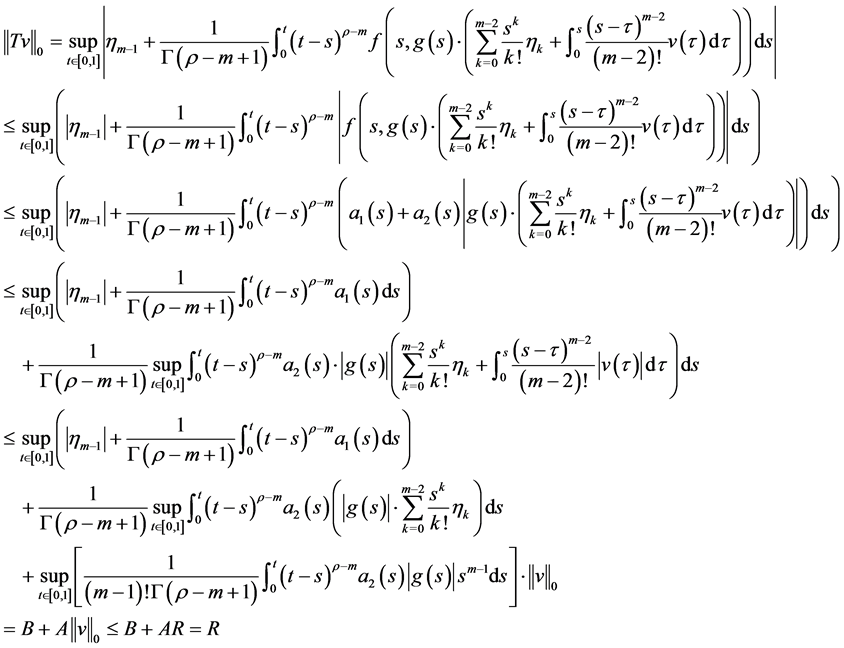
因此 ,即
,即 。另外容易验证映射
。另外容易验证映射 是连续的紧映射。
是连续的紧映射。
根据定理2.1,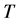 在
在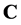 中有一个不动点,此即积分方程(3.2)的解,证毕。
中有一个不动点,此即积分方程(3.2)的解,证毕。
注:定理3.1中,要求 满足不等式
满足不等式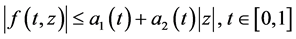 ,即要求
,即要求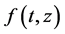 关于
关于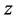 的增长不高于线性,这样满足解的存在性的方程就被限制在了一个很小的范围内。通过以下的定理我们将会看到,当
的增长不高于线性,这样满足解的存在性的方程就被限制在了一个很小的范围内。通过以下的定理我们将会看到,当 关于
关于 满足任意的多项式估计时,解的存在性仍然成立。
满足任意的多项式估计时,解的存在性仍然成立。
(H4) 存在非负函数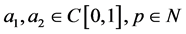 ,使得
,使得
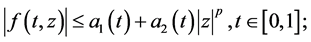
定理3.2. 设(H1),(H3),(H4)成立,定义

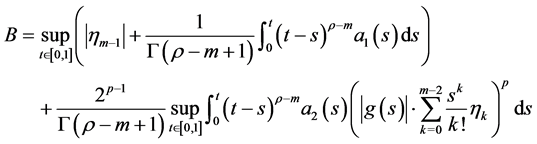
如果成立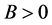 ,并且
,并且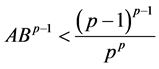 ,那么积分方程(3.2)在
,那么积分方程(3.2)在 中有解。
中有解。
证明:在带有上确界范数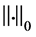 的赋范线性空间
的赋范线性空间 中,我们定义映射
中,我们定义映射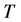 为
为
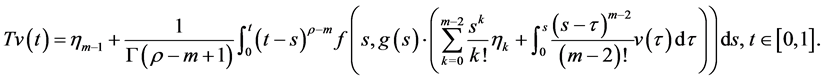
容易验证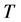 有定义并且
有定义并且 。
。
定义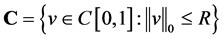 ,这里
,这里 待定。对于
待定。对于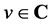 有
有
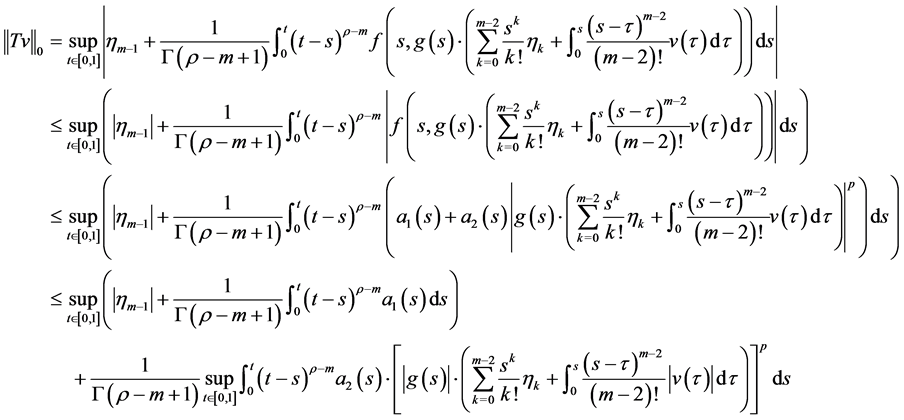
由幂平均不等式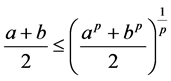 ,也即
,也即 。
。

类似定理3.1的证明,需要求得合适的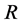 ,使得
,使得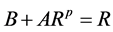 成立。
成立。
考查函数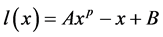 ,令
,令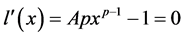 ,则
,则 ,由于
,由于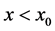 时
时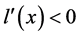 ;
;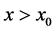 时
时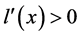 ,因此在
,因此在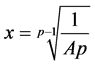 时取到最小值,只需要
时取到最小值,只需要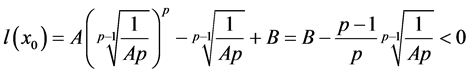 ,方程
,方程 就有正根,也即
就有正根,也即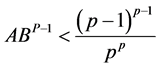 时存在
时存在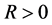 ,使得
,使得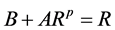 。因此
。因此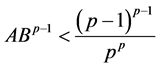 时,
时,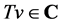 ,即
,即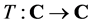 。
。
另外容易验证映射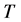 是连续的紧映射。根据定理2.1,
是连续的紧映射。根据定理2.1,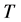 在
在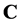 中有一个不动点,此即积分方程(3.2)的解,证毕。
中有一个不动点,此即积分方程(3.2)的解,证毕。
注:定理3.2成功地把定理3.1的结论推广到了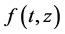 关于
关于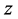 满足任意多次的多项式估计的情形。但是定理3.2中对于
满足任意多次的多项式估计的情形。但是定理3.2中对于 ,
,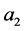 的限制比定理3.1严格,并且随着多项式次数
的限制比定理3.1严格,并且随着多项式次数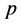 的提高,这个限制条件就越严格。因此在实际应用中,要根据具体情况选择这两个定理。
的提高,这个限制条件就越严格。因此在实际应用中,要根据具体情况选择这两个定理。
4. 解的唯一性
首先提出假设
(H5) 对于任意的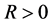 ,存在非负函数
,存在非负函数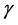 ,使得
,使得
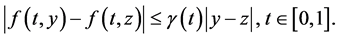
定理4.1. 如果(H1),(H3),(H5)成立,并且有
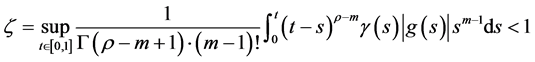 ,
,
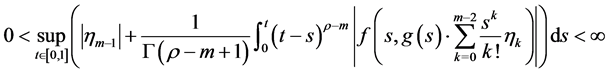 ,
,
那么积分方程(3.2)有唯一解。
证明:在Banach空间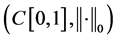 中,我们定义
中,我们定义 为
为
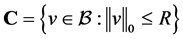
其中半径

定义映射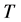 为
为
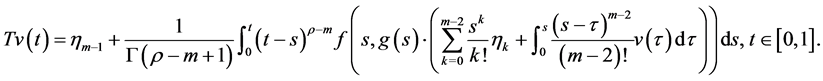
容易验证 有定义并且
有定义并且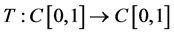 。
。
如果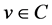 ,那么有
,那么有
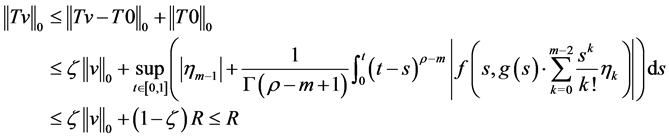
因此 是
是 到
到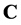 上的映射。
上的映射。
设 ,那么
,那么
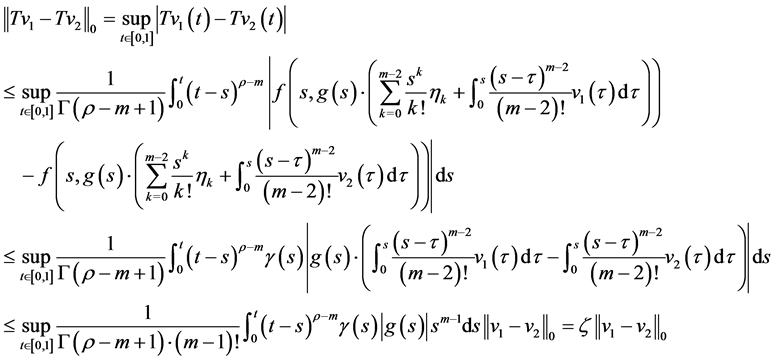
由于 ,因此
,因此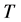 是一个压缩映射。根据压缩映像原理,
是一个压缩映射。根据压缩映像原理, 有唯一的不动点,此即积分方程(3.2)的解。
有唯一的不动点,此即积分方程(3.2)的解。
注:定理4.1在证明唯一性的时候用到了压缩映像原理,事实上同时能够得到解的存在性,因此原方程在满足条件(H5)时,解的存在性仍然成立。
致谢
感谢编辑和审稿专家对本文所付出的劳动,本文受到海南省自然科学基金(项目名称:Gronwall不等式的推广及其在微分方程中的应用;项目编号:20151011)的资助,在此一并表示感谢。
文章引用
林诗游,任 洁. 一类分数阶微分方程解的性质探讨
Exploration on the Nature of Solutions for a Differential Equation of Fractional Order[J]. 理论数学, 2016, 06(01): 56-64. http://dx.doi.org/10.12677/PM.2016.61009
参考文献 (References)
- 1. Miller, K.S. and Ross, B. (1993) An Introduction to the Fractional Calculus and Fractional Differential Equations. Wiley, New York.
- 2. Podlubny, I. (1999) Fractional Differential Equations. Academic Press, San Diego.
- 3. Samko, S.G., Kilbas, A.A. and Marichev, O.I. (1993) Fractional Integrals and Derivatives: Theory and Applications, Gordon and Breach. Gordon and Breach Science Publishers, Yverdon.
- 4. West, B.J., Bologna, M. and Grigolini, P. (2003) Physics of Fractal Operators. Springer, New York. http://dx.doi.org/10.1007/978-0-387-21746-8
- 5. Daftardar-Gejji, V. and Babakhani, A. (2004) Analysis of a System of Fractional Differential Equations. Journal of Mathematical Analysis and Applications, 293, 511-522. http://dx.doi.org/10.1016/j.jmaa.2004.01.013
- 6. Diethelm, K. and Ford, N.J. (2002) Analysis of Fractional Differential Equations. Journal of Mathematical Analysis and Applications, 265, 229-248. http://dx.doi.org/10.1006/jmaa.2000.7194
- 7. Delbosco, D. and Rodino, L. (1996) Existence and Uniqueness for a Nonlinear Fractional Differential Equation. Journal of Mathematical Analysis and Applications, 204, 609-625. http://dx.doi.org/10.1006/jmaa.1996.0456
- 8. El-Sayed, A.M.A. (1988) Fractional Differential Equations. Kyungpook Math. J, 28, 22-28.
- 9. Kosmatov, N. (2009) Integral Equations and Initial Value Problems for Nonlinear Differential Equations of Fractional Order. Nonlinear Analysis: Theory, Methods & Applications, 70, 2521-2529. http://dx.doi.org/10.1016/j.na.2008.03.037
- 10. Caputo, M. (1967) Linear Models of Dissipation Whose Q Is Almost Frequency Independent (Part II). Geophysical Journal International, 13, 529-539. http://dx.doi.org/10.1111/j.1365-246X.1967.tb02303.x