Pure Mathematics
Vol.07 No.04(2017), Article ID:21298,6
pages
10.12677/PM.2017.74035
Definition of Envelope in Differential Equations and a Problem that Must Be Noticed When Seeking Singular Solution
Zhihong Kong
Department of Mathematics, Taiyuan Normal University, Jinzhong Shanxi

Received: Jun. 18th, 2017; accepted: Jul. 3rd, 2017; published: Jul. 10th, 2017

ABSTRACT
In this paper, we explain that why the definition of envelope in differential equations is different from differential geometry, and give examples to illustrate. In addition, we illustrate a problem that must be noticed when seeking singular solution.
Keywords:Envelope, Tangent, Singular Solution, Supplement Function Value
微分方程中包络的定义及求奇解时必须注意的一个问题
孔志宏
太原师范学院数学系,山西 晋中
收稿日期:2017年6月18日;录用日期:2017年7月3日;发布日期:2017年7月10日

摘 要
说明了微分方程中给包络下的定义为什么与微分几何中包络的定义有所不同,并举例进行了分析,同时举例说明了求微分方程奇解时必须注意的一个问题。
关键词 :包络,相切,奇解,补充定义函数值

Copyright © 2017 by author and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 包络的定义问题
微分方程通解曲线族的包络的定义 [1] 设给定单参数曲线族
 , (1)
, (1)
其中c是参数, 是x,y,c的连续可微函数。曲线族(1)的包络是指这样的曲线,它本身并不包含在曲线族(1)中,但过这曲线的每一点,都有曲线族(1)中的一条曲线和它在这点相切。
是x,y,c的连续可微函数。曲线族(1)的包络是指这样的曲线,它本身并不包含在曲线族(1)中,但过这曲线的每一点,都有曲线族(1)中的一条曲线和它在这点相切。
微分几何中曲线族的包络的定义 [2] 对于给定的平面曲线族Cλ: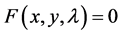 ,如果在这平面上存在曲线C,使得C与这族曲线中每一条曲线Cλ都相切,而且曲线C完全由这些切点组成,则平面曲线C称为这平面曲线族Cλ的包络。
,如果在这平面上存在曲线C,使得C与这族曲线中每一条曲线Cλ都相切,而且曲线C完全由这些切点组成,则平面曲线C称为这平面曲线族Cλ的包络。
从上面的两个定义可以看出,作为微分方程中曲线族的包络的曲线,要求的就是过它上面的每一点,都要有曲线族(1)中的一条曲线和它在这点相切。而作为微分几何中曲线族的包络的曲线,要求的是曲线族中的每一条曲线都要与它相切,同时,包络完全由这些切点组成。
我们说,作为微分方程中曲线族的包络,不能要求曲线族中的每一条曲线都要与它相切,否则,就无法建立微分方程(通解)曲线族的包络与奇解的等价关系,更无法利用求解通解曲线族的包络的方法确定微分方程的奇解了。因此,同为包络,由于在不同学科中的应用不完全相同,在具体的定义方面就产生了(也需要产生)一定的差异。
2. 举例说明
例1求微分方程
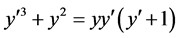 (2)
(2)
的奇解。
解方程(2)即为
 ,
,
 ,
,
 .
.
方程的通解为
 (3)
(3)
及
 , (4)
, (4)
还有一个特解为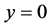 。
。
对积分曲线族(3)由于 ,所以(3)没有包络。对积分曲线族(4),
,所以(3)没有包络。对积分曲线族(4),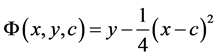 ,
,
 。c—判别式为
。c—判别式为

解得c—判别曲线为

由于 ,
,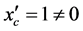 ,满足非蜕化条件,因此Γ是第二个积分曲线族(4)的包络,因而
,满足非蜕化条件,因此Γ是第二个积分曲线族(4)的包络,因而 是原方程的奇解。但是这里的
是原方程的奇解。但是这里的 不与积分曲线族(3) (其中
不与积分曲线族(3) (其中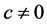 )中的曲线相切,也不相交。如果按照微分几何中包络的定义,
)中的曲线相切,也不相交。如果按照微分几何中包络的定义, 就不是方程通解曲线族的包络,也就得不到这个奇解了。
就不是方程通解曲线族的包络,也就得不到这个奇解了。
例2求微分方程
 (5)
(5)
的奇解。
解方程(5)即为
 ,
,
 .
.
方程的通解为
 (6)
(6)
及
 (7)
(7)
其中c1,c2为任意常数。不失一般性,可取 ,这样方程的通解可写为
,这样方程的通解可写为
 (8)
(8)
它的c—判别式为

解上面方程组,得到符合题意的一条c—判别曲线

对第一个积分曲线族
 ,
,
 ,
, .
.
满足非蜕化条件,因此Γ是第一个积分曲线族的包络, 是原方程的奇解。但是在积分曲线族(8)中,平行直线族
是原方程的奇解。但是在积分曲线族(8)中,平行直线族 与奇解
与奇解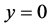 相交而不相切。如果按照微分几何中包络的定义,
相交而不相切。如果按照微分几何中包络的定义, 就不是曲线族(8)的包络,从而不能采用求包络的方法得到这个奇解了。
就不是曲线族(8)的包络,从而不能采用求包络的方法得到这个奇解了。
3. 求奇解时必须注意的一个问题
该问题通过举例加以说明。
例3判断方程
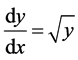 (9)
(9)
是否存在奇解,如果存在就求出来。
解右端函数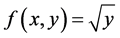 在
在 的上半平面定义、连续。
的上半平面定义、连续。

当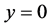 时无界,所以方程如果有奇解,只能是
时无界,所以方程如果有奇解,只能是 ,显然
,显然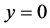 是方程的一个解,当
是方程的一个解,当 时可求得方程的通解为
时可求得方程的通解为
 ,
,
即
 , (10)
, (10)
其中 ,c是任意常数。现在求通解的包络,这里
,c是任意常数。现在求通解的包络,这里
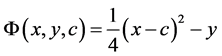 ,
,
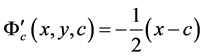 .
.
已知 是方程的解,而在通解中
是方程的解,而在通解中 时,
时, ,补充定义
,补充定义 。解方程组(c—判别式)
。解方程组(c—判别式)
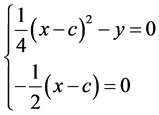
得c—判别曲线

由于 ,
, ,满足非蜕化条件,故c—判别曲线
,满足非蜕化条件,故c—判别曲线 为通解曲线族(10)的包络,从而为方程(9)的奇解。
为通解曲线族(10)的包络,从而为方程(9)的奇解。
注在求通解的过程中可知 !因此在c—判别式这个方程组中,x不能等于c!为此在解方程组求c—判别曲线之前必须补充定义函数值:
!因此在c—判别式这个方程组中,x不能等于c!为此在解方程组求c—判别曲线之前必须补充定义函数值: 时,
时,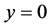 。否则
。否则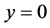 与积分曲线族(10) (其中,
与积分曲线族(10) (其中,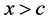 ,从而
,从而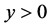 )没有公共点!谈何相切?
)没有公共点!谈何相切?
例4判断方程
 (11)
(11)
是否存在奇解,如果存在就求出来。
解右端函数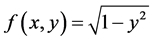 ,它在带形区域:
,它在带形区域: ,
, 上定义、连续。
上定义、连续。

当 时无界。所以方程如果有奇解,只能是
时无界。所以方程如果有奇解,只能是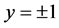 ,显然
,显然 是方程的两个解。当
是方程的两个解。当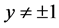 时可求得方程的通解为
时可求得方程的通解为
 ,
,
即
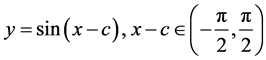 , (12)
, (12)
其中c是任意常数。现在求通解曲线族的包络,这里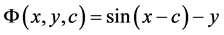 ,
,
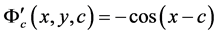 。已知
。已知 是方程的解,而在通解中当
是方程的解,而在通解中当 时
时 ,补充定义
,补充定义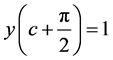 ;同理,补充定义
;同理,补充定义 ,解方程组(c—判别式)
,解方程组(c—判别式)

得两条c—判别曲线
 与
与
对这两条c—判别曲线,均有 ,
,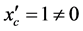 ,满足非蜕化条件。故两条c—判别曲线
,满足非蜕化条件。故两条c—判别曲线 与
与
 都是通解曲线族(12) (这时
都是通解曲线族(12) (这时 )的包络,从而是方程(11)的奇解。
)的包络,从而是方程(11)的奇解。
注与前面类似,通解是当 时得到的,这时
时得到的,这时 !同样,在解方程组求c—判别曲线之前必须补充定义函数值:当
!同样,在解方程组求c—判别曲线之前必须补充定义函数值:当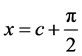 时
时 ;当
;当 时,
时, 。
。
当然,对于例3也可以这么解:当允许 (或
(或 )时,通解(10)就表示了方程所有的解,接下来可以直接解方程组求c—判别曲线,而不必定义函数值。同样,对于例4,也可以这样叙述:当允许
)时,通解(10)就表示了方程所有的解,接下来可以直接解方程组求c—判别曲线,而不必定义函数值。同样,对于例4,也可以这样叙述:当允许
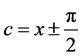 (或)时,通解(12),其中,就表示了方程所有的解,接下来可以直接
(或)时,通解(12),其中,就表示了方程所有的解,接下来可以直接
解方程组求c—判别曲线,而不必定义函数值。
文章引用
孔志宏. 微分方程中包络的定义及求奇解时必须注意的一个问题
Definition of Envelope in Differential Equations and a Problem that Must Be Noticed When Seeking Singular Solution[J]. 理论数学, 2017, 07(04): 271-276. http://dx.doi.org/10.12677/PM.2017.74035
参考文献 (References)
- 1. 王高雄, 周之铭, 朱思铭, 等. 常微分方程[M]. 第3版. 北京: 高等教育出版社, 2006: 103-104.
- 2. 沈纯理, 黄宣国. 微分几何[M]. 北京: 经济科学出版社, 1997: 46-47.