河北地质大学数理教学部,河北 石家庄
收稿日期:2024年2月25日;录用日期:2024年3月20日;发布日期:2024年3月27日

摘要
用符号Cn表示顶点集为X的n-边形。任意取定顶点
,用
表示关于点x的稳定子群(Cn的自同构群中的子群)的中心化子代数。在本文中,我们首先通过点x的稳定子群在集合
上的作用构造出
的一组基。然后,给出
的三个子代数使得它们的向量空间直和恰好是
。最后,我们证明代数
和代数T相等,这里
表示Cn的关于点x的Terwilliger代数。
关键词
n-边形,中心化子代数,Terwilliger代数

The Centralizer Algebra of the Ordinary n-Cycle
Wei Zhao
School of Mathematics and Science, Hebei GEO University, Shijiazhuang Hebei
Received: Feb. 25th, 2024; accepted: Mar. 20th, 2024; published: Mar. 27th, 2024

ABSTRACT
Let Cn denote the Ordinary n-cycle with vertex set X. Fix any vertex
, and let
denote the centralizer algebra of the stabilizer of x in the automorphism group of Cn. In this paper, we first give a basis of
by this stabilizer acting on
. Moreover, we give three subalgebras of
such that their direct sum is just
as vector space of matrices. Finally, we show that the two algebras
and T coincide, where
denotes the Terwilliger algebra of Cn with respect to x.
Keywords:Ordinary n-Cycle, Centralizer Algebra, Terwilliger Algebra

Copyright © 2024 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
设
为一距离正则图,其顶点集为Y,边集为E。取定顶点
,则图Γ关于顶点x的稳定子群(Γ的自同构群中的子群)的中心化子代数是由在点x的稳定子群作用下的全体不变矩阵所组成的矩阵集合,这里矩阵的行标与列标由集合Y中元素所标定。一般来说,图Γ的中心化子代数
的一组基可以通过关于点x的稳定子群作用在集合
上得到,但有时也可能是比较困难的。
Terwilliger代数(或次成分代数)对于距离正则图的研究十分重要,并且已成为代数组合理论的重要研究内容 [1] [2] [3] 。我们知道代数Terwilliger代数是中心化子代数的子代数。一个重要的研究问题是对于哪些距离正则图其中心化子代数和Terwilliger代数相等。事实上,对于某些距离正则图,其中心化子代数和Terwilliger代数已经被证明是相等的。例如,对于Hamming图,A. Schrijver等人刻画了该图的中心化子代数的一组基,并证明了其中心化子代数和Terwilliger代数相等 [4] [5] ;对于Johnson图,谭莹莹等人证明了其中心化子代数和Terwilliger代数相等 [6] ;对于折叠n-立方图,侯利航等人刻画了该图的中心化子代数的一组基,并证明了其中心化子代数和Terwilliger代数相等 [7] 。基于上述文献,本文研究了n-边形的中心化子代数结构:刻画了n-边形的中心化子代数的一组基,并证明了其中心化子代数和Terwilliger代数相等。本文所用的方法可以看做是上述文献 [7] 中研究方法的一种推广。
n-边形是一类经典的有Q-多项式结构的距离可迁图 [8] 。但其中心化子代数还没有被完全刻画。在本文中,我们将刻画n-边形的中心化子代数结构。为了讨论方便,用符号Cn来表示n-边形,其顶点集为
。任取两个不同的顶点
,它们邻接当且仅当
或
。由此可得图Cn的距离函数:
(1)
这里
为小于或等于a的最大整数。由(1)可知图Cn的直径为
。
在本文中,取定
并把该点作为图Cn的基点。设
是关于点x1的稳定子群(Cn的自同构群中的子群)的中心化子代数。我们首先给出了点x1的稳定子群作用在集合
的所有轨道,每个轨道只含有一个或两个元素。通过在每个轨道上定义相应的0-1矩阵,得到了
的一组基(见定理3.5)。然后,我们给出
的三个子代数并计算它们的维数(见命题3.6~3.8)。此外,这三个子代数的向量空间直和恰好是
(见引理3.9)。最后我们证明代数
和代数T相等并得到了T的一组基,这里
表示图Cn关于点x1的Terwilliger代数(见定理3.11和定理3.12)。
为了更好地理解本文,在本节的最后给出一些主要符号的说明:
:复数域。
Y:有限非空集合。
:复数域
上的全体
阶方阵构成的矩阵代数,其中矩阵的行标与列标Y的元素标定。
:有限无向的,没有环与重边的连通图,
分别为其顶点集和边集。
:点x在图
的自同构群中的稳定子群。
Cn:顶点集为X的n-边形,其中
。
:图Cn关于点x1的中心化子代数。
:图Cn关于点x1的Terwilliger代数。
2. 预备知识
在本节,我们将介绍有关距离正则图和中心化子代数的一些概念和基本事实。
设是
复数域,Y是一个非零有限集合。由域
上的全体
阶方阵构成的
-代数记为
,称为全矩阵代数,其中矩阵的行标与列标由Y的元素标定。
设
为一个有限无向的,没有环与重边的连通图。用
表示图Γ的距离函数。设
,称D为图Γ的直径。如果对于任意的整数
和任意顶点对
和
满足
,存在图Γ的自同构映射把x映到u,y映到v,那么称图Γ是距离可迁的。对于任意的
满足
,如果整数
与
的选
取无关,那么我们称图Γ是距离正则的。注意到距离可迁图一定是距离正则图,反之不一定成立。在本节以下部分,假设图Γ是一距离正则图。
取定
,并把点x作为基点。设
为点x在Γ的自同构群中的稳定子群。任取
,
。如果对任意的
,有
,则称矩阵M在
的作用下是不变的。由
作用下的全体不变矩阵所组成的矩阵集合称为
的中心化子代数(作为集合)。接下来,我们将介绍中心化子代数的一些子代数:Bose-Mesner代数,对偶Bose-Mesner代数以及Terwilliger代数。
对于每一个
,设矩阵
,其
-位置元素
,如果
;
,如果
。易知矩阵
张成了全矩阵代数
的一个交换子代数,我们称这个代数为图Γ的Bose-Mesner代数。事实上,Bose-Mesner代数可以由邻接矩阵A1生成。
取定
,并把点x作为基点。对于每一个 。设
为
中的对角矩阵,其
-位置元素
,如果
;
,如果
。易知矩阵
张成了全矩阵代数
的一个交换子代数,我们称这个代数为图Γ关于点x的对偶Bose-Mesner代数。
。设
为
中的对角矩阵,其
-位置元素
,如果
;
,如果
。易知矩阵
张成了全矩阵代数
的一个交换子代数,我们称这个代数为图Γ关于点x的对偶Bose-Mesner代数。
图Γ的Bose-Mesner代数和对偶Bose-Mesner代数生成全矩阵代数的一个子代数,我们称这个子代数为图Γ关于点x的Terwilliger代数(或次成分代数)。
关于距离正则图和Terwilliger代数的更多知识,可参考文献 [1] [2] [3] [8] 。
3. Cn的中心化子代数
回顾第一节中n-边形Cn的定义。本节给出图
的中心化子代数的一组具体的基。由于Cn是距离可迁图,因此可取定顶点
作为基点。用符号
表示点x1在Cn的自同构群中的稳定子群。易知稳定子群由集合X上的两个变换组成:
(2)
这里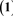 表示恒等变换:
;
表示集合X上的一个变换:
表示恒等变换:
;
表示集合X上的一个变换:
,
.
对于每一个有序2-元组
,定义相应的整数3-元组
如下:
(3)
注意到
。易知所有满足(3)的整数3-元组
构成如下集合
:
(4)
对于
中任意整数3-元组
,由(1),(3)可知,满足
的
可以分为如下四种情况:
(i) 如果
,则
。由(1)式可知,
。
(ii) 如果
,则
,
。由(1)可知,当
时,
;当
时,
。
(iii) 如果
,则
,
。由(1)可知,当
时,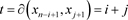 ;当
时,
。
;当
时,
。
(iv) 如果
,则
。由(1)可知,
。
根据上述四种情况,定义
的三个子集:
命题3.1 对于
,我们有
(5)
并且
的基数为
(6)
这里的
表示大于或等于a的最小整数。
证由集合
的定义易知,当n为奇数时
,即
。当n为偶数时,
。所以有(5)成立。接下来,我们计算集合
的基数。由
是两两互不相交的,所以有
(7)
通过计算可得
(8)
将(8)代入到(7)中得到(6)。
对于每一个
,定义如下集合:
(9)
接下来,对于每一个
,我们将给出集合
的意义。为此,我们先分别给出集合S1的一个子集:
(10)
和S3 (n为偶数时)的一个子集:
。
命题3.2 对于每一个
,以下(i)~(iii)成立。
(i) 对于
,我们有
(ia) 如果
,则
;当n为偶数时,
(ib) 如果
,则
(ii) 对于
,我们有
(iii) 对于
并且n为偶数,我们有
(iiia) 如果
,则
。
(iiib) 如果
,则
证根据集合
,
的定义,以及上述有关
的四种情况的讨论可得。
命题3.3 集合
,
是稳定子群
作用在集合
上的所有轨道。
证由定义可知
,
构成了集合
的一个分拆。任取
,
,设
,容易证明当映射
取遍稳定子群
时,
能够取遍集合
。事实上,任取
,
。由(2)可知,变换
为
,或者
为
。基于此事实可知,对于给定的
,稳定子群
可迁地作用在集合
上。
定义3.4对于每一个
,定义矩阵
如下:
注意到矩阵
的转置为
,并且矩阵
,
是线性无关的。由命题3.3可知,矩阵
在
的作用下是不变的。以矩阵
,
为一组基张成的域
上的线性空间记为
。事实上,
就是稳定子群
的中心化子代数。因此,
,
构成了代数
的一组基。
定理3.5集合
是代数
的一组基,其维数为
证由命题3.1和命题3.3可证。
接下来,我们将给出
的三个子代数,并计算它们的维数。为此,下面先给出
的三个子空间:以矩阵
,如果
,为一组基张成
的一个子空间,记为
;以矩阵
,如果
,为一组基张成
的一个子空间,记为
;以矩阵
,如果
,为一组基张成
的一个子空间,记为
。
命题3.6子空间
是
的子代数,其维数为
(11)
证易知
对矩阵加法,数乘,共轭转置和矩阵乘法封闭。因此
是
的子代数。为了计算
的维数,只需计算
的基数。定义
三个的子集如下:
易知
,
,
。所以有
(12)
通过计算得到
将上述结果代入(12)中得到(11)成立。
命题3.7子空间
是
的子代数,其维数为
(13)
证类似于命题3.6的证明,可知
是
的子代数且
为了计算
的基数,定义
两个子集如下:
由定义可知
通过计算得到
因此(13)成立。
命题3.8子空间
是
的子代数,其维数为
(14)
证类似于命题3.6的证明,可知
是
的子代数且
为了计算
的基数,定义
三个子集如下:
易知当
时,
,所以我们有
通过计算得到
因此(14)成立。
引理3.9我们有
(向量空间直和)。
证由定理3.5和命题3.6~3.8可知,
是
的子代数,并且
,从而该引理成立。
对于图Cn,用
和
分别表示它的第k个距离矩阵和第k个对偶幂等元,用
表示由
和
生成的Terwilliger代数。
引理3.10以下(i)~(iii)成立。
(i) 对于每一个
有
(15)
(ii) 任意
有
(16)
(ii) 对于每一个
有
(17)
证(i)当
时,考虑等式(15)两端矩阵的
-位置元素。容易验证当
时,
,否则
。
(ii) 在(15)式的等号两端左乘
,右乘
得到(16)。
(iii) 将
代入(16)可得(17)。
定理3.11 代数
。
证要证明两个代数相等,只需证明这两个代数互相包含即可。因为
,
是代数
的一组基,所有矩阵
生成了代数T。一方面,由引理3.10 (i) (iii)可知代数T的每一个元素都属于代数
,因此有
。另一方面,由引理3.10 (ii)可知代数
的每一个元素都属于代数T,因此有
。所以,代数
。
定理3.12集合
构成了代数T的一组基,其维数为
证由定理3.5和定理3.11得证。
接下来以5-边形C5为例来说明本文的方法和结论。
对于C5,顶点集为
。由公式(2)可知图C5顶点x1的稳定子群
。根据(4)有
由此可以得到稳定子群
作用在集合
上的轨道
由定理3.5可知,图C5的中心化子代数
的一组基为
其维数为
相应地,由命题3.6~3.8可知。
的一组基为
,其维数为
。
的一组基为
,其维数为
。
的一组基为
,其维数为
。
另一方面,图C5的所有距离矩阵为
。所有对偶幂等元为
。由引理3.10可知
并且
因此对于图C5有代数
,这里
表示图C5关于点x1的Terwilliger代数。
文章引用
赵 伟. n-边形的中心化子代数
The Centralizer Algebra of the Ordinary n-Cycle[J]. 理论数学, 2024, 14(03): 89-99. https://doi.org/10.12677/pm.2024.143088
参考文献
- 1. Terwilliger, P. (1992) The Subconstituent Algebra of an Association Scheme I. Journal of Algebraic Combinatorics, 1, 363-388. https://doi.org/10.1023/A:1022494701663
- 2. Terwilliger, P. (1993) The Subconstituent Algebra of an Association Scheme II. Journal of Algebraic Combinatorics, 2, 73-103.
- 3. Terwilliger, P. (1993) The Subconstituent Algebra of an Association Scheme III. Journal of Algebraic Combinatorics, 2, 177-210. https://doi.org/10.1023/A:1022415825656
- 4. Gijswijt, D., Schrijver, A. and Tanaka, H. (2006) New Upper Bounds for Nonbinary Codes. Journal of Combinatorial Theory, Series A, 13, 1719-1731. https://doi.org/10.1016/j.jcta.2006.03.010
- 5. Schrijver, A. (2005) New Code Upper Bounds from the Terwilliger Algebra and Semi definite Programming. IEEE Transactions on Information Theory, 51, 2859-2866. https://doi.org/10.1109/TIT.2005.851748
- 6. Tan, Y., Fan, Y., Ito, T. and Liang, X. (2019) The Terwilliger Algebra of the Johnson Scheme J (N,D) Revisited from the Viewpoint of Group Representations. European Journal of Combinatorics, 80, 157-171. https://doi.org/10.1016/j.ejc.2018.02.029
- 7. Hou, L., Hou, B., Kang, N. and Gao, S. (2022) The Terwilliger Algebra of the Halved N-Cube from the Viewpoint of Its Automorphism Group Action. European Journal of Combinatorics, 101, 103480. https://doi.org/10.1016/j.ejc.2021.103480
- 8. Brouwer, A.E., Cohen, A.M. and Neumaier, A. (1989) Distance-Regular Graphs. Spring, Berlin.https://doi.org/10.1007/978-3-642-74341-2






 。设
为
中的对角矩阵,其
-位置元素
,如果
;
,如果
。易知矩阵
张成了全矩阵代数
的一个交换子代数,我们称这个代数为图Γ关于点x的对偶Bose-Mesner代数。
。设
为
中的对角矩阵,其
-位置元素
,如果
;
,如果
。易知矩阵
张成了全矩阵代数
的一个交换子代数,我们称这个代数为图Γ关于点x的对偶Bose-Mesner代数。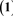 表示恒等变换:
;
表示集合X上的一个变换:
表示恒等变换:
;
表示集合X上的一个变换: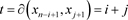 ;当
时,
。
;当
时,
。