Journal of Advances in Physical Chemistry
Vol.04 No.02(2015), Article ID:15363,17
pages
10.12677/JAPC.2015.42011
A Quantum Chemistry Study of Hydrogen Bonds (1)
Guangyao Zhou
Beijing Kein Research Center for Natural Sciences, Beijing
Email: 13923756124@163.com
Received: May 10th, 2015; accepted: May 25th, 2015; published: May 29th, 2015
Copyright © 2015 by author and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
In this paper, the coupled cluster CCSD and other quantum chemistry methods are employed to study various kinds of representative hydrogen bond systems, as well as lithium bond, sodium bond and halogen bond systems; the MO and Δρ are observed before and after the formation of hydrogen bonds. We believe that these bonds have the common underlying mechanism, and a new concept about H-bond is needed to be established. The new concept of H-bond can be described as follows: When orbital symmetries are properly matched, the intramolecular or intermolecular electrons at high-energy level (HOMO) will partially transfer to lower energy regions (LUMO) and forms electron-shared, energy-reduced, relatively stable electrostatically interacting system. Quan- tum chemistry calculations faithfully described this phenomenon and fact. With practical calculation examples, the basic character of the electron transfer and the specific details of the new concept of H-bond are introduced.
Keywords:Quantum Chemistry, Hydrogen Bond, Electronegativity Equalization Principle, New Concept of H-Bond
氢键的量子化学研究(一)
周光耀
北京科音自然科学研究中心,北京
Email: 13923756124@163.com
收稿日期:2015年5月10日;录用日期:2015年5月25日;发布日期:2015年5月29日

摘 要
本文通过耦合簇CCSD等量子化学方法,对各种类型氢键选择有代表性分子进行了计算,还包括锂键、钠键和卤键,观察了形成氢键前后的MO和Δρ,认为它们有着共同的机制、本质,需要建立新的氢键概念。氢键新概念总的可表述为:氢键是分子内、分子间处于能级较高部位的电子(HOMO),在轨道对称性相符时,向能级较低部位(LUMO)偏移部分电子,形成了双方共享电子能量降低的较稳定静电作用体系。量子化学计算描述了这种现象和事实。用计算实例介绍了这种电子偏移的基本情况和氢键新概念具体细节。
关键词 :量子化学,氢键,电负性均衡原理,氢键新概念

1. 一些基本概念
量子化学的一些基本概念,多是从数理出发提出的。这里则是一个从事实验化学的人,在作量子化学应用时的直观想象,这想象是企图符合量子化学计算所描述的化学客观存在的,是从理化出发的。进一步的想象要结合后面具体的例子才能细说。
本工作用GAMESS-US程序[1] 进行量子化学计算,方法和基组统一用CCSD/6-311++G**。实践表明,该计算精确地计算了电子相关,能够正确地计算通常的成键、氢键和范德华作用。能量、优化构型采用CCSD计算的结果,而MO则采用SCF density计算的结果,以便对MO方便作图。
进一步用Multiwfn 3.1 [2] 进行数据处理。作图则用VMD [3] 等。
距离不标出单位时是Å,电荷和能量数值不标出单位时是a.u.,频率不标出单位是cm−1。
1.1. 关于量子化学计算
量子化学计算,是在对于一个给定的原子核空间排布(单点计算),如何在核之间安排电子使体系能量最低。或者为了使体系电子能量最低还要挪动原子核(优化计算)。
DFT (Density Functional Theory)就是在算电子密度,认为通过体系电子密度可得到体系一切性质。
MO (Molecular Orbital)理论,虽然在计算化学体系的电子波函数(y,MO),而波函数可通过y2 = r得到电子密度r,得到电子在原子核之间的密度分布,并选定能量最低时r对应的波函数,也是在原子核空间排布中安排电子。同样可以说,通过化学体系的MO可以得到体系一切性质。反过来说,没有一种性质是脱离MO的表达而存在的。
正是这个在核之间安排电子,决定了体系的能量。现在电子分布计算日益合理、精确,已经具有实际意义,体系电子分布和能量同样是反映客观化学存在的。
然而,对于电子密度r,即使作图来看,它也只是一个浓厚的囫囵云团,不易看明白,于是发展了许多将电子密度进行拓扑运算,如AIM理论,从中发现电子密度分布的规律性,成功地用来研究氢键存在的各种特征。本文则只用MO提供的原生态信息,企图认识氢键的形成过程和本质。
在MO理论,它将各个MO按能量、轨道对称性安排,以对应分子中各个原子核之间的各种联系:成键、反键、非键,σ、π、n (孤对电子)、δ等各种对称性电子。MO包含了分子的全部化学性质。特别是对于小分子,MO与σ、π、n各种对称性电子可以恰好对应,有利于进行图形分析。
本文以代表性的小分子从各MO并配合电子密度差Δρ来研究氢键,看形成氢键的前后相应的MO发生了什么变化,从而解读氢键形成的机制和本质。
当然,对于较大的分子,从MO并不那么容易看明白,但是MO所表明的氢键形成的机制和本质还是同样存在的。
1.2. 关于电负性均衡原理
在DFT, Parr等人[4] 指出:电负性是体系电子化学势的负值。
同样应该有:在MO理论,电负性χ是原子AO能级或分子MO能级ε的负值。
能级ε是从轨道上拿走一个电子所要付出的能量,电负性χ则是该轨道吸引电子的能力。这是一个客观事实的两个相反的观察视角,用一个负号表达视角的相反。电负性视角接近化学实践习惯,是人们感知的一种客观存在。
不同电负性的原子组成分子时,原子参加成键的轨道(以基组表示),通过得失部分电子调整着电子对核的屏蔽,从而调整着自己的电负性,也即调整着自己的能级。
在原子之间成键时,电负性大的原子参加成键的轨道得到部分电子,电子对核的屏蔽增强,使其电负性降低,电负性小的原子失去部分电子,电子对核屏蔽减弱,其电负性升高,从而达到双方电负性均衡、不再有电子流动。
这是电负性均衡原理企图概括的事实,它是能量最低原理的一种表现形式。水往低处流,直至均衡。
然而Sanderson电负性均衡原理[5] 认为,初始电负性不同的多个原子化合成分子时,它们的电负性会发生平均化,各原子实际所具有的电负性,为所有原子电负性的几何平均,即分子中所有原子的电负性都是相等的。
实际上,这仅是一种经验猜测。只有双原子分子和几个特定的小分子才是这样,对广大的分子这种认为分子中所有原子的电负性都是相等的并不成立。
我在进行基团电负性计算时,曾经得出结论[6] :
“电负性均衡原理应该完整地表述为:在基态分子中,任一个键两边参与成键的基团(包含只有一个原子的基团)的键轨道实际所具有的电负性是相等的;电负性均衡并不是指分子中每个原子的电负性都趋向均衡,它们的电负性虽然有变化,但一般仍是不相等的。”
现在进一步提出:
在分子的一个MO中,各个原子的电负性是相等的、均衡的,它的值就是这MO的电负性(能级的负值)。这是在MO理论中电负性均衡原理的基本表述。
当然,这还逻辑地包含一些更为具体的内容:
所说的分子中原子的实有电负性,是指原子参与组成该MO (基组线性组合)的电负性。
分子的各种轨道,包括σ、π、n、δ等各层轨道,都各自实现着电负性均衡,包含简并轨道。
但这是否又回到了“分子中所有原子的电负性都是相等的”?也不是。因为由于轨道对称性不同,一个MO常常并不会包含分子的所有原子,仅只是部分原子,还有许多原子在另外的MO,在那里实现均衡。不同MO中的同种原子电负性也是不同的。
可以想见,当将一个分子某一部位的键断开,像切三明治样断开多层MO,由于每个MO都是电负性均衡的,这断开键的两边电负性也是相等的。
形成共价键的双方、形成氢键的双方、形成范德华作用的双方,也是通过转移部分电子实现了双方电负性均衡的。
虽然说通过转移电子实现了MO的电负性均衡,MO上的电子有均衡的能级,但是由此而来分子的电荷分布则并不均衡,电负性相对小的原子如H,它的核在端头部位很裸露,相对电负性大的原子如O、F电荷聚集太多,从而形成了分子的电荷分布不均匀,形成极性。
1.3. 关于静电作用
在前文[7] 曾经说过,静电作用的正、负电荷以及它们的相互作用,是人类较早的实验、理论研究课题。它的基本规律是同性电荷互相排斥,异性电荷互相吸引,可以定量地用库仑定律表达:

在化学领域,涉及到微观的原子、电子,同样是静电作用的世界,核是正电荷,电子是负电荷,同样是同性排斥、异性吸引。
在量子化学,基础是Schrödinger 方程,为此要构造Hamilton能量算符。算符中包含了核、电子的全部静电作用。在构造的Hamilton算符中可以看到:
ZaZbe2/rab,是核与核的排斥;
−Zae2/ria,是核与电子的吸引;
e2/ rij,是电子与电子的排斥。
经典力学的物理量与量子力学的算符之间就是这样地对应一致。
只是,在量子化学中,电子不再仅是一个质点,它同时是波,它无处不在,它是一片云,只能用统计的方法来描述、把握。现在,核吸引的是电子云,电子之间的排斥也是电子云之间的。
还有,在氢键、范德华作用范畴,电子相关对计算至关重要,因为它对电子排布的疏密有影响。
实际上氢键、范德华作用也只是静电作用的一种具体表现形式和结果。氢键、范德华作用中,都是体系之间的电子与电子、核与核之间的斥力,与共享电子的引力的平衡,这些都是静电作用。对此不妨称之为(广义)静电作用。
分子间氢键的静电作用,不能仅经典地想象成分子间两团正负电荷相互摄动、吸引而不会改变自己,既然是正负电荷在相互吸引,这正负电荷的聚集形态会发生变化,从而使体系发生变化。
具体到氢键双方,有两种情况:如果双方轨道对称性相符、不正交,由于静电作用,一方处于能级高位的电子(HOMO)要向另一方处于能级低位的轨道空域(LUMO)转移、偏移电子。如果双方轨道正交,那双方只能相互摄动、吸引,也会引起双方各自变形,但不直接在其间发生电子的转移、偏移。对这种情况才不妨称之为狭义静电作用。
图1是(HF)2静电势(ESP)的xy截面图,用几何级数来生成等值线,等值线起始值为±0.01,步长为2,生成正负各10条线。
图1的上部是两个自由HF的ESP图并列放在一起,两个图是一样的,只是方位采用的是氢键二聚体中的,以便与下面氢键图比较。
对一个自由HF,从ESP线推知的电子聚集看,HF除了在键间聚集了电子外,由于电负性差距,H还向F转移了许多电子,电子对F核屏蔽增强,F对其上的孤对电子吸引力减弱,孤对电子能级显著升高,孤对电子变得蓬松,它构成了ESP的负值区域(虚线),这里电子能级高,电子易于给出。ESP的正值值区域(实线)紧裹在HF键的周围,这里是能级低的势阱,易于接受电子。
由此可以想象,当两个HF相接近,HF-1的孤对电子会向HF-2的正值空域偏移电子,形成图1的下部(HF)2氢键ESP。这里,由于HF-1孤对电子向HF-2的势阱偏移,电子能级降低,HF-1孤对电子的蓬松消融了,二者之间形成了统一的氢键正值线区。HF-2孤对电子还在,更加蓬松了一点。

Figure 1. ESP of (HF)2
图1. (HF)2的ESP
在静电作用中举一个这样的例子,是着重强调氢键不能仅看作是两团正负电荷相互摄动、吸引而不会改变自己的狭义静电作用,即象图1上部HF-1和HF-2那样,虽然它指明了氢键是怎样形成的,但还要考虑氢键形成带来的变化。在双方轨道对称性相符、不正交的情况下,电子要从高能级流向低能级的空域,电子发生偏移,这决定了氢键的构型和基本性质,有共价性。而在这种电子偏移氢键生成的架构之下,双方另外轨道在对称性不相符、正交的情况下,仍存在正负电荷相互摄动、吸引而不那么改变自己的狭义静电作用,即离子性的内容。
双方在形成氢键时常是有多种选择的,比如(HF)2,如果仅认为静电作用是两团正负电荷相互摄动、吸引,那么它应是直线型的,因为F的外端电子过多,而另外分子的H端电子缺失裸露,且不正好?但实测和计算都是F的孤对电子与对方形成氢键,而孤对电子并没有过多的电子,没有负电荷,它只是能级被抬得很高而已,以致孤对电子偏移部分电子到低能势阱时能量下降,这才是主调。不仅是正负电荷的狭义静电吸引。
静电驱动下的电子偏移形成了一种氢键的基本架构、锚定。在这框架下存在着所有形式的静电作用:电子与电子的排斥、核与核的排斥,核对电子的吸引,不同的核共同吸引其间的电子。MO只是在这种静电格局下电子的分布和能级。
实际上,静电驱动下的电子偏移形成氢键,远比总体的ESP复杂,本文将进一步从体系的MO来考察、分析轨道相互作用。
1.4. 关于氢键形成的轨道相互作用
量子化学应用的直观想象,在氢键体系,怎样看待一个MO以及MO的之间的相互作用呢?轨道为什么会相互作用呢?
选一个简单的例子也许更易说明一些,如ClH⋯·CH3 [8] 这样的单电子氢键。它只有一个MO与形成的氢键对应,见图2。
图2分为三列:
左列是ClH (分子1)的氢键相关MO。1MO10即LUMO (等值面取0.021),对应ClHσ*,其后是轨道能级值。下面1MO7 (等值面0.02,默认值,以后不再标示),对应ClHσ键。
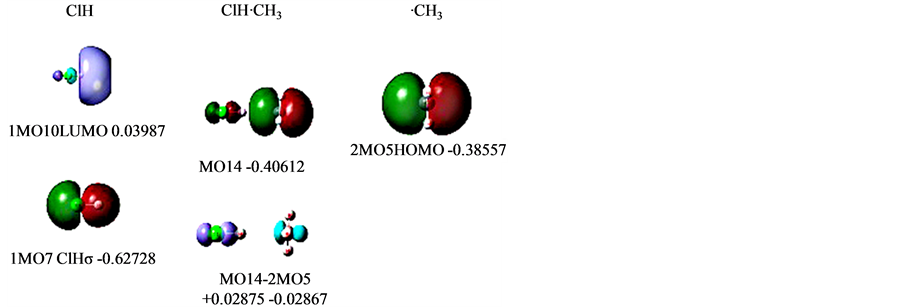
Figure 2. MOs of ClH-CH3
图2. ClH-CH3的MOs
其它为内层电子和孤对电子,它们都不直接参与形成氢键,“照搬”到氢键体系中,没有列出。
右列是甲基·CH3(分子2)。2MO5是其单电子HOMO,正是它要形成氢键。内层电子和CHσ键,都照搬到氢键体系中,没有列出。
中列是氢键分子ClH⋯·CH3。MO14是它的HOMO,是2MO5向1MO10偏移电子形成的。内层电子、孤对电子和CHσ键都照搬到氢键体系中,没有列出。
本工作没有像通常那样将各轨道按能级的高低排位,而是将轨道的前后演变关系基本放在一个水平上,以便能够看清轨道的这种演变。
和通常分析此类问题一样,先会观察给出电子方·CH3的HOMO与接受电子方ClH的LUMO。
初看,二者的这两个能级相差巨大,LUMO能级甚高。而量子化学计算表明二者生成氢键时,是没有能垒、自发能量降低的。且氢键的形成并不改变双方分子原有的价键结构。
说量子化学计算是在核之间安排电子(用电子密度ρ表示),当然也是说在安排电子状态波函数(MO,基组的线性组合表示)。这就是说在一定部署的核势场中,如果安排电子,电子需要处于这样的状态波函数MO,具有对应的电子密度分布ρ。如ClHσ键1MO7就是这状态的形象。
然而进一步还要问,对于ClHσ键,这样一个核外已布居了电子的整体,它又形成什么样的势场呢?形成什么样的势阱呢?也即在其上额外再布居电子会取什么样的状态函数和密度分布呢?
ClHσ键1MO7,是由Cl的P型和H的S型轨道以相位相符组成的SP杂化成键轨道。它周围空域形成的势阱必定具有和它有相应的特征,其实ClH的LUMO即1MO10,就是在ClHσ键外围空域再额外布居一个电子时的电子状态。Cl还是P型,H还是S型,只是这时双方是反相位、反键的分离对峙,反映了在ClH的σ键外围空域再额外布居电子是要拉开这个键的,它能级很高,是正值。
从LUMO的定义看,它是一个能量最低的空轨道。既是空轨道哪来能量、能级?其实是设想当另有一个电子加入到该分子时,这个电子所处的最低能级。这可以通过计算来验证:计算得到HCl的LUMO能级为0.03987。如果多加一个电子即计算HCl−,这时这个单电子的能级为0.03521。
这时,由于是2MO5向1MO10偏移生成了MO14,可以作MO14与2MO5的电子密度差来求得偏移电子量(1MO10为空),图2中列之下就是这个密度差图。ClHσ*上增加了电子0.02875,电负性下降,能级上升至−0.40612。而·CH3的P型轨道失去电子0.02867,电负性上升,能级下降至−0.40612,从而达到了氢键两边的电负性均衡。
但如果这时不是增加一个电子,而是微量电子,ClHσ键外围这个空域的“能级”会有多高呢?可以想象,如果增加的电子是无穷小量,这“能级”就会在ClHσ键的外围空域,逐渐增加电子量,电子之间排斥加大,则能级逐渐升高,直至加到一个电子能级成为LUMO,ClHσ*。
不妨具体推算一下。通常认为一个原子、基团、分子片,它的电负性随着其上电子少量增减呈线性变化[6] ,即χ* = (1 + q)χ,χ是原子或基团原有的电负性,χ*是在其上增减了电子量q后的电负性。
如·CH3的2MO5,电负性是能级的负值即0.38557,这是χ。它在生成氢键时失去了0.02867电子,这样用上面的公式计算,得到χ*为0.3967 (相应的能级再加负号),这与氢键轨道MO14符合。失去电子电负性增大了。
再算一下HCl的LUMO当没有电子在其上时的起始点。χ*就是MO14的能级负值0.4061,这是得到电子量为0.02875后的结果,在公式中取q为负值,反推它的起始电负性为0.4181,也即HCl的LUMO在没有电子时的起始能级为−0.4181。
在图2右列,甲基·CH3,2MO5是它的单电子,HOMO,它是一个P型轨道,正是它要受ClHσ键在外围空域所形成的势阱的吸引,电子要向ClH*偏移,部分电子要落于这个势阱之中。额外的电子进入ClHσ键外围空域,它将采取ClHσ键在外围空域所形成的势阱LUMO大致形象,至于所处的“能级”高低则取决于进入外围空域ClHσ*的电子量。由于空域ClHσ*是反键、反相位的,MO14中偏移电子与它的母体也还是反相位的。
这里,展示了氢键所谓轨道相互作用、混合的原因和数量。
从图2左边看,势阱LUMO形象是Cl的 P型和H的S型反相位对峙。当·CH3的P型轨道整体平移过去时,与对方H的空位S型势阱正交,(这与双方都有电子时,P型的一端与S型相位相符的组合成键不一样),偏移的部分电子要落于这个势阱对称性相符的Cl上。MO14的形象正是这样,H上没有偏移电子,偏移电子落在Cl上。
当然MO14所展现的电子偏移能级下降并不是唯一的变化,由于·CH3移走了电子,电子排斥减小,氢键中·CH3的各个MO的能级都有所下降。反之因ClH接受了电子,电子排斥增大,氢键中ClH的各个MO的能级都有所上升。
要综合地看总体的能量变化,但电子偏移架构下形成的电子共享却是总体能量下降的主体、本源。
计算的氢键结合能为:0,002738(7.277 kJ/mol)。双方相距(H⋯C)2.47717。
偏移电子落入了ClHσ键外围的反键空域ClHσ*。这使得ClHσ键由自由状态到氢键中,键长由1.27903微伸长至1.27907。
这里,分析是比较氢键生成前后的MO变化过程,并用电子密度差来确定HOMO向LUMO的电荷偏移转移量,这样准确、简单明了。
2. 氢键的新概念
2.1. 历来氢键种类[9]
1) 通常经典的氢键
这是氢键的最初发现和研究时的种类,表示为X-H…Y,其中X 和Y一般都是电负性较大的元素,像N、O、F、Cl等,且Y具有孤对电子。
其代表分子如:(HF)2、(H2O)2
2) 非经典的氢键体系
这是随着对氢键的不断研究,氢键的范围不断扩大形成的,比如:
X H⋯Y型(X=C,N;Y = F, N, O, S, Cl, Br )
π型氢键:FH⋯CH2=CH2,FH⋯苯
双氢键 如:LiH⋯HF,HBeH⋯HF
单电子氢键 如:FH⋯·CH3
3) 类氢键体系:
本工作还将一些没有H的体系,认为与氢键有共同的机制,也包括进来,称为类氢键,如:锂键、鈉键、卤键。
2.2. 氢键新概念基本表述
长期以来,在化学界关于氢键的本质存在许多争议,如静电作用说与共价说,什么是氢键作用力的本质?氢键的概念必须是根植于氢键的本质的。
本工作对各类型有代表性分子的氢键进行了量子化学计算,观察形成氢键前后的MO和Δρ,认为它们有着共同的机制、本质,需要归纳出新的概念。
氢键新概念总地可以表述为:氢键是分子内、分子间处于能级较高部位的电子(如HOMO),在轨道对称性相符、不正交时,向能级较低部位(如LUMO)的势阱偏移了部分电子,形成了双方共享电子、能量降低的较稳定的静电作用体系。量子化学计算描述了这种现象和事实。
这里,说能级较高部位的电子向能级较低部位偏移部分电子,把锂键、鈉键、卤键等都包含了。但由于历史的缘故,还是统称为氢键,广义的氢键。
甲方的HOMO电子向乙方的LUMO偏移部分电子,实际上是甲方的HOMO电子要进入乙方势力范畴,要服从乙方核所形成的势场或势阱,也即LUMO。这种HOMO电子偏移进了乙方,它平衡了双方的电负性,拉拢了甲乙双方,形成了双方更大范围的电子共享。也即为什么仅仅是很小的电荷转移,也会产生很大的能量贡献。
将Levine的Quantum chemistry第五版476页的图复制为图3,它是根据Feynman力的公式计算得出的。引用同核双原子的图作为参照,因为氢键通过电子偏移双方电负性已经是相等的了。
此图清楚地看到成键(现在是氢键)时双方之间存在着的成键区,即共享电子区。而正是甲方的HOMO些许电子向乙方的LUMO偏移、锚定,构成了这种共享电子格局。图2的MO14正是这样,电子偏移锚定了共享电子空间。ClH端头裸露的H,虽然没有接受偏移电子,但它对延伸过来的P型单电子的狭义静电吸引还是存在的,H同时吸引双方的经典氢键形象是存在的,它是氢键的内容之一。
2.2.1. 以 FH⋯·CH3为例
FH⋯·CH3 [8] 也为单电子氢键,见图4。
图4左列是FH (分子1)。上面是它的LUMO(等值面0.04),是FHσ*,记为1MO6,随后是轨道能级值。下面是1MO3,对应FHσ键。其它内层电子和孤对电子没有列出,它们都不直接参与形成氢键,照搬到氢键体系中。
右列是甲基·CH3 (分子2)。2MO5是其单电子HOMO,它要向FHσ*偏移电子形成氢键。内层电子和CHσ键没有列出,都照搬到氢键体系中。
中列是氢键分子FH⋯·CH3。MO10是它的氢键MO。下面是MO10的Δρ,其下是正、负电荷量。内层电子、孤对电子和CHσ,没有列出。
先观察给出电子方·CH3的HOMO与接受电子方FH的LUMO。
对于FHσ键1MO3这样状态的形象,它表明在这样的核势场中,安排电子,电子需要处于这样的状态波函数,具有对应的电子密度分布。
然而对于FHσ键,这样一个核外已经布居了电子的整体,它此外又形成什么样的势场、势阱呢?也即在其上额外再布居电子会取什么样的状态函数和密度分布呢?
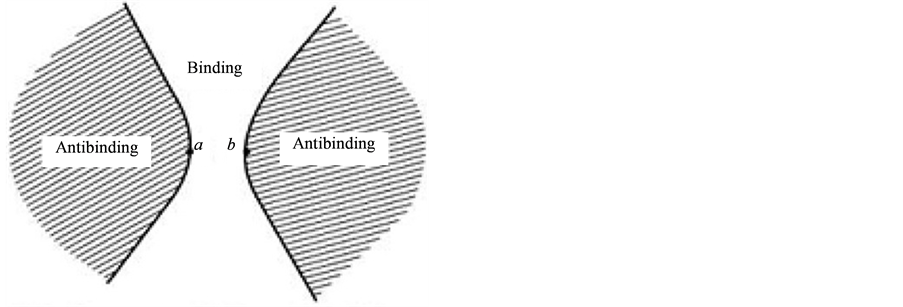
Figure 3. Cross section of binding and antibinding regions
图3. 成键区和反键区的截面
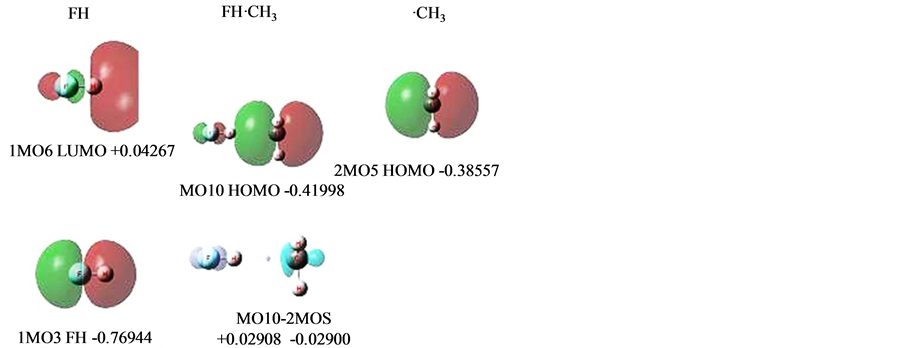
Figure 4. MOs of FH-CH3
图4. FH-CH3的MOs
FHσ键1MO3,是由F的P型和H的S型轨道以相位相符组成的成键轨道。它周围空域形成的势阱必定具有和它有相应的特征,其实FH的LUMO FHσ*即1MO6,就是在FHσ键外围空域再额外布居一个电子时的状态。F还是P型和H还是S型,只是这时双方是反相位、反键分离对峙的,反映了在FH的σ键外围空域再额外布居电子要拉开这个键,能级很高,是正值。
从LUMO的定义看,它是一个能量最低的空轨道。既是空轨道哪来能量、能级?其实是设想当另有一个电子加入到该分子时,这个电子所处的最低能级,也可以是分子自身电子激发到这个能级。这也可以通过计算来验证:计算得到HF的LUMO能级为0.04285。如果多加一个电子即计算HF-,当HF不弛豫-,这时这个单电子的能级为0.04067。
这时,由于是2MO5偏移生成了MO10,可以作MO10与2MO5的电子密度差来求得偏移电子量。FHσ*上增加了电子0.02908,电负性下降,能级上升至−0.41998。而·CH3的P型轨道失去电子0.02900,电负性上升,能级由−0.38557下降至−0.41998,从而达到了氢键两边的电负性均衡。
现在问题是,如果不是增加一个电子,而是微量电子,FHσ键外围空域的“能级”会有多高呢?
也不妨具体用χ* = (1 + q)χ推算一下。得到FH的LUMO在没有电子占据时的起始能级应为−0.4326。
在图4右边,甲基·CH3,2MO5是它的单电子,HOMO,它是一个P型轨道,正是它要受FHσ键在外围空域所形成的势阱的吸引,电子要向FH偏移,部分电子要落于这个势阱之中。额外的电子进入FHσ键外围空域,它将采取FHσ键在外围空域所形成的势阱LUMO大致形象,至于所处的“能级”高低则取决于进入外围空域FHσ*的电子量。
从图4左边看,势阱LUMO形象是F的P型和H的S型反相位分离对峙。·CH3的P型轨道电子平移过去时,与对方H的空位S型势阱对称性不符、正交,(这与双方都有电子时P型的一端与S型相位相符的组合成键不一样),偏移电子要落于这个势阱对称性相符的F上,MO10的形象正是这样,H上没有偏移电子,这就是形成氢键的MO。
MO10的形象表明,电子偏移锚定了共享电子空间。偏移电子也自然是电子共享的一部分。电子偏移向F而不是H,而这个举动使·CH3的P型单电子被拉入了电子共享成键区域。这包含了经典氢键概念认为H被双方电负性较强原子狭义静电作用吸引。而体系的共享电子吸引与双方电子排斥、核排斥的平衡,这都是静电作用。
只要有能级差可以发生电子偏移并锚定共享电子空间,即可形成广义的氢键,这样就把非经典的氢键体系、类氢键体系(锂键、鈉键、卤键)包括其中了。
当然MO10所展现的电子偏移能级下降并不是唯一的变化,由于·CH3移走电子,电子排斥减小,氢键中·CH3的各个MO的能级都有所下降。反之因FH接受了电子,电子排斥增大,氢键中FH的各个MO的能级都有所上升。虽然要综合地看总体的能量变化,但电子偏移、电子共享却是总体能量下降的主体、本源。
计算的氢键结合能为:0.004076 (10.84 kJ/mol)。双方相距(H⋯C) 2.49462。
氢键MO10能级为−0.41998,偏移电子正是落入了FHσ键外围的空域FHσ*。这使得FHσ键由自由状态到氢键中,些许电子进入反键轨道,键长由0.9145伸长至0.9188,振动频率由4220.85下降至4114.68。产生所谓红移。
电子偏移进入反键轨道产生红移氢键是一个普遍现象。
FHσ键1MO3,它被照搬到氢键体系中是MO5。
2.2.2. 以FH⋯HBeH为例
在众多的氢键算例中,能级较高部位的电子向能级较低部位转移部分电子,MO发生偏移,还是较为复杂的。上面FH⋯·CH3等例子,主要只一个MO电子发生偏移形成氢键,这里FH⋯HBeH [10] 例子,主要是两个MO相互发生偏移形成氢键。
FH⋯HBeH属于二氢键。曾几何时,二氢在分子之间也能构成氢键还是新鲜事,但在氢键新概念,它也是能级高位的电子(HBeH)要部分偏移到能级低位处(FH)的势阱中。
图5是相关的MO图。
中列是形成氢键的MO。
左列、右列是对应的FH和HBeH相关MO,列在图中的只是它们形成氢键的HBeH的P型电子与对称性相符FH的P型MO。其它与氢键生成没有直接关系,照搬到氢键体系中,没有列出。
图5中列MO8是HBeH的P型MO电子向FHσ空域偏移形成的氢键相关MO之一。
图5左列1MO3是一个F的P型轨道与H的S型形成的成键轨道,是一个变形扩展的P型轨道。
图5右列2MO3是Be的P型轨道分别与两个H的S形成的成键轨道之一,是一个变形扩展的P型轨道。
能级差距引起HBeH电子向FHσ偏移。当然不是偏移到1MO3上,因为2MO3与1MO3都是满占的配对电子,相互之间存在很强的Pauli互斥。而是偏移到1MO3周围空域即LUMO,FHσ*。
1MO3是FHσ键,在其周围的空域增加额外的电子是反键的FHσ*,即1MO6,它构成了一个与2MO3对称性相符的周围的空域。
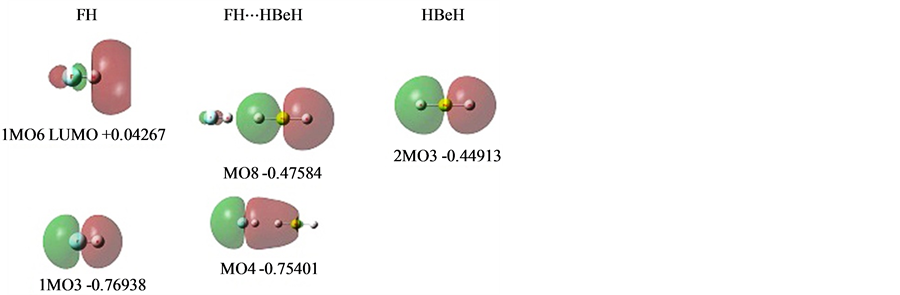
Figure 5. MOs of FH⋯HBeH
图5. FH⋯HBeH的MOs
从MO8看,由于电子进入FHσ*反相位空域,偏移电子与其母体是反相位的,表明这两部分电子之间是排斥的,继承了FHσ*的反键性质。这与双方的核吸引共享电子是同时存在的。前者是电子与电子的,后者是核与电子的,同时并存并不矛盾。
MO8的电子偏移量不能像上面那样通过电子密度差直接得出,因为密度差虽然在FHσ*上有确切的电子增值,但是氢键双方靠近时,双方满占的配对电子的Pauli互斥使得HBeH的电子也变形了,也产生了正负值,与FHσ*上的增值正值混淆在一起。这时需要在密度差的基础上进行“盆积分”[2] 。
这样得到的电子偏移量是0.01942。
但这电子偏移,又造成新的不平衡。这时,由于HBeH轨道本身失去了电子,能级下降,而外围空域FHσ*增加电子对其下FHσ轨道上电子发生排斥挤压,能级上升,这时FHσ轨道本身的电子偏移向了HBeH轨道。FH的Fp、Hs是相位相符的,与HBeH也是相位相符的。因为HBeH这里失去了电子,电子无需偏移到HBeH的外围反键空域,这次偏移是同相位的。这与上面是不同MO层次的事,形成了另一个分子轨道MO4,这是FH⋯HBeH氢键相关的轨道之二。用电子密度差方法可直接得到此次电子偏移量为0.02247。这时MO4的能级比1MO3还高,是生成MO8时1MO3已被抬高所致。
现在一方面HBeH向FHσ*空域偏移了电子,另一方面FHσ的偏移又向HBeH空域补充了电子,它们相互影响、互为因果,一次又一次地电子由能级高处流向能级低处。作为不同的MO,它们本是正交的,不会有电子混杂、交流,但是它们的电子与电子之间的静电作用还是能够相互影响和传递的。这时原子上电荷变化与电负性变化已经不是简单线性关系了。FH⋯HBeH最终给出了平衡共存的结果,我们看到的只是这最终平衡的结果,MO偏移的过程只是大致想象,它们应是同时发生并调整的。
计算氢键结合能为0.005016 (13.33 kJ/mole)。双方相距(H⋯H) 1.74457。
2.2.3. 以(HF)2为例
举了上面两个简单例子,明白了氢键体系中处于高能级的电子如何流向低处,这低处的原始起点又在何处,现在可以讨论通常经典的氢键了。
(HF)2是氢键的最初发现和研究时的种类,是氢键的典型,分子是如此地简单,但众多的MO乍一看还真有点眼花缭乱,有了上面例子现在就好说了。
图6中列是(HF)2的MO图,左右两列是两个HF对应MO图。这三者的内层1s、2s的MO分别从两个HF照搬到(HF)2之中都没有列出。这次因为涉及到孤对电子n,4个n都列出了,4个中的3个也基本不变照搬到(HF)2之中了,这里可以看到是如何照搬的。
从图6看,(HF)2的MO列出了6个,还有4个内层轨道没列出。列出的6个中,有3个n也基本上
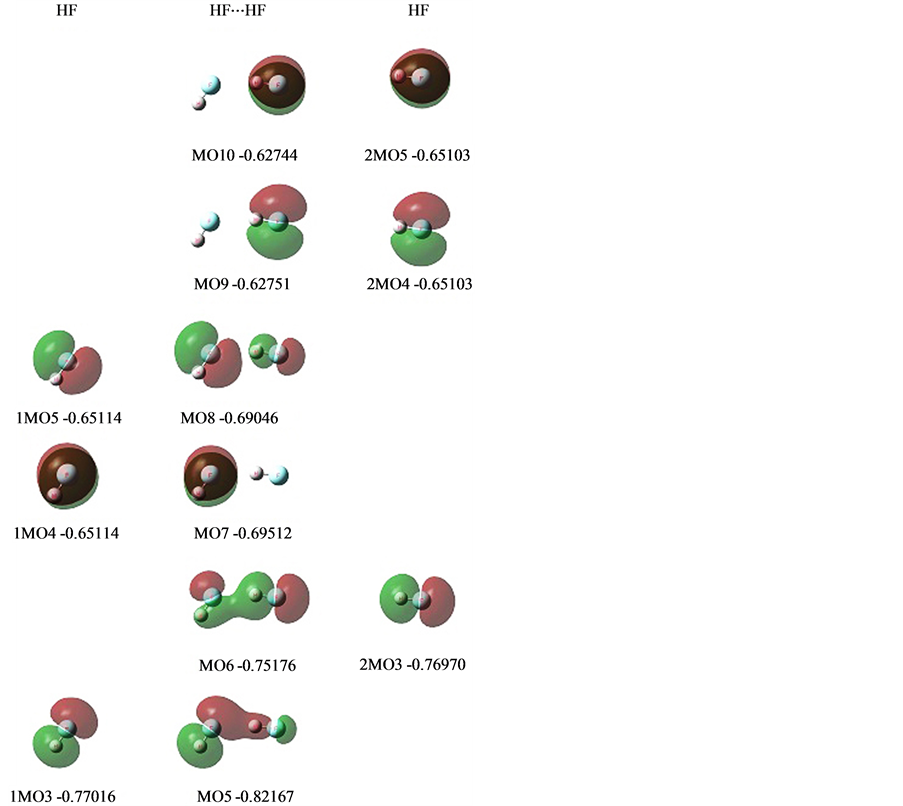
Figure 6. MOs of (HF)2
图6. (HF)2的MOs
没有变化照搬到体系中的,只是能级有所沉浮。真正与形成氢键相关的有3个MO。
与氢键形成相关的3个MO分别是:
第一是MO8。它是孤对电子1MO5受2MO3,FHσ键周围空域势阱吸引电子发生偏移形成的。它的电子偏移量是0.2743。这周围空域势阱具有反键性质(见图5的1MO6,即FHσ*),F的P型和H的S型反相位分离对峙,n(1MO5)偏移电子到相位相符的F的P型上,n主体与偏移电子相位相反,体现了这个空域的反键性质。
第二是MO6。MO8所发生的电子偏移,导致n(1MO5)本身电子缺失,吸引电子的能力大增,以至FHσ键2MO3要向1MO5空域发生电子偏移。它的电子偏移量是0.3631。成键的2MO3是相位相符的F的P型和H的S型所形成的P型,偏移到n(1MO5)缺失电子的空域,这时MO6在连接两个HF之间是同相位的。
第三是MO5。2MO3电子发生偏移使它的能级下降,而n(1MO5)补充了电子对FHσ键1MO3发生挤压,以至1MO3要向2MO3的空域发生电子偏移。它的电子偏移量约是0.1695。这时MO5在连接两个HF之间是同相位的。
这三个MO,虽然上面第一、二、三地讨论了相互影响引起电子偏移,但是他们不会是这样循序完成的。它们相互影响,电子流向有来有往,在能量的低谷处达到平衡,从而拉近、锚定了双方,构成了电子共享区,电子在核间就是这样分布能量才最低,低过了两个HF能量的加和,从而形成了氢键的能量:19.71 kJ/mol。这能量对抗了氢键双方拉近时增加的电子与电子、核与核的排斥力。双方相距(F⋯H)1.84233。我们看到的只是最终平衡的结果,MO偏移的过程只是大致想象,应是同时发生的。
平常对这种轨道之间的关联,说是轨道相互作用,其实当轨道上电子发生偏移,进入到对方的空域时,它必须采用对方的空域性质,即对方的基组线性组合,并不是对方真提供了这么多电子在一起来形成MO。因为它们都是稳定的配对电子,相互之间存在较大的Pauli互斥,并不会掺合在一起形成轨道。但相互之间有能级差,电负性差,MO中会发生电子偏移,以至部分电子会落入对方的势阱之中,从而调平双方的电负性,达到电负性均衡。
能级差引起的双方静电引力拉近了双方的距离,产生了电子偏移,构成了共享电子空间,这是氢键结合力的来源。
如果认为(HF)2主要只是狭义的静电作用,会是负得最多的F端与另一方正得最多的H端以直线组合为最佳。然而实验和计算的氢键构成都是图6的孤对电子偏移式。能级更高的孤对电子偏移式比直线式总能量低(下降了−3.46 kJ/mol),氢键距离要短0.12131。这表明能级差距才是氢键生成的动力。
2.3. 新概念下其它各种氢键的例子
2.3.1. 经典氢键(H2O)2的例子
见图7。这里,基本上没有变化照搬到氢键体系中,只是能级有所沉浮的MO都没有列出。
对于一个H2O来说,实际上参与形成氢键的MO可以分成两种,一种是孤对电子,另一种是HO的σ键所钩成的MO,这两种MO虽然都是P型,但在一个H2O中却是正交的,只是在(H2O)2中,两个H2O取一定的角度才成为非正交。
正交的MO虽然不能直接发生作用转移电子,但是它们周围电子的增减变化引起的静电排斥变化,仍然可以影响与之正交MO能级发生沉浮。
形成氢键作用的有4个MO,可以观察到的是:
依次是MO9、MO8、MO7、MO6。
在构成氢键分子时,1MO6与2MO4相遇,它们都是配对的键电子,有斥力,于是它们先同相位地构成MO8,然后反相位地生成MO9。
当1MO4与2MO3相遇,它们也都是配对的键电子,于是它们先同相位地构成MO6,然后反相位地生成MO7。
这里,与通常的成键形成MO的规律是一样的。但MO9显然也属于高能级的电子向低能级势阱的偏移。但这两种解释却是不尽相同的,它们如何统一,还需要进一步探讨。
但电子就是这样安排,在能量的低谷达到平衡,电子在核间就是这样分布能量才最低,低过了两个H2O能量的加和,从而形成了氢键的能量:24.42 kJ/mol。这能量对抗了氢键双方拉近时增加的电子与电子、核与核的排斥力。双方相距(O⋯H) 1.97738。
(HF)2和(H2O)2,是经典氢键的典型,同样在这种处于能级高位的电子偏移向能级低位,多层次地调整电子分布以达到电负性均衡,也是氢键的典型。
2.3.2. π型氢键:CHCHπ⋯HF
CHCHπ⋯HF [11] 的MOs见图8。这里HC≡CH的π电子处于能级的高位,要向能级低处偏移电子。只列出了形成氢键的相关MO。

Figure 7. MOs of (H2O)2
图7. (H2O)2的MOs

Figure 8. MOs of CHCHπ⋯HF
图8. CHCHπ⋯HF的MOs
第一是MO11。是处于能级的高位的HC≡CH的π电子1MO7向2MO3外围空域HFσ* (2MO6,LUMO)偏移电子形成的。电子偏移量为0.04775。电子偏移部分与原本体部分查呈现反相位。
第二是MO7。上面的电子偏移,导致了新的不平衡,引起了新的电子偏移,2MO3向1MO7补充过来电子,电子偏移量为0.01649。电子偏移部分与原本体部分呈现同相位。
或者理解为1MO7与2MO3相遇,同相位地构成MO7,又因为它们都是配对的键电子,有斥力,又反相位地构成MO11。
体系的氢键的能量:24.42 kJ/mol。双方相距(CCπ中点⋯ H) 2.2486。
2.3.3. 分子内氢键:甲醛OCH2
在氢键新概念,甲醛OCH2属于分子内氢键。
图9是相关的MO图。
中间是形成氢键的MO。
左边、右边是形成氢键的O的n和CH2的P型MO。其它与氢键对称性不符、正交的MO,照搬到氢键体系中,没有列出。当然自由的O和CH2还不是OCH2中成键形态的,只是借用来做参考。
图9中列MO8是氢键相关MO之一。
图9左列就是O的n的形象,是一个P型MO。由于O在OCH2中从σ键、π键吸引过来较多电子,n电子能级被抬得很高,CH2失去电子能级下降,引起O的n电子向CH2的P型势阱偏移。当然不是偏移到CH2上,因为O的n与CH2都是满占的配对电子,相互之间存在很强的Pauli互斥。而是偏移到CH2周围相位相同的P型空域,即2MO7,是LUMO+1,它是反相位的。
从MO8看,由于电子进入CH2的外围P型为反相位空域,O的n与CH2的外围P型是反相位的,它表明MO8两部分电子之间是排斥的,这与双方的核吸引共享电子是同时存在的情况。 前者是电子与电子的,后者是核与电子的,同时并存并不矛盾。
由于表面看是电负性高的O向电负性低的CH2偏移了电子,文献称此类情形为“π电子反馈”。
图9右列2MO3是CH2的P型轨道。如此之大的电子偏移,又造成新的不平衡。CH2的P型空域接受了电子,CH2受到挤压,能级升高。而O的n偏移走了电子能级却下降。这次,CH2本身的电子要偏移向了O的n的空域了。
因为O的n这里失去了电子,电子无需偏移到O的n的外围反键空域,这次偏移是同相位的。这是另一个层次的事,形成了另一个分子轨道MO5,这是OCH2氢键相关轨道之二。
由于表面看是O的n与σ键体系的CH2形成了共轭,文献称此类情形为“超共轭”。
或者理解为1MO5与2MO3相遇,同相位地构成MO5,又因为它们是配对的键电子、孤对电子,有斥力,又反相位地构成MO8。
这里的MO构成与氢键MO构成是基本相同的,所以认为是一种氢键,分子内氢键。后文还要进一步讨论甲醛OCH2作为分子内氢键的特性。
2.3.4. 锂键:H3CLi⋯·CH3
H3CLi⋯·CH3 [12] 是一个单电子锂键。C-Li是双电子σ键,键长1.99569,Li⋯·C是单电子氢键,双方相距(Li⋯·C)2.40880。能级高位甲基单电子向处于能级低位的锂键端头空域偏移电子。
相关的MO见图10。但从图看,1MO6比2MO5的能级还高,如何确定能级低位呢?
说一个MO有一个能级值,其实它只是该电子一个空间分布的统计平均值,并不是在任何部位都只有这一个固定的值。
从电负性的视角来看,在空间某一点电子密度ρ,是电子在这一点的概率密度,其实ρ准确地给出了该点吸引电子的能力,就可以表征该点的电负性。
当看一个MO的电子密度ρ图时,就是在看这MO每一个点的电负性图,比如1MO6这个H3C-Li键,由于Li的电负性远小于H3C-,在成键中Li有大量的电子被转移走了,以至于Li向外的端头严重裸露,正像H的境遇一样。-Li向外的端头电负性很高,形成了一个低能的势阱。正是这个低能势阱,接受了甲基单电子。
在与H3C-成键时,-Li采取了SP型杂化,杂化的大瓣向着H3C-,这是-Li供出电子的结果。
而在H3CLi与甲基·CH3对接时,由于·CH3对接在H3CLi的端头SP型杂化空域,而不是H3CLi的反

Figure 9. MOs of OCH2
图9. OCH2的MOs
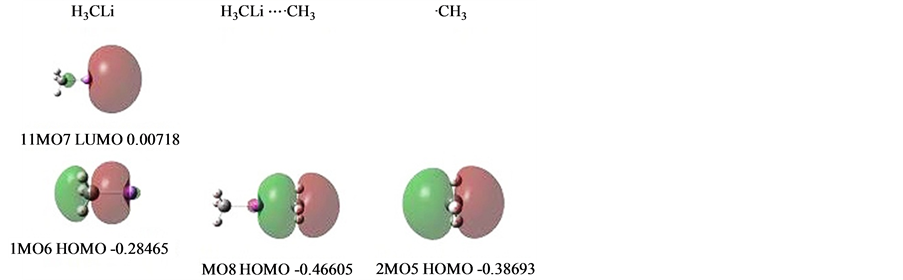
Figure 10. MOs of H3CLi-CH3
图10. H3CLi-CH3的MOs
键空域,H3CLi⋯·CH3的氢键形象MO8是同相位的。即偏移电子与单电子本体是同相位相连接的。这体现Li受双方吸引,与双方分别共享电子,只是一边是双电子σ键,一边是单电子氢键。
现在知道1MO6这个H3C-Li键的能级,它的端头能级曾经低到什么程度呢,现在知道氢键形成之后,氢键中单电子能级由−0.38693下降至−0.46605。电子偏移量约为0.04568,同样用χ* = (1 + q)χ推算,得到H3C-Li端头势阱为−0.4683。
H3CLi⋯·CH的氢键结合能为26.31 kJ/mol。
2.3.5. 卤键: H3C·⋯ClF
在H3C·⋯ClF [13] ,双卤分子ClF提供了一个低能级势阱,接受能级高位的甲基单电子,见图11。
甲基H3C的单电子1MO5,受ClFσ低能级势阱的吸引,在它的外围空域2MO14即ClFσ*偏移电子,形成氢键轨道MO18。
偏移电子量用电子密度差计算为−0.03129,+0.03136。推算ClFσ*在完全没有电子时能级为−0.4194。当它接受了0.03136电子后,能级升至−0.40604。
计算得到的卤氢键结合能为8.119 kJ/mol。双方相距(C·⋯Cl) 3.03598。
2.4. 再说氢键新概念
第一、氢键的所有例子,都表明能级差距引起的电子偏移,能量降低,形成了氢键双方的电子共享,所以氢键形成的机制大体也就是在此。
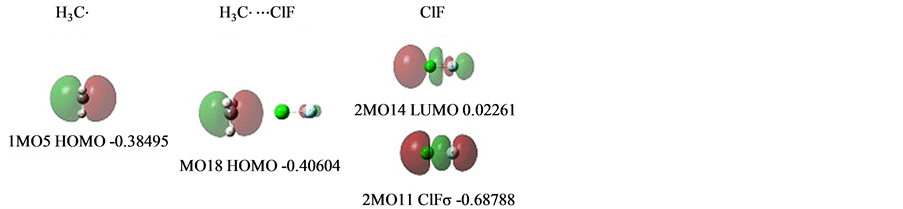
Figure 11. MOs of H3C-ClF
图11. H3C-ClF的MOs
第二、处于能级较高部位的电子,如HOMO,主要是指非键的孤对电子、单电子,还有键电子,如π、σ电子。由于这些电子如孤对电子,所在的原子电负性相对较高,在分子中成键时吸引过来较多电子,使得孤对电子的能级被抬得很高。比如水分子的孤对电子在静电势图中呈现红色,为负值,易于给出电子使体系能量降低。
同时,处于能级较低部位的如LUMO所在的主要原子电负性也较高,有利于形成能量较低的势阱,易于接受电子。
这些与经典氢键概念认为在氢键X-H…Y体系之中,X、Y的电负性高利于生成氢键的经验归纳是一致的。
第三、电子从高位向低位的偏移形成氢键,形成电子共享区域,这偏移电子有些还落入对方势阱之中,这种情景氢键自然就既有共价作用又有狭义静电作用,同时共存。
对氢键这种情景量子化学作了精确计算。也得到了实测的支持。
图12,是中科院国家纳米科学中心的科研人员,在国际上首次“拍到”的氢键“照片”,它实现了氢键的实空间成像[14] 。这是8-羟基喹啉分子之间的氢键。氢键是黄色的亮线条,它表明氢键上是有电子出没在核之间形成共享的。如果纯粹是狭义的静电作用,核之间是不会呈现这种线性形态的电子分布的,这正是共价性质的特征。氢键应是弱化学键。
第四、从上面各种例子可以看到,偏移的电子量,或大或小,它只表明平衡某次双方的电负性所需要的电子量,表明电负性平衡之前双方电负性的差距。当然这差距正是拉近双方、电子偏移的原动力,也与氢键结合能相关,但是氢键结合能还有更多的内容。
不能直接仅将偏移电子量与结合能挂钩,因为偏移电子量只是电子共享量中的一小部分,且与氢键结合能没有数量上的因果关系。
第五、通常在双方都是单电子成共价键时,MO系数都是代表双方实有电子的,还包括转移电子。
在氢键格局中,把双方的所谓轨道相互作用,判定为甲方处以高位的电子向乙方处于低位的势阱发生偏移。这势阱本是虚位以待的,势阱这里产生的轨道相互作用波函数值,实际上是甲方偏移电子到乙方势阱,必须取乙方空域所形成势阱的波函数。并不是乙方真有这么多轨道电子去与甲方发生轨道相互作用并组成氢键分子轨道,因为在形成氢键时,接受电子的对应方已是稳定的价键,是电子配对的MO,对外来电子斥力较大,只能拉开距离,在它的外围空域势阱偏移电子,构成电子共享,形成弱键。
第六、任一个MO的电子,在各个核所生成的势阱之中,要受分子全部核和电子的作用的。其实还应包含势阱中的电子自身的作用。因为在势阱中的电子是波、是同时无处不在的,每一个时刻势阱中的电子不是一个点,而是全空间。对于每一个MO,任一点的电子密度ρ竟是以它自己其它所有ρ同时存在为前提的。势阱中的任一处出现的电子是要受到势阱中其它各处电子自己所作用的,即电子对电子的排斥、电子对核的屏蔽。这个MO的ρ的空间分布体现电子自己排斥自己,电子自己屏蔽自己。

Figure 12. Pictures of hydrogen bond
图12. 氢键的照片
(待续。这里只是整篇文章的前一部分,有待下文:更多的氢键例子;氢键新概念对以往氢键研究成果的继承、包容和发展;氢键新概念对蓝移氢键等一些问题的分析讨论)。
文章引用
周光耀, (2015) 氢键的量子化学研究(一)
A Quantum Chemistry Study of Hydrogen Bonds (1). 物理化学进展,02,84-101. doi: 10.12677/JAPC.2015.42011
参考文献 (References)
- 1. The Gordon Research Group: The General Atomic and Molecular Electronic Structure System (GAMESS) is a general ab initio quantum chemistry package. http://www.msg.chem.iastate.edu/gamess/
- 2. Lu, T. and Chen, F.W. (2012) Multiwfn: A multifunctional wavefunction analyzer. Journal of Computational Chemistry, 33, 580-592.
- 3. University of Illinois at Urbana-Champaign, VMD Visualar Molecular Dynamics. http://www.ks.uiuc.edu/Research/vmd/
- 4. Parr, R.G., Donnelly, R.A., Levy, M. and Palke, W.E. (2007) Electrone-gativity equalization method: Parameterization and validation for large sets of organic, organohalogene and organometal molecule. International Journal of Molecular Sciences, 8, 572-582.
- 5. Sanderson, R.T. (1951) An interpretation of bond lengths and a classification of bonds. Science, 114, 670-672.
- 6. 周光耀 (1985) 关于电负性均衡原理. 化学学报, 43, 1-3.
- 7. 周光耀 (2014) 范德华作用的量子化学研究(四). 物理化学进展, 3, 1-10.
- 8. Misochko, E.Y., Benderskii, V.A., Goldschleger, A.U., Akimov, A.V. and Shestakov, A.F. (1995) Formation of the CH3-HF complex in reaction of thermal F atoms with CH4 in solid Ar. Journal of the American Chemical Society, 117, 11997.
- 9. 王海燕, 曾艳丽, 孟令鹏, 郑世钧 (2005) 有关氢键理论研究的现状及前景. 河北师范大学学报(自然科学版), 29, 177-181.
- 10. 吴志坚, 吴季怀 (2006) 二氢键. 大学化学, 26, 33-37.
- 11. Stefov, V., Pejov, L. and Loptrajanov, B. (2003) Experimental and quantum chemical study of pyrrole self-association through N—H ⋯π hydrogen bonding. Journal of Molecular Structure, 649, 231-243.
- 12. 李志锋, 朱元成, 左国防, 唐慧安, 李红玉 (2010) 反常蓝移单电子锂键Y…Li—CH3[Y=CH3, CH2CH3, CH(CH3)2,C(CH3)3]体系的结构与性质. 物理化学学报, 26, 429-435.
- 13. Legon, A.C. (1999) Prereactive Complexes of Dihalogens XY with Lewis Bases B in the Gas Phase: A Systematic Case for the Halogen Analogue B small middle dot small middle dot small middle dotXY of the Hydrogen Bond B small middle dot small middle dot small middle dotHX. Angewandte Chemie International Edition (Engl.), 38, 2686- 2714.
- 14. 李大庆 我科学家用高分辨原子力显微镜率先“看见”氢键. 光明网, 2013-11-23. http://tech.gmw.cn/2013-11/23/content_9579493.htm