Advances in Applied Mathematics
Vol.04 No.01(2015), Article ID:14884,5
pages
10.12677/AAM.2015.41009
An Extragradient Algorithm for Quasi-Variat-Ional Inequality Problem
Yuanyuan Yuan, Wenwei Zhang, Biao Qu
School of Management, Qufu Normal University, Rizhao Shandong
Email: shuijing_0622@126.com
Received: Feb. 8th, 2015; accepted: Feb. 21st, 2015; published: Feb. 27th, 2015
Copyright © 2015 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
In this paper, we present a projection-like algorithm for solving the quasi-variational inequality problem. In the second projection step of the algorithm, we replace the orthogonal projection onto a general closed convex set with a projection onto a halfspace, which reduces the difficulty of calculation to some extent. The global convergence of the algorithm is given.
Keywords:Quasi-Variational Inequality, Projection, Extragradient
求解拟变分不等式问题的一种外梯度算法
袁媛媛,张文伟,屈彪
曲阜师范大学管理学院,山东 日照
Email: shuijing_0622@126.com
收稿日期:2015年2月8日;录用日期:2015年2月21日;发布日期:2015年2月27日

摘 要
本文给出了求解拟变分不等式问题的一种投影算法,在算法的第二次投影步中,把到一般闭凸集上的投影松弛为到半空间的投影,这在一定程度上减少了计算的难度。该算法的全局收敛性得到证明。
关键词 :拟变分不等式,投影,外梯度

1. 引言
给定一个向量值函数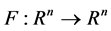 和一个集值函数
和一个集值函数 ,拟变分不等式问题
,拟变分不等式问题 就是求一个向量
就是求一个向量 ,使得
,使得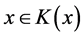 ,且满足
,且满足
 (1.1)
(1.1)
其中 表示
表示 中所有子集所形成的集合,
中所有子集所形成的集合, 表示
表示 中的内积。
中的内积。
拟变分不等式问题在经济、工程、最优化和控制等领域都有着广泛的应用。例如经济问题中的Nash均衡问题可以等价地转化为一个变分不等式问题,而广义Nash均衡问题可以等价地转化为一个拟变分不等式问题[1] 。两者比较而言,广义Nash均衡问题更接近经济问题的实际。因此,研究拟变分不等式问题的有效数值解法有着重要的理论意义和实用价值。对于拟变分不等式问题的研究,正如文献[2] 所言:“the study of the QVI to date is in its infancy at best”。因此,寻找和设计求解拟变分不等式问题的算法是很有意义的工作。在求解拟变分不等式问题的算法方面,文献[3] 提出了两步投影法,即:每次迭代需要计算预测步和校正步;文献[4] 在假设算子具有协强制性条件下,对[3] 中的算法做了改进,并给出了收敛性分析。另外,文献[5] 也给出了投影类算法。在上述已有的投影类算法中,所有的投影都是到由当前迭代点所产生的一个闭凸集上或原问题的可行解集上。我们知道,到一般闭凸集上的投影有时不易求得或者很难计算。受文献[6] 求解变分不等式问题算法的启发,我们设计了求解拟变分不等式问题的一种投影算法,在算法的校正步中,我们把到一般闭凸集上的投影松弛为到半空间的投影,而这里构造半空间时,还成功避免了次梯度的求解,这在一定程度上减少了计算的难度。
2. 预备知识
本节中,我们将给出算法及证明中所用到的定义、引理、假设条件等。
对于给定的非空闭凸集 ,从点
,从点 到
到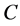 的正交投影(以下我们简称投影)定义为:
的正交投影(以下我们简称投影)定义为:

它有如下性质:
引理2.1 [7] :设集合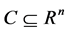 为非空闭凸集,则对
为非空闭凸集,则对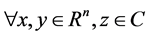 ,有下列不等式成立:
,有下列不等式成立:
(1)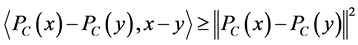 ;
;
(2) ;
;
(3) .
.
由引理2.1之(1)知,投影算子 具有非扩张性,即:对任意的
具有非扩张性,即:对任意的 ,有
,有

设 是
是 的一个映射,对任意的
的一个映射,对任意的 和
和 ,定义:
,定义:

引理2.2 [8] :设 是
是 的一个连续映射,则对任意的
的一个连续映射,则对任意的 和
和 ,有
,有

下面我们给出几个有关点集映射的定义:
定义2.1:令 ,则映射
,则映射 称
称
(1) 在 处上半连续,若
处上半连续,若

(2) 在 处下半连续,若对任意满足
处下半连续,若对任意满足 的点列,
的点列, ,及满足
,及满足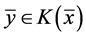 ,均存在一点列
,均存在一点列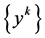 ,使得当
,使得当 ,且
,且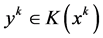 成立;
成立;
(3) 在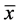 处连续,若在
处连续,若在 处既上半连续,又下半连续;
处既上半连续,又下半连续;
(4) 在集合 上连续,当且仅当在
上连续,当且仅当在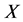 上的每一点都连续。
上的每一点都连续。
在本文中我们做如下假设:
假设(H)
(a) ,对
,对 ,有
,有 ;
;
(b) 若 是
是 的一个解,则对
的一个解,则对 ,有
,有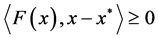 ;
;
(c) 在
在 上连续;
上连续;
(d) 函数 是
是 连续的,即对
连续的,即对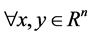 ,
, ,满足:
,满足:

3. 算法及其收敛性分析
算法3.1
步骤0:给定常数 置
置 ,选定任意的初始点
,选定任意的初始点 ,令
,令 。
。
步骤1:根据当前迭代点 ,计算
,计算
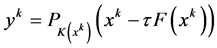
步骤2:构造半空间 ,
,
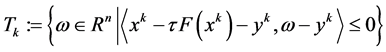
步骤3:计算下一步迭代点,

步骤4:如果 ,停止。否则,令
,停止。否则,令 ,转到步骤1。
,转到步骤1。
注:(1) .
.
这是因为: ,故对
,故对 由投影性质得:
由投影性质得:

因此 ,从而有
,从而有 。
。
(2) 若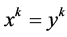 ,则
,则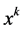 是
是 的一个解。
的一个解。
事实上,如果 ,则
,则 ,所以
,所以 。
。
由投影性质: ,得
,得

又因为 ,故有下式成立:
,故有下式成立:

从而 是
是 的一个解.
的一个解.
定理3.1:若假设条件(H)成立, 是由算法3.1产生的迭代点列,则
是由算法3.1产生的迭代点列,则 收敛到
收敛到 (1.1)的一个解。
(1.1)的一个解。
证明:取 是
是 (1.1)的一个解,由假设条件(a):
(1.1)的一个解,由假设条件(a): ,从而
,从而 ,故
,故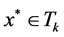 。
。
对 ,有
,有 ,由假设条件(b)得,
,由假设条件(b)得,
 (3.1)
(3.1)
根据引理2.1(2)和(3),(3.1)式及假设条件(d),我们得到:

由于 ,故
,故 单调递减,从而收敛,所以,序列
单调递减,从而收敛,所以,序列 有界。另外,由上式得:
有界。另外,由上式得:
 (3.2)
(3.2)
假设 是
是 的一个聚点,则必存在收敛子列
的一个聚点,则必存在收敛子列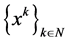 ,使得:
,使得:

这里 。下面我们来证明
。下面我们来证明 是
是 (1.1)的一个解。
(1.1)的一个解。
首先证明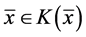 。由(3.2)式得:
。由(3.2)式得:

再由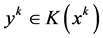 及
及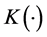 的上半连续性,即得:
的上半连续性,即得: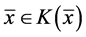 。
。
下面我们来证明: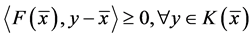 。
。
由于 是下半连续的,那么,对
是下半连续的,那么,对 ,存在一个序列
,存在一个序列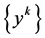 ,
, ,使得
,使得 。令
。令 ,则由引理2.2及(3.2)得:
,则由引理2.2及(3.2)得:
 (3.3)
(3.3)
由 可得:
可得:

即

令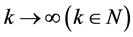 ,由
,由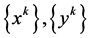 的有界性及(3.3),我们得到
的有界性及(3.3),我们得到

由 的任意性,得到了我们所要证明的结论.
的任意性,得到了我们所要证明的结论.
综上知, 是
是 (1.1)的一个解。用
(1.1)的一个解。用 代替上述证明中的
代替上述证明中的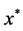 ,则得
,则得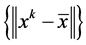 是收敛的。而此时已知有一子列收敛到0,故整个点列
是收敛的。而此时已知有一子列收敛到0,故整个点列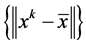 是收敛到0的,即
是收敛到0的,即 收敛到
收敛到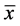 。定理得证!
。定理得证!
4. 数值实验
为了验证本文所给算法的可行性和有效性,我们通过MATLAB用它解决了一个广义纳什均衡问题转化成的拟变分不等式问题。在计算过程中,算法的参数取为: ,
,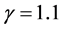 ,
, ,
,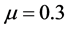 ,
, ,
, 。在下面的数值结果中,所有的CPU时间按秒记,近似解指最后一个迭代点,最大迭代步数限定为1000步。
。在下面的数值结果中,所有的CPU时间按秒记,近似解指最后一个迭代点,最大迭代步数限定为1000步。
例1:此例是一个广义纳什均衡问题,首次出现在文献[9] 和[10] 中,也曾在[3] 中被引用过。该问题是一个两人对策,每个人选取0到10之间的一个数 ,并且它们的和不能超过15。费用函数和映射
,并且它们的和不能超过15。费用函数和映射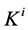 定义如下:
定义如下:

Table 1. The resulting data of numerical experiment
表1. 数值实验数据结果
现在考虑此问题的 形式,函数
形式,函数 定义为:
定义为:

它的解组成如下:点 及线段
及线段 。从不同的初始点出发,用算法3.1得到的数值结果如表1所示。
。从不同的初始点出发,用算法3.1得到的数值结果如表1所示。
可以看出,从不同的初始点出发,用算法3.1都能得到原问题的解。
基金项目
本文为国家自然科学基金(11271226)和山东省优秀中青年科学家科研奖励基金(BS2012SF027)资助项目。
文章引用
袁媛媛,张文伟,屈 彪, (2015) 求解拟变分不等式问题的一种外梯度算法
An Extragradient Algorithm for Quasi-Variat-Ional Inequality Problem. 应用数学进展,01,70-75. doi: 10.12677/AAM.2015.41009
参考文献 (References)
- 1. Harker, P. (1991) Generalized Nash games and quasi-variational inequalities. European Journal of Operational Research, 54, 81-94.
- 2. Pang, J.S. and Fukushima, M. (2005) Quasi-variational inequalities, generalized Nash equilibria and multileader-Fol- lower game. Computational Management Science, 1, 21-56.
- 3. Zhang, J.Z., Qu, B. and Xiu, N.H. (2010) Some projection-like methods for the generalized Nash equilibria. Computational Optimization and Applications, 45, 89-109.
- 4. Han, D., Zhang, H., Qian, G. and Xu, L. (2012) An improved two-step method for solving generalized Nash equilibrium problems. European Journal of Operational Research, 216, 613-623.
- 5. 屈彪, 张善美 (2008) 求解拟变分不等式问题的一种投影算法. 应用数学学报, 5, 922-928.
- 6. Censor, Y., Gibali, A. and Reich, S. (2011) The subgradient extragradient method for solving variational inequlities in Hilbert space. Journal of Optimization Theory and Applications, 148, 318-335.
- 7. Zarantonello, E.H. (1971) Projections on convex sets in Hilbert space and spectral theory. In: Zarantonello, E.H., Ed., Contributions to Nonlinear Functional Analysis, American Academic Press, New York, 19-32.
- 8. Gafni, E.M. and Bertsekas, D.P. (1984) Two-metric projection problems and descent methods for asymmetric variational inequality problems. Math. Program, 53, 99-110.
- 9. Haker, P.T. (1991) Generalized Nash games and quasi-variational inequalities. European Journal of Operational Research, 54, 81-94.
- 10. Outrata, J. and Zowe, J. (1995) A numerical approach to optimization problems with variational inequality constraints. Mathematical Programming, 68, 105-130.
