Advances in Applied Mathematics
Vol.04 No.02(2015), Article ID:15213,6
pages
10.12677/AAM.2015.42018
Blowup of Solutions for a System of Doubly Nonlinear Degenerate Parabolic Equations with p-Laplacian
Longfei Qi, Jing Su, Qingying Hu
College of Science, Henan University of Technology, Zhengzhou Henan
Email: slxhqy@163.com
Received: Apr. 24th, 2015; accepted: May 7th, 2015; published: May 13th, 2015
Copyright © 2015 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
This paper is concerned with a system of doubly nonlinear degenerate parabolic equations with p-Laplacian. We prove that, under suitable conditions on the nonlinearity and certain initial datum, the lower bound for the blowup time is given if blowup does occur by using a modification of Levine’s concavity method.
Keywords:Blowup of Solution, Doubly Nonlinear Parabolic Equations, Levine’s Concavity Method
多重非线性退化的p-Laplacian抛物方程组解的爆破
齐龙飞,苏璟,呼青英
河南工业大学理学院,河南 郑州
Email: slxhqy@163.com
收稿日期:2015年4月24日;录用日期:2015年5月7日;发布日期:2015年5月13日

摘 要
本文研究了一类多重非线性退化的p-Laplacian抛物方程组解的爆破,利用修正的Levine凸性方法,在非线性项和初始条件的适当条件下,给出了解爆破时间的下界。
关键词 :爆破,多重非线性抛物方程组,Levine凸性方法

1. 引言
本文研究如下非线性抛物方程组解的爆破性
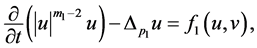 (1.1)
(1.1)
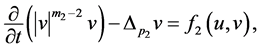 (1.2)
(1.2)
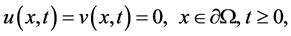 (1.3)
(1.3)
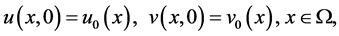 (1.4)
(1.4)
其中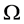 是
是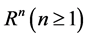 上的有界区域且有光滑边界
上的有界区域且有光滑边界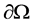 ,
,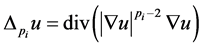 ,
,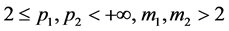 ,
,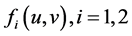 为以后给定的函数,
为以后给定的函数,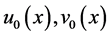 为正的初始函数。
为正的初始函数。
近几十年来,非线性抛物方程解的爆破问题引起人们的极大兴趣,考虑爆破性自然要研究解是否会爆破以及解的爆破时间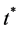 ,在这方面已经有大量的文献,如文献[1] -[5] 。问题(1.1)~(1.4)可以描述诸多化学反应、热传导过程和种群动力学过程(见文献 [6] - [17] 及其参考文献),它有多个非线性项,处理难度较大。对型如(1.1)的单个多重非线性抛物方程
,在这方面已经有大量的文献,如文献[1] -[5] 。问题(1.1)~(1.4)可以描述诸多化学反应、热传导过程和种群动力学过程(见文献 [6] - [17] 及其参考文献),它有多个非线性项,处理难度较大。对型如(1.1)的单个多重非线性抛物方程
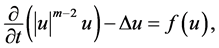 (1.5)
(1.5)
已有许多结果,如文献 [6] - [10] 给出了方程(1.5)的初边值问题和初值问题局部和整体解的存在性,文献 [11] - [14] 则研究了其整体吸引子的存在性和正则性,类似方程(1.1),(1.2)的方程组问题的整体吸引子的存在性和正则性也有一些研究 [15] - [17] 。但关于该类问题解的爆破性研究则相对较少,Iami和Mochizuki [18] 给出了Neumann初边值条件下方程(1.5)的爆破条件,Levine [19] - [21] 则用凸性方法证明了单个方程(1.1)及其等价的如下问题解的爆破性
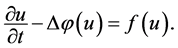
Korpusov和Sveshnikov [22] [23] 及Polat [24] 则对如下方程的初边值问题
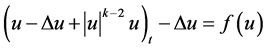
在负初始能量时得到解的爆破条件。Wang和Ge [25] 及其参考文献则利用比较原理讨论了非线性边界时方程(1.1),(1.2)中非线性项为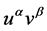 时解的爆破问题。
时解的爆破问题。
本文利用修正的Levine凸性方法讨论问题(1.1)~(1.4)解的爆破条件,推广了文献 [22] - [25] 的结果。在第二节将给出一些假设和基本引理,第三节给出主要结果和证明。
2. 假设和引理
本文所用符号均同文献 [6] ,记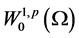 和
和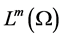 为通常的Soblev空间,其范数分别记为
为通常的Soblev空间,其范数分别记为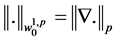 和
和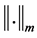 ,特别是当
,特别是当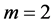 时,记
时,记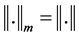 。
。
本文始终假设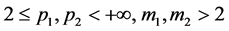 。关于非线性项
。关于非线性项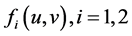 的假设如下:
的假设如下:
(A1)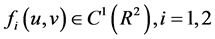 ,存在函数
,存在函数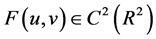 使得
使得
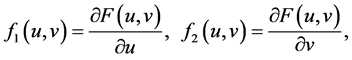
且存在常数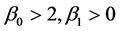 使得
使得
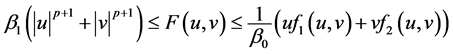 ,
,
其中,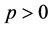 当
当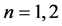 时,
时,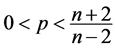 当
当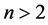 时。
时。
注:满足条件(A1)的函数是存在的。事实上,一个典型的例子是取
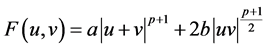
且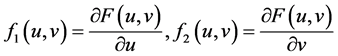 ,即
,即
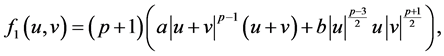
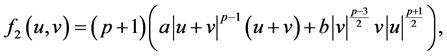
这时, 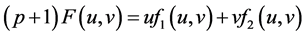 ,其中
,其中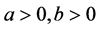 ,
,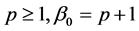 。该例的详细情况可见文献 [26] 。
。该例的详细情况可见文献 [26] 。
利用Galerkin方法,结合单调性理论和紧性方法 [2] ,类似文献 [27] 可得问题(1.1)~(1.4)解的局部存在性。
定理2.1. 假设条件(A1)成立且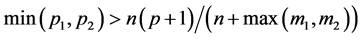 ,
,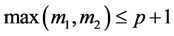 ,
,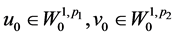 ,则问题(1.1)~(1.4)存在弱解
,则问题(1.1)~(1.4)存在弱解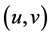 ,即,存在
,即,存在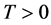 使得
使得
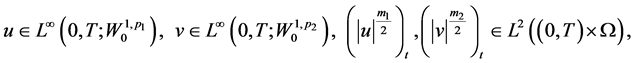
且对任意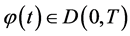 和任意分别的
和任意分别的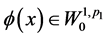 (或
(或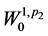 )成立:
)成立:
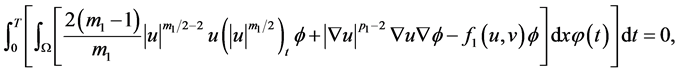
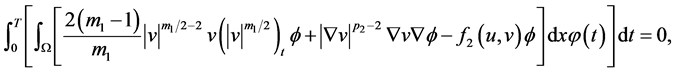
以及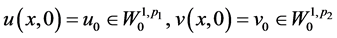 。
。
下面给出本文的基本引理。
引理2.2. [5] [27] 设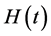 是R上非负二次连续可导函数且满足不等式
是R上非负二次连续可导函数且满足不等式
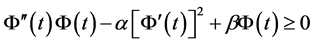
其中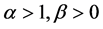 为常数。若
为常数。若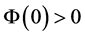 ,
,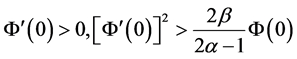 ,则必存在时刻
,则必存在时刻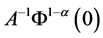
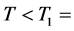 ,使当
,使当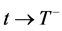 时有
时有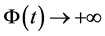 ,其中
,其中
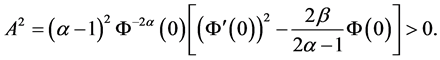
3. 主要结果及证明
首先引入泛函
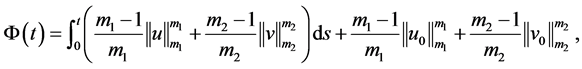 (3.1)
(3.1)
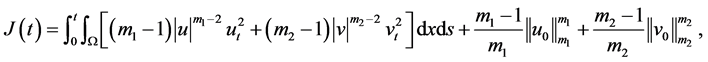 (3.2)
(3.2)
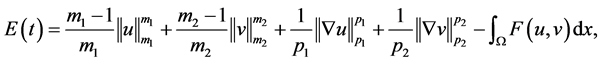 (3.3)
(3.3)
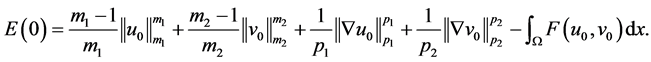 (3.4)
(3.4)
现给出主要引理。
引理3.1. 对任意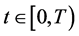 ,下面不等式成立
,下面不等式成立
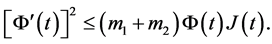 (3.5)
(3.5)
证明 注意到
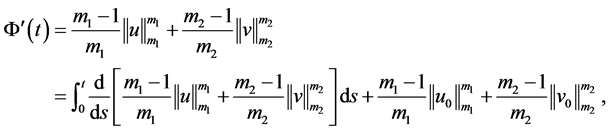 (3.6)
(3.6)
注意到由Holder不等式得下列不等式
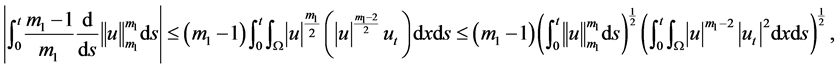 (3.7)
(3.7)
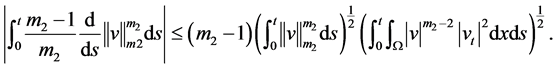 (3.8)
(3.8)
考虑到(3.7)~(3.8),则由(3.6)得
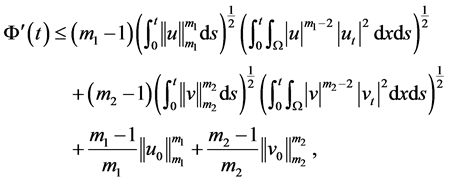
再利用不等式
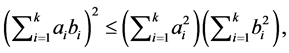
得
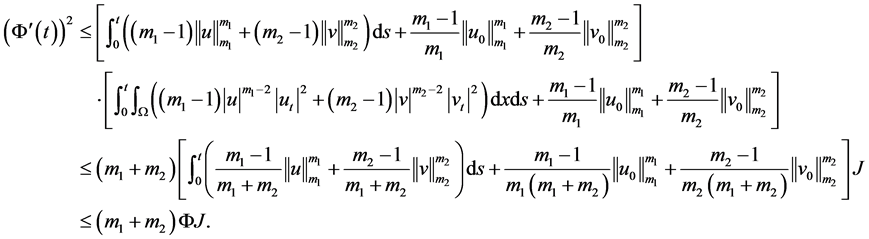
于是,引理得证。
下面,给出主要定理。
定理3.2. 设定理2.1的条件成立,且
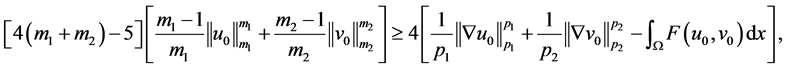 (3.9)
(3.9)
则问题(1.1)~(1.4)的弱解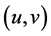 必在某有限时刻
必在某有限时刻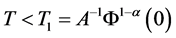 爆破,即
爆破,即
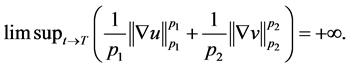
证明 注意到
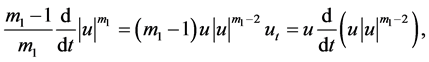
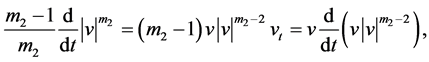
由(3.1),得
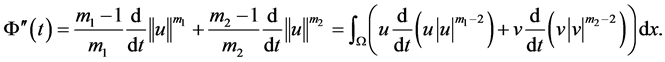
把(1.1),(1.2)代入得
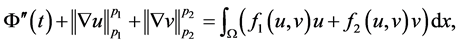 (3.10)
(3.10)
利用
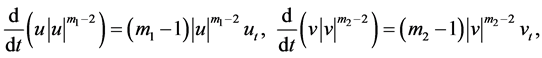
由(3.2)及方程(1.1),(1.2)得
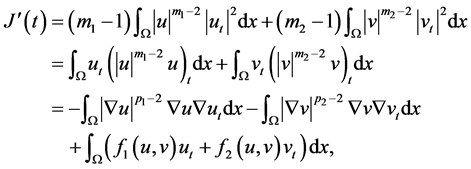
即
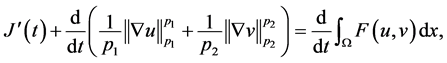 (3.11)
(3.11)
(3.11)关于t积分得
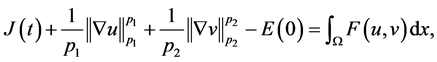 (3.12)
(3.12)
再利用条件(A1)得
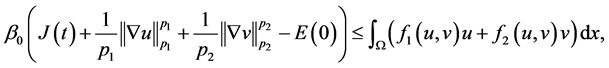 (3.13)
(3.13)
(3.10)结合(3.13),并用到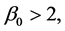 得
得
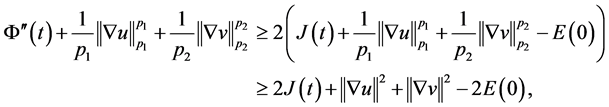
即
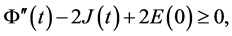 , (3.14)
, (3.14)
注意到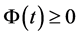 得
得
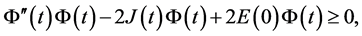 (3.15)
(3.15)
利用引理3.1,得
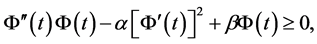
其中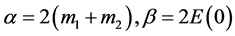 。
。
如果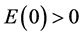 ,由(3.1),(3.6)和(3.9)知
,由(3.1),(3.6)和(3.9)知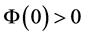 ,
,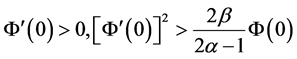 ,于是,由引理2.2得结论。如果
,于是,由引理2.2得结论。如果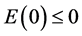 ,取
,取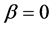 ,则(3.15)变为
,则(3.15)变为
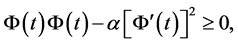 (3.16)
(3.16)
于是,由(3.16)和标准的凸性引理得结论。综合两种情况即得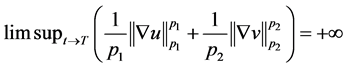 。
。
文章引用
齐龙飞,苏 璟,呼青英, (2015) 多重非线性退化的p-Laplacian抛物方程组解的爆破
Blowup of Solutions for a System of Doubly Nonlinear Degenerate Parabolic Equations with p-Laplacian. 应用数学进展,02,129-135. doi: 10.12677/AAM.2015.42018
参考文献 (References)
- 1. Ball, J.M. (1977) On blowup and nonexistence theorems for nonlinear evolution equations. Quarterly Journal of Ma-thematics: Oxford Journals, 28, 473-486.
- 2. Levine, H.A. (1975) Nonexistence of global weak solutions to some properly and improperly posed problem of mathematical physics: The methods of unbounded Fourier coefficients. Mathematische Annalen, 214, 205-220.
- 3. Bandle, C. and Brumer, H. (1998) Blowup in diffusion equations: A sur-vey. Journal of Computational and Applied Mathematics, 97, 3-22.
- 4. Jiang, Z., Zheng, S. and Song, S. (2004) Blow-up analysis for a nonlinear diffusion equation with nonlinear boundary conditions. Applied Mathematics Letters, 17, 193-199.
- 5. Levine, H.A. (1973) Some nonexistence and instability theorems for solutions of formally parabolic equations of the form . Archive for Rational Mechanics and Analysis, 51, 371-386.
- 6. Lions, J.L. (1969) Quelques methodes de resolution desproblemes aux limites non lineaires. Dunod, Paris.
- 7. Ivanov, A.V. (1993) Quasilinear parabolic equations admitting double degeneracy. St. Petersburg Mathematical Journal, 4, 1153-1168.
- 8. Eden, A., Michaux, B. and Rakotoson, J.M. (1991) Doubly nonlinear parabolic type equations as dy-namical systems. Journal of Dynamics and Differential Equations, 3, 87-131.
- 9. Laptev, G.I. (1997) Solvability of second-order quasilinear parabolic equations with double degeneration. Siberian Mathematical Journal, 38, 1160-1177.
- 10. Tsutsumi, M. (1988) On solution of some doubly nonlinear parabolic equations with absorption. Journal of Mathematical Analysis and Applications, 132, 187-212.
- 11. Eden, A. and Rakotoson, J.M. (1994) Expo-nential attractors for a doubly nonlinear equation. Journal of Mathematical Analysis and Applications, 185, 321-339.
- 12. Miranville, A. (2006) Finite dimensional global attractor for a class of doubly nonlinear parabolic equation. Central European Journal of Mathematics, 4, 163-182.
- 13. Miranville, A. and Zelik, S. (2007) Finite-dimensionality of attractors for degenerate equations of elliptic-parabolic type. Nonlinearity, 20, 1773-1797.
- 14. Hachimi, A.E. and Ouardi, H.E. (2002) Existence and of regularity a global attractor for doubly nonlinear parabolic equations. Electronic Journal of Differential Equations, 2002, 1-15.
- 15. Ouardi, H.E. and Hachimi, A.E. (2006) Attractors for a class of doubly nonlinear parabolic systems. Electronic Journal of Qualitative Theory of Differential Equations, 2006, 1-15.
- 16. Ouardi, H.E. (2007) On the finite dimension of attractors of doubly nonlinear parabolic systems with l-trajectories. Archivum Mathematicum, 43, 289-303.
- 17. Ouardi, H.E. and Hachimi, A.E. (2001) Existence and attractors of solutions for nonlinear parabolic systems. Electronic Journal of Qualitative Theory of Differential Equations, 2001, 1-16.
- 18. Iami, T. and Mochizuki, K. (1991) On the blowup of solutions for quasilinear degenerate parabolic equations. Publications of the Research Institute for Mathematical Sciences, Kyoto University, 27, 695-709.
- 19. Levine, H.A. and Sacks, P.E. (1984) Some existence and nonexistence theorems for solutions of degenerate parabolic equations. Journal of Differential Equations, 52, 135-161.
- 20. Levine, H.A. and Payne, L.E. (1974) Nonexistence theorems for the heat equations with nonlinear boundary conditions and for the porous medium equation backward in time. Journal of Differential Equations, 16, 319-334.
- 21. Levine, H.A., Park, S.R. and Serrin, J.M. (1998) Global existence and nonexistence theorems for quasilinear evolution equations of formally parabolic type. Journal of Differential Equations, 142, 212-229.
- 22. Al’shin, A.B., Korpusov, M.O. and Sveshnikov, A.G. (2011) Blow-up in nonlinear Sobolev type equations. De Gruyter, Berlin/New York.
- 23. Korpusov, M.O. and Sveshnikov, A.G. (2008) Sufficient close-to-necessary conditions for the blowup of solutions to a strongly nonlinear generalized Boussinesq equation. Computational Mathematics and Mathematical Physics, 48, 1591- 1599.
- 24. Polat, N. (2007) Blow up of solution for a nonlinear reaction diffusion equation with multiple nonlinearities. International Journal of Science and Technology, 2, 123-128.
- 25. Wang, J. and Ge, Y.Y. (2012) Blow-up analysis for a doubly nonlinear parabolic system with multi-coupled nonlinearities. Electronic Journal of Qualitative Theory of Differential Equations, 2012, 1-17.
- 26. Agre, K. and Rammaha, M.A. (2006) Systems of nonlinear wave equations with damping and source terms. Differential and Integral Equations, 19, 1235-1270.
- 27. Korpusov, M.O. (2013) Solution blow-up for a class of parabolic equations with double nonlinearity. Sbornik: Mathematics, 204, 323-346.