Advances in Applied Mathematics
Vol.05 No.03(2016), Article ID:18371,9
pages
10.12677/AAM.2016.53048
Bifurcation and Chaos Analysis of a Class of Discrete SIR Epidemic Models
Qin Pang, Jiangang Zhang, Tian Deng, Jun Yin, Jiarong Lu
School of Mathematics, Lanzhou Jiaotong University, Lanzhou Gansu

Received: Jul. 28th, 2016; accepted: Aug. 19th, 2016; published: Aug. 22nd, 2016
Copyright © 2016 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
The paper discusses the dynamical behaviors of a discrete-time SI epidemic model. The local stability of the disease-free equilibrium and endemic equilibrium is obtained. It is shown that the model undergoes Flip bifurcation and Hopf bifurcation by using center manifold theorem and bifurcation theory. So it exhibits the complex dynamical behaviors. These results reveal far richer dynamical behaviors of the discrete epidemic model.
Keywords:Discrete-Time SIR System, Flip Bifurcation, Hopf Bifurcation, Chaos, Random Parameter

一类离散SIR流行病模型的分岔和混沌分析
庞琴,张建刚,邓田,殷俊,卢加荣
兰州交通大学数学学院,甘肃 兰州

收稿日期:2016年7月28日;录用日期:2016年8月19日;发布日期:2016年8月22日

摘 要
本文讨论了离散模型的动力学行为。得到无病平衡点和地方病平衡点的局部稳定性。结果表明,利用中心流形定理和分岔理论,模型存在Flip分岔和Hopf分岔。因此,表现出复杂的动力学行为,这些结果揭示了离散模型的更丰富的动力学行为。
关键词 :离散SIR模型,Flip分岔,Hopf分岔,混沌,随机参数

1. 前言
几个世纪以来,传染病一直以战争和饥荒为主要挑战人类的进步和生存 [1] 。第十四世纪的黑人死亡,1918人的1920次流感疫情至少造成1亿人死亡 [2] 。自1981以来,艾滋病作为一个全球杀手已经威胁到世界的健康,特别是在发展中国家 [3] 。2003年非典的到来对世界有一定影响 [4] 。因此,人们已经进行了许多研究为了更好地了解疾病的发病机制,并进一步控制疾病。研究了利用时间序列模型在 [5] 中的麻疹流行动态。 [6] 和 [7] 中得到的传染病模型的倍周期分岔和混沌。然而,关于随机和混沌性质的儿童疾病,最激烈的讨论发生在上世纪90年代初 [8] 。Nowak和May [9] 中建立数学模型被用来理解现象艾滋病的发病机制,非线性在免疫细胞的病原体和种群之间的相互作用的内在。 [10] 研究了人类免疫缺陷病毒与人体免疫系统相互作用模型中的混沌动力学模型,一般说来,在流行动态模型理论中有2种数学模型:微分方程描述的连续时间模型和差分方程描述的离散时间模型。近年来,对离散时间模型的关注越来越受到关注,已经大量的研究了离散时间模型 [11] - [15] 。在这些文献中,主要的研究方案如下:基本再生数的计算,局部稳定性和全局稳定性的无病平衡的存在,局部稳定性和全局稳定性的地方性平衡。作者讨论了 [16] - [18] 平衡点的稳定性。稳定的振荡已经 [19] [20] 特别是,我们的研究表明,积分步长对离散的非线性动力行为SIR系统积分步长时考虑作为分岔参数。当局部和全局稳定性在离散时间SIR系统。本文的概述如下,在第2部分中,我们给出了离散时间SIR系统。在第3部分中,条件的Flip分岔和Hopf分岔系统(3)是通过利用中心流形定理和分岔理论。
2. 离散的SIR系统
指出每个国家或城市有最大容量治疗一种疾病,Li和wang [21] 。介绍了治疗功能为了描述治疗饱和水平。在 [21] 中研究的模型如下形式:
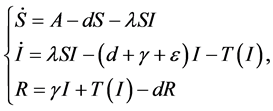 (1)
(1)
其中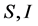 和
和 表示敏感的数量、感染、个人恢复。
表示敏感的数量、感染、个人恢复。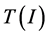 是治疗速度函数,感染的数量低于一个常数固定能力者的人数比例是恒定时感染者数大于能力的人数。对于系统(1),Wang [9] 表明,如果能力是小的,存在一个落后的分支,并存在双稳态特有的平衡,如果能力很低存在阿拉伯学者地方病平衡。类似的模
是治疗速度函数,感染的数量低于一个常数固定能力者的人数比例是恒定时感染者数大于能力的人数。对于系统(1),Wang [9] 表明,如果能力是小的,存在一个落后的分支,并存在双稳态特有的平衡,如果能力很低存在阿拉伯学者地方病平衡。类似的模
型在Zhang和Liu [4] 中作者以饱和处理函数为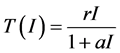 表明,医疗条件是有限的,越来越多的受感
表明,医疗条件是有限的,越来越多的受感
染的个人。在大多数的研究中区划的模型都是由假设总人口是一个常数或满足指数增长 [1] [4] [9] 。更合理的假设给定地区遵循物流增长的人口由于拥挤和有限的资源。流行病模型与物流或广义物流人口结构都进行了广泛的研究( [14] )。然后模型研究采用以下形式:
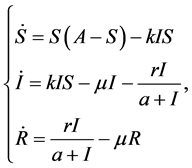 (2)
(2)
其中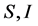 和
和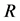 定义如(1).一个是没有疾病的承载能力,和
定义如(1).一个是没有疾病的承载能力,和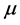 是自然死亡率的人口。
是自然死亡率的人口。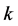 和
和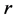 分别感染系数和治愈率,
分别感染系数和治愈率, 存在测量的影响的程度存在延迟治疗感染,所有的参数都是正数。
存在测量的影响的程度存在延迟治疗感染,所有的参数都是正数。
在进入细节之前,我们简化模型。自前两个方程(2)第三个是独立及其动态行为是微小的,当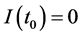 且
且 ,只要考虑前两个方程。因此,我们简化模型:
,只要考虑前两个方程。因此,我们简化模型:
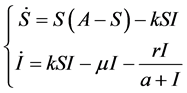 (3)
(3)
应用欧拉离散方法转化系统(3),我们获得以下的离散时间系统
 (4)
(4)
其中 是积分步长
是积分步长
系统的不动点(3)满足下列方程
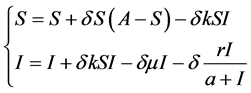 (5)
(5)
正不动点的,我们只需要考虑下列方程的正解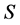 和
和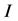 。
。
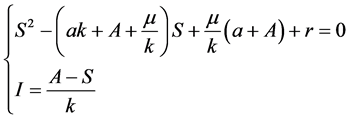 (6)
(6)
因为数量和离散时间系统的不动点的稳定性的相同,为了简单起见,相应的数字和命题不动点的稳定性系统中可以找到
3. 分岔
在本节中,我们主要flip分岔和Hopf分岔系统(3)
3.1. Flip分岔
下面分析Flip分岔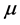 被选为分岔参数。对于不动点
被选为分岔参数。对于不动点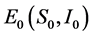 系统的Jacobian矩阵给出了如下:
系统的Jacobian矩阵给出了如下:
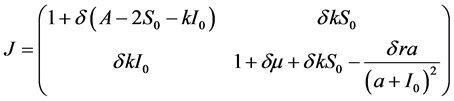 (7)
(7)
Jacobian矩阵的特征方程可以写成
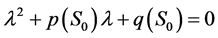 , (8)
, (8)
其中使用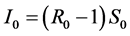 ,
,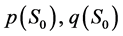 被给出
被给出
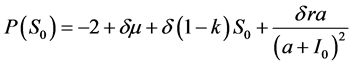
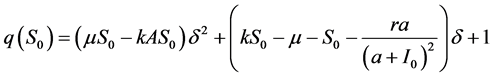 (9)
(9)
 (10)
(10)
由于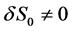 然后不动点
然后不动点 的特征值是
的特征值是
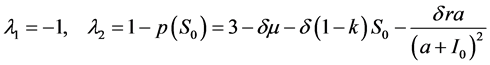 (11)
(11)
让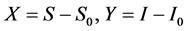 和
和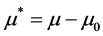 。我们变换不动点
。我们变换不动点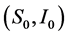 到原点,考虑的参数
到原点,考虑的参数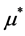 的变量,系统(3)变成
的变量,系统(3)变成
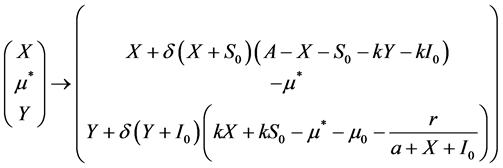 (12)
(12)
之后泰勒展开式对第一和第三个方程的右边,然后映射如下
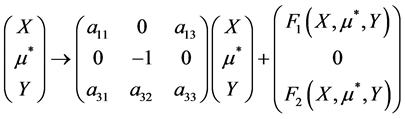 (13)
(13)
其中
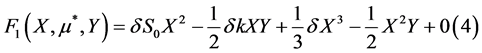
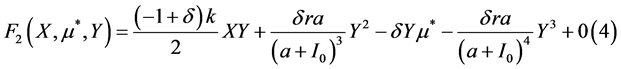 (14)
(14)
其中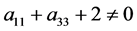 ,我们构建一个可逆矩阵
,我们构建一个可逆矩阵
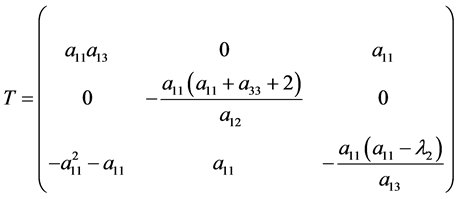
如下变换
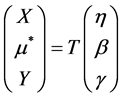 (15)
(15)
映射变成
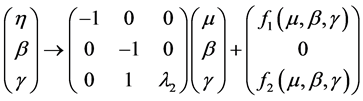 (16)
(16)
其中
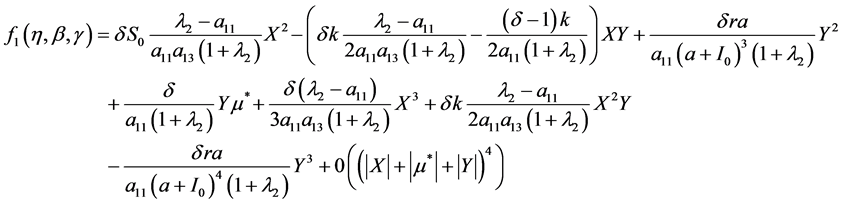
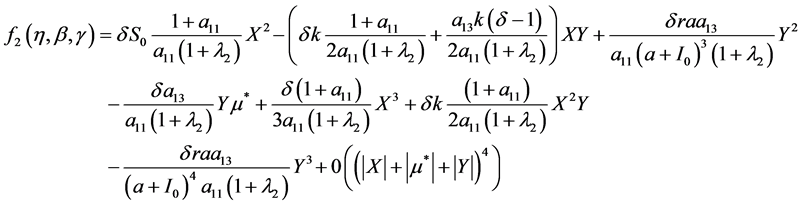 (17)
(17)
通过中心流行理论,稳定性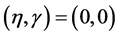 和
和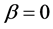 通过研究中心流形上的单参数的映射,可以写成:
通过研究中心流形上的单参数的映射,可以写成:
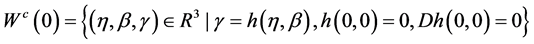
猜想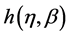 是下列形式
是下列形式
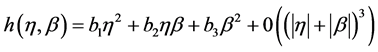 (18)
(18)
比较系数,得
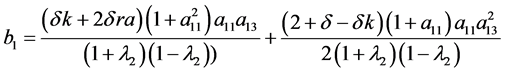
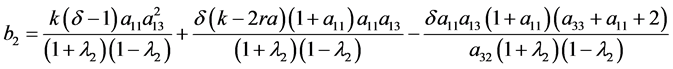 (19)
(19)
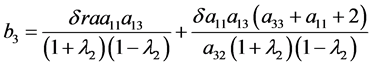
因此,限制映射到的中心流形
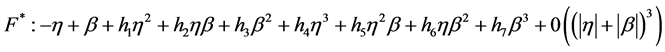 (20)
(20)
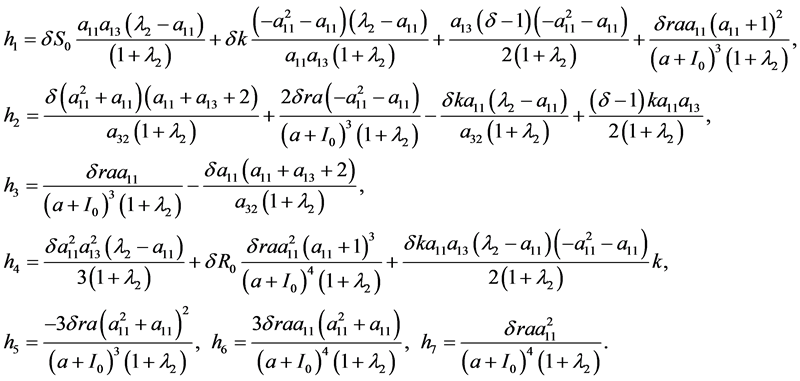 (21)
(21)
如果映射(23)满足Flip分岔,它一定满足下面的条件
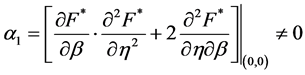 ,
,
和
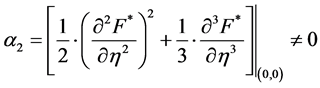
其中
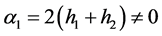
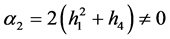 (22)
(22)
其中 和
和 与上面相同,总结以上分析为以下的命题。
与上面相同,总结以上分析为以下的命题。
命题1. 如果条件(10)与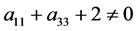 ,
,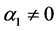 和
和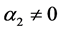 满足,当参数
满足,当参数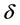 在一个小的领域内变化时,系统(3)在不动点
在一个小的领域内变化时,系统(3)在不动点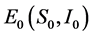 发生Flip分岔,如果
发生Flip分岔,如果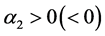 ,那么不动点
,那么不动点 分叉出稳定(不稳定)的2-周期轨。
分叉出稳定(不稳定)的2-周期轨。
3.2. 霍普夫分岔
我们下给霍普夫分岔的生存条件霍普夫分岔用定理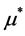 被选作为分岔参数的地方。
被选作为分岔参数的地方。
特征方程的特征值
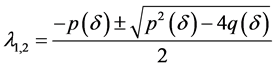 ,
,
其中
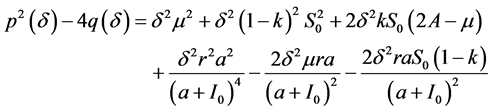 (23)
(23)
特征值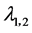 是复数共轭
是复数共轭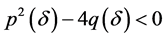 ,其中
,其中
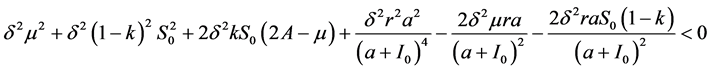 (24)
(24)
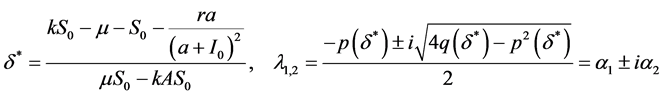 (25)
(25)
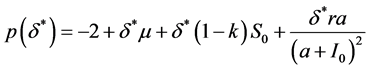 (26)
(26)
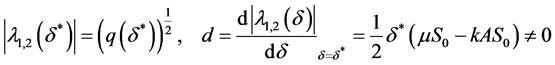 (27)
(27)
此外,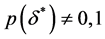 因此
因此
 (28)
(28)
我们得到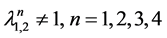 。
。
我们转换稳定点 到原点,变成
到原点,变成 。转换后,映射(3)变成
。转换后,映射(3)变成
 , (29)
, (29)
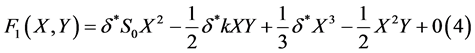
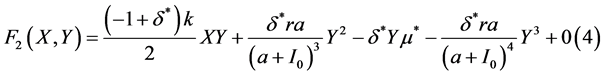 (30)
(30)
让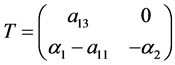 使用变换
使用变换 映射变成
映射变成
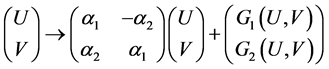 , (31)
, (31)
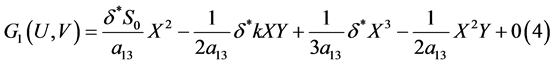
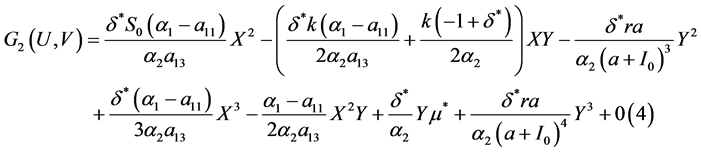 (32)
(32)
接下来,我们计算Hopf分岔的稳定系数的方法。稳定系数给出如下:
 (33)
(33)
其中
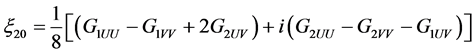 ,
,
 ,
,
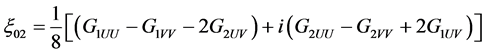 ,
,
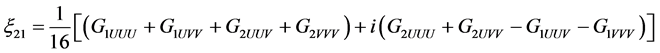 ,(34)
,(34)
其中
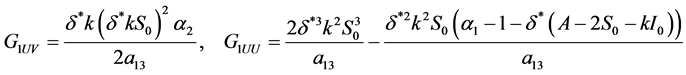
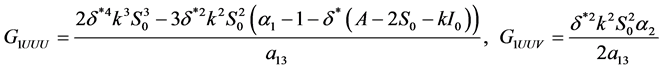
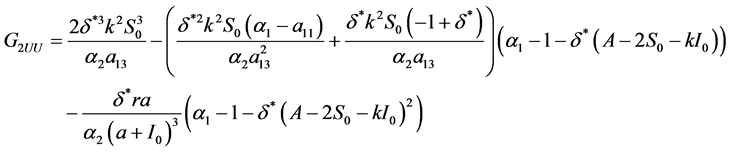
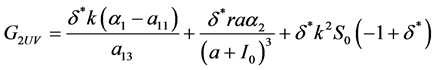
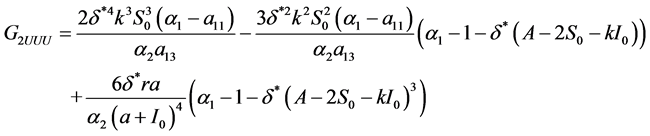
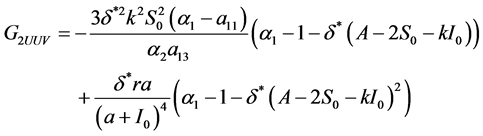
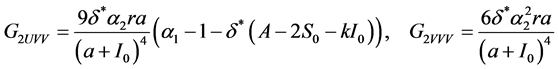 (35)
(35)
命题2. 如果条件(25),(27)和(28)以及(33)需要满足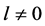 ,当参数
,当参数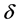 在一个小的领域内变化时,系统(3)在不动点
在一个小的领域内变化时,系统(3)在不动点 发生Hopf分岔,如果
发生Hopf分岔,如果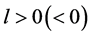 ,那么不动点
,那么不动点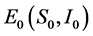 分叉出吸引(排斥)的不变闭曲线。
分叉出吸引(排斥)的不变闭曲线。
4. 结论
在这篇文章中,我们研究Flip分岔、Hopf分岔和混沌对于离散的SIR系统动力学行为。通过使用中心流行理论和分岔理论,已经证明了离散的系统存在Flip分岔和Hopf分岔,以及Filp分岔和Hopf分岔存在条件给出了。然而离散混沌动力学系统仍然需要更深入的研究。在现实世界中,许多传染性疾病表现出季节性波动,如麻疹、百日咳、流行性感冒、水痘、狂犬病(8、9)。基于Hopf分叉时期的研究解决方案,这些结果可能会提供一些新见解的季节性疾病的暴发。在未来,我们还将研究是否时间延迟扩散诱发疾病的季节性断裂结合实际数据。
基金项目
“国家自然科学基金项目”(No 61364001),和甘肃省科学与技术项目(No. 144GKCA018)。
文章引用
庞琴,张建刚,邓田,殷俊,卢加荣. 一类离散SIR流行病模型的分岔和混沌分析
Bifurcation and Chaos Analysis of a Class of Discrete SIR Epidemic Models[J]. 应用数学进展, 2016, 05(03): 390-398. http://dx.doi.org/10.12677/AAM.2016.53048
参考文献 (References)
- 1. Morens, D.M., Folkers, G.K. and Fauci, A.S. (2004) The Challenge of Emerging and Re-Emerging Infectious Diseases. Nature, 430, 242-249. http://dx.doi.org/10.1038/nature02759
- 2. Kohn, G.C. (2004) The Wordsworth Encylo-pedia of Plague and Pestilence. Facts on File, New York, 25-26.
- 3. Johnson, N.P.A.S. and Mueller, J. (2002) Up-dating the Accounts: Global Mortality of the 1918-1920 Spanish Influenza Pandemic. Bulletin of the History of Medicine, 76, 105-115. http://dx.doi.org/10.1353/bhm.2002.0022
- 4. Li, X. and Wang, W. (2005) A Discrete Epidemic Model with Stage Structure. Chaos, Solitons & Fractals, 26, 947- 958. http://dx.doi.org/10.1016/j.chaos.2005.01.063
- 5. Bjørnstad, O.N., Finkenstaedt, B.F. and Greenfell, B.T. (2002) Dynamics of Measles Epidemics: Estimating Scaling of Transmission Rates Using a Time Series SIR Model. Ecological Monographs, 72, 169-184. http://dx.doi.org/10.2307/3100023
- 6. Stone, L., Olinky, R. and Huppert, A. (2007) Seasonal Dynamics of Re-current Epidemics. Nature, 446, 533-536. http://dx.doi.org/10.1038/nature05638
- 7. Aron, J.L. and Schwartz, I.B. (1984) Seasonality and Period-Doubling Bifurcations in an Epidemic Model. Journal of Theoretical Biology, 110, 665-679. http://dx.doi.org/10.1016/S0022-5193(84)80150-2
- 8. Olsen, L.F. and Schaffer, W.M. (1990) Chaos versus Noise Periodicity: Alternative Hypotheses for Childhood Epidemics. Science, 249, 499-504. http://dx.doi.org/10.1126/science.2382131
- 9. Nowak, M. and May, R.M. (1993) AIDS Pathogenesis: Mathe-matical Models of HIV and SIV Infections. AIDS, 7, S3- S18. http://dx.doi.org/10.1097/00002030-199301001-00002
- 10. Lund, O., Mosekilde, E. and Hansen, J. (1993) Period Doubling Route to Chaos in a Model of HIV Infection of the Immune System. Simulation Modelling Practice and Theory, 1, 49-55. http://dx.doi.org/10.1016/0928-4869(93)90015-I
- 11. 崔岩, 刘素华, 葛晓陵. Langford系统Hopf分岔极限环幅值控制. 物理学报, 2012, 61(10): 6-14.
- 12. Chen, X.W., Fu, X.L. and Jing, Z.J. (2013) Complex Dynamics in a Discrete-Time Predator-Prey System without Allee Effect. Acta Mathematicae Applicatae Sinica, 29, 355-376. http://dx.doi.org/10.1007/s10255-013-0221-7
- 13. 刘素华, 赵成刚, 唐驾时, 杨先林. Qi系统的Hopf分分析与幅值控制[J]. 动力学与控制学报, 2008, 6(2): 141-145.
- 14. Ouyang, Q. (2000) Pattern Formation in Reac-tion-Diffusion Systems. Shanghai Sci-Tech Education Publishing House, Shanghai.
- 15. 张美华. Lorenz-84系统的分岔与数值分析[J]. 科学技术与工程, 2010, 10(3): 0743-0746.
- 16. Kuznetsov, Y.A. (1999) Elements of Applied Bi-furcation Theory. 2nd Edition, Springer, New York.
- 17. Wiggins, S. (1990) Introduction to Applied Nonlinear Dy-namical Systems and Chaos. Texts in Applied Mathematics, Vol. 2, Springer, New York. http://dx.doi.org/10.1007/978-1-4757-4067-7
- 18. Hsu, S.B. and Huang, T.W. (1995) Global Stability for a Class of Predator-Prey System. SIAM: SIAM Journal on Applied Mathematics, 55, 763-783. http://dx.doi.org/10.1137/S0036139993253201
- 19. D’Innocenzo, A., Paladini, F. and Renna, L. (2006) A Nu-merical Investigation of Discrete Oscillating Epidemic Models. Physica A, 364, 497-512. http://dx.doi.org/10.1016/j.physa.2005.08.063
- 20. Hassell, M.P., Comins, H.N. and May, R.M. (1991) Spatial Structure and Chaos in Insect Population Dynamics. Nature, 353, 255-258. http://dx.doi.org/10.1038/353255a0
- 21. Engbert, R. and Drepper, F.R. (1994) Chance and Chaos in Population Biology—Models of Recurrent Epidemics and Food Chain Dynamics. Chaos, Solitons & Fractals, 4, 1147-1169. http://dx.doi.org/10.1016/0960-0779(94)90028-0