Advances in Applied Mathematics
Vol.06 No.01(2017), Article ID:19632,9
pages
10.12677/AAM.2017.61009
Heterogeneous Complex Number and Heterogeneous Complex Function
Xuejiao Zhao1, Yun Chen2, Jicheng Tao2
1College of Liangxin, China Jiliang University, Hangzhou Zhejiang
2Department of Mathematics, China Jiliang University, Hangzhou Zhejiang

Received: Jan. 4th, 2017; accepted: Jan. 21st, 2017; published: Jan. 24th, 2017
Copyright © 2017 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
In this paper, we introduce the definitions of heterogeneous complex number and heterogeneous complex function, and then discuss the property of heterogeneous complex function. We establish the relationship between heterogeneous complex analytic function and partial differential equation system.
Keywords:Heterogeneous Complex Number, Heterogeneous Complex Analytic Function, Heterogeneous C.R. Partial Differential Equation System

非均匀复数与非均匀复变函数
赵雪娇1,陈雲2,陶继成2
1中国计量大学,量新学院,浙江 杭州
2中国计量大学,应用数学系,浙江 杭州

收稿日期:2017年1月4日;录用日期:2017年1月21日;发布日期:2017年1月24日

摘 要
本文给出了非均匀复数的定义,非均匀复解析函数的定义和性质,建立了非均匀复解析函数与偏微分方程的关系。
关键词 :非均匀复数,非均匀复解析函数,非均匀C.R.方程组

1. 引言
在文献 [1] [2] [3] 中,作者们介绍了生物学的一些反应扩散模型,讨论的问题是借助于均匀底空间的非均匀流形的扩散性,对于这些非均匀性的问题,长期以来都是采取均匀底空间上讨论非均匀的丛空间,这样给问题的研究带来很多麻烦。
本文从最基本问题探讨,我们知道,瑞士数学家欧拉在1777系统地建立了复数理论,发现了复指数函数和三角函数间的关系,创立了复变函数论的一些基本定理,并开始把它们用到水力学和地图制图学上,用符号i作为虚数的单位,建立了复变函数理论,随后发现复数与调和函数有密切的联系 [4] [5] [6] ,在文献 [7] [8] 建立了广义解析函数理论,这些问题自然与扩散问题也有紧密联系,从而可以用复变函数理论解扩散问题的解,但当空间非常不均匀,扩散也不均匀时,解决问题会非常繁琐,鉴于上述问题,本文试图推广复数的定义到广义复数,具体就是对虚数单位一般化,定义j为虚数单位,但它的模不是1,这样保证在变化过程中不均匀变化,为了更突出我的问题的实际意义又不与文献 [7] [8] 概念混淆,我们把这种广义的复数称为非均匀复数,它上的函数称为非均匀复变函数。
2. 非均匀复数的定义及性质
2.1. 非均匀复数的定义
考虑到复数在各个领域的广泛应用,我们对复数单位做进一步推广,定义非均匀复数。
定义集合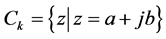 ,其中,
,其中,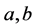 为实数
为实数 ,
, 。
。
在 中引入数乘
中引入数乘

在 中引入加法
中引入加法
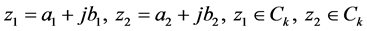
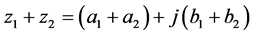
定理2.1 在上式数乘和加法运算下, 为
为 上的一个线性空间。
上的一个线性空间。
证:
因为 ,所以
,所以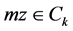
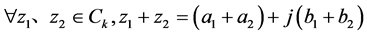
因为 ,所以
,所以
即证明 为
为 上的一个线性空间。
上的一个线性空间。
在 中引入乘法
中引入乘法
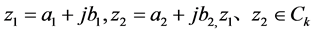

定理2.2 为
为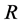 上的一个域。
上的一个域。
证: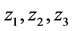 为
为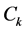 中任意元素,
中任意元素, 为
为 中任意非零元素,
中任意非零元素,
 。
。 上的加法运算构成加群
上的加法运算构成加群
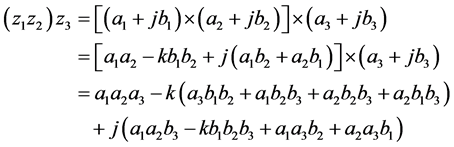

可以看出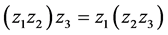 ,即
,即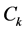 对加法满足结合律。
对加法满足结合律。
 ,
,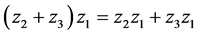 ,
,
即 中乘法对加法满足左右分配律则称
中乘法对加法满足左右分配律则称 对这两个代数运算作成一个环。
对这两个代数运算作成一个环。
易知 ,且
,且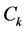 有单位元1,对于
有单位元1,对于 中任意的非零元素
中任意的非零元素 ,其共轭为
,其共轭为 ,定义
,定义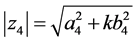 ,可得
,可得 的逆元
的逆元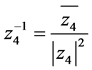 ,则知每个非零元都有逆元,得出
,则知每个非零元都有逆元,得出 为一个除环,又因
为一个除环,又因 ,所以
,所以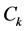 为一个可换除环,称为域。
为一个可换除环,称为域。
定义2.1 满足定理2.1、2.2的 称为非均匀复数。
称为非均匀复数。
3. 非均匀复变函数定义及性质
3.1. 非均匀复变函数的概念
非均匀复变函数的定义,类似于复变函数的定义,形式上和数学分析中函数定义相同,此时自变量和函数的取值均为新定义的非均匀复数.在定义函数之前,根据复平面点集的几个基本概念,我们可以推广到广义复平面上。
定义3.1 由不等式 所确定的平面点集(简称点集),就是以
所确定的平面点集(简称点集),就是以 为圆心,以
为圆心,以 为半径的圆,称为点
为半径的圆,称为点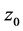 的
的 邻域。
邻域。
注3.1:考虑点集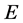 ,同样也有聚点或极限点、孤立点、外点、闭集、内点、开集、边界点、边界的概念,与复变平面定义相同,在此不再一一赘述。
,同样也有聚点或极限点、孤立点、外点、闭集、内点、开集、边界点、边界的概念,与复变平面定义相同,在此不再一一赘述。
定义3.2设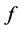 :从
:从 到
到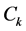 的映射,则称为
的映射,则称为 为
为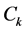 上的非均匀复函数。
上的非均匀复函数。
3.2. 非均匀复变函数的极限和连续性
定义3.3 设函数 于点集
于点集 上有定义,
上有定义,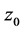 为
为 的聚点如存在非均匀复数
的聚点如存在非均匀复数 ,对任给的
,对任给的 ,有
,有 ,只要
,只要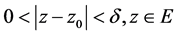 ,就有
,就有

则称函数 沿
沿 于
于 有极限
有极限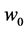 ,并记为
,并记为
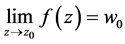
定义3.4 设函数 在点集
在点集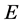 上有定义,
上有定义,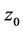 为 的聚点,且
为 的聚点,且 ,若
,若
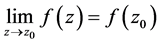
即对任给的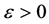 ,有
,有 ,只要
,只要 ,就有
,就有

则称 沿
沿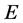 于
于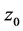 连续。
连续。
如函数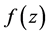 在点集
在点集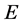 上各点均连续,则称
上各点均连续,则称 在
在 上连续。
上连续。
3.3. 非均匀复变函数的导数
定义3.5 设函数 在点
在点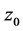 的领域内或包含
的领域内或包含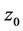 的区域
的区域 内有定义,考虑比值
内有定义,考虑比值

如果当 按照任意方式趋于
按照任意方式趋于 时,即当
时,即当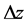 按照任意方式趋于0时,比值
按照任意方式趋于0时,比值 的极限都存在,且其值有限,则称此极限为函数
的极限都存在,且其值有限,则称此极限为函数 在
在 的导数,并记为
的导数,并记为 即
即

这时称函数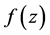 于点
于点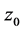 可导。
可导。
设函数 在点z可导,于是
在点z可导,于是
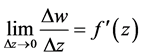
即是
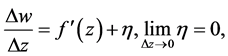
 ,
,
其中 为比
为比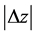 高阶的无穷小。
高阶的无穷小。
称 为
为 在点
在点 的微分,记为
的微分,记为 或
或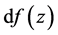 ,此时也称
,此时也称 在点
在点 可微,即
可微,即

特别,当 时,
时,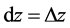 ,于是上式为
,于是上式为 ,即
,即

由此可见: 在
在 处可导与
处可导与 在
在 处可微是等价的。
处可微是等价的。
3.4. 非均匀复变函数的解析性
定义3.6 如果函数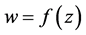 在区域
在区域 内可微,则称
内可微,则称 为区域
为区域 内的解析函数,或称函数
内的解析函数,或称函数 在区域
在区域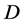 内解析。函数在某点解析,是指在该点的某一个邻域内是解析的;函数在某个闭域解析,是指在包含该闭域的某区域内解析。
内解析。函数在某点解析,是指在该点的某一个邻域内是解析的;函数在某个闭域解析,是指在包含该闭域的某区域内解析。
3.5. 非均匀复变函数的解析性与偏微分方程的关系
为了描述非均匀复变函数的解析性与偏微分方程的关系,不妨假设

是非均匀复变元 的一个定义在区域
的一个定义在区域 内的函数,当二元实数
内的函数,当二元实数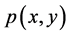 及
及 给定时,此函数也就完全确定。
给定时,此函数也就完全确定。
我们假设函数 是可微的,那么其实部
是可微的,那么其实部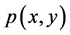 与虚部
与虚部 应当不是相互独立的,这是必须满足一定的条件的仿照柯西-黎曼方程(简称C.-R.方程)的探讨方法。
应当不是相互独立的,这是必须满足一定的条件的仿照柯西-黎曼方程(简称C.-R.方程)的探讨方法。
若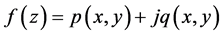 在某一点
在某一点 可微,而且设
可微,而且设

又设 ,其中
,其中
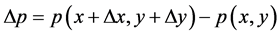

于是 变为
变为

 无论是按什么方式趋于零时,
无论是按什么方式趋于零时, 总是成立的,先设
总是成立的,先设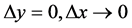 ,即变点
,即变点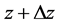 沿平行于实轴的方向趋于点
沿平行于实轴的方向趋于点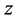 ,此时
,此时 变成
变成

于是可知 必然存在,且有
必然存在,且有
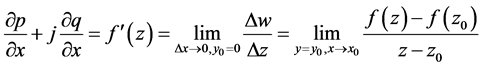
同样,设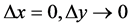 ,即变点
,即变点 沿平行于虚轴的方向趋于点
沿平行于虚轴的方向趋于点 ,此时成为
,此时成为
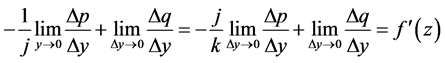
于是可知 必然存在,且有
必然存在,且有
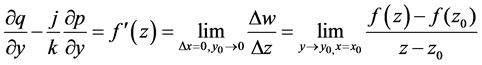
由上面两式子得出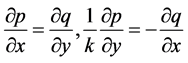 ,
,
这是类似于柯西-黎曼方程的关于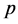 及
及 的偏微分方程,我们称为非均匀柯西-黎曼方程(简称广义C.-R.)根据以上讨论,我们获得如下结论:
的偏微分方程,我们称为非均匀柯西-黎曼方程(简称广义C.-R.)根据以上讨论,我们获得如下结论:
定理3.1设函数 在区域
在区域 内有定义,且在
内有定义,且在 内一点
内一点 可微,则必有
可微,则必有
偏微分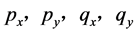 在点
在点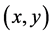 存在;
存在; 在点
在点 满足广义C.-R.方程。
满足广义C.-R.方程。
而且这是可微的必要条件,并非充分的。
定理3.2设函数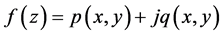 在区域
在区域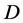 内有定义,且在
内有定义,且在 内一点
内一点 可微,则必有
可微,则必有
(1) 偏微分 在点
在点 可微;
可微;
(2) 在点
在点 满足广义C.-R.方程。
满足广义C.-R.方程。
这是可微的充要条件。
证明:根据上述非均匀柯西-黎曼方程可知,当条件(1) (2)满足时, 在点
在点 的导数可以表示为
的导数可以表示为
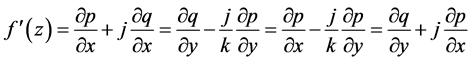
(必要性)设 在
在 内一点 可微,则
内一点 可微,则

其中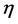 是随
是随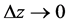 而趋于零的复数,若令
而趋于零的复数,若令

则

这里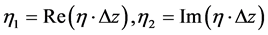 是
是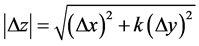 的高阶无穷小。
的高阶无穷小。
比较上式两段的实、虚部,即得


由数学分析中二元函数的微分定义即知, 与
与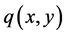 在点
在点 可微,且
可微,且

(充分性)由 与
与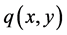 的可微性可知,在
的可微性可知,在 中有
中有


其中 是
是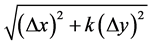 的高阶无穷小。
的高阶无穷小。
再由广义C.-R.方程,可设

于是就有

或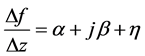
其中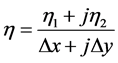 随
随 而趋于零。因为
而趋于零。因为

所以
即
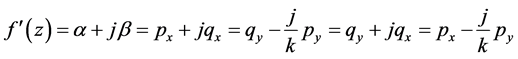
定理3.3设函数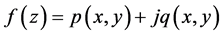 在区域
在区域 内有定义,且在
内有定义,且在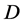 内一点
内一点 可微,则必有
可微,则必有
(1) 偏微分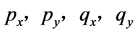 在点
在点 连续;
连续;
(2)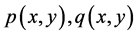 在点
在点 满足非均匀C.-R.方程。
满足非均匀C.-R.方程。
这是可微的充分条件。
定理3.4设函数 在区域
在区域 内解析,则
内解析,则
(1) 二元函数 在区域
在区域 内可微;
内可微;
(2) 在
在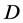 内满足非均匀C.-R.方程。
内满足非均匀C.-R.方程。
定理3.5设函数 在区域
在区域 内解析,则
内解析,则
(1) 偏微分 在
在 内连续;
内连续;
(2) 在
在 内满足非均匀C.-R.方程。
内满足非均匀C.-R.方程。
定理3.4和3.5都是函数解析的充要条件。
3.6. 一些基本解析函数
例3.1:证明函数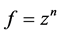 可导。
可导。
证明:(1) 时,
时,

(2) 时,
时,

(n) 时,
时,
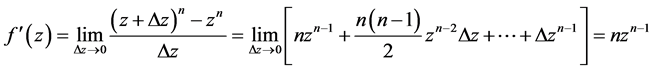
例3.2:考虑函数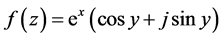 在
在 平面上的解析性。
平面上的解析性。
不妨令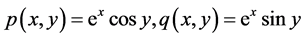 ,
,
根据定义
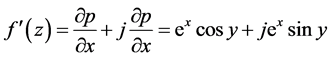
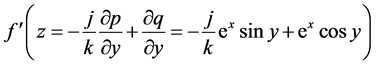
从而有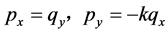 ,在
,在 平面上处处连续,且满足非均匀C.-R.方程。
平面上处处连续,且满足非均匀C.-R.方程。
由定理3.5可知,
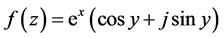 在
在 平面上是解析的。
平面上是解析的。
4. 初等解析函数
4.1. 非均匀指数函数
由例3.2我们知道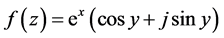 在
在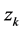 平面上是解析的,且有
平面上是解析的,且有 ,
,
因此我们自然可以给出下面的定义:
定义4.1 对于任何非均匀复数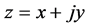 ,我们定义下面的函数为非均匀指数函数:
,我们定义下面的函数为非均匀指数函数:
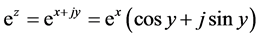
对于非均匀指数函数,易得下面的一些性质:
如 ,我们定义与实指数函数的定义一致;
,我们定义与实指数函数的定义一致;
 在
在 平面上市解析的
平面上市解析的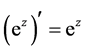 ;
;
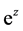 是以
是以 为基本周期的周期函数;
为基本周期的周期函数;
如果 ,我们有:
,我们有:

4.2. 非均匀三角函数
由 ,得
,得 ,由于前面两公式中的
,由于前面两公式中的 以任意非均匀复数取代左边有意义,因此我们给出非均匀三角函数的定义:
以任意非均匀复数取代左边有意义,因此我们给出非均匀三角函数的定义:
定义4.2定义
 ,分别称为
,分别称为 的正弦和余弦函数。
的正弦和余弦函数。
5. 非均匀解析函数与非均匀拉普拉斯方程的关系
设 为非均匀解析函数,其中
为非均匀解析函数,其中 ,假设
,假设 是
是 有两阶连续偏导数的实函数,在这些假设中,我们获得如下定理:
有两阶连续偏导数的实函数,在这些假设中,我们获得如下定理:
定理5.1设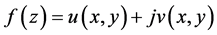 为非均匀解析函数,其中
为非均匀解析函数,其中 ,假设
,假设 是
是 有两阶连续偏导数的实函数,则有
有两阶连续偏导数的实函数,则有 。
。
证明:因为 为非均匀解析函数,有非均匀C.R.条件:
为非均匀解析函数,有非均匀C.R.条件:

两边对 求偏导,再利用
求偏导,再利用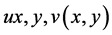 是
是 有两阶连续偏导数的实函数,就可以获得:
有两阶连续偏导数的实函数,就可以获得:
 。
。
注5.2:在经典的复变函数理论中,若有 是解析的,利用Cauchy积分理论,可以得到
是解析的,利用Cauchy积分理论,可以得到 的任意阶导数,从而我们就可以自然获得
的任意阶导数,从而我们就可以自然获得 是
是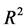 有两阶连续偏导数的实函数,但是我们由于篇
有两阶连续偏导数的实函数,但是我们由于篇
幅所限,积分理论这一部分在我们准备完成的后续论文中,且我们把方程 称为非均匀拉
称为非均匀拉
普拉斯方程,我们可以预见,定理5.1是一个充分必要条件。
6. 结论
本文给出了非均匀复数和非均匀解析函数的定义,建立了非均匀解析函数与偏微分方程的关系。还有很多进一步讨论的内容,如何建立非均匀复函数的积分理论,是否有Cauchy积分公式和积分定理;偏微分方程与非均匀解析函数的关系,类似的留数定理;以及在物理,力学的应用。
基金项目
中国计量大学第十九届学生科研计划项目资助。浙江省自然科学基金资助,项目编号:LY16A010009。
文章引用
赵雪娇,陈雲,陶继成. 非均匀复数与非均匀复变函数
Heterogeneous Complex Number and Heterogeneous Complex Function[J]. 应用数学进展, 2017, 06(01): 69-77. http://dx.doi.org/10.12677/AAM.2017.61009
参考文献 (References)
- 1. 楼元. 空间生态学中的一些反应扩散方程模型[J]. 中国科学: 数学, 2015, 45(10): 1619-1634.
- 2. Allen, L., Bolker, B., Lou, Y., et al. (2007) Asymptotic Profile of the Steady States for an SIS Epidemic Patch Model. SIAM Journal on Applied Mathematics, 67, 1283-1309. https://doi.org/10.1137/060672522
- 3. Wang, W. and Zhao, X.Q. (2011) A Nonlocal and Time-Delayed Reac-tion-Diffusion Model of Dengue Transmission. SIAM Journal on Applied Mathematics, 71, 147-169. https://doi.org/10.1137/090775890
- 4. 李忠. 复分析导引[M]. 北京: 北京大学出版社, 2004.
- 5. 钟玉泉. 复变函数论[M]. 北京: 高等教育出版社, 2012.
- 6. 钟玉泉. 解析函数的单叶半径[J]. 四川大学学报(自然科学版), 1991, 28(4): 545-547
- 7. 胡庆平. 广义复变函数论(I) [J]. 西北大学学报(自然科学版), 1984(2): 117-119.
- 8. 濮德潜. 广义复数上的函数[J]. 纯粹数学与应用数学, 1991(2): 69-79.