求解区间参数非线性方程组的数值方法 Numerical Method for Solving Nonlinear Equations with Interval Parameter

doi:10.12677/AAM.2017.67105

Advances in Applied Mathematics
Vol.06 No.07(2017), Article ID:22546,10 pages
10.12677/AAM.2017.67105

Numerical Method for Solving Nonlinear Equations with Interval Parameter

Qi Wang, Wang Xiao, Haijun Wang^*

●Abstract

●Full-Text PDF

●Full-Text HTML

●Full-Text ePUB

●Linked References

●How to Cite this Article

School of Mathematics, China University of Mining and Technology, Xuzhou Jiangsu

Received: Oct. 8^th, 2017; accepted: Oct. 24^th, 2017; published: Oct. 31^st, 2017

ABSTRACT

In this paper, the problem of solving nonlinear equations with interval parameters is considered. By improving interval Krawczyk operator and applying Newton order-reduction method, we propose an interval algorithm to solve nonlinear equations with interval parameters. The theoretical result and numerical test are given and numerical result shows that proposed interval algorithm can effectively solve nonlinear equations with interval parameters.

Keywords:Nonlinear Equations with Interval Parameters, Newton Order-Reduction Method, Krawczyk Operator

求解区间参数非线性方程组的数值方法

王琪，肖旺，王海军^*

中国矿业大学数学学院，江苏徐州

收稿日期：2017年10月8日；录用日期：2017年10月24日；发布日期：2017年10月31日

摘要

本文研究了区间参数非线性方程组的求解问题，通过改进区间Krawczyk算子并结合牛顿降阶法提出了求解区间参数非线性方程组的区间算法，给出了相关的理论结果和数值有效性测试。数值算例表明提出的算法可以有效的求解区间参数非线性方程组。

关键词 :区间参数非线性方程组，牛顿降阶法，Krawczyk算子

This work is licensed under the Creative Commons Attribution International License (CC BY).

http://creativecommons.org/licenses/by/4.0/

1. 引言

非线性方程组在数学、经济、工程等领域有着广泛的应用，如机器人学中的几何设计问题 [1] 、化学工程中的分子模型问题 [2] ，动力学中的平衡问题 [3] 等。因此，求解非线性方程组是一项十分重要而且有意义的工作。但是在实际问题中经常会使用到游标卡尺、螺旋测微仪、分析天平等精度较高的仪器，难免会出现测量误差，再加上浮点运算也会出现误差，那么经过传统的非线性方程组求得的这些问题的结果可能会失去意义。为了得到可靠的计算结果，可以用区间来包含这些带有误差的测量数据。因此，在实际计算中，我们常常需要解决含不定参数的非线性方程组：

$f (x, [p]) = 0,$ (1)

这里 $f = {(f_{1}, \dots, f_{n})}^{T}$ ， $x = {(x_{1}, \dots, x_{n})}^{T}$ ， $f_{i} : R^{n} \times I R \to I R$ ， $[p] \in I R$ ， $I R$ 表示所有实区间集合。我们称(1)为区间参数非线性方程组，为了方便起见，我们将区间参数非线性方程组表示成以下形式：

$f (x) = 0,$ (2)

这里 $f : R^{n} \times I R \to R^{n}, x \in R^{n}$ 。

区间参数非线性方程组的解集定义为：

$\sum = {x \in R^{n} : \exists f (x) \in f (x) s . t . f (x) = 0} .$

显然，区间参数非线性方程组解的情况有三种：无解、有限个解和无穷多解。因为(2)的系数是不断变化的，所以它的解也是不断变化的。但是，(2)的解是由所有非线性方程组 $f (x) \in f (x)$ 的解构成的。当(2)有无穷多解时，这些解通常会构成一个封闭的区域。我们的目的是获取解集 $Σ$ 的区间包，即求解尽可能小的区间 $[x]$ 使得 $Σ \subseteq [x]$ 。

1966年Moore在 [4] 《Interval Analysis》一书中第一次用区间Newton法逼近了一个简单的区间方程的零解；1969年Krawczyk [5] 针对Moore的区间Newton程序在计算量方面的缺陷(求区间矩阵的逆计算量比较大)提出了区间Krawczyk算子；1992年Hansen [6] 利用牛顿法提出了区间搜索和启发式的终止条件求解区间方程的零解；2006年Nikas [7] 等在理论上提出了一种边界近似的方法求解区间方程，并取得了很好的成果；2009年Nikas [8] 等又基于牛顿法提出了通过分离零解区间端点的方法求解区间方程。2017年邱亮 [9] 等基于单调分割技术拓展了Nikas的方法，在计算效率上有所提高。

本文基于区间Krawczyk算子，将区间Krawczyk算子推广到求解区间参数非线性方程组，并结合区间Newton降阶法得到改进的区间Krawczyk算子。第二部分介绍了区间Krawczyk算子与区间扩展；第三部分改进了区间Krawczyk算子并证明了改进的区间Krawczyk算子及其分量形式在指定初始区间内解的存在性；第四部分利用改进的区间Krawczyk算子和区间Newton降阶法设计了求解区间参数非线性方程组的算法；第五部分给出了数值算例，证明该算法的可行性与有效性。

2. 区间Krawczyk算子与区间扩展

1996年Moore [4] 基于点Newton法提出了区间Newton法，对于非区间方程组 $f (x) = 0$ ， $x \in [x] \subseteq I R$ ， $x^{*}$ 是方程的解，且 $x^{*} \subseteq [x]$ ，则传统的区间牛顿法公式为：

$N ([x]) = : m - \frac{F (x)}{F^{'} ([x])},$

其中：m是 $[x]$ 内的任意一点(通常取m为 $[x]$ 的中点)，F和 $F^{'}$ 是f和 $f^{'}$ 在区间 $[x]$ 上的区间扩展函数。

1969年Krawczyk [5] 推广了Moore的区间Newton法得到了区间Krawczyk算子，

$K ([x]) = : m - Y f (m) + (I - Y F^{'} ([x])) ([x] - m)$

其中：m是 $[x]$ 内的任意一点(通常取m为 $[x]$ 的中点)， $F^{'}$ 是 $f^{'}$ 在区间 $[x]$ 上的区间扩展函数，Y为任意非奇异矩阵。

对于向量函数 $f : R^{n} \to R^{n}$ ，目前存在着很多求解函数区间包含的区间方法，这些方法被应用到很多领域 [10] [11] [12] [13] 。由于向量函数 $f : R^{n} \to R^{n}$ 的区间扩展相当于对每一个分量 $f_{i} (x) (i = 1, \dots, n)$ 进行区间扩展，因此我们只简短的介绍函数 $f : R^{n} \to R$ 的区间扩展。最常见的区间扩展方法有自然扩展、中值扩展，具体形式如下：

自然扩展： $F_{N} ([x]) = F ([x]),$

中值扩展： $F_{M} ([x], c) = f (c) + F ([x]) ([x] - c),$

这里 $c \in [x], F^{'} ([x]) = {({F^{'}}_{1} ([x]), \dots, {F^{'}}_{n} ([x]))}^{T}$ ， ${F^{'}}_{j} ([x])$ 是 $\frac{\partial f (x)}{\partial x_{j}}$ 在区间 $[x]$ 上的区间扩展， $F ([x])$ 是用区间 $[x]$ 代替点变量x求解函数值所得。

对于中值扩展 $F_{M} ([x], c)$ ，Baumann [14] 对c的每一个分量进行特殊的选择，使得中值扩展更接近于函数 $f (x)$ 在区间 $[x]$ 上的值域，具体如下：

设 $F^{'} ([x]) = [\underline{l}, \bar{l}], i = 1, 2, \dots, n$ ，点向量 $\underline{c}$ 与 $\bar{c}$ 定义为：

${\underline{c}}_{i} = {\begin{cases} {\bar{x}}_{i}, {\bar{l}}_{i} \leq 0, \\ {\underline{x}}_{i}, {\underline{l}}_{i} \geq 0, \\ ({\bar{l}}_{i} {\underline{x}}_{i} - {\underline{l}}_{i} {\bar{x}}_{i}) / ({\bar{l}}_{i} - {\underline{l}}_{i}), 其他情形, \end{cases}$ (3)

${\underline{c}}_{i} = {\begin{cases} {\underline{x}}_{i}, {\bar{l}}_{i} \leq 0, \\ {\bar{x}}_{i}, {\underline{l}}_{i} \geq 0, \\ ({\underline{l}}_{i} {\underline{x}}_{i} - {\bar{l}}_{i} {\bar{x}}_{i}) / ({\underline{l}}_{i} - {\bar{l}}_{i}), 其他情形, \end{cases}$ (4)

则对于任意的 $c \in [x]$ ，有

$\inf F_{M} ([x], c) \leq \inf F_{M} ([x], \underline{c}), \sup F_{M} ([x], \bar{c}) \leq \sup F_{M} ([x], c) .$

我们称最优中心形式为：

$\begin{matrix} F_{o} ([x], \bar{c}, \underline{c}) = [\inf F_{M} ([x], \underline{c}), \sup F_{M} ([x], \bar{c})] \\ = [\inf {f (\underline{c}) + F^{'} ([x]) ([x] - \underline{c})}, \sup {f (\bar{c}) + F^{'} ([x]) ([x] - \bar{c})}] . \end{matrix}$

很显然

${f (x) : x \in [x]} \subseteq F_{o} ([x], \bar{c}, \underline{c}) \subseteq F_{M} ([x], c),$ (5)

即最优中心形式改善了中值扩展的效率。Wang-Cao [15] 证明在某些情况下，中值扩展的最优中心形式效率要高于自然扩展。

引理1 [15] ：假设函数 $f : D \subset R^{n} \to R$ 连续可微且 $F^{'} ([x])$ 为函数 $f (x)$ 的具有包含单调性的区间扩展。如果 $0 \in F^{'} ([x])$ 且 $ω (F_{N} ([x])) \leq α \cdot ω ([x])$ ，则

$F_{N} ([x]) \subseteq F_{o} ([x], \bar{c}, \underline{c}),$

这里c是由(3)和(4)定义的， $α > 0$ 为一常数。

例1：对于函数 $f (x)$ ，我们考虑用区间扩展求解其值域的区间包含，结果见表1。

$f (x) = {\begin{cases} x_{1}^{3} + [0.9, 1.1] x_{2}^{2} - 5, \\ (x_{1} + 1) x_{2} - (3 x_{1} + [0.9, 1.1]) . \end{cases}$

从表中可以明显看出，利用区间扩展方法求解值域的区间包含， $F_{N} ([x]) \cap F_{o} ([x], \underline{c}, \bar{c})$ 是一种较好的选择。

3. 改进的区间Krawczyk算子

区间参数非线性方程组(2)等价于

$x = p (x) = x - C f (x),$

其中c为非奇异点矩阵，通常取 $C = {m (F^{'} ([x]))}^{- 1}$ 。

定义1：对任意区间向量 $[x] \in I R^{n}$ ，点向量 $c \in [x]$ ，非奇异矩阵 $C \in R^{n \times n}$ ， $F^{'} ([x])$ 为区间函数 $f (x)$ 导数的区间扩展，区间映射

$K ([x], c) = c - C f (c) + (I - C F^{'} ([x])) ([x] - c)$

称为改进的区间Krawczyk算子，c通常取区间向量 $[x]$ 的中点。

定理1：假设区间参数非线性函数 $f : D \subset R^{n} \to R^{n}$ 连续可微， $x^{*}$ 为区间参数非线性方程组(2)的任意实数解。则

1) 如果 $x^{*} \in [x]$ ，则 $x^{*} \in K ([x], c)$ ；

2) 如果 $K ([x], c) \cap [x] = \emptyset$ ，则区间 $[x]$ 不含有区间参数非线性方程组(2)的任何解；

3) 如果 $K ([x], c) \subseteq [x]$ ，则 $[x]$ 一定包含区间参数非线性方程组(2)的一个解。

证明：

Table 1. The comparison for effectiveness of interval extension

表1. 区间扩展有效性比较

1) 由于 $x^{*}$ 为区间参数非线性方程组(2)的一个解，则存在 $f (x) \in f (x)$ 使得 $f (x) \in f (x)$ ，故

$\begin{matrix} x^{*} = x^{*} - C f (x^{*}) = c - C f (c) + x^{*} - c - C (f (x^{*}) - f (c)) \\ = c - C f (c) + x^{*} - c - C f^{'} (c + θ (x^{*} - c)) (x^{*} - c) \\ = c - C f (c) + (I - C f^{'} (c + θ (x^{*} - c))) (x^{*} - c) \\ \in c - C f (c) + (I - C F^{'} ([x])) ([x] - c) \subseteq K ([x], c) . \end{matrix}$

2) 假设 $x^{*} \in [x]$ 为区间参数非线性方程组(2)的一个解，由(1)可知 $x^{*} \in K ([x], c)$ 这与条件相矛盾。所以 $[x]$ 不包含区间参数非线性方程组(2)的解。

3) 对于任意的 $f (x) \in f (x)$ ，定义 $p_{1} (x) = x - C f (x)$ ，则

$\begin{matrix} p_{1} (x) = c - C f (c) + x - c - C (f (x) - f (c)) = c - C f (c) + x - c - C f^{'} (c + θ (x - c)) (x - c) \\ = c - C f (c) + (I - C f' (c + θ (x - c))) (x - c) . \end{matrix}$

因为 $x, c \in [x]$ ，故 $c + θ (x - c) \in [x]$ ，所以

$p_{1} (x) \in c - C f (c) + (I - C F^{'} ([x])) (x - c) \subseteq K ([x], c)$ .

因为 $p (x)$ 在区间向量 $[x]$ 内连续且 $[x]$ 为非空有界闭凸集，如果 $K ([x], c) \subseteq [x]$ ，则 ${p_{1} (x) : x \in [x]} \subseteq [x]$ ，由Brouwer不动点定理可知至少存在 $p_{1} (x)$ 的一个不动点 $x^{*} \in [x]$ 使得 $C f (x^{*}) = 0$ 。又因为C为非奇异矩阵，所以 $f (x^{*}) = 0$ ，即 $[x]$ 一定包含非线性方程组 $f (x) = 0$ 的一个解，最后可得 $[x]$ 至少包含区间参数非线性方程组(2)的一个解。

命题1：设p为区间参数非线性方程组(1)中的区间参数，如果 $ω (P) = 0$ ，则改进的区间Krawczyk算子等价于区间Krawczyk算子。

很显然，改进的Krawczyk算子 $K ([x], c)$ 是映射 $p (x)$ 的区间扩展。基于Baumann的中点c的取值方法和引理1，定义

$K ([x], \underline{c}, \bar{c}) = [x] - C F ([x], \underline{c}, \bar{c}) = [x] - C (F_{N} ([x])) \cap F_{o} ([x], \bar{c}, \underline{c}) = [x] - C (F_{N} [x]) \cap F_{M} ([x], \underline{c}) \cap F_{M} ([x], \bar{c})$

其中 $\underline{c}$ 与 $\bar{c}$ 的定义见(3)和(4)。同时 $K ([x], \underline{c}, \bar{c})$ 与改进的Krawczyk算子具有相同的性质。

定理2：假设区间参数非线性函数 $f : D \subset R^{n} \to R^{n}$ 连续可微， $x^{*}$ 为区间参数非线性方程组(2)的任一实数解。则

1) $K ([x], c) \supseteq K ([x], \underline{c}, \bar{c})$ ；

2) 如果 $x^{*} \in [x]$ ，则 $K ([x], \underline{c}, \bar{c})$ ；

3) 如果 $K ([x], \underline{c}, \bar{c}) \cap [x] = \emptyset$ ，则区间 $[x]$ 内不含有区间参数非线性方程组(2)的任何解；

4) 如果 $K ([x], \underline{c}, \bar{c}) \subseteq [x]$ ，则 $[x]$ 一定包含区间参数非线性方程组(2)的一个解。

证明：

1) 因为

$K ([x], c) = c - C f (c) + (I - C F^{'} ([x])) ([x] - c) = [x] - C (f (c) + F^{'} ([x]) ([x] - c)) = [x] - C F_{M} ([x], c),$

由式(5)可知

$F_{M} ([x], c) \supseteq F_{o} ([x], \underline{c}, \bar{c}) \cap F_{N} ([x]),$

所以

$K ([x], c) \supseteq K ([x], \underline{c}, \bar{c}) .$

2)、3)、4)的证明与定理1的证明类似，不再赘述。

4. 求解区间参数非线性方程组的数值算法

对于区间参数非线性方程组，如果我们知道某区域一定存在解，可以用降阶的方法进行求解，每一步均可获得解的误差。其主要思想是将区间参数非线性方程组转化为区间参数非线性方程来进行求解。对于区间参数非线性方程组(2)，设 ${[x]}^{(k)} = {({[x]}_{1}^{(k)}, {[x]}_{2}^{(k)}, \dots, {[x]}_{n}^{(k)})}^{T}$ 为包含解的k次近似区间。在第i个分量方程 $f_{i} (x_{1}, x_{2}, \dots, x_{n}) = 0$ 中， $x = {(x_{1}, \dots, x_{n})}^{T}$ 的前 $i - 1$ 个分量 $x_{1}, \dots, x_{i - 1}$ 用新求出的 ${[x]}_{1}^{(k + 1)}, \dots, {[x]}_{i - 1}^{(k + 1)}$ 代替，而未计算出来的后 $n - i$ 个分量 $x_{i + 1}, \dots, x_{n}$ 仍用 ${[x]}_{i + 1}^{(k)}, \dots, {[x]}_{n}^{(k)}$ 来代替。可得关于 $x_{i}$ 的非线性方程 $f_{i} ({[x]}_{1}^{(k + 1)}, \dots, {[x]}_{i - 1}^{(k + 1)}, x_{i}, {[x]}_{i + 1}^{(k)}, \dots, {[x]}_{n}^{(k)}) = 0$ ，我们可以用求解非线性方程的迭代法进行求解，如牛顿法等。综上可得区间牛顿降阶法如下：

1) 当 $i = 1$ 时，利用区间牛顿法求解关于 $x_{1}$ 的方程 $f_{i} (x_{1}, {[x]}_{2}^{(k)}, \dots, {[x]}_{n}^{(k)}) = 0$ ，得 ${[x]}_{1}^{(k + 1)}$ ；

2) 当 $i = 2$ 时，利用区间牛顿法求解关于 $x_{2}$ 的方程 $f_{i} ({[x]}_{1}^{(k + 1)}, x_{2}, {[x]}_{3}^{(k)}, \dots, {[x]}_{n}^{(k)}) = 0$ ，得 ${[x]}_{2}^{(k + 1)}$ ；

3) ……；

4) 当 $i = n$ 时，利用区间牛顿法求解关于 $x_{n}$ 的方程 $f_{i} ({[x]}_{1}^{(k + 1)}, \dots, {[x]}_{n - 1}^{(k + 1)}, x_{n}) = 0$ ，得 ${[x]}_{n}^{(k + 1)}$ 。

定理3：如果区间向量 ${[x]}^{(k)}$ 包含区间参数非线性方程组(2)的解，则由区间牛顿降阶法所得的区间向量 ${[x]}^{(k)}$ 一定包含区间参数非线性方程组(2)的解。

证明：由区间牛顿法的性质 [13] 可得：定理成立。

当 ${[x]}^{(k + 1)} = {[x]}^{(k)}$ 且求解出来的区间向量 ${[x]}^{(k)}$ 达不到实际应用的需要时，我们可以采取区间二分法进一步细分区间向量，关于区间二分法的具体情况可参阅 [16] 。在求解过程中如果 $N ([x]) \cap [x] = \emptyset$ ，则 $[x]$ 中不包含区间参数非线性方程组的解，可将该区间删除。

对于区间参数非线性方程组，我们先利用改进的Krawczyk算子的分量形式寻求解的存在区域，然后利用区间降阶法求解实际问题需要的解区域(详见算法1)。

5. 数值算例

为了验证本文提出的算法1的可行性，这里选取了四个数值算例，使用区间工具箱INTLAB-V5.5在计算机(Intel i5, 2.6 GHz/4GB, MATLAB 2012b)进行计算，精度 $ε = 10^{- 13}$ ( $| x^{(k + 1)} - x^{(k)} | < ε$ 时迭代停止)。

例2：对于区间参数非线性方程组：

${\begin{cases} [0.9, 1.1] x_{1}^{2} + x_{2}^{2} - 1 = 0, \\ x_{1}^{2} - [0.9, 1.1] x_{2} = 0. \end{cases}$

初始区间为 $D = {([0, 1], [0, 1])}^{T}$ 。应用算法1，可得区间向量

${[x]}^{*} = {([0.73622, 0.83607], [0.54710, 0.68896])}^{T},$

区间向量的包含情况如图1。

例3：对于区间参数非线性方程组：

${\begin{cases} - x_{1}^{3} - 5 x_{1}^{2} - x_{1} + [1.9, 2.1] x_{2} - 3 = 0, \\ - [0.9, 1.1] x_{1} + x_{2}^{3} + x_{2}^{2} - 14 x_{2} - 19 = 0. \end{cases}$

初始区间为 $D = {([4.5, 5.7], [3, 4.7])}^{T}$ 。应用算法1，可得区间向量

${[x]}^{*} = {([4.98328, 5.016821], [3.98764, 4.01245])}^{T},$

区间向量的包含情况如图2。

例4：对于区间参数非线性方程组：

${\begin{cases} 2 x_{1} - [0.9, 1.1] x_{2} - 2 = 0, \\ - [0.9, 1.1] x_{1}^{2} - 4 x_{1} + 3.5 x_{2} + 5 = 0. \end{cases}$

初始区间为 $D = {([- 1, 1], [- 1, 1])}^{T}$ 。应用算法1，可得区间向量

${[x]}^{*} = {([0.85578, 1.0000], [- 0.26220, 0.02857])}^{T},$

Figure 1. Example 2: The solution set is in gray, outer rectangle is the result of Algorithm 1

图1. 例2：解集为灰色部分，外侧矩形部分为算法1的计算结果

区间向量的包含情况如图3。

例5：对于区间参数非线性方程组：

${\begin{cases} \sin (x_{1}) + \cos (x_{2}) - [- 0.52, - 0.5] = 0, \\ - 2 \cos (x_{1}) - 2 \cos (x_{2}) + [2.99, 3.01] = 0. \end{cases}$

初始区间为 $D = {([- 0.5, 1], [0.5, 1.5])}^{T}$ 。应用算法1，可得区间向量

${[x]}^{*} = {([- 0 .00533,0 .02503], [1 .04104,1 .05299])}^{T},$

区间向量的包含情况如图4。

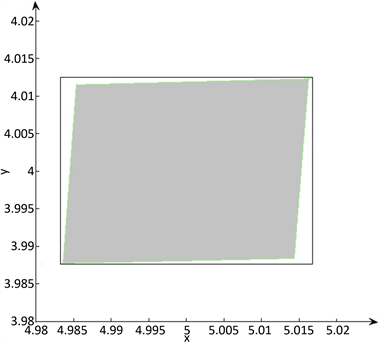
Figure 2. Example 3: The solution set is in gray, outer rectangle is the result of Algorithm 1

图2. 例3：解集为灰色部分，外侧矩形部分为算法1的计算结果

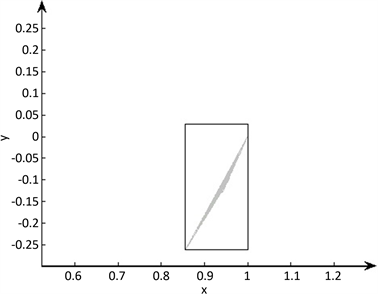
Figure 3. Example 4: The solution set is in gray, outer rectangle is the result of Algorithm 1

图3. 例4：解集为灰色部分，外侧矩形部分为算法1的计算结果

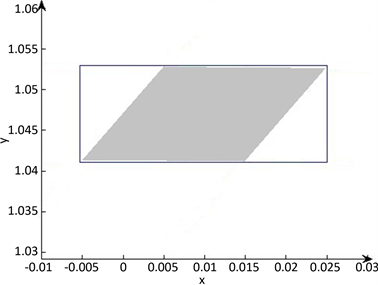
Figure 4. Example 5: The solution set is in gray, outer rectangle is the result of Algorithm 1

图4. 例5：解集为灰色部分，外侧矩形部分为算法1的计算结果

根据以上算例的数值计算结果可以看出，在计算精度内由算法1计算得到的区间参数非线性方程组的解集可充分包含其实际解集，进而说明了算法1的可靠性与有效性。

6. 总结

本文研究了区间参数非线性方程组的解集，在区间Krawczyk算子基础之上进行改进获得改进的区间Krawczyk算子并结合区间降阶法提出了求解区间参数非线性方程组的区间算法，最后通过数值算例表明算法1的可行性。

基金项目

本文工作由江苏省自然科学基金(NO.BK20151139)支持。

文章引用

王琪,肖旺,王海军. 求解区间参数非线性方程组的数值方法
Numerical Method for Solving Nonlinear Equations with Interval Parameter[J]. 应用数学进展, 2017, 06(07): 871-880. http://dx.doi.org/10.12677/AAM.2017.67105

参考文献 (References)

1. Tsai, L.W. and Morgan, A.E. (1985) Solving the Kinematics of the Most General Six and Five Degree of Freedom Manipulators by Continuation Methods. Journal of Mechanical Design, 107, 189-200. https://doi.org/10.1115/1.3258708

2. Gau, C.Y. and Stadtherr, M.A. (2002) New Interval Methodologies for Reliable Chemical Process Modeling. Computers & Chemical Engineering, 26, 827-840.

3. Meintjes, K. and Morgan, A.P. (1987) A Methodology for Solving Chemical Equilibrium Systems. Applied Mathematics and Computation, 22, 333-361. https://doi.org/10.1016/0096-3003(87)90076-2

4. Moore, R. (1966) Interval Analysis. Prentice-Hall, Inc., Englewood Cliffs, NJ.

5. Krawczyk, R. (1969) Newton-algorithmen zur bestimmung von nullstellen mit fehlerschranken. [Newton-Algorithms for Evaluation of Roots with Error Bounds.] Computing, 4, 187-201. https://doi.org/10.1007/BF02234767

6. Hansen, E. (1992) Global Optimization Using Interval Analysis. Monographs and Textbooks in Pure and Applied Mathematics, Vol. 165, Marcel Dekker, NY.

7. Nikas, I., Sotiropoulos, D. and Grapsa, T. (2006) Extending interval Newton Method for Nonlinear Parameterized Equations. In: Simos, T., Psihoyios, G. and Tsitouras, C., Eds., ICNAAM-International Conference on Numerical Analysis and Applied Mathematics, Wiley-VCH, Hersonisos, Crete, 512-515.

8. Nikas, I. and Grapsa, T. (2009) Bounding the Zeros of an Interval Eq-uation. Applied Mathematics and Computation, 213, 466-478. https://doi.org/10.1016/j.amc.2009.03.041

9. 邱亮, 王海军, 王琪. 求解区间非线性方程的一类改进算法[J]. 应用数学进展, 2017, 6(5): 716-725.

10. Moore, R.E. (1977) A Test for Existence of Solutions to Nonlinear Systems. SIAM Journal on Numerical Analysis, 14, 611-615. https://doi.org/10.1137/0714040

11. Alefeld, G. and Herzberger, J. (2012) Introduction to Interval Computation. Academic Press, Burlington.

12. Zhang, D.Q., Li, W.G. and Shen, Z.H. (1999) Solving Underdetermined Systems with Interval Methods. Reliable Computing, 5, 23-33. https://doi.org/10.1023/A:1026489507711

13. 王德人, 张连生, 邓乃扬. 非线性方程组的区间算法[M]. 上海: 上海科学技术出版社, 1987: 30-31.

14. Baumann, E. (1988) Optimal Centered Forms. BTL Numerical Mathematics, 28, 80-87. https://doi.org/10.1007/BF01934696

15. Wang, H.J. and Cao, D.X. (2009) Interval Expansion Method for Nonlinear Equation in Several Variables. Applied Mathematics and Computation, 212, 153-161. https://doi.org/10.1016/j.amc.2009.02.008

16. Moore, R.E. and Jones, S.T. (1977) Safe Starting Regions for Iterative Methods. SIAM Journal on Numerical Analysis, 14, 1051-1065. https://doi.org/10.1137/0714072

期刊菜单