Advances in Applied Mathematics
Vol.
13
No.
01
(
2024
), Article ID:
79106
,
6
pages
10.12677/AAM.2024.131009
N股Montesinos纽结的着色Jones多项式
马郡梓,冷旭东*,班子涵
辽宁师范大学数学学院,辽宁 大连
收稿日期:2023年12月10日;录用日期:2024年1月5日;发布日期:2024年1月12日

摘要
本文运用纽结三价图计算了当 时,n股Montesinos纽结的着色Jones多项式。算法的关键是构造从 图到n股Montesinos纽结的三价图变换过程,该算法与 的情况有着本质不同。
关键词
着色Jones多项式,纽结三价图,Montesinos纽结

The Colored Jones Polynomial of N-String Montesinos Knots
Junzi Ma, Xudong Leng*, Zihan Ban
School of Mathematics, Liaoning Normal University, Dalian Liaoning
Received: Dec. 10th, 2023; accepted: Jan. 5th, 2024; published: Jan. 12th, 2024

ABSTRACT
In this paper we calculate the colored Jones polynomial of n-string Montesinos knots for using knotted trivalent graphs. The key point of the algorithm is to construct the operations from a graph to a Montesinos knot, and the algorithm has essential difference with the case .
Keywords:Colored Jones Polynomial, Knotted Trivalent Graph, Montesinos Knot

Copyright © 2024 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
纽结可看作 在 中的嵌入,它的分类问题是三维流形中的重要课题,而多项式不变量在这其中发挥了重要作用。1984年,V. Jones [1] 在算子代数的研究中意外发现了著名的Jones多项式,作为它的推广,着色Jones多项式(colored Jones polynomial)在1986年E. Witten [2] 运用拓扑量子场论率先发现,后由N. Reshetikhin等人 [3] 给出其数学上严格的定义:一般地,对任一半单复李代数g,对其泛包络代数进行形变从而得到对应的量子群,它上面存在一种特殊的Hopf代数结构使得人们能够通过表示论构造相应的纽结不变量。当 ,取N维表示时,对应着色Jones多项式。这种由量子群构造不变量的方法具有重要理论意义,但其具体计算往往复杂。对于着色Jones多项式,R. van der Veen等人 [4] 率先采用纽结三价图(knotted trivalent graph,下文简称KTG)针对三股排叉结的情形进行了计算,其算法大意如下:着色Jones多项式可以推广到KTG上,而纽结可看作是一种特殊的KTG,且任一KTG可由 图经过三种基本变换得到,所以只要利用着色Jones多项式在这三种KTG变换下的变换公式,就能得到相应纽结的着色Jones多项式。本文的目的就是运用这种方法得到n股Montesinos纽结( )的着色Jones多项式,而该算法的核心部分与 的情况 [5] 有着本质不同,并不能看作后者的简单推广。
2. 预备知识
定义2.1
1) 一个标价图是一个一维单纯复形 连同其嵌入 ,其中 是一个带边曲面,且此嵌入的像是 的脊(spine)。
2) 一个纽结三价图(KTG)是一个嵌入在 里的三价标架图(作为曲面)。
3) 设 是一个纽结三价图, 是它的所有边组成的集合,V是它所有顶点组成的集合。一个 的允许着色是一个映射 ,其中 ,其中 是顶点v相邻的三个着色满足如下两个条件:
① 是偶数。
② (三角不等式)。
纽结三价图的特点在于其上存在一些有用的变换。这里我们主要用到如下三种变换:扭转 ,分裂 和三角变换 ,如图1,在边e上进行扭转F和分裂U,在顶点 上进行三角形变换 。
引理2.1 [6] 任意一个纽结三价图都可以由 图通过反复运用扭转,分裂和三角变换而得到。
由此,我们一旦定义了 图的着色Jones多项式,并且能描述它如何随着以上三个变换而变换,那我们就能定义任意一个纽结三价图的着色Jones多项式。
定义2.2 [4] 一个带有允许着色 的纽结三价图 的着色Jones多项式 是由如下关于 图和KTG变换的公式定义的。
,
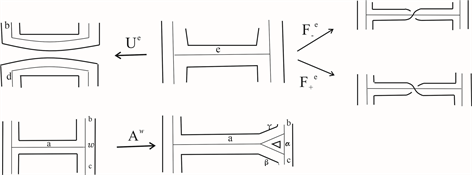
Figure 1. Operations on KTGs
图1. 纽结三价图上的三种变换
,
,
.
其中对称多项式系数定义如下:
,
量子整数定义为
.
k-着色的平凡结的Jones多项式定义如下:
.
扭转变换f定义如下:
.
在分裂变换的公式中,求和的范围是取尽被分裂的边e的所有可能的允许着色(由 之间的三角不等式推出)。
,
其中,求和指标z的取值范围由二项式系数给出,且有
.
特别地,一个纽结是一个没有顶点的0-标架(0-framed)纽结三价图。这里我们将纽结K的着色Jones多项式重新定义为 ,其中n是纽结K的单独边上的着色,且 是用来将平凡结的值规范成 。
3. Montesinos纽结的着色Jones多项式
Montesinos纽结是一类具有代表性的纽结,它由若干个有理缠结(rational tangle)排成一圈相连生成,本文我们研究n股Montesinos纽结 ,如图2。
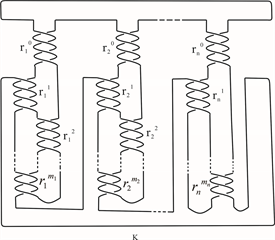
Figure 2. Montesinos knot
图2. Montesinos纽结
定理3.1 设K是Montesinos纽结 ,其中 , ,则K的着色Jones多项式为
其中 , 都是偶数且满足:
,
, .
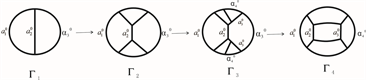
证明:如图3,注意,图中没有被标记着色的边默认用n着色。从 图开始,我们先在两个顶点处各做一个三角变换得到图 ,且有
.
在 的两个三角形的右侧顶点分别做一次三角变换得到图 ,再对 进行分裂得到图 ,且有 。
然后对最右侧的两个顶点做三角变换,再对 进行分裂,依次做下去得到图 ,则有
 (a)
(a)
 (b)
(b)
 (c)
(c)
 (d)
(d)
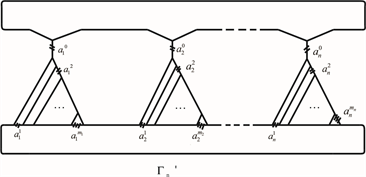
Figure 3. Operations from a graph to a Montesinos knot
图3. 从 图到Montesinos纽结的变换
在 中每个 所在边的下顶点进行 次三角变换得到图 ,同时有
.
然后在 中对对每个被标记的边做相应的扭转,最后对这些扭转的边做分裂变换就得到了纽结K。注意对一个扭转的边做一个分裂变换会生成两个扭转的边,且两个边保持相同的扭转数。需要注意的是,为了得到Montesinos纽结的着色Jones多项式,我们需要消去由变换产生的标架 和由拧数产生的标架 。
,
.
所以最终的结果应该乘上因子 。□
我们看到,在 的情形中,运用纽结三价图计算着色Jones多项式需要通过更多的三角和分裂变换引入一类新的指标 ,这与 的情形有着本质不同,故这一算法的计算效率有待进一步研究。此外,我们注意到S. Garoufalidis等人 [7] 为了处理此类 的情形采用了聚变(fusion)和拆接(skein)理论的方法。
基金项目
国家自然科学基金项目(12001255)。
文章引用
马郡梓,冷旭东,班子涵. N股Montesinos纽结的着色Jones多项式
The Colored Jones Polynomial of N-String Montesinos Knots[J]. 应用数学进展, 2024, 13(01): 70-75. https://doi.org/10.12677/AAM.2024.131009
参考文献
- 1. Jones, V.F. (1985) A Polynomial Invariant for Knots via Von Neumann Algebras. Bulletin of the American Mathemati-cal Society, 12, 103-111. https://doi.org/10.1090/S0273-0979-1985-15304-2
- 2. Witten, E. (1989) Quantumfield Theory and the Jones Polynomial. Communications in Mathematical Physics, 121, 351-399. https://doi.org/10.1007/BF01217730
- 3. Reshetikhin, N. and Turaev, V.G. (1991) Invariants of 3-Manifolds via Link Polynomials and Quantum Groups. Inventiones Mathematicae, 103, 547-597. https://doi.org/10.1007/BF01239527
- 4. Lee, C.R.S. and van der Veen, R. (2016) Slopes for Pretzel Knots. The New York Journal of Mathematics, 22, 1339-1364.
- 5. Leng, X., Yang, Z. and Liu, X. (2019) The Slope Conjectures for 3-String Montesinos Knots. The New York Journal of Mathematics, 25, 45-70.
- 6. Thurston, D.P. (2002) The Al-gebra of Knotted Trivalent Graphs and Turaev’s Shadow World. Geometry & Topology Monographs, 4, 337-362.
- 7. Garoufalidis, S., Lee, C.R.S. and Roland, V.D.V. (2018) The Slope Conjecture for Montesinos Knots. arXiv.1807.00957.
NOTES
*通讯作者。