Dynamical Systems and Control
Vol.
07
No.
04
(
2018
), Article ID:
27296
,
10
pages
10.12677/DSC.2018.74036
Review of Synchronous Control Methods in Complex Networks
Xing Jia, Haiyi Sun*
School of Science, Shenyang Jianzhu University, Liaoning Shenyang

Received: Oct. 3rd, 2018; accepted: Oct. 19th, 2018; published: Oct. 26th, 2018

ABSTRACT
In recent years, there are more and more researches on complex networks in China. With the deepening of research, people have a higher degree of understanding of complex networks, and many research results have been applied to the actual production and life. Among them, the research on synchronization characteristics of complex networks is more concerned by people, so the introduction is largely about the related research and results of complex network synchronization control methods at home and abroad. Through collecting and sorting out a large number of domestic and foreign historical documents and materials, this paper makes an overall grasp of the recent research on the synchronization control of complex networks by using the methods of literature review and theoretical research. The content of this paper includes the research of complex network synchronization control by domestic and foreign researchers and the discussion of the development process of complex network synchronization control research using contrast method. The single analysis mainly involves the comparison between control methods and the comparison before and after the development of the same method. In this paper, the background, development and significance of the research on complex networks are introduced firstly. The main control methods are: Pinning control, impulse control, adaptive control and intermittent control. The main control methods are as follows: Containment control, impulse control, adaptive control and intermittent control. The main research method mentioned in this paper is simulation, and the research object is the mathematical model of complex network. Therefore, the common network model and related parameters are introduced. At the same time, at the end of the article we summarize the previous research results and put forward some of the issues discussed in the current research.
Keywords:Complex Dynamic Network Model, Synchronization Characteristics, Synchronization Control Method, Pinning Control, Intermittent Control, Adaptive Control
复杂网络同步控制方法研究综述
贾兴,孙海义*
沈阳建筑大学理学院,辽宁 沈阳

收稿日期:2018年10月3日;录用日期:2018年10月19日;发布日期:2018年10月26日

摘 要
近年来国内关于复杂网络的研究越来越多,随着研究的深入人们对复杂网络的认识程度也越来越高,许多研究成果被应用到实际的生产生活当中。其中对于复杂网络的同步特性的研究是比较受人们关注的,因此本文主要介绍的是国内外有关复杂网络同步控制方法的相关研究及成果。通过搜集、整理大量的国内外历史文献资料利用文献综述法和理论研究法对近年来有关复杂网络同步控制的研究进行整体把握,本文所涉及的内容包括国内及国外研究人员对复杂网络同步控制的研究并且各部分以时间为顺序进行论述运用对比法对复杂网络同步控制研究的发展过程进行简单的分析主要涉及控制方法之间的比较以及同一方法发展前后的对比。本文首先介绍了复杂网络这一科学领域产生的背景、发展和相关研究的重要意义,介绍的控制方法主要有:牵制控制、脉冲控制、自适应控制和间歇控制。文中所提到的研究方法以仿真模拟为主,研究对象则是复杂网络的数学模型因此对常见的网络模型及先关参数进行了介绍。同时在文章最后总结了之前的相关研究结果并提出了一些在目前研究当中论述较少的问题。
关键词 :复杂动态网络模型,同步特性,同步控制方法,牵制控制,间歇控制,自适应控制

Copyright © 2018 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
从互联网到万维网、从电力网到交通网、从生态网到人类社会关系网、小到生物神经网、大到科研合作网以及各种政治、经济关系网,复杂网络的概念已经不仅限于渗透到了各个学科领域当中 [1] ,不仅是科学研究方面随着信息时代的到来人们更清楚的认识到我们每一个人都生活在由人类与地球上各种事物构成的多种多样的复杂网络当中。世界因此向着全球化的方向发展,人们也享受到科技发展带来的便利,如无线手机通话、互联网等技术使得世界上的事物联系越来越紧密。但是这一变化也带了很多新的问题,和针对生物的疾病传播一样针对不同的网络也存在着具有破坏性的恶意攻击,如计算机病毒的大面积传播、部分电力系统故障导致大面积停电等。因此随着人类生活环境的网络化程度越来越高要求人们要对各种人工和自然网络系统定性的特征与定量的规律进行深入的研究,由此更好的认识这些复杂网络并使其可以有效地被人类利用。长期以来,各个学科领域都针对各自的研究对象进行了大量的观察和研究,如通信科学中的通信网络、电力科学中的电力网络、生命科学中的生物网络和社会科学中的社会网络等 [2] ,但是这些看似联系并不紧密的研究对象本质上都是复杂网络。今天随着网络科学和计算机科学技术的快速发展复杂网络的相关研究逐渐成为一个新的独立的研究方向,各学科领域针对网络的研究被这一全新的科学研究分支所包揽,各学科理论及应用呈现交叉、渗透和融合的发展趋势 [3] [4] 。对复杂网络的研究主要是从抽象的数学模型出发研究各种复杂网络所具有的共性以及对其加以控制利用的普遍方法。本文将在接下来的内容当中将对复杂网络模型的建立过程及现有的控制理论成果进行简单的介绍。
2. 现代网络科学的发展
1736年Euler解释了著名的哥尼斯堡七桥问题,由此开创了图论与几何拓扑并成为了数学一个全新的研究领域,同时也可以认为是网络科学的开端。此时的网络科学属于图论的研究范围,早期的网络研究主要是数学家和物理学家针对一些可用简单规则网络进行观察研究。到1960年前后Erdös建立起了严格的数学随机图论Erdös与Rényi在传统图论的基础上做出了重大突破提出了一种完全随机的网络模型是网络科学发展的又一个里程碑。随着研究的深入与信息化科技的发展人们发现这种模型存在着很大的局限性。许多科技工作者为了更深入有效的研究复杂网络在模型的建立做出了贡献,其中在1998年Watts和Strogatz提出的小世界网络模型,以及1999年Newman和Watts对小世界网络模型进一步改良建立了“单标度”网络模型。以及后来为了合理解释现实网络中连接分布呈现幂律分布的规律Barabási和Albert提出了著名的无标度网络模型成为了网络科学研究一个标志性的新进展。以上提到的随机网络模型、小世界网络模型、无标度网络模型是三个具有代表性的复杂网络模型。时至今日复杂网络的研究正在繁荣发展,既有对原有理论、方法的扩展和填充,也有各种新观点、新思想、新方法的大量出现。但是对于复杂网络的研究仍然还有很长的路要走,在很多方面还需要深入研究对之前的研究成果进行完善,需要之后的研究者通过不断地研究填补空白点。
3. 复杂网络的基本模型及参数
从复杂网络研究的起源可以看出最早的相关研究属于数学领域的研究分支,因此可以用数学的方法去定义网络。从数学的角度来说网络可以定义为一幅图,节点和边是构成图的基本元素相应的在网络中也有节点和边的存在,如互联网中的一台电脑或主机、万维网中的一个网站、社会网中的一个人或一个集团、通信网中的一个移动终端、生物网中的一个生物个体或物种、神经网中的一个神经元细胞等,都可以看成是网络中的一个节点。而边则是表示节点与节点间的某种特殊关系,如互联网物理层中的一条光纤、万维网中的一个链接通路、社会网中的一层关系、通信网中的一次会话、生物网中的食物链、神经网中的一个经络等。对于不同网络的节点间相互联系起来的联结方式是不同的所以不同的网络就有其自己特有的拓扑方式,从宏观上表现为网络的性质各不相同每一个网络都存在其特性,因此针对每一种网络的定性定量研究就成为利用网络的关键,作为研究网络的主要手段建立可靠的网络模型也要针对所研究的网络进行相应的调整。接下来将对网络模型中的一些重要参数和上面提到的三种网络模型及其性质进行介绍。
3.1. 主要参数
这个部分只列举参数并解释基本含义,在下文中重要网络模型的性质部分中会对不同网络模型的重要参数进行介绍。
度(degree)和度分布(degree distribution):度是一个反映节点在网络中与其他节点连边情况的量。通常我们定义一个节点具有的与其他节点连边的数目总和为该节点的度,如果1个节点与除其本身以外的n个节点有连边那么这个节点的度为n。度分布是对于网络中节点的度的总体的描述,将具有相同度数的节点统计在一起并以度数为横坐标节点个数为纵坐标建立可以建立起一个分布图,这就类似于常见的学生成绩分布图可以直观地反映出不同网络模型度数的分布特性。如随机网络模型与小世界网络模型的度服从泊松分布,无标度网络模型的度则服从幂律分布,由此可以看出具有相同性质的不同网络可以具有相同的度分布,但值得注意的是即便是有相同的度分布其分布中的各参数值有可能是不相同的。
距离(distance)和平均最短路径长度(average shortest path-length):在网络模型中距离表示一个节点到另一个节点的最短连边的条数,这是距离最常用也是最简单的一种定义方式。如在一个网络模型中节点A与它的邻居节点B,即A与B之间有边直接相连那么它们的距离是1,如果节点B也存在一个邻居节点C且A与C之间不存在边相连,那么A和C的距离就是2。一个网络上所有的节点距离的平均值就是这个网络的平均最短路径长度。
群集系数(clustering coefficient):为了研究网络中的某一个节点它的直接邻居节点之间相互连接的稠密程度,人们提出了群集系数这个概念。群集系数的取值范围为0到1之间,假设网络中节点A的度为N,即A与其他n个节点相连(A有n个邻居节点)如果这n个邻居节点又全都相互连接则A的群集系数为1,反之如果A的所有邻居节点均互不相连则A的群集系数为0。将网络中所有节点的群集系数取值求平均值得到一个取值范围在0到1之间的实数,这个数就是整个网络的群集系数。星形规则网络和全连接的规则网络在说明这个问题上具有很好的代表性,星型规则网络中节点的邻居节点之间都不相互连接,星型规则网络的群集系数是0;全连接的规则网络从其名称就可以知道网络中所有节点都相互连接,因此任意节点的群集系数都为1整个网络的群集系数也是1。
介数(betweenness):网络中两两相连的节点对之间通过该节点的所有连边的总数量称为节点介数;网络中两两相连节点对之间通过该边的所有连边的总数量称为连边介数,从概念上来说介数可以理解为在网络上通过人们关注的节点或者连边的数据流通量 [2] 。显然,在讨论网络数据流通管理控制时,节点介数比节点度常常更为重要;但是节点度相对容易计算获得,而节点介数很难进行计算因此有关节点介数的讨论相对较少。一个网络的节点(连边)平均介数就是网络上所有节点(连边)介数的平均值,一般来说,网络介数随着网络稠密程度的提高增加,相对稠密的网络比相对稀疏的网络介数要高。
3.2. 网络模型
在对不同的复杂网络进行研究时由于不同网络即存在着不同的特性和参数,如不同的网络节点度数存在差异,在某些方面又具有相似的特性,如现实生活中的许多复杂网络度分布都具有“幂律截尾”。因此首先要建立相应的数学模型来描述复杂网络,目前对网络模型的分类没有一个明确的标准,通常人们根据网络的生成方式大致上将复杂网络划分为三大类:规则网络、随机网络以及介于这两种极端情况之间的网络模型(图1)。
规则网络是研究历史最长的一类网络模型,包括全连接网络、星形、环形、链形网络等规则且具有确定性的网络。规则网络具备节点群集系数高、平均最短路径长的特点。由于其结构简单研究起来也比较容易所以不做过多介绍。现实世界中存在的网络的模型大多属于第三种既具有一定的规则但也有一定的随机性,如之前提到的比较重要的小世界网络模型和无标度网络模型。

Figure 1. Network structure diagram [5]
图1. 网络结构示意图 [5]
3.2.1. 随机网络模型
将随机图 [6] (也称ER随机图论)的数学理论应用于网络研究则称为随机网络模型,这种模型描述为:由n个节点构成,每个节点两两之间都是相互连接的则边的总数为 条,从这些边中随机选取m条边由这些边和节点可以构成一个网络,有这种随机选取的方法构成的网络总共有 种可能的情况,且每种网络是等可能出现的(出现概率相同)。如图2所示为随机网络模型 [5] 。
随机网络的大部分节点的节点度相近,在很多文献中也都提到随机网络的这种度分布服从泊松分布的性质,随机网络还具有较小的平均路径长度和较小的群集系数的性质 [7] 。到20世纪90年代末这种网络模型作为描述复杂网络的重要工具。
3.2.2. 小世界网络
随着现代科技的发展计算机在数据处理等方面的能力得到了很大的提高使人们可以对很多现实生活中的复杂网络进行仿真试验,在对大量的结果进行分析时人们发现现实世界中绝大多数的网络即不能用规则网络模型描述也不能用随机网络模型进行描述,于是提出了一些更符合实际的网络模型,即介于规则网络和随机网络之间的一类网络模型 [8] ,其中就包扩小世界网络和无标度网络模型 [9] [10] 。已知一个具有n个节点的规则环形网络,且其环上每一个节点都与其他m各节点相连,即每个节点都有m条边相连,对每一条边都以概率p进行断开然后在与除自身以外的其他节点进行重新连接(不能进行重复连接),由此规则生成的网络模型被称为小世界网络模型。如图3所示为小世界网络模型 [5] 。
根据小世界网络的生成规则可以看出重新连接的节点也是随机的新生成的边所连接的两个节点距离可能很远也可能很近,将连接距离较远的边称为“长程边”。不难看出因长程边的存在小世界网络模型具有较小的平均最短路径长度,而且重新连接操作对节点的群集系数影响不大,所以小世界网络区别于规则网络和随机网络的特点就是同时具有较小的平均最短路径长度和较大的群集系数。同时小世界网络模型节点的度分布近似服从泊松分布。
3.2.3. 无标度网络模型
在人们对现实生活中的网络进行研究观察的时候发现许多网络具有大规模的高度自组织特性,其中网络节点度分布近似服从幂律分布即大多数节点具有相近的度数,极少数节点具有较大的度数。通过对网络这一特点的研究发现,假设一个网络随机的加入一个节点,而新加入节点在与网络中已有节点进行连接时会较大概率的连接度比较大的节点,我们理解为优先连接度比较大节点这就是择优连接特点,是无标度网络的一个重要特点也是生成无标度网络的重要规则。如图4所示为无标度网络模型 [5] 由这个特点我们可以分析出无标度网络具有较小的平均最短路径长度和较小的群集系数。
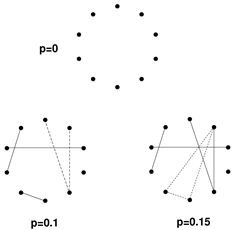
Figure 2. Stochastic network model
图2. 随机网络模型
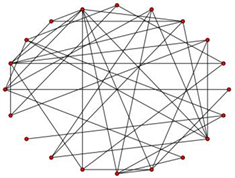
Figure 3. Small-world network model
图3. 小世界网络模型

Figure 4. Scale-free network model
图4. 无标度网络模型
以上三种网络模型是在复杂网络研究过程中出现的具有代表性的网络模型,如之前所提到的现实网络大多即不是规则的也不是完全随机的,虽然小世界和无标度网络至今都是研究现实网络的重要手段,但是并不是说小世界和无标度网络模型可以描述所有网络的特征,比如有些的网络同时具备小世界和无标度两种网络的一些基本性质,近10年来,复杂网络的研究开展得更加广泛,随着研究的深入也会提出更适合描述现实网络的模型,很多目前没有解决或不能解决的问题也会被逐一解决。
在复杂网络的研究中人们发现复杂网络的同步现象普遍存在于与人类关系密切的诸如通信网络、电力网络等复杂网络中。同步现象的发现最早可以追溯到1665年惠更斯观察到的固定在同一个杆上的两个钟摆在一段时间后钟摆的摆动会趋于同步,之后在1680年有人观察到萤火虫的闪烁从起初的无序逐渐趋于同一频率。现在通过人们的研究这种趋于“统一”的现象普遍存在于自然界和人类社会当中。复杂网络同步的研究对于复杂网络系统存在着重要的意义,同步可以使复杂网络系统的功能得到优化。对于复杂网络模型来说同步是指节点之差为0 [11] 。但是在研究中发现许多复杂网络想要达到同步状态或者两个至多个复杂网络达到同步状态需要人为的施加控制。因此人们开始研究复杂网络的同步控制方法通过施加合适的控制器使网络趋于同步状态来提高复杂网络的各方面性能。
4. 复杂网络同步控制的基本方法
在控制中控制方法是研究的主要问题,随着对复杂网络控制研究的深入产生了许多的控制方法。这些方法可以宏观的分为两大类:第一类是传统控制策略,主要包括PID控制、解耦控制;第二类是现代先进控制策略,这类控制策略相较传统的控制策略具有更好的适应性。因此随着网络的复杂程度以及人们对控制精度和性能要求的不断提高现代先进控制策略扮演着主要角色,传统的控制策略则包含在先进控制策略当中。针对不同网络结构和控制需要现代先进控制策略也多种多样主要有:线性控制、脉冲控制、间歇控制、采样控制、模型预测控制、模糊控制、牵制控制等。其中牵制控制是从网络结构的角度来看,其他几种控制策略是从设计方法和实现手段来划分,所以在实际应用当中牵制控制与其他几种控制策略相结合衍生出如脉冲牵制控制、间歇牵制控制等控制方法。
4.1. 牵制控制
牵制控制是一种控制方法,其主要目的是通过控制复杂网络系统中的少数节点来控制整个复杂网络,在说明这种控制方法的时候通常会引入线虫神经元和生物族群蜂拥现象等经典例子来进行解释。例如,线虫是生物界中一种具有相对简单神经系统的生物方便人类研究,因此在神经系统研究方面对线虫的认识研究也是比较清楚地,在对线虫神经系统进行研究时人们发现线虫共有约300个神经元和约2400条神经连接线,而通过刺激少数(平均49个)神经元就可达到控制全身神经的目的,这些神经元仅占线虫全身神经元的17%属于少数个体,但通过对这些少数个体的控制却可以达到控制整个系统的目的。生物学中的这一发现为控制复杂网络提供了一种新的思路。
随着复杂网络的结构复杂度提高网络的全局信息很难掌握对网络中每一个节点施加控制很难实现有的时候也不能满足经济的要求,这种可以通过局部控制来实现对复杂网络进行全局控制的控制方法成为了人们研究的热点。通过大量的研究证明选择适当的耦合强度和反馈增益是可以实现的。
Wang和Chen等人在2002年 [12] [13] 分析了无标度网络的幂律分布特性,并基于这一特性提出了局部施加反馈控制来对无标度复杂网络进行控制,不仅给出了局部控制的理论模型还给出了仿真试验的结果数据,从理论和数字上都严格的验证了局部控制的可行性,在国内首次提出了牵制控制。除此之外文章中还提到了控制器的放置方法,即在度数大的节点上放置控制器更有效。Chen和Fan等人在2005年 [14] 提出了牵制控制作用下的复杂动态网络的数学模型:
其中
是施加的控制,
表示受控节点个数。同时在这篇文章中提到了两种常见的控制策略,一种是特定牵制控制即按照节点度由高到低选取网络中的一些节点进行控制,另一种是随机牵制控制即随机选取一部分节点进行控制。在文献 [14] 中同时指出了特定牵制控制比随机牵制控制更有效。值得关注的是陈天平等人在2007年给出了只对一个节点进行控制就可以实现对整个网络进行控制的相关研究结果,但是具有一定的局限性这个结果是在内部耦合函数为单位矩阵条件下得到。同年占萌 [15] 等人给出了在不同内部耦合函数网络中控制一个节点使网络同步的参数条件。在文献 [4] 中Chen结合Lyapunov稳定性理论论述了网络系统的同步区域,并讨论了常见的几种同步区域(S)形式和耦合强度(c)与稳定区域的关系 [16] [17] [18] [19] [20] 。第一类是文献 [16] [17] 对应的同步域 ,具有这种类型的同步域的网络其Laplace矩阵的最小非零特征根越大说明网络同步能力越强所需要的耦合强度越小;第二类是文献 [18] 对应的同步区域
,具有这类同步区域的网络其同步能力往往通过非零特征根比率来描述,比值越大网络同步能力越强;第三类是文献 [16] [17] [18] 对应的同步区域为空集的一种情况,具有这种同步域的网络不能自我实现同步(需要人为对其进行控制);第四类是文献 [19] [20] 对应的同步域是多个
的并集构成的,这种情况相对比较复杂而且不常见。这个结论可以有效地反映出网络系统的同步能力与耦合强度之间的关系。在此基础之上Chen还在文章中论述了网络的结构在解决牵制控制器设计与放置等问题上的关键作用。
,具有这种类型的同步域的网络其Laplace矩阵的最小非零特征根越大说明网络同步能力越强所需要的耦合强度越小;第二类是文献 [18] 对应的同步区域
,具有这类同步区域的网络其同步能力往往通过非零特征根比率来描述,比值越大网络同步能力越强;第三类是文献 [16] [17] [18] 对应的同步区域为空集的一种情况,具有这种同步域的网络不能自我实现同步(需要人为对其进行控制);第四类是文献 [19] [20] 对应的同步域是多个
的并集构成的,这种情况相对比较复杂而且不常见。这个结论可以有效地反映出网络系统的同步能力与耦合强度之间的关系。在此基础之上Chen还在文章中论述了网络的结构在解决牵制控制器设计与放置等问题上的关键作用。
4.2. 脉冲控制
在很多时候复杂动态网络的节点受到瞬时扰动或其他原因引起的突发性噪声影响会使节点的状态发生变化,为了应对这类问题人们研究了脉冲控制。脉冲控制能使不稳定系统变得稳定;也可以使原本稳定的系统变得不稳定等。 [21] 如在经济方面我国的宏观调控中就存在着这种控制方法。 [22] 脉冲控制是指在离散的时间点对系统施加脉冲控制量使系统状态发生改变的一种非连续的控制手段。脉冲控制的研究从1960年Millman和Myshkis首次提出脉冲控制系统作为开端 [23] 。1989年V. Lakshmikantham等人 [24] 首次提出脉冲微分系统。Yan和Shen于1998年基于Soliman利用“Lyapunov直接法”得到的脉冲系统稳定规则进一步提出了稳定判定方法 [25] 。在此之后又越来越多的学者开始关注脉冲控制相关的理论也越来越完善,文献 [21] [22] [21] [24] 对此有详细的论述。2016年Liu等人 [26] 在其文章中介绍了一种将脉冲控制与牵制控制相结合的一种控制方法,文中同时介绍了一种建模框架这种框架是许多现有连续时间和离散时间CDN模型的统一和推广,针对这一模型在不同的离散脉冲点对不同的节点施加牵制控制,得到了连续和离散复杂动力系统同步的稳定条件,即利用脉冲牵制控制对网络进行控制的同步条件。
4.3. 自适应控制
自适应控制是指控制器可以通过调整自身的参数来适应受控网络本身或受控网络受到所处的环境扰动影响的一种控制手段,早期的自适应控制只是在对具体问题设计解决方案时的一种手段并未形成相关的理论体系。随着对复杂网络系统控制的发展以及许多学者对这一方法的控制结构、稳定性等方面进行深入研究并取得了突破使得自适应控制理论的研究进入到了系统化的阶段。自适应控制可以分为四种:变增益自适应控制、模型参考自适应系统(MRAS)、自校正调节器和直接优化指标函数的自适应控制。 [27] 变增益自适应控制的原理比较简单,调节器按照系统的状态(通过对获取的某些变量进行计算)对控制器施加的增益等参数进行调整具有反应迅速等优点,但由于控制器获取系统数据的局限性导致这种控制方式在某种程度上不能对参数进行最优的调整。模型参考知识性系统则是对变增益自适应控制的一个改进,在原有的自适应回路(内环)基础上加入另一个自适应回路(外环)来调节控制器的参数来减小输出的误差使内环的特性与受控模型基本一致。这种自适应控制手段比之前的具有更好的性能,但由于存在零极点对消的问题这种控制器的适用范围具有一定的局限性。自校正调节器是将在变增益自适应控制与在线受控系统参数估计相结合,由独立的参数估计部分对受控系统进行参数估计并将数据传输给调节器称为显式自校正调节器,由调节器参数表示受控系统参数进行估算则可以省去独立的参数估计部分使系统得到一定程度上的简化称为隐式自校正系统。这种自适应控制方式较多的应用于离散系统控制当中。直接优化指标函数的自适应控制与模型参考自适应系统和自校正调节系统有着相似的模型结构,选定某个特定的指标函数,是一种基于系统输出、参数变量、控制信号等数据进行计算得出优化自适应控制的算法。
4.4. 间歇控制
复杂网络同步控制的方法多种多样其中间歇控制是一种更容易实现并且能量消耗更小的一种同步控制方法,最初间歇控制被应用于经济学领域,随着其逐步的发展与成熟间歇控制在诸如管理系统、医疗系统中都有所应用。如下:
是一种间歇控制器的模型,从模型可以直观地看出间歇控制与之前介绍的牵制控制、自适应控制这两种控制方法不同,之前提到的这两种控制方法都是连续的。间歇控制与脉冲控制类似,是非连续的在固定周期内施加控制,在其他时间控制器对受控网络不施加控制,而脉冲控制与间歇控制的不同在于脉冲控制是在特定时间点施加控制,间歇控制是在特定时间段内施加控制 [28] ,间歇控制也由此被认为是一种介于脉冲控制和连续控制方法之间的过渡 [29] 。间歇控制在某些情况下比连续控制方法更加经济高效。但在降低成本和能耗的同时也带来了控制性能降低的问题使控制系统稳定所需要的时间消耗相对提高。
2000年,Zochowski在其文章中首次运用间歇控制方法对非线性动力系统进行控制。在《复杂动力网络的同步分析与控制》 [30] 书中也提到Zochowski在文中采用的控制器均为线性反馈控制,所的增益系数比实际需求要大。针对这一问题书中介绍了运用Lyapunov稳定系定理,结合自适应控制、牵制控制的方法得到了可以应用在无时滞或单边的系统中的控制方法。并且去掉了传统间歇控制中控制宽度和时延上需要满足的条件,使得应用范围更广,并且书中还通过仿真证明了控制器的有效性。
5. 总结与展望
目前对于复杂网络同步控制的研究已经进入到了一个比较成熟的时期。针对复杂网络的研究成果越来越多,一些成果也可以被应用到实际生活当中。但是对于复杂网络同步控制的研究还不尽完善,有许多领域还需要通过不断地研究来完善。
从网络拓扑结构的模型建立方面来说从最早的规则网络模型到现在的无标度网络模型,随着模型的不断完善无标度网络模型已经可以有效的反映现实生活中许多复杂网络的数字特性,但是模型的建立是一种简化的研究对象相比于现实生活中见到的真是网络只是具备其部分本质特征,而对于具体网络收到的环境等多方面因素引起的个性化特点不能准确地反映,因此在实际应用当中会受到一定的限制。因此建立可以反应某一类型实际问题的网络模型也是值得研究的。
从控制手段的方面来说现在单一的控制方法其相关的理论研究与仿真试验已经相对成熟,因此人们着手于研究将几种控制手段相结合的控制方法,如脉冲牵制控制、间歇牵制控制、自适应牵制控制等。是否能将各种控制手段进行有效的集成获得个好的控制手段并应用到实际工程当中也是对于复杂网络同步控制研究的一个挑战。
针对牵制控制这种控制手段来说经过之前学者的大量研究也逐渐走向成熟,如不同拓扑结构下的稳定条件、牵制控制在复杂网络控制中的适用条件等都有系统的介绍。但是就牵制控制而言也存在着许多值得我们研究探索的领域。在许多文献中都提到牵制控制是选取部分节点施加控制。具体选取多少节点并没有详细的介绍,网络的拓扑结构及外部扰动等因素是否会影响节点选取的数量。而且对于节点选取的规则大多是笼统的介绍,目前一般采取的是前文中提到的特定节点牵制控制,如果能进一步完善节点的选取规则对于实际应用也有着很大的帮助,因此牵制控制的节点选取方面也具有一定的研究空间。
虽然复杂网络同步控制的研究已经发展到了一定的高度,但是在许多方面还有待于开发研究,还有很多有价值的问题等待着人们去发现探索。
基金项目
辽宁省自然科学基金(20170540769);辽宁“百千万人才工程”培养经费资助(辽百千万立项[2017]76号);沈阳建筑大学学科涵有计划项目(XKHY-79);辽宁省博士启动基金(20170520283)。
文章引用
贾 兴,孙海义. 复杂网络同步控制方法研究综述
Review of Synchronous Control Methods in Complex Networks[J]. 动力系统与控制, 2018, 07(04): 318-327. https://doi.org/10.12677/DSC.2018.74036
参考文献
- 1. 张峥, 朱炫颖. 复杂网络同步控制的研究进展[J]. 信息与控制, 2017, 46(1): 103-112.
- 2. 陈关荣. 复杂网络及其新近研究进展简介[J]. 力学进展, 2008(38): 653-622.
- 3. 项林英. 复杂动态网络的建模、分析与控制研究综述[J]. 自然科学进展, 2006(16): 1543-1551.
- 4. 陈关荣. 复杂动态网络环境下控制理论遇到的问题与挑战[J]. 自动化学报,2013(39): 312-321.
- 5. 巴曙松, 左伟, 朱元倩. 金融网络及传染对金融稳定的影响[J]. 财经问题研究, 2013(2): 3-11.
- 6. Erdős, P. and Rényi, A. (2011) On the Evolution of Random Graphs. Transactions of the American Mathematical Society, 286, 257-274.
- 7. 徐吉. 基于牵制控制的复杂网络同步及其应用[D]. 南京邮电大学, 2014.
- 8. 傅新楚, 朱杰. 复杂网络的同步能力与传播动力学性态[C]//全国非线性动力学和运动稳定性学术会议, 2011.
- 9. Watts, D.J. and Strogatz, S.H. (1998) Collective Dynamics of “Small-World” Networks. Nature, 393, 440-442.
https://doi.org/10.1038/30918 - 10. Barabási, A.L. and Albert, R. (1999) Emergence of Scaling in Random Networks. Science, 286, 509-512.
- 11. 陈娟,陆君安. 复杂网络同步态与孤立节点解的关系[J]. 自动化学报, 2013(39): 2111-2120.
- 12. 汪小帆, 苏厚胜. 复杂动态网络控制研究进展[J]. 力学进展, 2008, 38(6): 751-765.
- 13. Wang, X.F. and Chen, G. (2002) Pinning Control of Scale-Free Dynamical Networks. Physica A Statistical Mechanics & Its Applications, 310, 521-531.
https://doi.org/10.1016/S0378-4371(02)00772-0 - 14. Fan, Z. and Chen, G. (2005) Pinning Control of Scale-Free Complex Networks. IEEE International Symposium on Circuits and Systems, 1, 284-287.
- 15. 吴晔, 肖井华, 占萌. 强耦合混沌系统中的近似同步[J]. 物理学报, 2007, 56(9): 5119-5123.
- 16. Wang, X.F. and Chen, G.R. (2002) Synchronization in Scale-Free Dynamical Networks: Robustness and Fragility. IEEE Transactions on Circuits and Systems I: Fundamental Theory and Applications, 49, 54-62.
https://doi.org/10.1109/81.974874 - 17. Wang, X.F. and Chen, G.R. (2002) Synchronization in Small-World Dynamical Net-works. International Journal of Bifurcation and Chaos, 12, 187-192.
https://doi.org/10.1142/S0218127402004292 - 18. Barahona, M. and Pecora, L.M. (2002) Synchronization in Small-World Systems. Physical Review Letters, 89, Article ID: 054101.
https://doi.org/10.1103/PhysRevLett.89.054101 - 19. Stefánski, A., Perlikowski, P. and Kapitaniak, T. (2007) Ragged Synchronizability of Coupled Oscillators. Physical Review E, 75, Article ID: 016210.
https://doi.org/10.1103/PhysRevE.75.016210 - 20. Duan, Z.S., Chen, G.R. and Huang, L. (2009) Disconnected Synchronized Regions of Complex Dynamical Networks. IEEE Transactions on Automatic Control, 54, 845-849.
https://doi.org/10.1109/TAC.2008.2009690 - 21. 夏青. 复杂动态网络的脉冲控制研究[D]: [硕士学位论文]. 南京: 南京邮电大学, 2012.
- 22. Yang, T. (1994) Impulsive Control. IEEE Transaction on Automatic Control, 44, 1081-1083.
- 23. 韦琳娜. 几类连续时间和离散时间脉冲系统稳定与镇定研究[D]: [博士学位论文]. 广州市: 华南理工大学, 2015.
- 24. Lakshmikantham, V., Bainov, D.D. and Simeonov, P.S. (2006) Theory of Impulsive Delay Difference Equation. Applied Mathematics and Computation, 181, 65-72.
https://doi.org/10.1016/j.amc.2006.01.015 - 25. Shen, J.H. and Yan, J.R. (1998) Razumikhin Type Stability Theorems for Impulsive Functional Differential Equations. Nonlinear Analysis, 33, 563-576.
https://doi.org/10.1016/S0362-546X(97)00565-8 - 26. Liu, X. and Zhang, K. (2016) Synchronization of Linear Dynamical Networks on Time Scales: Pinning Control via Delayed Impulses. Automatica, 72, 147-152.
https://doi.org/10.1016/j.automatica.2016.06.001 - 27. 冯纯伯. 关于自适应控制理论的发展[J]. 机器人, 1982, 4(2): 14-19.
- 28. 王劲毅. 基于若干控制策略的几类复杂网络同步研究[D]: [博士学位论文]. 深圳: 深圳大学, 2015.
- 29. 任红卫, 邓飞其. 随机复杂网络同步控制研究进展综述[J]. 控制理论与应用, 2017(10): 1261-1274.
- 30. 李宁, 孙海义, 孙常春. 复杂动力网络的同步分析与控制[M]. 北京: 人民邮电出版社, 2017: 147-168.
NOTES
*通讯作者。