 Journal of Image and Signal Processing 图像与信号处理, 2013, 2, 1-7 http://dx.doi.org/10.12677/jisp.2013.21001 Published Online January 2013 (http://www.hanspub.org/journal/jisp.html) Image Denoising by Zernike-Moment-Similarity Collaborative Filtering* Xiuchun Xiao1,2, Jianhuang Lai1 1School of Information Science and Technology, Sun Yat-sen University, Guangzhou 2College of Information, Guangdong Ocean University, Zhanjiang Email: stsljh@mail.sysu.edu.cn, springxxc@163.com Received: Oct. 22nd, 2012; revised: Nov. 6th, 2012; accepted: Nov. 15th, 2012 Abstract: Because similarity function defined in non-local means filter is subject to image noise, it cannot robustly represent the real similarity between pixels. Zernike moments are good statistics of the pixels in image patch, and have rotation-invariant feature, so they can be utilized to describe image feature while resistance to noise. In this paper, Zernike-moment-similarity is defined according to the difference of Zernike moments instead of pixel intensity, and then the intensity of the processed pixel is estimated by weighting the intensities of the local window according to the collaborative Zernike-moment-similarity. Simulation experiment results and analysis demonstrate that the presented algorithm can achieve better performance and higher PSNR than the current algorithms which directly adopting inten- sity difference as its similarity function. Keywords: Image Denoising; Multilateral Filtering; Non-Local Means Filtering; Similarity Measure; Zernike Moments 基于 Zernike 矩相似度联合的图像滤波* 肖秀春 1,2,赖剑煌 1 1中山大学信息科学与技术学院,广州 2广东海洋大学信息学院,湛江 Email: stsljh@mail.sysu.edu.cn, springxxc@163.com 收稿日期:2012 年10 月22日;修回日期:2012 年11 月6日;录用日期:2012年11月15 日 摘 要:非局域均值滤波(non-local means filtering, NLMF)采用图像块间灰度差测度像素间相似性,由于灰度差 易受噪声影响,这种相似性测度缺乏鲁棒性。图像块的Zernike 矩是块内像素灰度的统计量,且具有旋转无关特 性,能在抑制噪声的情况下较好地描述图像块特征。由图像块的各阶 Zernike 矩差代替灰度差可定义 Zernike 矩 相似度;联合各阶 Zernike 矩相似度经加权平均可估计出所处理像素的灰度。仿真实验及分析表明文中算法相比 直接采用灰度差定义相似度的算法,能更好地去除噪声,获得更高的峰值信噪比(PSNR)。 关键词:图像去噪;多边滤波;非局域均值滤波;相似性测度;Zernike 矩 1. 引言 受拍摄对象的相对运动、所处光学环境以及摄取 设备精度等条件的限制,数字图像在获取过程中不可 避免地会导致噪声的产生[1]。然而,与图像分析相关 的诸多应用如图像分割、图像检索、边缘提取等,通 常需要去除噪声的影响以获得更为鲁棒的分析效果 [2]。因此,为了尽可能减少噪声对于后续图像分析的 影响,探索有效的图像去噪方法成为图像处理研究中 的重要课题。 图像双边滤波是一种简单、非迭代、局部的图像 去噪算法,它的思想最早由 Aurich 等[3]、Smith 等[4]、 *基金项目:本文受国家自然科学基金(61173084)资助。 Copyright © 2013 Hanspub 1  基于 Zernike 矩相似度联合的图像滤波 Tomasi 等[5]分别独立提出。该算法将图像中两像素欧 氏距离的高斯函数定义为空间临近度;同时,将两像 素灰度差的高斯函数作为其相似性测度。显然,两像 素距离越近,其空间临近度越大;灰度差越小,其相 似度越高。通过联合空间临近度和像素的相似度可定 义权函数,对邻域内像素灰度加权平均估计出所处理 像素的灰度。相比均值滤波、高斯滤波、中值滤波等 其他传统空间域图像去噪算法,双边滤波能够在较好 地保持图像的特征的前提下,更有效地去除噪声[5]。 该算法提出后逐渐受到广泛重视且在图像去噪和 3D Mesh 去噪[6,7]等方面有较多的应用。但由于其采用受 噪声污染的灰度差直接定义相似度,因此鲁棒性尚需 改善。近年来,研究人员对该算法理论的思想进行了 较深入的研究,提出了一些有效改进,如 Francis 等[8], 张鑫等[9],肖秀春等[1]分别提出了双边中值滤波、三 边滤波、次序统计量双边滤波等。 Buades 等[10,11]提出的非局域均值滤波是在双边 滤波的基础上发展起来的空间域图像去噪算法。它以 当前像素为中心,定义大小固定的图像块,采用图像 块间灰度差的加权高斯函数测度其中心像素间相似 性,然后对邻域内像素灰度加权平均来估计所处理像 素的灰度。由于该算法实际利用了图像中的纹理冗余 以及结构信息,因此它非常适合于处理纹理图像,且 其滤波后的残差图像更接近高斯噪声图像,因而对图 像边缘等细节特征损失较少。但是,该算法在以下两 个方面不够完善:一方面,该算法直接采用灰度差测 度相似性,而灰度差受噪声影响较大,故这种灰度相 似性测度的鲁棒性可进一步改善;另一方面,该算法 逐像素地计算图像块相似度,存在计算复杂度较高的 缺点。Tasdizen[12],Orchard 等[13]分别采用主成分分析 和奇异值分解等方法改善了相似度的测度方法,提高 了图像滤波效果。Zimmer 等[14]将图像块相应地作一 定角度的旋转,以期获得最佳匹配角度,然后再计算 图像块相似度,这种改进能更好地保持图像细节特 征。Liu等[15]结合 Laplacian 图像金字塔和快速傅立叶 变换计算像素之间的相似度,提出了一种鲁棒、快速 的实现算法。 文中主要对非局域均值滤波中的相似性测度提 出了改进方法。与非局域均值滤波不同的是,文中对 像素之间的相似性测度采用 Zernike矩差而不是直接 采用图像块灰度差。由于噪声图像中像素的灰度受到 污染,灰度差为灰度的差分,亦必受到污染,直接采 用灰度差定义两个像素的相似性,这种相似性对噪声 敏感,而 Zernike 矩为图像中像素灰度统计特性,受 噪声影响较小,又能较好描述图像像素灰度特征,因 此采用 Zernike矩差测度像素之间相似性的优点之一 就是能较好地抑制噪声影响。文中通过仿真实验表明 该算法确实能有效提高去噪性能。 另外,图像的每一个 Zernike 矩都具有旋转不变 特性,且都只能描述图像的某些方面的特征,故将其 联合起来才能描述图像的整体特征。相应地,将图像 的多个 Zernike 矩差定义的各 Zernike 矩相似度联合起 来(通过乘积形式)才能更准确地描述像素之间的相似 性,同时,该联合的相似度也就具有了旋转不变性, 这将有利于准确找到具有相同灰度分布但方向不同 的图像块。文中通过仿真实验及分析表明验证了这种 特性。 2. 非局域均值滤波理论 众所周知,两像素之间的相似性可以通过某种距 离或者联合某些距离来测度,利用高斯函数定义其为 权值对邻域内像素的灰度进行加权平均可估计所处 理像素的灰度。非局域均值滤波采用图像块之间的灰 度差代替双边滤波中单一像素之间的灰度差定义权 值,较好地改善了图像滤波的效果。 一般地,对于灰度数字图像,可以设计非局域均 值滤波器为, nlmean nlmean , ˆ, p p qN qN wpquq vp wpq (1) 由式(1)中 ˆ vp的定义,可知非局域均值滤波本 质是对所处理像素 p的邻域 Np内所有像素q之灰度的 加权平均。式中, ˆ vp为该像素滤波后的灰度、即为 纯净图像灰度 vp qN 的估计值,Np为像素 p的一定范 围邻域,q为该邻域中的任意像素,像素 q滤波 前的灰度, uq mean ,wp q nl p 为归一化因子, nlmean ,wpq 为邻域 Np内像素 q在滤波时的权函数, 定义为, nlmean 2 1 ,exp , 2 wpq pq h 式中,h为滤波器参数,为像素 p、q各自所 在图像块中对应像素之间的加权灰度差平方的和值, ,pq Copyright © 2013 Hanspub 2  基于 Zernike 矩相似度联合的图像滤波 Copyright © 2013 Hanspub 3 定义为: 2 2 2 ,2 , 1 exp 2 pq rN sN pq rsur us 式中,Np、Nq分别为以像素 p、q为中心的图像块, 像素 r、s分别位于图像块 Np、Nq内,且处于两个图 像块中相对应的位置, 2 rp为图像块 Np中像素 r 与中心像素 p之间的欧氏距离(注:也即图像块 Np中 像素 s与中心像素 q之间的欧氏距离), 为距离衰减 参数;、分别为像素 r、s的灰度。 ur us 由式(1)中 ˆ vp的定义,可知非局域均值滤波本 质是对邻域内像素灰度的加权平均。式中直接采用图 像块灰度差定义相似度,但由于灰度受到噪声直接影 响,因此,这种灰度相似性测度的鲁棒性尚需进一步 改善。 3. Zernike矩相似度联合滤波 如前所述,直接使用单一像素或图像块的灰度差 测度像素之间相似性,可能导致较严重误差。Zernike 矩在图像描述、识别、检索等方面应用广泛;图像的 Zernike 矩作为一种统计量,其受噪声影响小。因此, 可以由像素所在图像块的各阶 Zernike矩差代替灰度 差测度像素之间的相似性,联合各阶Zernike 矩相似 度可定义邻域内各像素的权值,通过加权平均实现滤 波。 3.1. 图像 Zernike 矩 图像矩是图像的重要特征,设图像的灰度函数为 ,则其 m + n阶矩 的一般形式为, ,uxy mn ,,dd,0,1,2, mn mn xy xyuxyxy mn (2) 对于数字图像 ,式(2)可写为离散形式, ,uxy ,,,0,1,2, mn mn xy Axyuxymn (3) 式(2)、(3)中, , mn x y称为矩的核函数或基集。若 采用最简单的二元幂多项式 ,mn mn x yxy作为基 集定义图像矩 mn A ,称为几何矩。但该基集 mn x y是 完备非正交的,因此,几何矩存在信息冗余。为解决 信息冗余问题,可以采用正交多项式定义图像矩。 1934 年,荷兰物理学家 Zernike 提出了一组定义 在极坐标系下单位圆上的正交完备复多项式集,其定 义为, ,cos,sin exp mn mnmn VxyVrrRrjn 其中, mn Rr为正交径向多项式,定义为, 2 2 0 ! 122 !! 22 mn mn sms s Rr ms r msnmsn s ! 其中, 0,1, 2,m ;0nm ;且mn为偶数。 由正交复 Zernike 多项式 可定义数字图 像 , mn Vxy ,uxy的Zernike 矩, 22 1,, 1 π 1expcos, sin1 π mn mn xy mn r n ZVxyuxyxy m R rinurrr (4) 其中, mn Z 即图像的 m阶n重Zernike 矩,*表示共轭 复数, ,r 为单位圆内像素的直角坐标 , x y对应的 极坐标。 由于 Zernike 多项式是单位圆上的正交完备复多 项式集,因此 Zernike 矩具有良好的图像表达能力。 另外,式(4)也表明,Zernike 矩实质为统计特征,因 而具有对噪声不敏感的特性。 3.2. 图像 Zernike 矩相似度联合滤波 前述 Zernike 矩的定义针对整幅图像;显然,对 于数字图像 ,uxy中的图像块,也可以类似地定义其 m阶n重Zernike 矩mn Z ;另外,为了叙述方便,在不 至于混淆的情况下,我们也称mn Z 为图像块中心像素 的m阶n重Zernike 矩。 另外,需要特别指出的是,Zernike矩定义在单位 圆上,而实际数字图像仅容易得到正方形图像块;为 此,可以先将正方形图像块映射到边长为 2(注:单位 圆的直径为 2)的正方形内,然后采用圆盘掩码对该正 方形进行剪切得到单位圆,最后利用式(4)计算Zernike 矩mn Z 。为了降低计算量,文中采用大小为 7 × 7 的图 像块计算像素的各阶 Zernike 矩mn Z 。 及非局域均值滤波中像素 度定义, Zernike 矩相似 类似于双边滤波 相似 度 , mn wpq可定义为,  基于 Zernike 矩相似度联合的图像滤波 2 2 1 expq , mnmn mn mn wpZq Zp h (5) 其中,称为像素 p与q之间的 m阶n重 , mn wpq 矩相似度Zernike;mn Z 为Zernike 矩, ,0,1,2,,0 , mn Zm mmn为偶 n数 ,即, ; 00 11 2022 ,,,, mn ZZZZZ mn Z q mn Z p分和 别为以像素 q,p为中心的图像块的 m阶重 Zern 各阶 nike 矩的模值;mn h为m阶n重Zernike 矩滤波参数,其 取值大小控制 Zernike 矩相似度的贡献,文中取 mn mn h ,其中 mn 为图像所有像素的m阶n重 标准差 为根据经验设置的常数。显然, 当各阶 Zernike 矩相似度均较大时,像素之间灰度的 相似性较大。因此,联合像素各阶Zernike 矩相似度, 可设计如下滤波器, Zernike 矩的 , , , , ˆ , ,|0,1, 2,, 0,iseven p p qN mn mn qN mn mn wpquq vp wpq mn mnmmn (6) 由式(6)中的定义,可知新的滤波器仍是对邻域 ˆ vp p N内所有像素灰度的加权平均。但其权函数采用图 的Zernike矩差而不是直接采用其灰度差定义。 式中, 表示连乘运算,表示(m, n)的取值集,在 文中的实际应用中可取 ,1, 2, 3m,因此有 像块 0 2, 0,2, 2 ,|0,0,1,1 ,,3,1 ,3,3mn 。 值得指出的是,由式(4)可知,任一图像块旋转角 度 前后的 Zernike 矩模值mn Z 和mn Z 之间存在如下 关系: exp in mn mnmn Z ZZ 前式表明,图像块旋转前后其Zernike 矩的模值 不变 3.3. 灰度相似性测度准确性对比 双边滤波、非局域均值滤波等空间域滤波算法依 据像 证文中算法相对传统非局域均值滤波能 具有 相似 为了进一步比较探讨文中算法对实际图像的滤 波性 ,即图像 Zernike矩具有旋转不变性[16],这一特 性非常有用。 素之间的相似度确定其加权权值,因此,相似性 测度的准确性决定了其滤波性能。非局域均值滤波采 用像素所在图像块灰度差测度像素间的相似性,由于 噪声的影响,所计算的相似性难以准确地测度像素之 间的相似程度。另一方面,图像块的各阶Zernike 矩 为块内像素灰度的统计特性,这在一定程度上了抑制 噪声的影响,因而采用图像块的各阶Zernike 矩差代 替图像块的灰度差测度其灰度相似性,具有较低噪声 敏感性。 为了验 更良好的相似性,我们设计了图 1(a)所示三幅人 工图像。这三幅人工图像分别代表了图像中存在曲线 边、直线边和反转曲线边的情况,用来测试两种算法 在各种情况下的准确性及鲁棒性。图1(b)为对应添加 高斯白噪声图像。分别应用非局域均值滤波和文中算 法对图 1(a)、(b)中各红色标记像素计算其与其他像素 之间的相似度(为便于显示,将计算得到的相似度值按 比例变换到 0~255 之间,相似度高则显示为白色)。 图1(c)、(d)为采用非局域均值滤波算法时测度的 度分布,(e)、(f)为采用文中算法测度的对应相似 度分布。观察对比无噪声情况下的两种算法的测度结 果即图 1(c)、(e)可知,非局域均值滤波仅能检测到在 同一直线上的“边”像素,而文中算法能更准确地检 测到图像中所有与其相似的“边”像素。进一步地, 观察对比噪声情况下的测度结果对比即图 1(d)、(f)可 知,非局域均值滤波算法计算的相似度呈现大片区域 显示为泛白区域(见图 1(d)),而文中算法在噪声情况 下仍能检测出与标记点相似的所有“边”像素。这表 明,文中算法相比非局域均值滤波能更为鲁棒地测度 像素之间的相似度。 4. 实验及分析 能,采用标准测试图像中添加一定的高斯白噪声 作为实验噪声图像,噪声模型定义为, uv (7) 其中, 为噪声图像灰度矩阵 u ,v为标准测试图像灰 度矩阵, 为零均值、方差为 2 n 的高斯白噪声,标 准差 n 的不同取值代表了不同强 噪声。 另外,可采用峰值信噪比(PSNR)作为对 度 算法滤波 性能的定量评价准则,峰值信噪比定义为, 2 255 2 ,, 11 PSNR10lgdB 1ˆ MN ij ij ii vv M N Copyright © 2013 Hanspub 4  基于 Zernike 矩相似度联合的图像滤波 Copyright © 2013 Hanspub 5 (a) (b) (c) (d) (e) (f) Figure 1. Comparison of the similarity distribution used to the label pixel in the clean/noisy images: (a), (b) Clean/noisy images with label pixel; (c), (d) Similarity measur e results of non-local means; (e), (f) Similarity measure results of the proposed algorithm 图1. 在无噪 /加噪情况下对标记点测度的相似度分布对比:(a)、(b) 无噪/加噪图像;(c)、(d) NLMeans算法的相似度测度结果;(e)、(f) 文 中算法的相似度测度结果 其中,v的定义与式(7)相同, 为滤波结果图像,M 和N分别为图像矩阵的行数和列数。 我们在不同噪声水平下应用双边滤波(BF)、非局 域均值滤波(NLMF)、基于次序统计量相似度的双边 滤波(OSSBF)和文中算法对实验噪声图像进行去噪处 理,然后对去噪结果图像(图2)及其峰值信噪比数据 (表1)进行对比和分析。值得指出的是,在本节仿真实 验中,各算法的搜索邻域窗口均取为 21 × 21的图像 块;非局域均值滤波和文中算法采用大小为 7 × 7的 图像块计算图像块相似度或各阶 Zernike矩;双边滤 波[5] 的滤波参数(参数定义可参见文献[5])分别为 ˆ v 25 r 和3 d ;非局域均值滤波[11] 参数分别为 n (其中n 为噪声强度)和,基于次序统计 边滤 的参数(参数定 参见文献[11]) 分 3h 义可量的双 别r 波[1] 20 和d5 ,文 波器参数为 图2(a)为带高斯白噪声标准方差 中算法滤 1.5 mn h。 20 n 的Lena、 Peppers、Boat 标准测试噪声图像;图 2(b)~(e)显示了 采用前述各算法对噪声灰度标准图像进行滤波后的 图像结果对比。仔细观察和对比图 2(b)~(e)中图像去 噪结果,可以看到,图 2(e)所展示的基于 Zernike 矩 相似度联合的图像滤波算法对三种测试图像效果均 较好。 为进一步定量地比较文中算法的滤波特性,我们 在不同噪声水平下应用双边滤波(BF)、非局域均值滤 波(NLMF) 、基于次序统计量相似度的双边滤波 (OSSBF)和文中算法测试了大量标准测试图像滤波后 的峰值信噪比(PSNR),但限于文章篇幅,我们仅给出 对部分最常用的标准测试图像的PSNR 结果的对比数 据如表 1所示(表示将性能最好的两种算法 PSNR 值用 加粗的形式给出)。对比和分析表 1中定量评价指标 PSNR 数据可知,文中算法相比其他滤波算法在不同 噪声水平中大都获得了较高的峰值信噪比。 5. 讨论与结论 通常,空间域图像滤波本质是对局部邻域内的像 素灰度进行加权平均来估计当前像素灰度。一般地, 我们期望与当前像素灰度的理想值相近(文中称为相  基于 Zernike 矩相似度联合的图像滤波 (a) (b) (c) (d) n cal based bilateral filtering; (e) Proposed algorithm (e) 2. arison of restoration results fo standard test images with σ = 20 of Gaussian white noise: (a) Noisy images; (b) atisti 的滤波结果对比:(a) 噪声图像;(b) 双边滤波;(c) 非局域均值滤波; 双边滤波;(e) 文中算法 FigureCom pr different Bilateral filtering; (c) Non-local means; (d) Order st 图2. 对高斯白噪声 σn = 20的标准测试图像 Lena、Peppers、Boat (d) 次序统计量相似度 Copyright © 2013 Hanspub 6 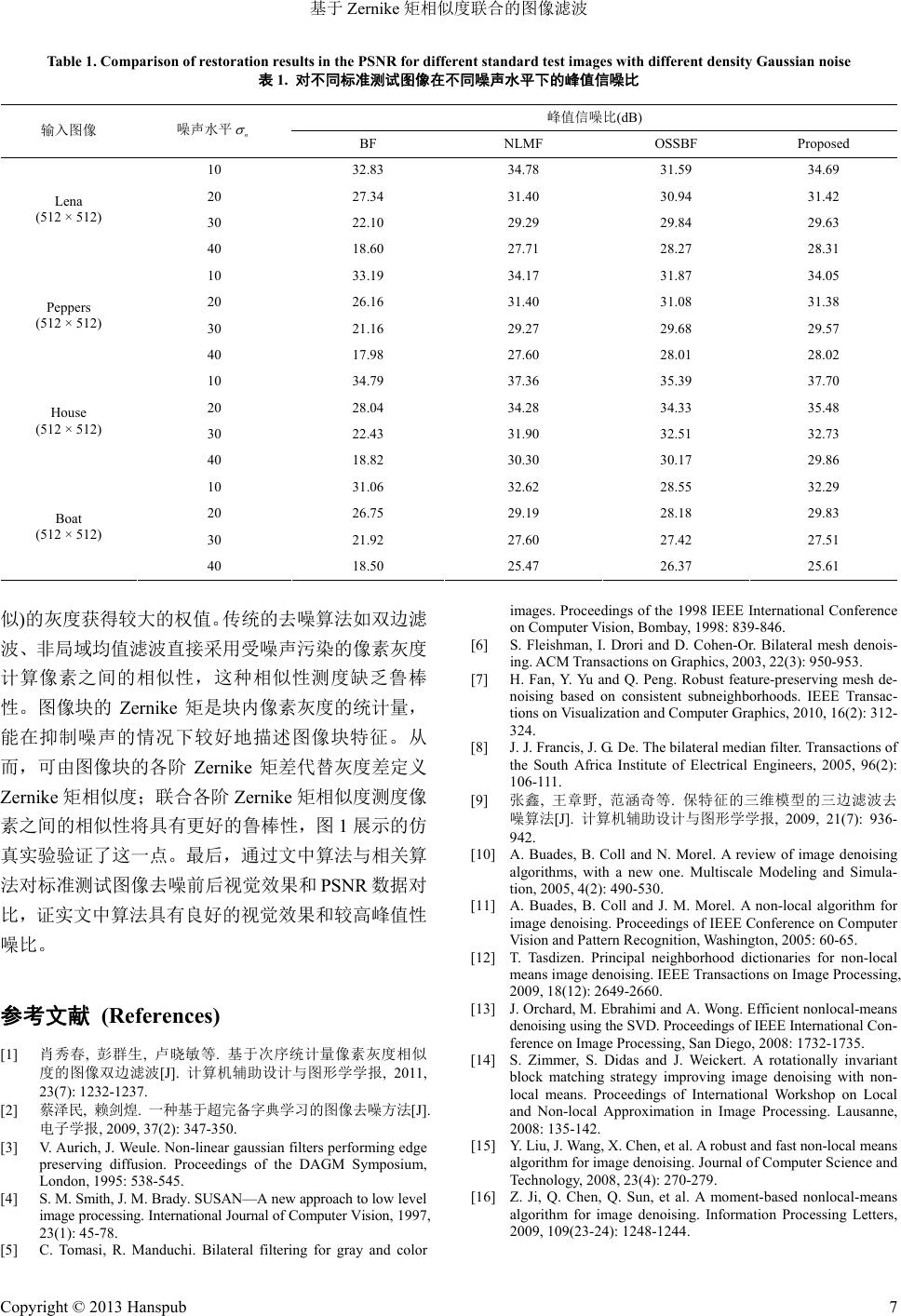 基于 Zernike 矩相似度联合的图像滤波 Table 1. Comparison of restoration results in the PSNR for different standard test images with different density Gaussian noise 表1. 对不同标准测试图像在不同噪声水平下的峰值信噪比 峰值信噪比(dB) n 输入图像 噪声水平 BF NLMF OSSBF Proposed 10 32.83 34.78 31.59 34.69 20 27.34 31.40 30.94 31.42 30 22.10 29.2929.84 29.63 Lena (512 × 512) 40 18.60 27.7128.27 28.31 10 33.19 34.17 31.87 34.05 20 26.16 31.40 31.08 31.38 30 21.16 29.27 29.68 29.57 Peppers (512 × 512) 40 17.98 27.60 28.01 28.02 10 34.79 37.36 35.39 37.70 20 28.04 34.28 34.33 35.48 30 22.43 31.90 32.51 32.73 House (512 × 512) 40 18.82 30.30 30.17 29.86 10 31.06 32.62 28.55 32.29 20 26.75 29.19 28.18 29.83 30 21.92 27.60 27.42 27.51 Boat (512 × 512) 40 18.50 25.47 26.37 25.61 似)的灰度获得较大的权值。传统的去噪算法如双边滤 波、非局域均值滤波直接采用受噪声污染的像素灰度 计算像素之间的相似性,这种相似性测度缺乏鲁棒 性。图像块的 Zernike 矩是块内像素灰度的统计量, 能在抑制噪声的情况下较好地描述图像块特征。从 而,可由图像块的各阶 Zernike 矩差代替灰度差定义 Zernike 矩相似度;联合各阶 Zernike 矩相似度测度像 素之间的相似性将具有更好的鲁棒性,图 1展示的仿 真实验验证了这一点。最后,通过文中算法与相关算 法对标准测试图像去噪前后视觉效果和PSNR 数据对 比,证实文中算法具有良好的视觉效果和较高峰值性 噪比。 参考文献 (References) [1] 肖秀春, 彭群生, 卢晓敏等. 基于次序统计量像素灰度相似 度的图像双边滤波[J]. 计算机辅助设计与图形学学报, 2011, 23(7): 1232-1237. [2] 蔡泽民, 赖剑煌. 一种基于超完备字典学习的图像去噪方法[J]. 电子学报, 2009, 37(2): 347-350. [3] V. Aurich, J. Weule. Non-linear gaussian filters performing edge preserving diffusion. Proceedings of the DAGM Symposium, London, 1995: 538-545. [4] image proc [5] C. Tomasi, R. Manduchi. Bilateral filteri images. Proceedings of the 1998 IEEE International Conference on Computer Vision, Bombay, 1998: 839-846. [6] S. Fleishman, I. Drori and D. Cohen-Or. Bilateral mesh denois- ing. ACM Transactions on Graphics, 2003, 22(3): 950-953. [7] H. Fan, Y. Yu and Q. Peng. Robust feature-preserving mesh de- noising based on consistent subneighoods. IEEE Transac- tions on Visualization and Computer Graphics, 2010, 16(2): 312- 324. [8] J. J. Francis, J. G. De. The bilateral median filter. Transactions of the South Africa Institute of Electrical Engineers, 2005, 96(2): 106-111. [9] 张鑫, 王章野, 范涵奇等. 保特征的三维模型的三边滤波去 噪算法[J]. 计算机辅助设计与图形学学报, 2009, 21(7): 936- 942. [10] A. Buades, B. Coll and N. Morel. A review of image denoising algorithms, with a new one. Multiscale Modeling and Simula- tion, 2005, 4(2): 490-530. [11] A. Buades, B. Coll and J. M. Morel. A non-local algorithm for image denoising. Proceedings of IEEE Conference on Computer Vision and Pattern Recognition, Washington, 2005: 60-65. [12] T. Tasdizen. Principal neighborhood dictionaries for non-local means image denoising. IEEE Transactions on Image Processing, 2009, 18(12): 2649-2660. [13] J. Orchard, M. Ebrahimi and A. Wong. Efficient nonlocal-means denoising using the SVD. Proceedings of IEEE International Con- ference on Image Processing, San Diego, 2008: 1732-1735. [14] S. Zimmer, S. Didas and J. Weickert. A rotationally invariant block matching strategy improving image denoising with non- local means. Proceedings of International Workshop on Local and Non-local Approximation in Image Processing. Lausanne, 2008: 135-142. [15] Y. Li. Wang, X. Chen, et al. A robust and fast non-local means algorithm for image denoising. Journal of Computer Science and Technology, 2008, 23(4): 270-279. s g Letters, S. M. Smith, J. M. Brady. SUSAN—A new approach to low level essing. International Journal of Computer Vision, 1997, [16] Z. Ji, Q. Chen, Q. Sun, et al. A moment-based nonlocal-mean algorithm for image denoising. Information Processin 23(1): 45-78. ng for gray and color 2009, 109(23-24): 1248-1244. hbor u, J Copyright © 2013 Hanspub 7 |