 Hans Journal of Wireless Communications 无线通信, 2013, 3, 13-17 http://dx.doi.org/10.12677/hjwc.2013.31003 Published Online February 2013 (http://www.hanspub.org/journal/hjwc.html) Array Antenna Mutual Coupling Analysis —Mutual Coupling Correction Techniques Based on Induced Electromotive Method of Uniform Circular Array Antennas Yanzhi Fang College of Electronic Science and Engineering, Nanjing University of Posts and Telecommunication, Nanjing Email: fyzycb@163.com Received: Dec. 25th, 2012; revised: Jan. 7th, 2013; accepted: Jan. 28th, 2013 Abstract: Mutual coupling effects lead to the coupling energy vector between antenna units changing with the scan angle. For antenna array mutual coupling analysis, signal direction can be correctly estimated by solving the mutual coupling matrix and putting mutual coupling matrix solution into the wave direction of arrival estimation correction formulas combined equivalent network knowledge and induced electromotive method. The simulation results show that signal direction can be correctly estimated and computation is small. Keywords: Array Antenna; Mutual Coupling; Wave Direction of Arrival Estimation 阵列天线的互耦分析 —基于感应电动势法的均匀圆阵互耦校正技术 方焱枝 南京邮电大学,电子科学与工程学院,南京 Email: fyzycb@163.com 收稿日期:2012 年12 月25日;修回日期:2013 年1月7日;录用日期:2013年1月28 日 摘 要:互耦效应导致阵列天线单元间耦合能量的矢量和随扫描角而变化,本文结合等效网络和感应电动势法, 通过求出互阻抗求解互耦系数实现互耦误差的校正,仿真结果表明,这种技术可以正确的估计来波方向,且计 算量较小。 关键词:阵列天线;互耦;波达方向 1. 引言 空间谱估计(DOA),是一种空域处理技术,主要 目的是估计信号的空域参数或信源位置[1],作为阵列 信号处理中的一个重要分支,在最近几十年得到迅速 发展,其应用涉及雷达,通信,声纳等领域。以前发 表的文献往往把注意力都集中在提高算法的效率或 是提高算法的精度的研究,这些算法的前提是假设各 阵元能独立工作。然而,实际中,各阵元之间是互相 影响的,所以互耦效应是阵列天线的分析和设计必须 考虑的因素[2],利用一定数量的校正信源,基于结构 最小二乘法的思想,通过循环迭代的方式实现了互耦 误差的校正,该方法需要较多数量的辅助信源且计算 量大[3]。利用存在互耦时的阵列流型与理想阵列流型 的偏差构造罚函数,通过迭代寻优实现了互耦误差的 估计和校正,该方法能推广应用于一般线性阵列,但 是其需要迭代求解,每次迭代计算量也较大。近年来 也有许多新的算法提出[4],提出一种基于均匀圆阵的 互耦误差校正方法,它只需要一个方向未知的辅助校 正信源,通过构造代价函数并对其优化求解得到互耦 Copyright © 2013 Hanspub 13  阵列天线的互耦分析—基于感应电动势法的均匀圆阵互耦校正技术 矩阵估计值,然后通过谱峰搜索估计校正信源到达 角,迭代实现互耦参数与 DOA 的估计。上面的这些 方法要么计算量大,要么需要辅助校正信源,本文结 合等效网络和感应电动势势法,通过求出互阻抗求解 互耦系数实现互耦误差的校正。 2. 互耦的空间谱估计的影响 2.1. 空间谱估计算法—MUSIC 算法[5 ] 假设阵列由 M 个阵元组成,有 个不相 干的信号源位于远场,DOA 分别为 PP M 12 ,,, P ,第 个阵元接收信号 l 1, 2,,lM 0 1 p lii il x tawstn t (1) 其中 i s t l nt 表示第 个阵元接收到的来自于第 个源的 信号, 为零均值、方差为 li 2 的加性噪声,源信 号和噪声信号不相关 01 020 0ee e ii jw jwjw i aw Mi (2) 称为导向矢量,根据(1)可以写出阵列的接收信号矢量 表达式: X tAStNt (3) 其中 可以得到(2) 的协方差矩阵: 10 200p Aa aa 2 HHH HH SNS R EXtX tAESSAENN AR ARAR AI H (4) 由数学知识可以将 R写成如下: H H s ss NNN RU UUU (5) S U对应信号子空间, N U对应噪声子空间,R进行特 征分解,得到 N U, N U为M-P 个小特征值对应的特 征向量组成的矩阵 1HH iiNN PaUUa i (6) 对谱函数进行谱峰搜索,所得P的p个最大值所对应 的 值就是来波信号的到达角。 2.2. 互耦模型 依据不同的误差参数,阵列误差可分为阵元互 耦、阵元幅相、阵元位置等几种误差类型。本节将主 要分析天线阵列互耦误差及其模型。 对于 M 元阵列,将其等效为线性双向 1 M 端口 网络,其中 L Z 为 M 个负载阻抗, , g g Z v 1 分别为内部阻 抗和外部激励源开路电压。利 用 M 端口网络的基 尔霍夫定律[6,7],有如下公式: 1 111 11 11 11 jjMM sMS jjj jjMjMs jS M M jMjMMM sMS viZiZiZ iZ viZiZiZ iZ viZiZiZ iZ (7) 空式中 ij Z ij 表示天线 和之间的互阻抗,ij ii Z 为为端 的自阻抗,端口电流与负载有如下关系: i , 1,2,, j jL ivZj M (8) 若阵列模型中的所有单元均为开路,则有: 0, 1,2,, j ij M (9) 则(7)可以变为: 0 j j js s vv Zi (10) 将(9)和(10)代入(7 )得: T 000102 T 12 , ,,, ,,, oM M VZVV vvv Vvv v (11) 其中, 是天线端口的开路电压, 0 V Z 是归一化矩阵, 即 11 121 21 222 12 1 1 1 M LL L M LL L MM M LL ZZ Z ZZ Z ZZ Z ZZ Z Z ZZ Z ZZ Z M L (12) 则有: 1 0 VZV (13) 式中, Z 为互耦矩阵。上式变形为: 11 121 21 222 12 M M MM MM ZZZ ZZ Z Z ZZ Z (14) Copyright © 2013 Hanspub 14  阵列天线的互耦分析—基于感应电动势法的均匀圆阵互耦校正技术 从式(12)可以看出,要实现互耦情况下的 DOA 估 计,需要求出互耦矩阵。求解互耦系数的关键是求解 互阻抗,下面介绍互阻抗的求法。 2.3. 互阻抗的求法[8,9] 对于二元对称振子阵,假设二个阵元上都介入电 动势,于是在振子上激励起电流,在空间激发出电磁 场,二振子激发的电流和空间电磁场是相互作用和相 互制约的。这时振子的辐射阻抗不仅包括单个振子单 独存在于空间的自阻抗,而且包括感应辐射阻抗即受 另外一个振子感应出的电动势对应的阻抗,称为互阻 抗。互阻抗的求解可以用矩量法[10]也可以用感应电动 势法,下面介绍的是感应电动势法求解边靠边平行天 线的互阻抗,由于篇幅的限制,对简单的两根相距为 d,长度为 L的偶极子细天线,只给出具体互阻抗的 求解公式,如下: 22 21 22 30 2RCidCidL Cid LL L (15) 22 21 22 30 2 X Si dSidLL Sid LL (16) 21 122121 1212 Z ZRjXRjX (17) 其中 2Ln , 为奇数。其中n i Cx为余弦积分函 数,即: cos d x i Cxuu u i S ,为正弦积分 函数,即: x sin d x i Sxuu u, 为相位常数, L为天线的长度,d为两个天线之间的间距。 2.4. 校正的 DOA 估计算法 误差存在条件下,DOA 数学模型[11-13]为: , X tZA StNt (18) 式中,阵列流型 ,A 因误差而畸变为 ,ZA , 当阵列误差较大时,对于那些对阵列流型的精度比较 敏感的,将会产生很大的影响。阵列数据的协方差矩 阵为: 2 H HH REXtX tZAESSZAI 影响空间谱谱峰的尖锐程度,又会对谱峰的位置造成 影响。下面将以 MUSIC 算法为例,通过仿真实验来 说明阵元互耦误差对 DOA估计的影响。 3. 实验仿真 (19) 与幅相误差和阵元位置误差不同,阵元互耦误差既 仿真 1:假设阵列为由8阵元组成的均匀对称阵 振子 会 线阵,其中 1 ,每根天线的长度为 2L , 阵元间距 2d 。快拍数为 2000,输入信 20 dB,三个独号源为20 度,30度,50 度。图 1是 校正前(不考虑互耦)与校正后(考虑互耦)的MUSIC 谱 图,表 1为计算得到的互耦系数表。 仿真 2:假设阵列为由8阵元组成 噪比为 立信 的均匀对称阵 振子圆阵,其中 1 ,每根天线的长度为 2L , 圆阵的半径为 1 快拍数为 2000,输入 为 20dB,三个独立信号源为(20 度,50度),(50 度,80 度),(60 度,20度)。图 2是校正前(不考虑互耦)的 MUSIC 谱图,图 3是校正后(考虑互耦)的MUSIC 谱 图。 从 m。 信噪比 表1和表2可以看出:若为均匀线阵,则这里 的复对称矩阵 Z 具有 Toeplitz 特性。若为均匀圆阵, Z 具有复对称循环特性。且间距越大时,互耦系数 小。通过图1里校正前和校正后的空间谱对比以 越 Figure 1. Power spectra before and after calibration ofniform Tab l e 1 . r array u linear array 图1. 均匀线阵校正前与校正后的功率谱图 The mutual coefficient table of uniform linea 表1. 均匀线阵的互耦系数表 1,1 Z 1.0000 + 0.00i 001,5 Z −0.6 − 0.1187i 073 1,2 Z −0.2250 + 0.3080i 1,6 Z −0.0990 + 0.0558i 1,3 Z 0.1660 + 0.1858i 1,7 Z 0.0445 + 0.0846i 1,4 Z 0.1467 − 0.1045i 1,8 Z 0.0737~0.0369i Copyright © 2013 Hanspub 15 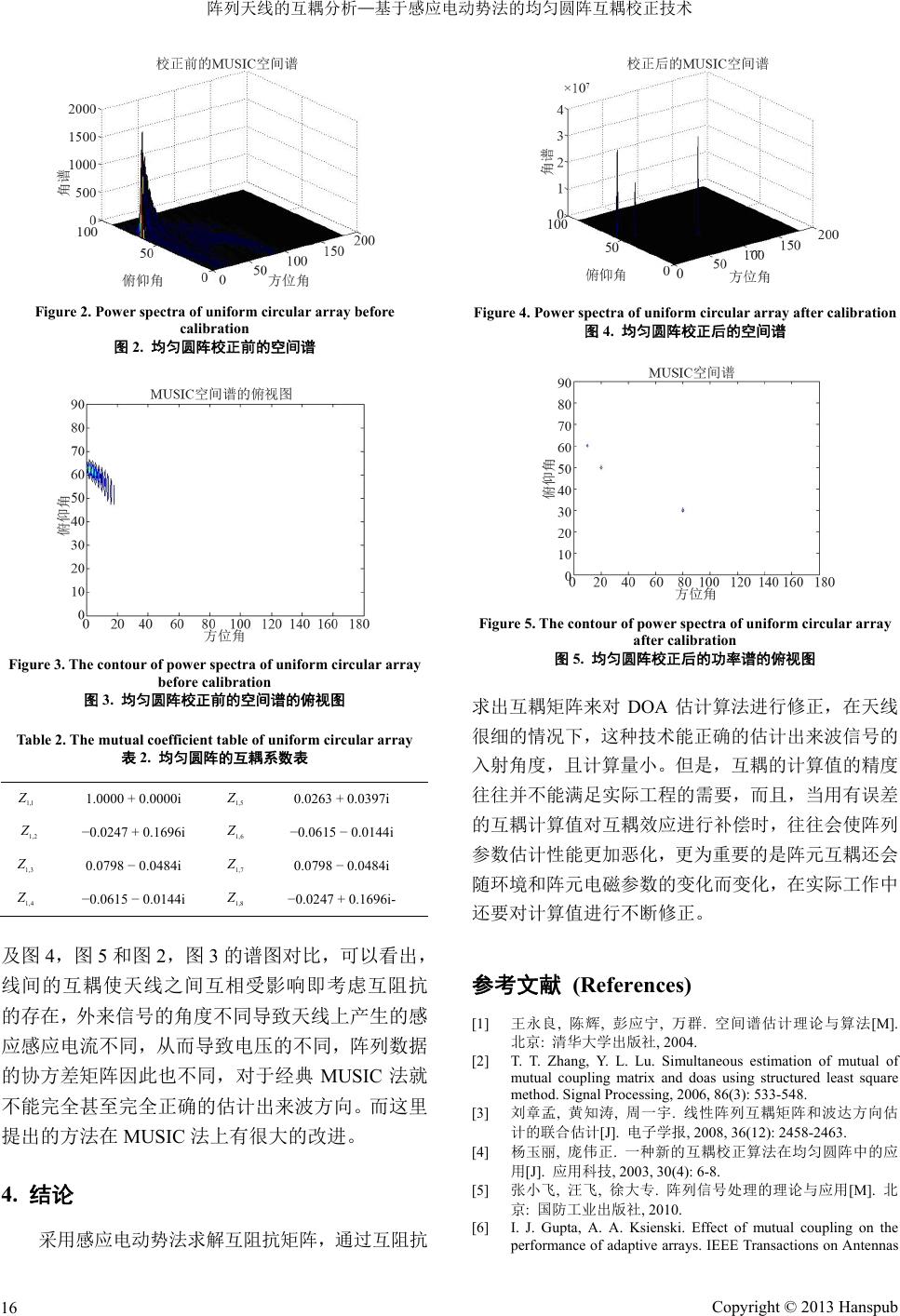 阵列天线的互耦分析—基于感应电动势法的均匀圆阵互耦校正技术 Figure 2. Power spectra of uniform circular array befe calibration or 图2. 均匀圆阵校正前的空间谱 Figure 3. The contour of power spectra of uniform circular array before calibration Table 2 . T array 表2. 均匀圆阵的互耦系数表 图3. 均匀圆阵校正前的空间谱的俯视图 he mutual coefficient table of uniform circular 1,1 Z 1.0000 + 0.0000i 1,5 Z 0.0263 + 0.0397i 1,2 Z −0.0247 + 0.1696i 1,6 Z −0.0615 − 0.0144i 1,3 Z 0.0798 − 0.0484i 1,7 Z 0.0798 − 0.0484i 1,4 Z −0.0615 − 0.0144i 1,8 Z −0.0247 + 0.1696i- 图4,图5和图 2,图 3的谱图对比,可以看出, 4. 结论 电动势法求解互阻抗矩阵,通过互阻抗 及 线间的互耦使天线之间互相受影响即考虑互阻抗 的存在,外来信号的角度不同导致天线上产生的感 应感应电流不同,从而导致电压的不同,阵列数据 的协方差矩阵因此也不同,对于经典 MUSIC 法就 不能完全甚至完全正确的估计出来波方向。而这里 提出的方法在 MUSIC 法上有很大的改进。 采用感应 Figure 4. Power spectra of uniform circular array after calibration 图4. 均匀圆阵校正后的空间谱 Figure 5. The contour of power spectra of uniform circular array 出互耦矩阵来对 DOA 估计算法进行修正,在天线 参考文献 (References) 空间谱估计理论与算法[M]. s. IEEE Transactions on Antennas after calibration 图5. 均匀圆阵校正后的功率谱的俯视图 求 很细的情况下,这种技术能正确的估计出来波信号的 入射角度,且计算量小。但是,互耦的计算值的精度 往往并不能满足实际工程的需要,而且,当用有误差 的互耦计算值对互耦效应进行补偿时,往往会使阵列 参数估计性能更加恶化,更为重要的是阵元互耦还会 随环境和阵元电磁参数的变化而变化,在实际工作中 还要对计算值进行不断修正。 [1] 王永良, 陈辉, 彭应宁, 万群. 北京: 清华大学出版社, 2004. [2] T. T. Zhang, Y. L. Lu. Simultaneous estimation of mutual of mutual coupling matrix and doas using structured least square method. Signal Processing, 2006, 86(3): 533-548. [3] 刘章孟, 黄知涛, 周一宇. 线性阵列互耦矩阵和波达方向估 计的联合估计[J] 电子学报, 2008, 36(12): 2458-. 2463. [4] 杨玉丽, 庞伟正. 一种新的互耦校正算法在均匀圆阵中的应 技): 6-8. 用[J]. 应用科, 2003, 30(4 [5] 张小飞, 汪飞, 徐大专. 阵列信号处理的理论与应用[M]. 北 : 国 版社, 2010. 京防工业出 [6] I. J. Gupta, A. A. Ksienski. Effect of mutual coupling on the performance of adaptive array Copyright © 2013 Hanspub 16  阵列天线的互耦分析—基于感应电动势法的均匀圆阵互耦校正技术 Copyright © 2013 Hanspub 17 tennas and Propagtion, 1988, 与信息学报, 2003, 7: 995-999. timations with the Presence of Mutual ual coupling compesation using subspace and Propagtion, 1983, 31(5): 1-7. [7] C.-C. Yeh, D. R. Ucci. Bearing estimation with mutual coupling present. IEEE Transactions on An 37(10): 1332-1335. [8] J. D. Kraus, R. J. Marhrfka. 天线[M]. 章文勋译. 北京: 电子 工业出版社, 2006. [9] 谢处方, 邱文杰. 天线原理与设计. 西安: 西北电讯工程学院 出版社, 1985 [10] 孙长果, 熊兵, 张晓丽, 张进民. 考虑互耦影响下的 DOA估 计算法[J]. 电子 [11] C. Yeh, M. Leou and D. R. Ucci. Bearing es mutual coupling present. IEEE Transactions on Antennas and Propagation, 1989, 37(10): 1332-1335. [12] Z. F. Ye, C. Liu. 2-D DOA Estimation in Coupling. IEEE Transactions on Antennas and Propagtion, 2008, 56(10): 3150-3158. [13] T. Svantesson. Mut fitting. Proceedings of IEEE Sensor Array and Multichannel Signal Processing Workshop, Cambridge, 2000: 494-498. |