 Open Journal of Transportation Technologies 交通技术, 2013, 2, 117-122 http://dx.doi.org/10.12677/ojtt.2013.22021 Published Online May 2013 (http://www.hanspub.org/journal/ojtt.html) Construction on the Immune Clonal Algorithm for Optimization Research of Emergency Material Scheduling* Linna Cheng, Deyuan Liu School of Traffic and Transportation, Lanzhou Jiaotong University, Lanzhou Email: chenglinnajiao@126.com Received: Jan. 18th, 2013; revised: Feb. 25th, 2013; accepted: Mar. 9 th, 2013 Copyright © 2013 Linna Cheng, Deyuan Liu. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. Abstract: Emergency material scheduling is one of the key links in order to improve the efficiency of the emergency rescue. Combining with the particularity of the emergency material and analyzing the influ ence of natural factors, accident character and base installation to selecting emergency supplies distribution plan, emergency supplies scheduling optimization model that is based upon more emergencies points and more kinds supplies is construc ted. In addition, this issue is solved by the immun e clonal algorithm. Taking emer- gency events of one region as an example, this paper analyzes the influence degree of every emergency points and every road segments. And by using Matlab software, an optimal distribution scheme of emergency supplies is proposed. The results show that the immune clonal algorithm can avoid form the premature con- vergence problem and is more efficient in optimization of multi-variab le function, moreover, it is an efficient method to resolve the problems of emergency supplies distribution. Keywords: Emergency Materials; Material Distribution; Objective Function Optimization; The Immune Clonal Algorithm 基于免疫克隆算法的应急物资调运优化研究* 成琳娜,刘德元 兰州交通大学交通运输学院,兰州 Email: chenglinnajiao@126.com 收稿日期:2013 年1月18 日;修回日期:2013 年2月25 日;录用日期:2013 年3月9日 摘 要:为了提高突发事件应急救援的效率,应急物资配送优化是应急救援的关键环节之一。本文结 合应急物资的特殊性,分析了自然因素、事故性质和基础设施对应急物资配送方案选择的影响,构造 出多应急点多种类物资条件下应急物资调运优化模型,并利用免疫克隆算法进行求解。最后,以某地 区应急事件为例,分析了各应急点及各路段的受影响程度,采用Matlab 计算平台,求解出最优的应急 物资配送方案。结果表明:免疫克隆算法可以避免早熟收敛现象,能够快速有效地收敛到最优解,是 求解应急物资配送问题的一种有效方法。 关键词:突发事件;应急物流;物资调运;免疫克隆算法 *基金项目:教育部人文社会科学研究规划基金(11YJCZH170);兰州市科技局研政产合作支撑计划项目(2011-1-111);甘肃省青年科技基金 (1208RJYA054)。 Copyright © 2013 Hanspub 117  基于免疫克隆算法的应急物资调运优化研究 Copyright © 2013 Hanspub 118 1. 引言 突发事件应急物资调运优化是一项复杂的系统 工程,受到物资种类、基础设施等多种因素的影响。 与传统的物资调运相比,应急物资调运有其自身的特 点,且该问题已被证明是一个NP-hard 问题,目前, 突发事件应急物资调运已成为政府和有关专家学者 们高度关注的热点和难点课题。为此,有关专家学者 们做了许多这方面的研究。文献[1]从组织结构和功能 体系两方面对应急物流系统进行了初步的设计,并构 造出单一条件下的应急物资调运模型;文献[2]建立了 应急资源静态单阶段调配优化模型,并对动态资源优 化问题进行了讨论;文献[3]同时考虑到物流应急中心 供给量、车辆载重和时间限制,利用启发式算法和遗 传算法相结合的方法对多出救点的应急物资调度问 题进行了研究;文献[4]以运输时间效益最大化为首要 目标建立模型,并转化成带有分层的网络流模型。 由于应急物资的特殊性,单从某一处应急点探讨 其调运方案的选择,难以满足实际应急需要。此外, 从多应急点的角度探讨应急物资的调运,存在多目 标、多种类物资等约束,使得该问题的求解非常复杂 [5]。大多既有研究主要探讨如何将应急物资快速有效 地从配送中心运往各应急点,而没有涉及多应急点和 多种类物资的全程调运问题。鉴于此,本文在既有相 关研究成果的基础上,综合考虑应急物资调运优化的 特殊性,将应急物流网络转化为带单边硬时间窗的作 业过程[6],以此建立多应急点和多种类物资共同约束 条件下的应急物资调运优化模型,为应急决策者提供 一定的理论依据。 2. 应急物资调运优化影响因素分析 1) 自然因素的影响。影响应急物资调运的自然因 素主要包括:应急物资自身的属性、应急地区的天气 气候状况、道路状况、应急事件发生的季节等。例如, 饮水、生活用品、药品等常用应急物资,就要依据它 们的不同特性来安排运送的先后次序,同时,灾害事 件也会造成不同程度的道路破损,影响应急物资的运 送,必须及时掌握运输途径的道路状况,选择最佳的 运输路线。 2) 应急事件性质的影响。应急事件的发生时间、 种类以及严重程度不同,对应急物资种类和数量的需 求就会不同,也就会影响到应急物资的调运。 3) 基础设施的影响。应急物资配送中心装卸设备 的数量、运送车辆的数量以及运输线路的数量都会影 响到应急物资的调运。 3. 应急物资调运优化数学模型的构建 3.1. 问题描述 假设 12 ,,, n A AA , m B 12 ,, kk CC 为n个应急物资配送中心, 为m个应急点,并设应急事件发生后需 要t种物资进行救援,第 k种物资在各配送中心的存 储量分别为 ,各应急点 对物资 k的需求量分别为 12 ,,BB , 1,2,, kn Ck t ,2,,t 12 ,, kk DD , 1 km D k,且配送中心的物资总 量大于等于应急点的总需求量。从配送中心 Ai到应急 点Bj运输物资 k所需的总时间记为 ,, m1, k ij Ti 2,,;1, 2nj ki E ki G ,物资 k在配送中心Ai 所需的装载时间为,物资 k在应急点 Bj所需的卸 载时间为。假设在不产生延误的情况下,物资 k 从配送中心Ai到应急点 Bj所需的运输时间为 k ij H ,单 位运输费用为 k ij F ,运送量为 k ij X 。 影响应急物资调运的随机因素有很多,当某些因 素的变化对应急物资调运产生影响时,就会出现应急 物资调运的延误现象,为此,本文定义物资 k在配送 中心 Ai到应急点 Bj的调运过程中,产生的延误时间为 ,延误系数为 。本文将应急物流网络转化为带 单边硬时间窗的作业过程,因此配送每种物资到应急 点都存在一个最大时间限制,将其与不产生任何延误 条件下的最小配送时间之差定义为机动时间 k ij Yk ij α k ij I ,并根 据不同因素对应急物资调运产生的不同程度的影响, 进行对比打分,确定出相对应的 ,本文将 定义 在0~1之间,进而求解出相对应的 ,即 k ij α k ij Y k ij ij α k k ij ij YI k 。 3.2. 约束条件分析 1) 配送中心的物资总量大于等于各应急点的总 需求量。考虑到多个地方会同时发生不同程度的应急 事件,各应急点所需的应急物资种类和数量也不尽相 同,为此,要满足每个应急点的需求。即 11 11 tn tm ki kj ki kj C D (1) 2) 每个配送中心对各种物资的配送量小于等于  基于免疫克隆算法的应急物资调运优化研究 存储量。各配送中心的物资存储量都是有限的,因此, 要寻求合理的分配方式,在允许条件下使得每个配送 中心的物资都能得到充分利用。即 11 1 1, 2,, nm n k ij ki ij i X Ck t (2) 3) 满足每个应急点对各种物资的需求量。在各种 物资存储量有限和多应急点条件下,通过合理分配每 种物资的供给量,使得各应急点都能得到及时有效的 救援。即 11 1 1, 2,, nm m k ij kj ij j X Dk t k (3) 4) 运送每种应急物资所需的总时间最小。影响应 急物资调运的各种因素会使物资调运产生不同程度 的延误,必须尽可能减少延误时间,用最短的时间将 物资及时送达应急点。即 kkkk ijijijij TEGHY (4) 5) 各种物资的运送量大于 0。 01,2, ,;1,2, ,;1,2, , k ij X injmk t (5) 3.3. 优化目标函数分析 应急物资的调运优化是一个多目标优化问题。考 虑到应急物流的弱经济性和紧急性,本文以配送时间 最小作为第一层目标,以较经济的运送方案作为第二 层目标,建立优化目标函数。 目标函数 1表示用最短的时间将所需物资从配送 中心运送到事故点: min max0 kk ij ij TTX (6) 目标函数 2表示在运送时间最短的基础上选择最 经济的运送方案: min max0 kkk ijij ij FFXX (7) 4. 免疫克隆算法设计与实现 4.1. 优化目标函数的处理 本文将免疫克隆算法应用于求解应急物资调运 的多目标优化问题,为了提高该算法的易操作性,首 问题。熵权法的具体步骤如下[7-9]: 先,利用信息熵将多目标规划问题转化为单目标规划 设有 b个待分析 方案 Step 1:数据矩阵归一化处理。 ,形成原始指标数据矩阵 2 cd b u U,根据式(6)、 (7)对其归一化,得到矩阵 R 2 cd b r。即 1 min b cdcd cd c ru u Step 2:计算第 c个因素下第 d个评价值的比重 和 cd p第c个因素的熵值 c e 11 ,ln b cdcdcd ccdcd cc prrefp p 若取 b 1lnfb ,则 01 c e 。 3:计算第 因素的差异系数Ste p c个c g 和权系数 cd w 1 1e,b cccdc c c g wg g 基于上述步骤,优化得到的单目标函数为: 12 min Z max0 max0 kkk kk ijijijij ij wT Xw FXX 4.2. 免疫克隆算法设计 4.2.1. 编码 的是多种类应急物资的调运优化,编码 时应 本文研究 对传统方法进行改进,即所构造的抗体是由 t段 子抗体(每段对应一种应急物资)构成的一个大抗体, 第k段子抗体表示应急物资k由哪几个配送中心运往 哪几个事故点。每段子抗体采用自然数编码,用 1, 2,, n 表示配送中心,用 1,2,,nnnm 表示应 时, nm 急点,此 个互不重 机排列 就构成了一个个 并对应一种物资调运方案。例如, 对于一个有 5个配送中心、3个应急点和 3种应急物 资的调运问题,则将 8个自然数(1~5 为配送中心,6~8 为应急点)随机排列产生的 3段 序列表示为应急物资 调运的方案,例如: 复的自然数的随 体, 11 22 33 12563748 23614758 34561278 第 段抗体(第 种应急物资) 第 段抗体(第 种应急物资) 第 段抗体(第 种应急物资) Copyright © 2013 Hanspub 11 9 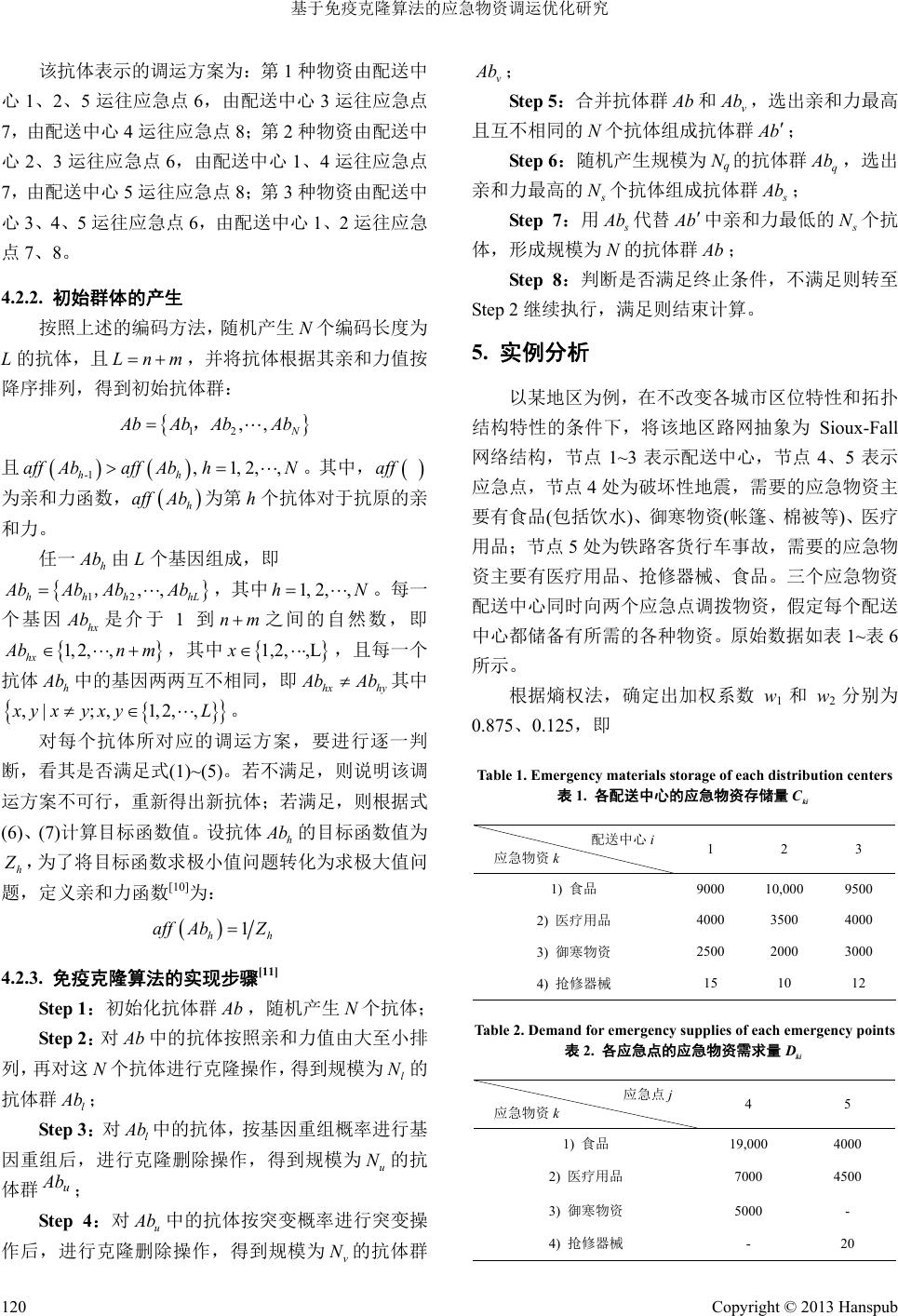 基于免疫克隆算法的应急物资调运优化研究 该抗体表示的调运方案为:第 1种物资由配送中 心1、2、5运往应急点 6,由配送中心 运往应急点 7,由配送中心 4运往应急点 8;第 2种物资由配送中 心2、3运往应急点 6,由配送中心 1、4运往应急点 7,由配送中心 5运往应急点 8;第 3种物资由配送中 心3 3 、4、5运往应急点 6,由配送中心 1、2运往应急 点7、8。 4.2.2. 初始群体的产生 按照上述的编码方法,随机产生 N个编码长度为 L的抗体,且 Lnm ,并将抗体根据其亲和力值按 降序排列,得到初始抗体群: 12 ,, N A bAbAb Ab, 且 aff Abaff Ab -1 ,1,2,, hh h N。其 中 , aff 为亲和力函数, h aff Ab为第 h个抗体对于抗原的亲 和力。 任一 h A b hh 由L个基因组成,即 L 12 ,, h h A bAAb Ab 因 b, hx ,其中 。每一1, ,,hN2 个基 A b是介于 1到nm 之间的自然数 1, 2,, hx ,即 A bn 中 1,2, ,Lx,且每一个 抗体 h m,其 A b中的基因两两互不相同,即 hx hy A bAb其中 | 1,2,, , ;, x yx yL。 调运方 逐一判 断,看其是否满足式(1)~(5) 不满足,则说明该调 得出新抗体;,则根据式 (6)、(7 算目标函数值。设抗体h yx 对每个抗体所对应的 案,要进行 。若 运方案不可行,重新 若满足 )计 A b的目标 值为函数 h Z ,为了将目标函数求极小值 化为求极大值问 题, 问题转 定义亲和力函数[10]为: 1 hh aff AbZ 4.2.3. 免疫克隆算法的实现步骤[11] Ste p 1:初始化抗体群 A b,随机产生 N个抗体; Step 2:对 A b 个抗体进 中的抗体按照亲和力值由大至小排 列,再对这N行克隆操作,得到规模为 的 抗体群 l N l A b; Step 3:对 l A b中的抗体,按基因重组概率进行基 因重组后,进行克隆删除操作,得到规模为 体群 u N的抗 Abu; Step 4:对u A b中的抗体按突变概率进行突变操 v 作后,进行 作,得到规模为 的抗体群 克隆删除操 v N A b; Step 5:合 体群并抗 A b和v A b,选出亲和力最高 且互不相同的 N个抗体组成抗体群 A b; St 6:ep 随机产生规模为 Nq的抗体群 q A b,选出 亲和力最高的 s N体组成抗体群个抗 s A b; Step 7:用 s A b代替 A b中亲和力最低的 s N个抗 体,形成规模为 的抗 N体群 A b; 条 5. 实例分析 例, 和 抽象为 Sioux-Fall 网络 的应急物资主 (包括饮水)、御寒物资(帐篷、棉被等)、医 疗 为铁路客货行车事故,需要的应急物 资主 配送中心 i k 1 2 3 Step 8:判断是否满足终止 件,不满足则转至 Step 2继续执行,满足则结束计算。 以某地区为在不改变各城市区位特性拓扑 结构特性的条件下,将该地区路网 结构,节点 1~3 表示配送中心,节点 4、5表示 应急点,节点 4处为破坏性地震,需要 要有食品 用品;节点 5处 要有医疗用品、抢修器械、食品。三个应急物资 配送中心同时向两个应急点调拨物资,假定每个配送 中心都储备有所需的各种物资。原始数据如表1~表6 所示。 根据熵权法,确定出加权系数 w1和w2分别为 0.875、0.125,即 Table 1. Emergency materials storage of each distribution centers 表1. 各配送中心的应急物资存储量 ki C 应急物资 1) 食品 9000 10,000 9500 2) 医疗用品 4000 3500 4000 4) 12 3) 御寒物资 2500 2000 3000 抢修器械 15 10 Table 2. Deforps of eachergency points 表2. 各应急点的应急物资需求量 应急点 j 应急物资 k 4 5 mand emergency suplie em ki D 1) 食品 19,000 4000 2) 医疗用品 7000 4500 4) 抢修器械 - 20 3) 御寒物资 5000 - Copyright © 2013 Hanspub 120 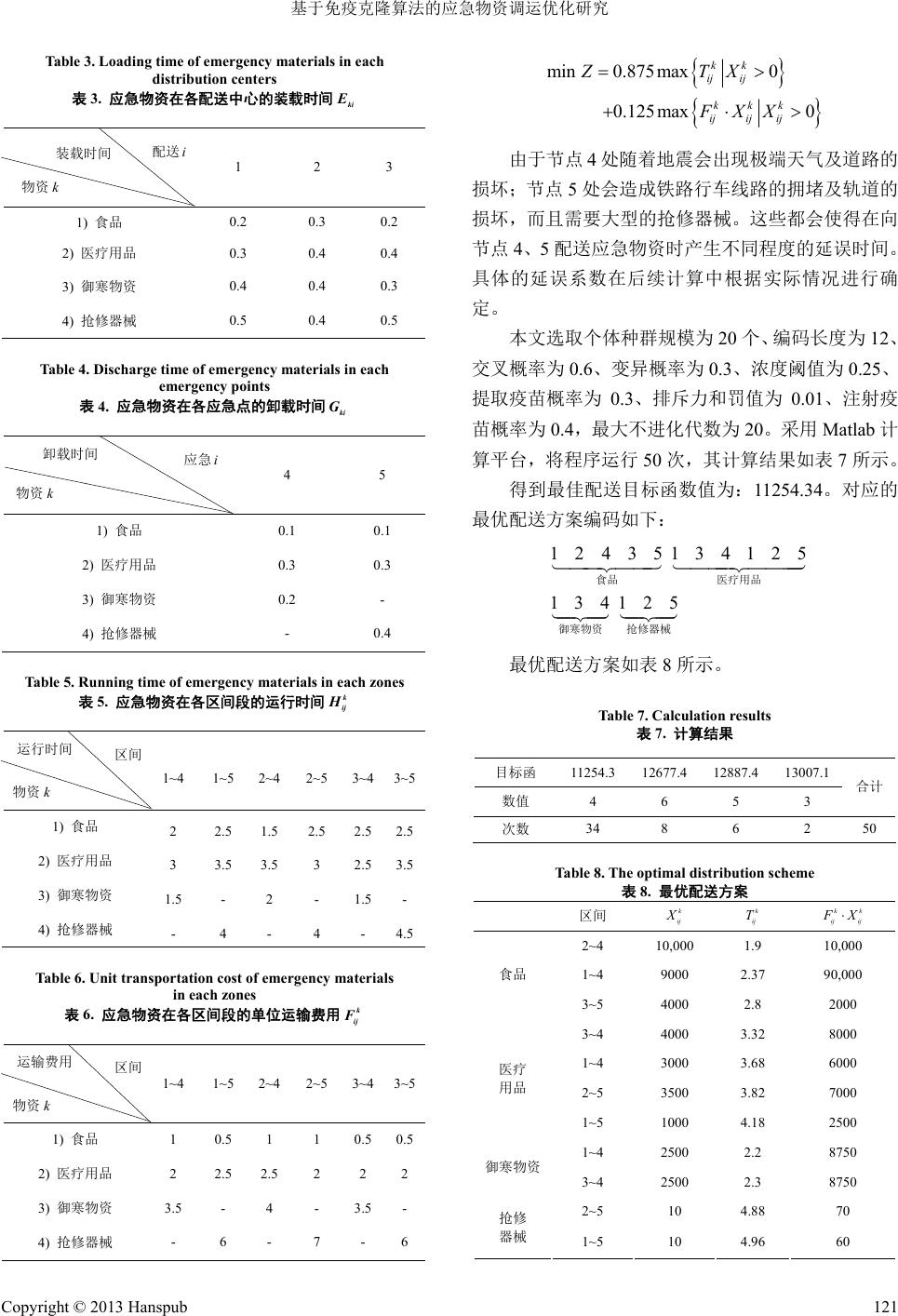 基于免疫克隆算法的应急物资调运优化研究 Table 3. Loadingergency materials in each center 表 应急物资在各配送中心的装载时间 time of em distributions 3. ki E 1 2 3 1) 食品 0.2 0.3 2 0. 2) 医疗用品 0.3 0.4 0.4 3) 0.3 4) 0.5 0.4 0.5 御寒物资 0.4 0.4 抢修器械 e 4. Di scharge time of emergency materials in each emergency points 急物资在各应急点的卸载时 4 5 Tabl 表4. 应间 Gki 1) 食品 0.1 0.1 2) 医疗用品0.3 0.3 3) 御寒物资 0.2 - - 0.4 4) 抢修器械 time of emergency materih zones 表资在各区间段的运 间 Table 5. Running als in eac k i 5. 应急物 行时 j H 2~4 2~5 3~43~51~4 1~5 1) 食品 2 2.5 1.5 2.5 2.52.5 2) 医疗用品 3 3.5 3.5 3 2.53.5 3) 御寒物资 1.5 - 2 - 1.5- - 4 - 4 - 4.5 4) 抢修器械 Taansportation cost of emergency materials nes 应急物资在 区间单 ble 6. Unit trin each 各 zo 段的表6. 位运输费用 k i j F 1~4 12 2~5 3~5~43~4~5 1) 食品 1 0.5 1 1 0.50.5 2) 医疗用品 5 2 2 2 3) 御寒物资 3.5 - 4 - 3.5- 4) 抢修器械 - 6 - 7 - 6 2 2.5 2. min 0. 0. 875max 0 125max 0 kk kk ijij ij ZTX FXX ij ij k 由于节点 4处随着地震现极端天气及道路的 损坏会造 铁路 车的拥堵道 损坏 大型修 械会在 节点应急物 时程度。 具体的延误系数在后续计算中根据实际情况进行确 定。 本文选取个体种群规模为 20个、编码长度为 12、 交叉 送方案编码如下: 会出 ;节点 5处成行线路及轨 的 ,而且需要的抢 器 。这些都 使得向 4、5配送资 产生不同的延误时间 概率为0.6、变异概率为 0.3、浓度阈值为 0.25、 提取疫苗概率为 0.3、排斥力和罚值为 0.01、注射疫 苗概率为 0.4,最大不进化代数为 20。采用 Matlab 计 算平台,将程序运行 50 次,其计算结果如表 7所示。 得到最佳配送目标函数值为:11254.34。对 应的 最优配 12435134125 1134 25 医疗用品 食品 抢修器械 御寒物资 最优配送方案如表 8所示。 算结果 目标函 11254.312677.4 12887.4 13007.1 Table 7. Calculation results 表7. 计 数值 4 6 5 3 合计 次数 34 8 6 2 50 tion scheme 区间 Table 8. The optimal distribu 表8. 最优配送方案 k ij X k T ij kk ij ij F X 2~10,000 4 1.9 10,000 1~4 9000 2.37 90,000 食品 3~5 4000 2.8 2000 3~4 4000 32 8000 1~4 3000 3.68 6000 7000 医疗 用品 00 4.2500 御寒物资 4. 抢修 器械 1~5 10 4.96 60 3. 2~5 3500 3.82 1~5 1018 1~4 2500 2.2 8750 3~4 2500 2.3 8750 2~5 10 88 70 配 时间 送i 装载 物资 k 应急 i 卸载时间 物资 k 运行时间 物资 k 区间 区间 运输费用 物资 k Copyright © 2013 Hanspub 121  基于免疫克隆算法的应急物资调运优化研究 Copyright © 2013 Hanspub 122 本文通过 急物资调运优化模型进 行了应用,同验证克隆 求解应急物 资配送问题方 有效疫克通过引入亲 合度成熟、克 记忆利 应的算子保证 快速地收敛到 最优且能地避免早熟 收敛现象,是应急送问 种快速有效 的方法。 6. 致谢 感谢一起学习工作的同学们,正是有了 支持,我才能克服一个个的困难,直至本 完成。 的物资调运模型研究[D]. 北京: 北京交通 [2] 王军. 铁路重大突发事件应急资源优化调配问题的研究[D]. 交通大学, 2002. [3] 王玲玲. 多出救点应急调度研究[J]. 铁道运输与经 济, 2010, 7(32): 47-52. 流运输问题优化研究[J]. 9-40. nd intake of radioactive material: ency 上述实例对应 时也 了免疫 算法在 面的 性。免隆算法 隆和等机理, 用相 全局 解,并够有效 求解 物资配 题的一 本论文在写作过程中遇到了很多的困难和障碍, 但都在老师和同学的帮助下度过了。尤其要强烈感谢 导师的亲切关怀和悉心指导,他严肃的科学态度,严 谨的治学精神,精益求精的工作作风,深深地感染和 激励着我,在此谨向导师致以诚挚的谢意和崇高的敬 意。我还要你 [1 们的帮助和 论文的顺利 最后,再次对关心、帮助我的老师和同学表示衷 心地感谢! 参考文献 (References) [1] 王杏. 救灾物流 中 大学, 2007. 北京: 北京 [4] 杜洁, 郝妍, 王璐. 多目标应急物 物理工程与管理, 2010, 4(32): 3 [5] 花明, 程蕾. 基于解释结构模型的应急物流影响因素研究[J]. 物流科技, 2009, 5: 117-119. 吴琳丽[6] 汪涛, . 基于粒子群算法的应急物资调度研究[J]. 军 事交通学院学报, 2011, 13(5): 70-74. 亮. 熵权[7] 郑晓薇, 樊华, 武亮 系数法的理论建模分析与并行 实现[J]. 小型微型计算机系统, 2007, 28(10): 1884-1887. B. G.uis. A[8] Lvoiding the closure of ports during a national emer- gency. IEEE International Conference on Technologies f or Home- land Security, 2011: 470-474. [9] V. Kutkov, E. Buqlova and T. McKenna. Severe deterministic effects of external exposure a Basis for emergency response criteria. Journal of Radiological Protection, 2011, 31(2): 237-253. 0] B. Fredrik, L. Jonas. Using live video for information sharing in emergency response work. International Journal of Emerg Management, 2009, 6(3-4): 295-301. [11] 马威. 基于免疫克隆算法的多目标 flow shop生产调度的研究 [D]. 上海: 华东理工大学, 2011. |